7.3: Division in other Bases

You will need: Base Blocks (Material Cards 3 - 15)

We will now work on dividing in other bases. First, we will divide by using repeated subtraction with the actual base blocks. Later, we'll employ the same algorithm we did in the previous exercise set to do the problems using repeated subtraction with the partial multiplication table, and the scaffold.

Get out your Base Three base blocks. We are going to use them with the repeated subtraction method to divide \(221_{\text{three}} \div 21_{\text{three}}\). The dividend is \(221_{\text{three}}\), which consists of 2 flats, 2 longs and 1 unit. We need to find out how many times we can repeatedly subtract the divisor, \(21_{\text{three}}\), from the dividend. To do this, we can convert the dividend into only longs and units by making some exchanges, and then form as many subsets containing 1 long and 2 units as possible. The number of subsets formed is how many times the divisor could be subtracted from the dividend. Get out your blocks to do this problem with me.

Step 1: Form the dividend in base three. You should actually get out your base three blocks and do the problems with the blocks. I will be using the initials for the base blocks (U, L, F, B, etc.) to show what is going on. The dividend can be shown like this:

F F L L U

Step 2: Make exchanges so it is possible to form as many subsets as possible, each containing the divisor, which is 2 longs and 1 unit. Each flat can be exchanged for 3 longs to get:

L L L L L L L L U

Then, one of the longs can be exchanged for 3 units to get L L L L L L L U U U U. Let's see if we can subtract out some equal subsets of 2 longs and 1 unit from the dividend. As you take out each 2 longs and a unit, form them in a subset.

I can take out and form 3 equal subsets of 2 longs and 1 unit each from the dividend. In the dividend, one long and 1 unit is left. The subsets formed look like this:

LLU

LLU

LLU

The part left in the dividend, which is the remainder looks like this:

LU

Step 3: Each equal subset of 2 longs and 1 unit that was subtracted out of the dividend counts as 1 for the quotient. Give yourself a unit for each equal subset you formed this is the quotient. The long and unit left over are the remainder because it is less than the divisor.

Quotient: U U U

Remainder: L U

Step 4: In the quotient and/or remainder, make any exchanges necessary so the quotient and remainder can be written in base three.

Quotient: L

Remainder: L U

Step 5: Write the quotient and remainder in base three: \(10_{\text{three}}r. 11_{\text{three}}\).

Therefore, \(221_{\text{three}} \div 21_{\text{three}} = 10_{\text{three}}r. 11_{\text{three}}\)

Step 6: Check the answer. This is shown to the right.

Exercise 1

Following the example on the previous page, do the following division step by step. Use base three blocks to do this exercise. You can either use initials, or draw pictures of the blocks to show how you do the division.

Do the following division: \(222_{\text{three}} \div 12_{\text{three}}\)

a. Form the dividend in base three. Draw a picture of what the dividend looks like:

b. Make exchanges so it is possible to form as many subsets as possible, each containing the divisor, which is 1 long and 2 units. Subtract out some equal subsets of 1 long and 2 units from the dividend. As you take out each long and 2 units, form them in a subset.Draw a picture of the all the equal subsets you were able to form by subtracting from the dividend, then draw a separate picture of what was left in the dividend, which will be the remainder (this must be less than 1 long and 2 units).

i) Show all of the equal subsets formed:

ii) Remainder:

c. For each of the equal subsets of 1 long and 2 units that was subtracted out of the dividend and formed (shown in b.i.), give yourself a unit — this is the quotient. Draw a picture of the quotient in terms of units:

d. In the quotient (part c) and/or remainder (part b.ii), make any exchanges necessary so the quotient and remainder can be written in base three. Draw a picture of what the quotient and remainder looks like after making any and all exchanges possible.

Quotient:

Remainder:

Check: \(\begin{aligned} 21_{\text{three}} \\ \underline{\times 10_{\text{three}}} \\ 210_{\text{three}} \\ \underline{+ 11_{\text{three}}} \\ 221_{\text{three}} \end{aligned}\)

e. Write the quotient and remainder in base three: ________________________

f. Check the answer.

Exercise 2

Use base blocks in the bases indicated to find the quotient and remainder for each problem. Then check your answer in the base given. Show your work. You can multiply using any multiplication algorithm you prefer — you might like to try the lattice.

a. \(1204_{\text{five}} \div 42_{\text{five}}\) = Check:	c. \(1345_{\text{six}} \div 25_{\text{six}}\) = Check:
b. \(323_{\text{four}} \div 23_{\text{four}}\) = Check:	d. \(11111_{\text{two}} \div 101_{\text{two}}\) = Check:

You may have noticed in parts c and d that you had to make a lot of piles, and that the repeated subtraction was somewhat tedious when you could only subtract one subset of divisor from the dividend at a time. This is where it is useful to use the idea that a long times the divisor is similar to multiplying by 10 in base ten. Remember that 10b is a long for some base, b. For instance, when you multiply 25 times 10, you get 250. In base six, \(25_{\text{six}}\) means 2 longs and 5 units. When you multiply this by a long (\(10_{\text{six}}\)), you get \(250_{\text{six}}\) which is 2 flats and 5 longs — every piece shifts up a place value. We can use this in exercise 2c to make the subtraction go faster. We'll do exercise 2c using this idea on the next page.

Exercise 2c, \(1345_{\text{six}} \div 25_{\text{six}}\), can be done using a more efficient method. Here are the steps:

Draw a picture of the dividend, \(1345_{\text{six}}\), using Base Six blocks.

B F F F L L L L U U U U U

You want to subtract as many subsets of the divisor, \(25_{\text{six}}\), from the dividend as you can. This would take a lot of steps. You'd have to break down the block and three flats into lots of longs and units. Now, \(25_{\text{six}}\), means 2 longs and 5 units. If you multiplied this by a long, you would have \(250_{\text{six}}\), which is 2 flats and 5 longs. If you subtracted 2 flats and 5 longs from the dividend at once, it would be the same as subtracting 2 longs and 5 units from the dividend six times! And it is possible to subtract 2 flats and 5 longs at once.

Let's trade some of the pieces in the dividend for smaller pieces, so it is possible to take subtract and make subsets of 2 flats and 5 longs. I started by trading the block in for 6 flats and two of the flats in for 12 longs:

F F F F F F F L L L L L L L L L L L L L L L L U U U U U

Now, I'll form as many subsets of 2 flats and 5 longs as possible.

F F L L L L L

F F L L L L L

F F L L L L L

I still have F L U U U U U left in the dividend, and can't take any more subsets of 2 flats and 5 longs out. So now, I try to subtract subsets of the divisor from what's left in the dividend. Again, I need to make some trades. I'll trade the flat for 5 longs and 6 units, so I have:

L L L L L L U U U U U U U U U U U

Two subsets can be formed:

L L U U U U U

L L U U U U U

All that is left in the dividend is a unit and 2 longs, which is less than the divisor, and is the remainder. So the remainder, LLU, is \(21_{\text{six}}\).

Now, we have to figure out the quotient. The first 3 subsets I formed were each a long times the divisor, so for the quotient, I put in a long for each of the subsets formed. I put in a unit for each of the next two subsets I formed. So I have 3 longs and 2 units for the quotient, and no exchanges need to be made.

The quotient is L L L U U, or \(32_{\text{six}}\), and the remainder is \(21_{\text{six}}\).

Therefore, \(1345_{\text{six}} \div 25_{\text{six}} = 32_{\text{six}}\)r. \(21_{\text{six}}\)

You should have gotten the same answer when you did exercise 2c, but you would have subtracted and formed 13 subsets of the divisor, and then traded 13 units in for the answer in base six.

(By the way, if the divisor, \(25_{\text{six}}\), was multiplied by a flat, you would have 2 blocks and 5 flats, which is bigger than the dividend, so we can't take that many of the divisor away at one time. So we start by subtracting subsets of a long times the divisor, one at a time.)

Exercise 3

Divide the following using base blocks. You can use the method described on the previous page, or subtract one subset of the divisor at a time. Explain or draw pictures with the blocks to show how you did the problem. Check your answers using any multiplication algorithm.

a. \(1046_{\text{seven}} \div 31_{\text{seven}}\) = _________________________________________________ Check:

b. \(10021_{\text{three}} \div 22_{\text{three}}\) = _________________________________________________ Check:

We're now going to work on doing division in different bases using the same repeated subtraction algorithm we did in Exercise Set 2. Since most if not all of us aren't familiar enough with different bases to estimate in our head, making up a partial multiplication table becomes extremely useful for these problems.

Because each base has a different number of digits, we may opt to do the doubling method or some partial table for larger bases like base 11, 12 and 13. For smaller bases, you might consider making a complete table. In base five, you would only have to figure out 2, 3 and 4 times the divisor (since 4 is the highest digit in base five). Study the following examples of using the scaffold method in other bases.

Example 1

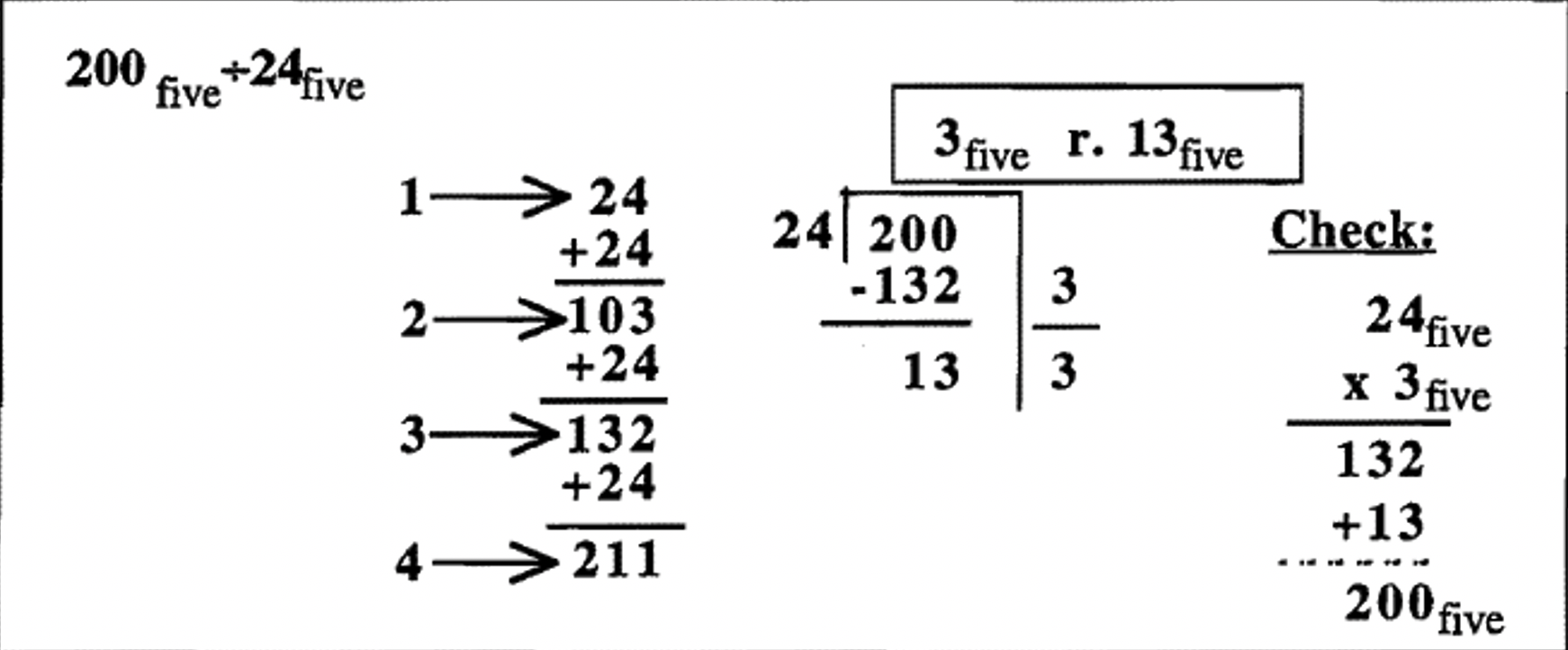
Division problem in base five: \(200_{\text{five}} \div 24_{\text{five}}\). I leave off writing "five" except for the answer (boxed) and the check. You have to be very careful to remember you are in base five when you are adding (the prep work at the beginning, and the addition at the end of the check when you add the remainder), subtracting (doing the repeated subtraction), and multiplying (in the check). For the check, you could use the lattice method, or any other method you prefer.

Example 2

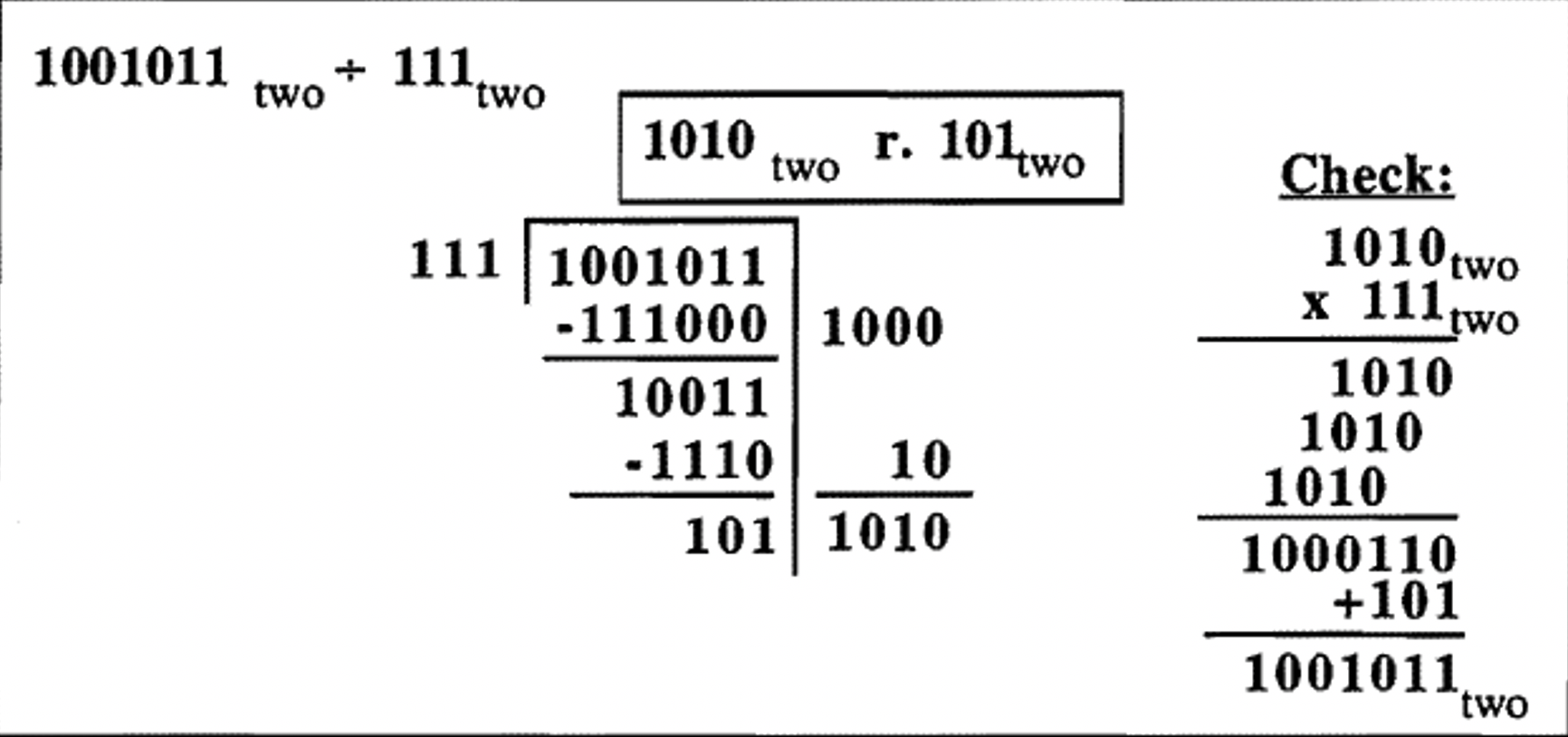
Division problem in base two: \(1001011_{\text{two}} \div 111_{\text{two}}\). There is really no prep work here, because the only digits in base two are 0 and 1.

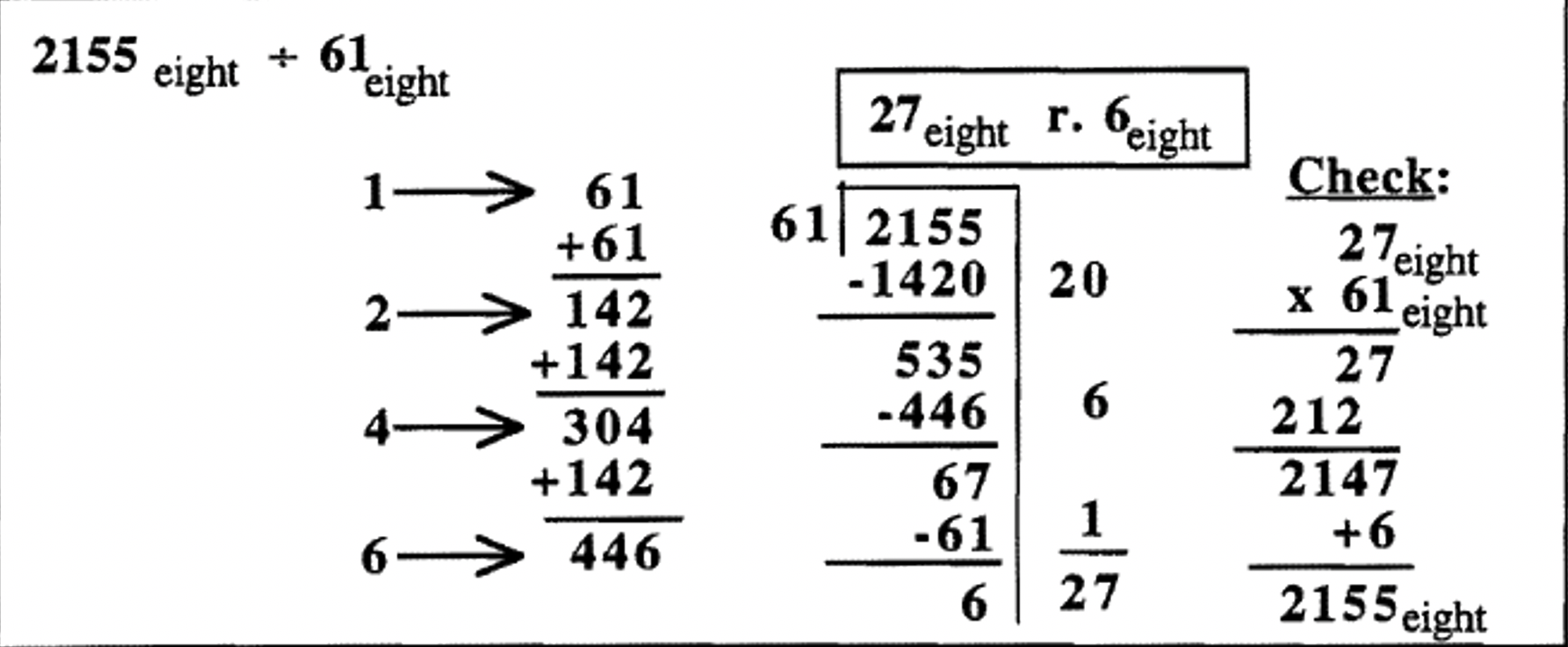
For examples 3 and 4, I chose to do a different kind of partial multiplication table for each.

Example 3

Division problem in base eight: \(2155_{\text{eight}} \div 61_{\text{eight}}\). Since this is a problem in base eight, I decided to make a partial table to figure out the divisor times 1, 2, 4, and 6. Another person might choose to do a table for only 1, 2, and 4. Remember that 7 is the highest digit in base eight. Yet another student might do a full table for all of the digits in base eight: 1, 2, 3, 4, 5, 6, and 7.

Example 4

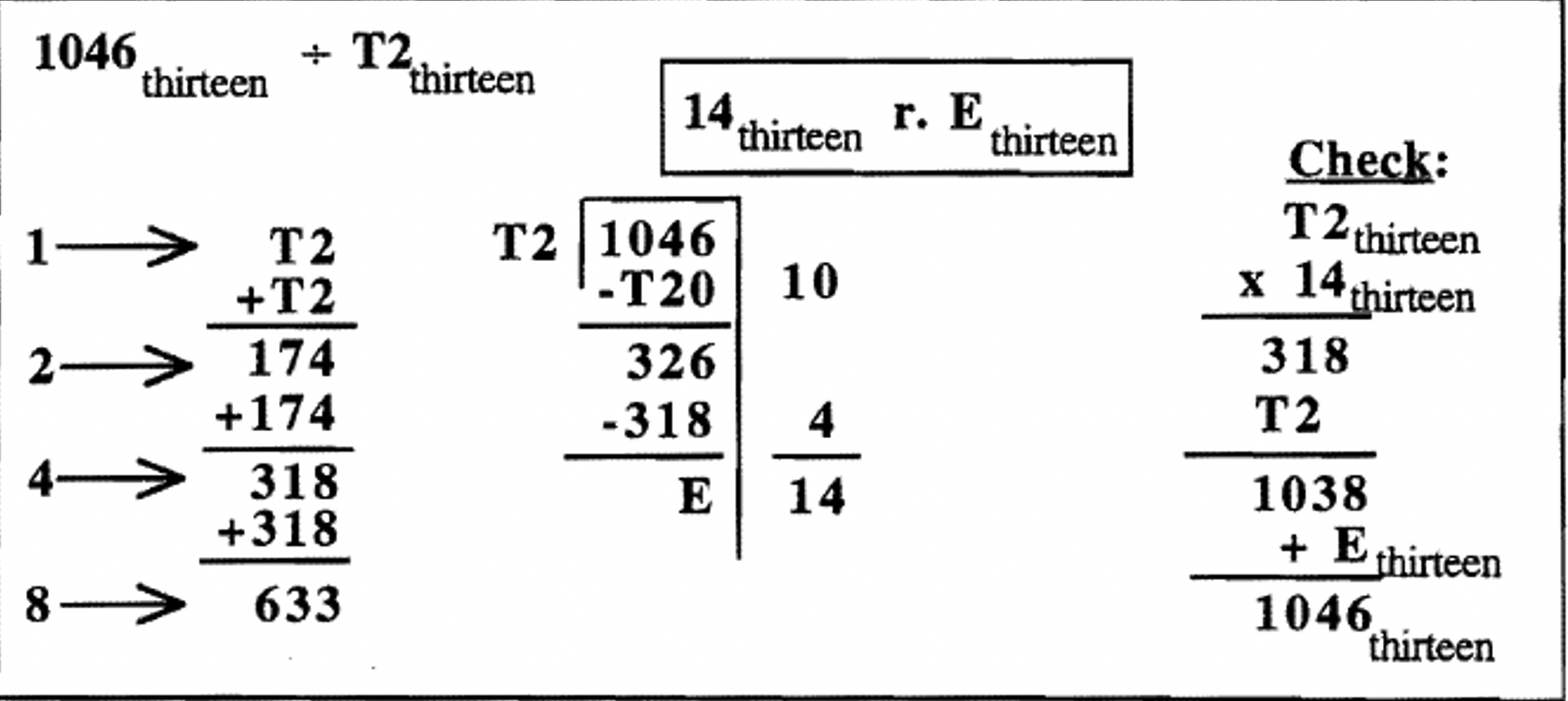
Division problem in base thirteen: \(1046_{\text{thirteen}} \div T2_{\text{thirteen}}\). Since this is a problem in base thirteen, I decided to make a partial table to figure out the divisor times 1, 2, 4, and 8. Remember that W is the highest digit in base eight. Another person might choose to do a table for 1, 2, 4, 6, 8, T, and W. Remember that W is the highest digit in base thirteen. Another student might make a full table for all of the digits in base thirteen, but that's a lot of prep work that usually doesn't pay off.

Make sure you practice the previous four examples before doing the exercises that follow on the next pages.

For each of the division problems in the remainder of this section, show your work, using a model similar to the last four examples. First make up a partial or full multiplication table (prep for division using repeated subtraction). Then, divide using the scaffold method with the repeated subtraction method. Write your answer in a box above the scaffold. Then, check your answer by multiplying the divisor by the quotient and adding the remainder. Make sure you pay close attention to what base you are working in as you add, subtract and/or multiply in that base. Remember to write the base when you write the quotient and remainder.

Exercise 4

\(222_{\text{three}} \div 12_{\text{three}}\)

Exercise 5

\(1204_{\text{five}} \div 42_{\text{five}}\)

Exercise 6

\(323_{\text{four}} \div 23_{\text{four}}\)

Exercise 7

\(1345_{\text{six}} \div 25_{\text{six}}\)

Exercise 8

\(11111_{\text{two}} \div 101_{\text{two}}\)

Exercise 9

\(1046_{\text{seven}} \div 31_{\text{seven}}\)

Exercise 10

\(10021_{\text{three}} \div 22_{\text{three}}\)

Exercise 11

\(200_{\text{five}} \div 3_{\text{five}}\)

Exercise 12

\(1001011_{\text{two}} \div 1010_{\text{two}}\)

Exercise 13

\(2155_{\text{eight}} \div 27_{\text{eight}}\)

Exercise 14

\(1046_{\text{thirteen}} \div 14_{\text{thirteen}}\)

Exercise 15

\(101\text{E}_{\text{twelve}} \div 54_{\text{twelve}}\)