7.2: Division Algorithms

As we've seen, division can be viewed as the opposite of multiplication.

Another way to think about it is as REPEATED SUBTRACTION.

Let's do DIVISION the Easy Way!

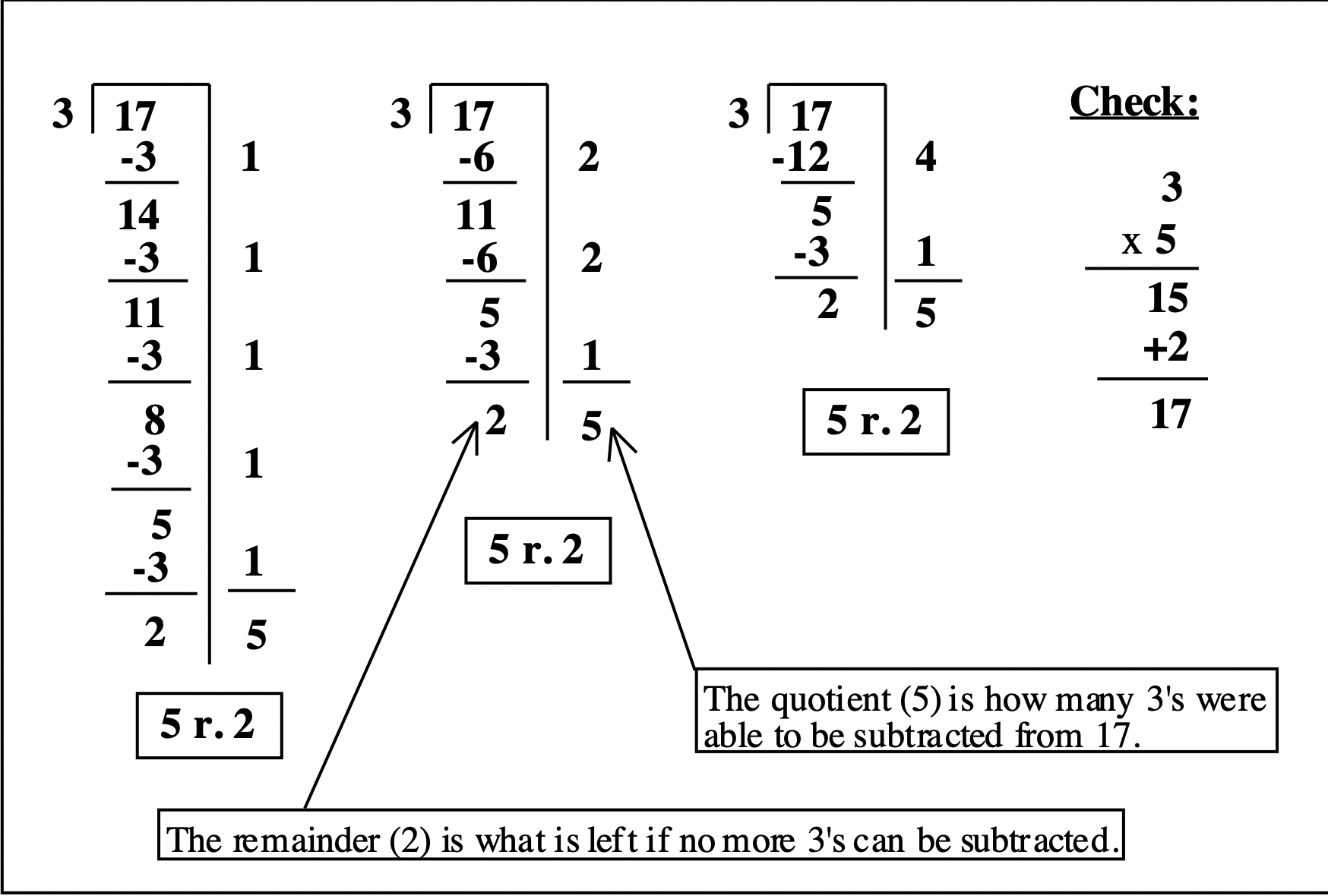
That's right. Division is really just "repeated subtraction." If you are asked to divide 17 by 3, which is written \(17 \div 3\), you have to figure out how many 3's can be subtracted from 17. You probably already know the answer is 5 r. 2, but let's see how this works by counting how many times 3 can be subtracted from 17. Look at the work below. Three different ways are shown. You make a scaffold (looks like a hangman) and keep track of how many 3's you subtract at each step to the right of the scaffold. In the first one, 3 is subtracted one at a time, and a total of five 3's were subtracted. In the second one, first two 3's are subtracted, then 1 more, then 2 more, for a total of five 3's being subtracted. In the third one, four 3's are subtracted, and then 1 more, again for a total of five 3's being subtracted. Each time you subtract, look to see what number is left. If it is 3 or more, you can subtract some more 3's. But when you get a number smaller than 3, you know 3 can't be subtracted anymore, so that is your remainder. For this problem, 2 was the remainder. You need to count how many 3's you subtracted. To the right of the scaffold, you write how many 3's you are subtracting as you go along. Simply add those numbers to find out how many 3's you subtracted. The answer to the problem is how many 3's you subtracted, and then you need to also write the remainder. In this case, \(17 \div 3 = 5\) r. 2. Always check your answer my multiplying the divisor (3) times the quotient (5) and adding the remainder (2): \(3 \times 5 + 2 = 15 + 2 = 17\). It checks!

Doing long division with large numbers is often difficult because you have to multiply in your head, and it's easy to make mistakes. But, by using this new method of repeated subtraction, along with a partial multiplication you make up ahead of time using repeated addition, you never have to multiply in your head (or multiply at all), and you never have to guess how many times one number "goes into" another number. This method takes a little more paper, but it makes the problem easier and it's practically foolproof. Lots of people don't like to do long division, because it's hard to always guess the exact right number and sometimes they get a headache from thinking too hard. We're going to eliminate that problem. The important thing is that you know what division means (repeated subtraction), you know how to get the right answer using a method that makes sense to you, and you know how to check your answer to make sure it is right.

Okay, so let's say you had to do this division problem: \(361 \div 53\).

YUK! This doesn't look like any fun. Actually, all this is asking is how many 53's can be subtracted from 361. We can subtract 53 one at a time, but it might take a long time. We might decide to subtract more than one 53 at a time.

Before we doing the division, let's make a quick partial multiplication table up for 53, by using REPEATED ADDITION! This table is your prep work for division. A simple way to make up a partial multiplication table for 53 without ever multiplying entails doubling numbers. We know that \(1 \times 53 = 53\). To figure out \(2 \times 53\), just add two 53's together. Two 53's added to two more 53's would equal four 53's, or \(4 \times 53\). Four 53's added to four more 53's would equal eight 53's, or \(8 \times 53\). Okay, so how do you show this? Start with one 53 and double it to find two 53's. Double that number to find four 53's. Double that number to find eight 53's. Look in the left part of the box shown below. See how there is a 1 pointing to 53 that means \(1 \times 53\). If you double the 53, (53 + 53), then you now know \(2 \times 53 = 106\), so a 2 points to 106. If you double that (106 + 106), you now know \(4 \times 53 = 212\), so a 4 points to 212. And if you double this number (212 + 212), then you now know \(8 \times 53 = 424\), so an 8 points to 424. Isn't that an easy way to find \(8 \times 53\)? But the cool thing is that you also know \(1 \times 53, 2 \times 53, 4 \times 53,\) AND \(8 \times 53\)! This is useful to know to do the long division. Instead of guessing how many times 53 "goes into" 361, we note how many 53's can be subtracted from 361 (underestimating is okay). No multiplication needs to be done in your head, either! The box to the right shows how to use repeated subtraction to do the division problem: \(361 \div 53\). First, make up a partial multiplication table. Then, write the division problem using a scaffold. Look at the multiplication table and pick the biggest number you can subtract from 361, which is 212. Subtract 212 from 361 and write 4 on the right because you just subtracted 4 53's. The biggest number you can subtract from 149 is 106. If you do that, you've subtracted 2 more 53's, so write a 2 on the right. After subtracting, 43 is left and no more 53's can be subtracted. Therefore, 43 is the remainder. Add the numbers on the right to see how many 53's you subtracted. The answer is 6 r. 43. To check, multiply \(53 \times 6\) and add 43. The answer is 361.

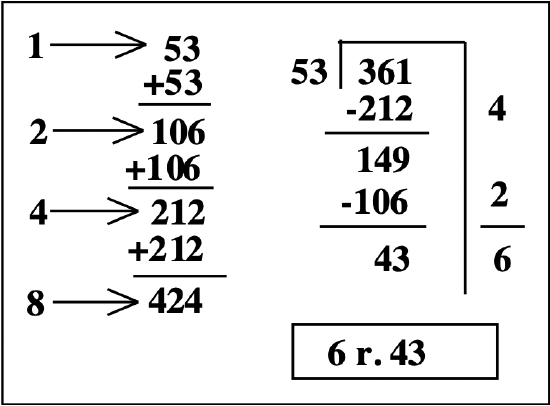
P.S. You can multiply 53 times 6 by adding 106 + 106 + 106, since that is two 53's added together 3 times, which is six 53's!!!

Here are some more examples for you to study. A partial multiplication table is made up first. This prep work which involves a few additions makes the division much easier. Then, the problem is done using repeated subtraction (with help from the partial multiplication table) using a scaffold. After adding up how many times the divisor was subtracted from the dividend (the numbers to the right of the scaffold), the answer (quotient and remainder) is written in a box up above the problem. Finally, the check is shown. Also, check to make sure the remainder is less than the divisor.

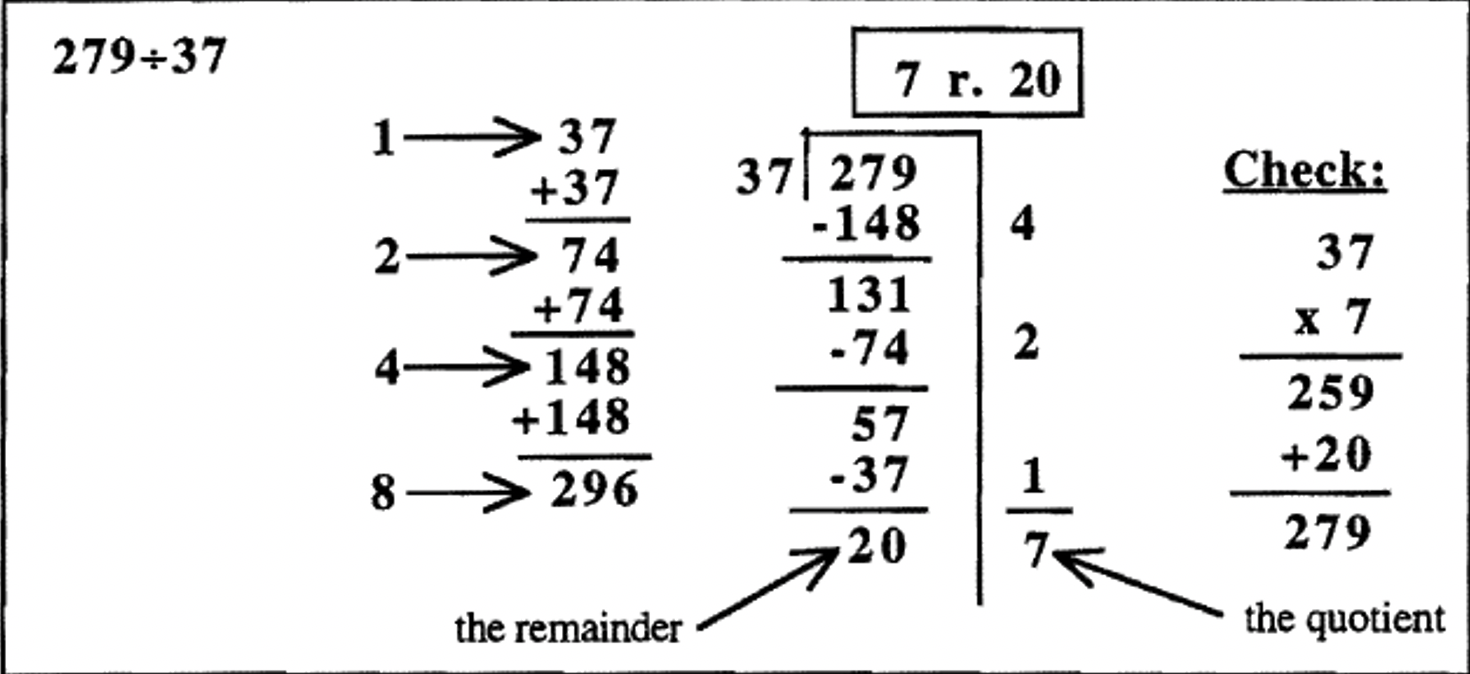
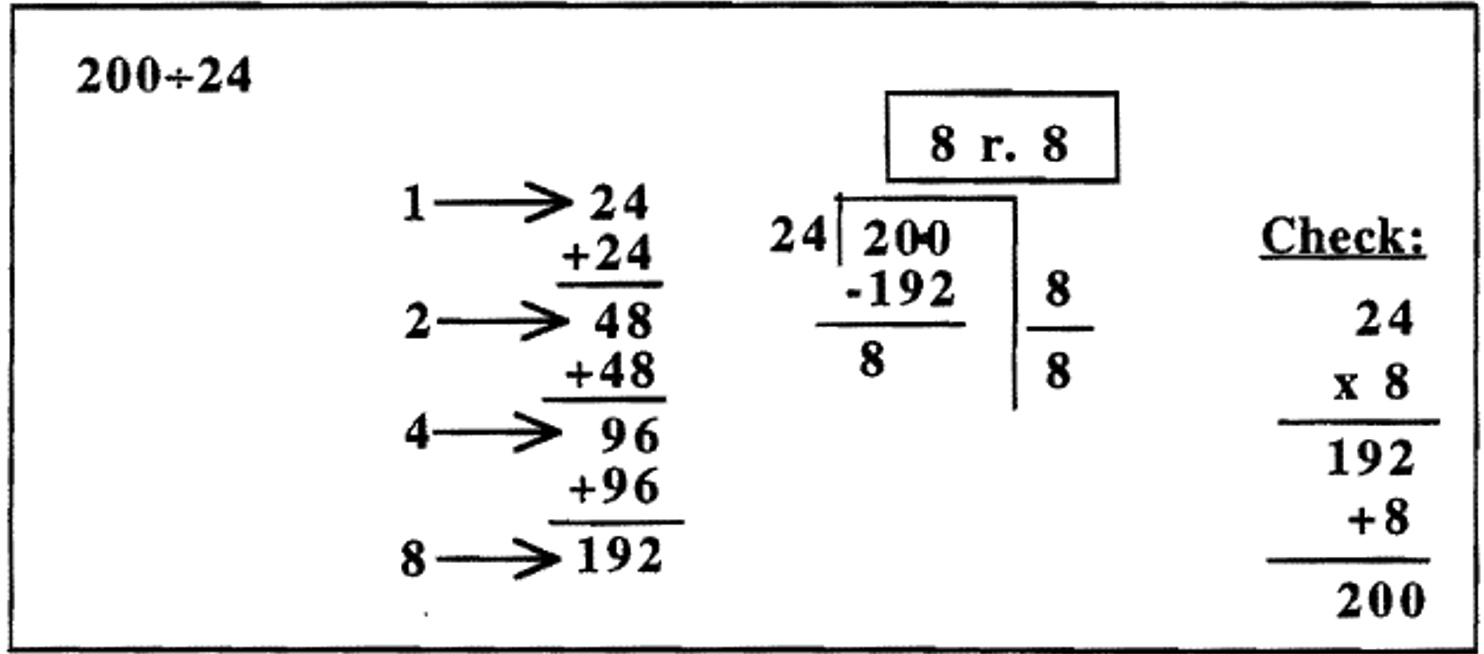
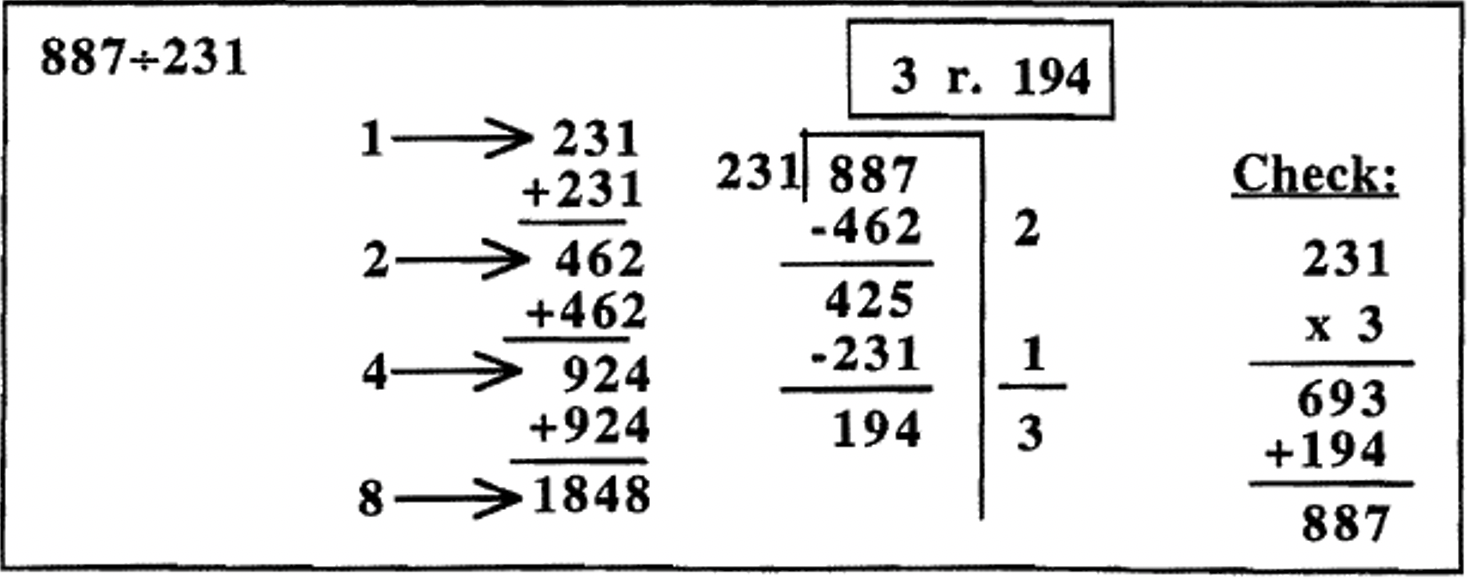
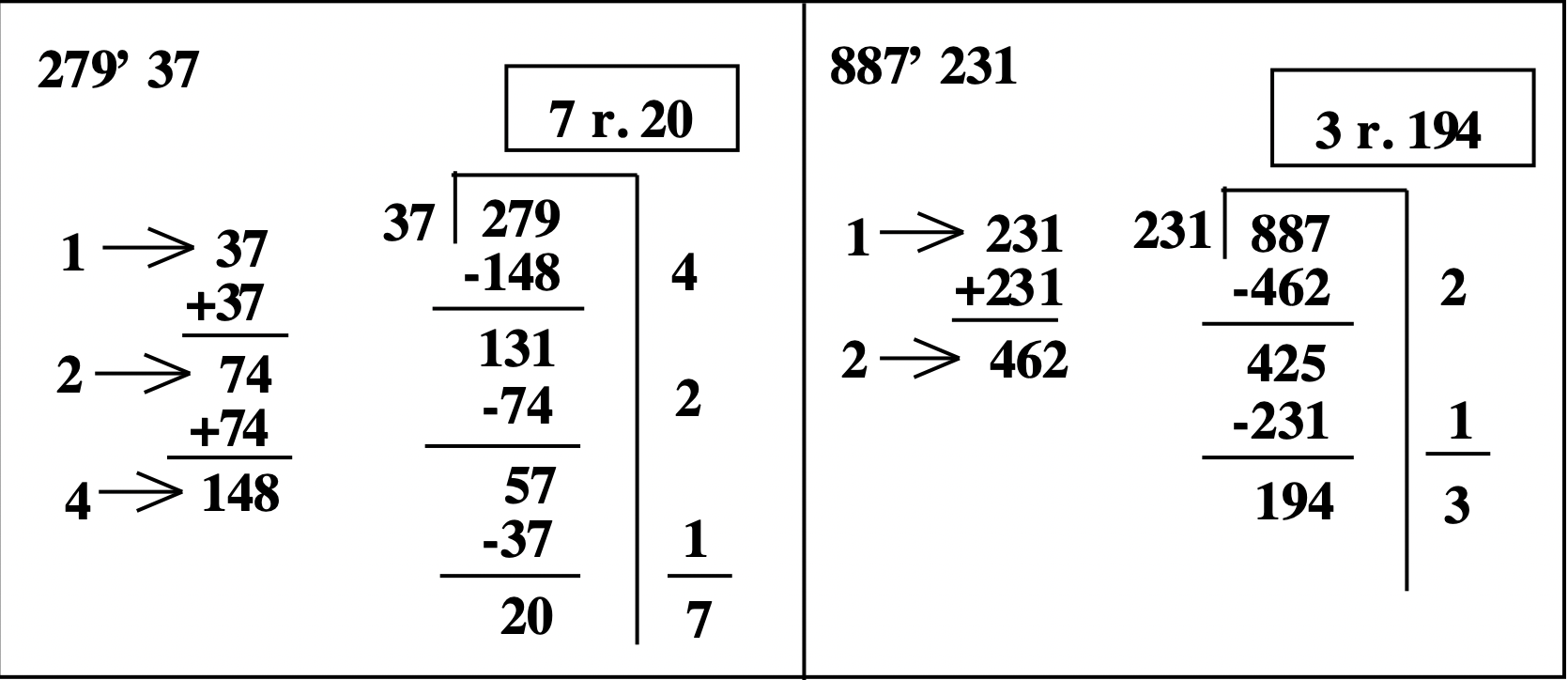
In the examples so far, all of the quotients were less than 10. It's possible to continue doubling the divisor in the partial multiplication table, so that you can find the divisor times any power of 2 — 1, 2, 4, 8, 16, 32, 64, etc. You would stop doubling if you notice that doubling once more gives a number bigger than the quotient. In fact, in the first example on the previous page, \(279 \div 37\), I really didn't have to double 148 to figure out \(8 \times 37\), since doubling 148 gives me a number bigger than 279. In the third example, \(887 \div 231\), I didn't have to double 462 to figure out \(4 \times 231\), since doubling 462 gives a number bigger than 887. The problems could have been shortened slightly had I noticed that ahead of time. They would look like this (the check is omitted).

Okay, now that you've studied some examples, it's time for you to try using this method. The first four problems are the same exact ones done in the previous examples. If you get stuck, look back at them and copy how I did them on another piece of paper. Then, try again.

Exercise 1

For each division problem, do your prep work by using the doubling method (double as far as necessary) to make a partial multiplication table first. Then, draw a scaffold, and use repeated subtraction to do each division. When you are done, make sure the remainder is less than the divisor. Then, check the answer. All work should be shown in the space provided. After checking, write the answer on the space provided at the beginning of the problem.

a. \(361 \div 53\) = _______________ Partial multiplication table: Scaffold: Check:

b. \(279 \div 37\) = _______________ Partial multiplication table: Scaffold: Check:

c. \(200 \div 24\) = ___________________ Partial multiplication table: Scaffold: Check:

d. \(887 \div 231\) = ______________ Partial multiplication table: Scaffold: Check:

e. \(415 \div 72\) = _______________ Partial multiplication table: Scaffold: Check:

f. \(1235 \div 214\) = _____________ Partial multiplication table: Scaffold: Check:

g. \(3128 \div 321\) = _____________ Partial multiplication table: Scaffold: Check:

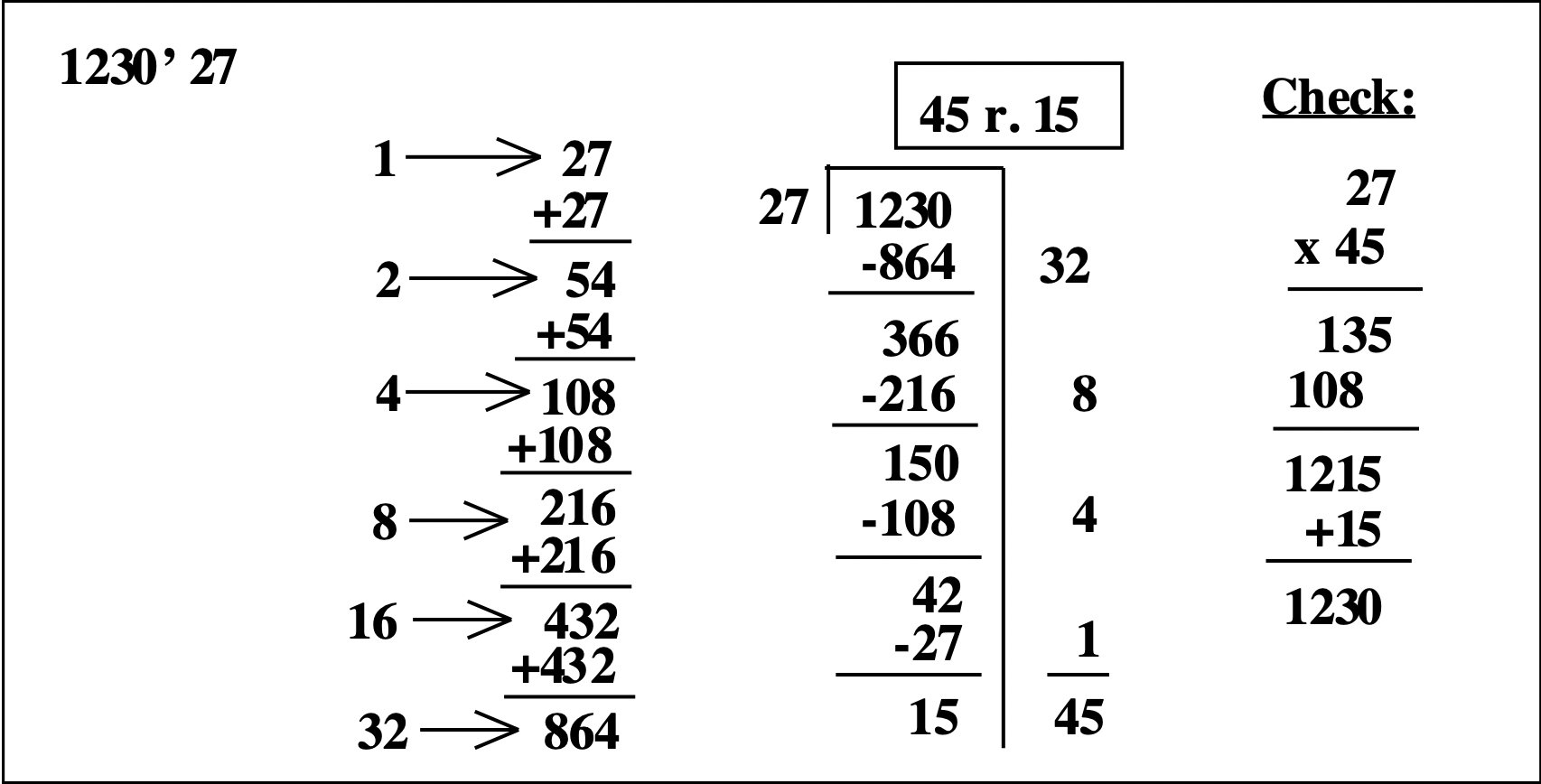
The following is an example to show that the doubling can continue in this way. You stop doubling if one more double gives a number bigger than the quotient. Below is \(1230 \div 27\).

I thank and credit my son, Jakob, with this method of doubling to figure out more than eight times the divisor. I had always used a method that employed the use of place values and multiples of 10, which we'll get to after doing a few this way. Jakob, nine years old and in fourth grade, hated long division because it didn't make sense to him, and had trouble with the "guessing" involved. Before I was able to show him my method where you use the doubling method to make a partial multiplication table only up to 8 times the divisor, he did all of the problems like the way shown above. It finally made sense to him, and he did them all correctly!!! It opened up a whole new way of thinking for me. Kids and students can be great innovators! It's wonderful when you get a chance to explore and discover on your own, and find your own solution that makes sense. We have to remember that there is nothing sacred about any one algorithm for division, or any other operation.

Okay, it's time for you to try some more problems, using the doubling method, where the quotient is bigger than 10. The first problem is the same exact one done above. If you get stuck, look back at it and copy how I did it on another piece of paper. Then, try again.

Exercise 2

For each division problem (starting on the next page), use the doubling method (double as far as necessary) to make a partial multiplication table. Then, draw a scaffold, and use repeated subtraction to do each division. Then, check the answer, and make sure the remainder is less than the dividend. All work should be shown. After checking, write the answer on the space provided at the beginning of the problem.

Check: \(\begin{aligned} 27 \\ \underline{\times 45} \\ 1215 \\ \underline{+ 15} \\ 1230 \end{aligned}\)

A calculator may be used to check the answer. For instance, to check that 45 r. 15 is the correct answer to \(1230 \div 27\), you need to multiply 27 by 45 and add 15. The answer should be 1230. You can use the calculator to do the multiplication and addition, but write down the steps.. It would look the way it is shown to the right.

a. \(1230 \div 27\) = ______________ Partial multiplication table: Scaffold: Check:

b. \(603 \div 48\) = _______________ Partial multiplication table: Scaffold: Check:

c. \(1346 \div 41\) = ______________ Partial multiplication table: Scaffold: Check:

d. \(3512 \div 43\) = ______________ Partial multiplication table: Scaffold: Check:

You may have noticed the partial multiplication table could get long if you have to keep doubling for quite awhile. Also, it's not as easy to add the numbers up to the right of the scaffold. Another approach is to take advantage of the fact that multiplying a whole number by 10 or 100, etc., simply adds zeroes to the end of the number. For instance, if you know 53 times 2 is 106, then 53 times 20 is 1060, and 53 times 200 is 10600. We'll use this fact to divide using repeated subtraction when the quotient is more than 10.

Look back at the last problem you did in Exercise 2: \(3512 \div 43\). You had to double until you figured out what 64 times 43 was. In the box at the bottom of this page is a different way of doing the same problem. The explanation and steps are on this and the next page.

Step 1: Use doubling to make up a partial multiplication table up to 8 times 43.

Step 2: Draw the scaffold.

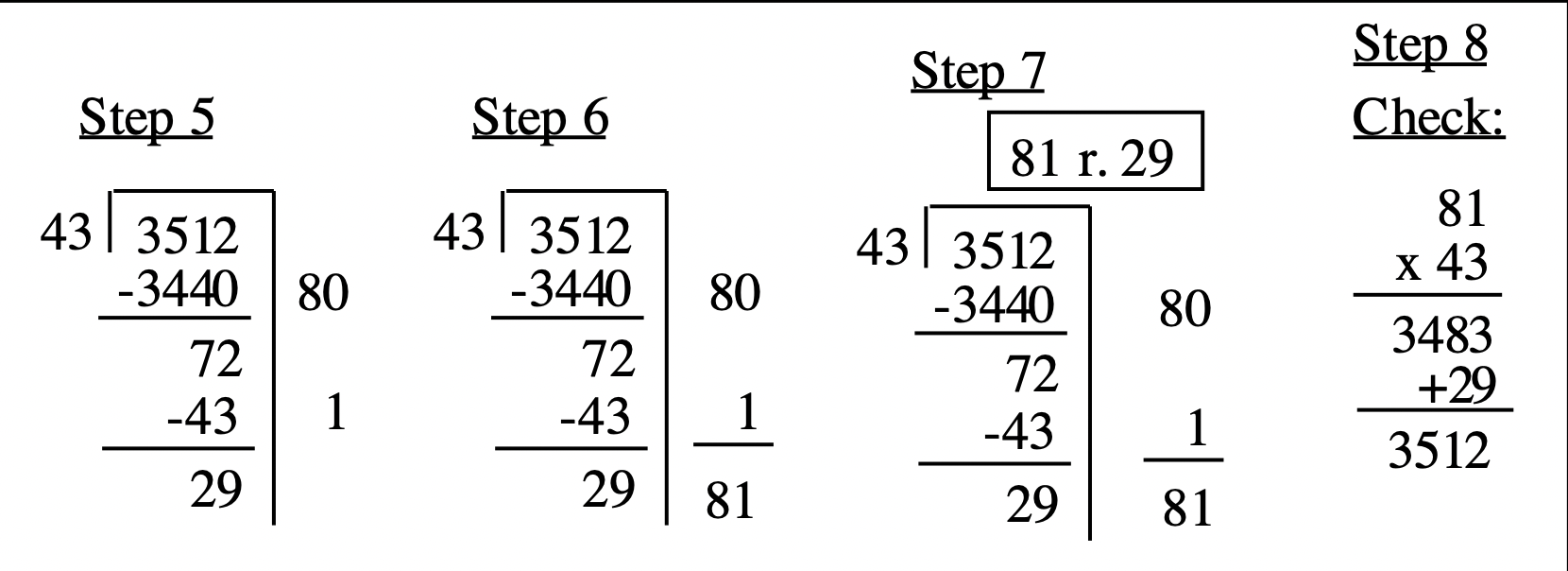
Step 3: Scan 3512 starting with the left-most digit until you get a number greater or equal to 43. Try 3, then 35, then 351. Note how many more digits are after 351. In this case there is only one (the 2). This means you can take a multiple of ten times 43 away at a time. (In the old standard algorithm, when you guess and put the number above the 1 in 3512, you are putting it in the tens place value.) So we put a zero under the extra numbers in the dividend (the 2) and the same number of zeroes to the right of the scaffold. Leave a space for a digit before the 0 on the right of the scaffold.

Step 4: Now, look at the partial multiplication table to determine the largest number you can subtract from 351. It is 344, which is 8 times 43. Note that if 8 times 43 is 344, then 80 times 43 is 3440. You've already put the extra zero under the 2, so just put the 344 in front of the 0 that you already put down in step 3. Note that 3440 is 80 times 43, and you need to keep track of that to the right of the scaffold. You've already written the zero down in step 3, so simply put an 8 in front of that 0. You've just subtracted eighty 43's from the dividend, since 80 times 43 is 3440. Subtract 3440 from 3512 to get 72.

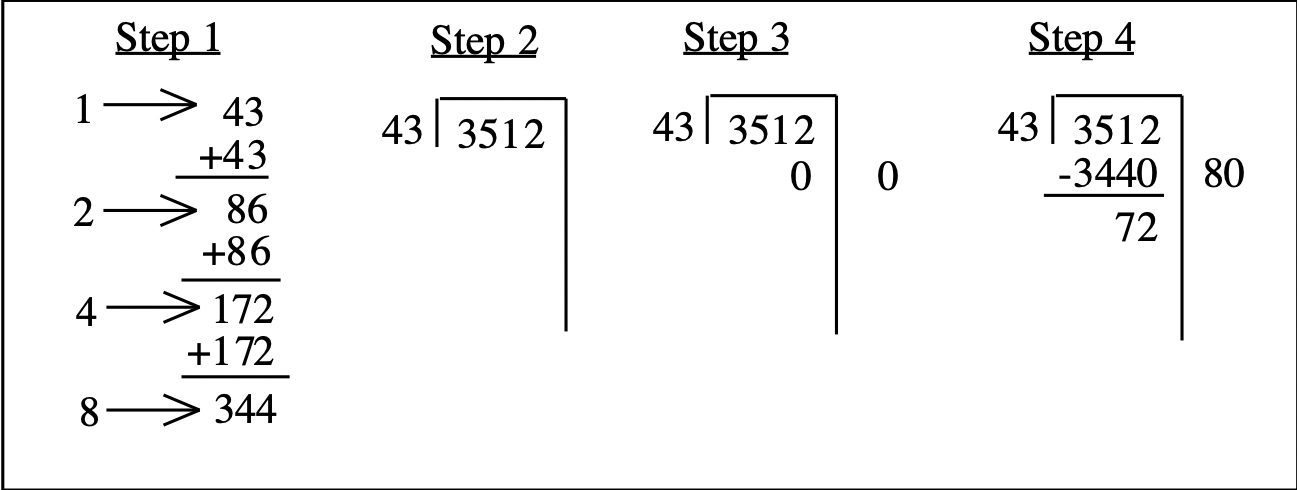
Step 5: Now we have to see how many more 43's can be subtracted from 72. There are no extra zeroes to tack on this time, as in step 4. We can subtract 1 more 43 from 72, so write a 1 to the right of the scaffold, and subtract 43 from 72 to get 29.

Steps 6, 7 and 8: Since 29 is less than 43, that is the remainder, so add up the numbers on the right of the scaffold to get the quotient.Write the answer as a quotient and remainder in a box up at the top of the problem. Check the answer. You can use a calculator to multiply 81 times 43, which is 3483, and then add 29.

The last four steps are shown below.

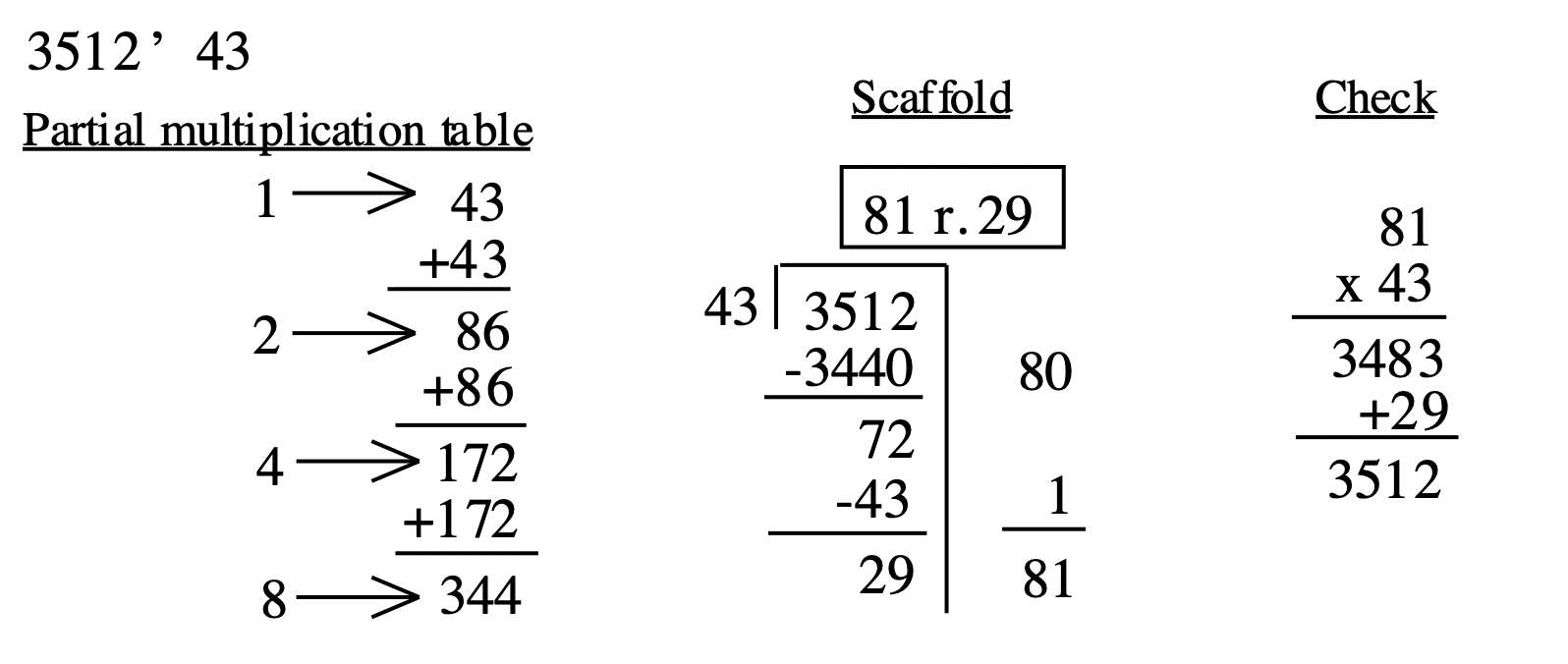
If you were to show your work, this is what the whole problem would look like:

Here's what it would look like doing it the way you did it in exercise 2:

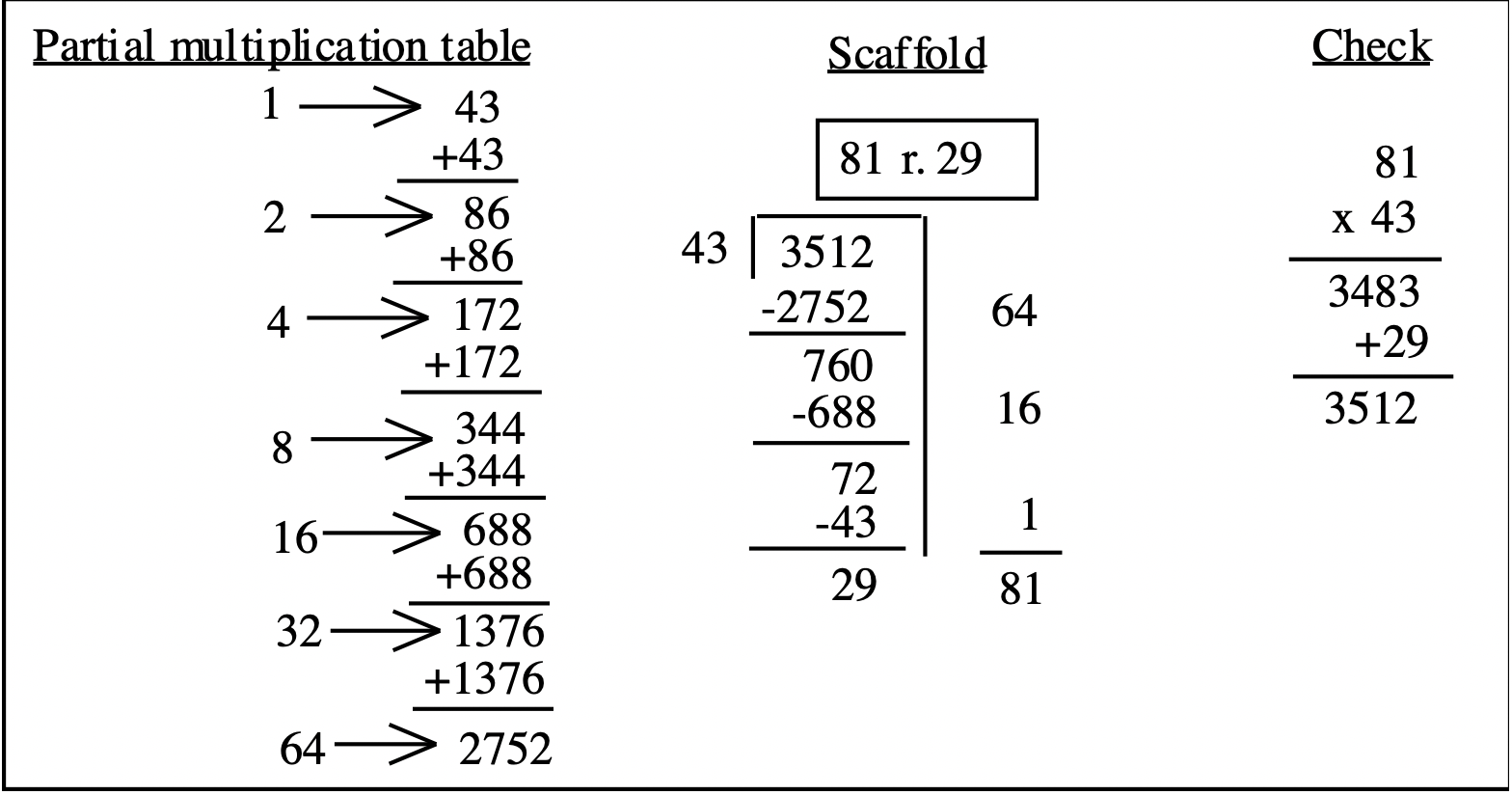
For both methods, when you add the numbers on the right of the scaffold to get the quotient, be careful to line up the place values! Both methods produce the same result and work equally well. What's important is that the procedure makes sense to you!

Two more examples using multiples of tens (putting in the extra zeroes) is shown below.

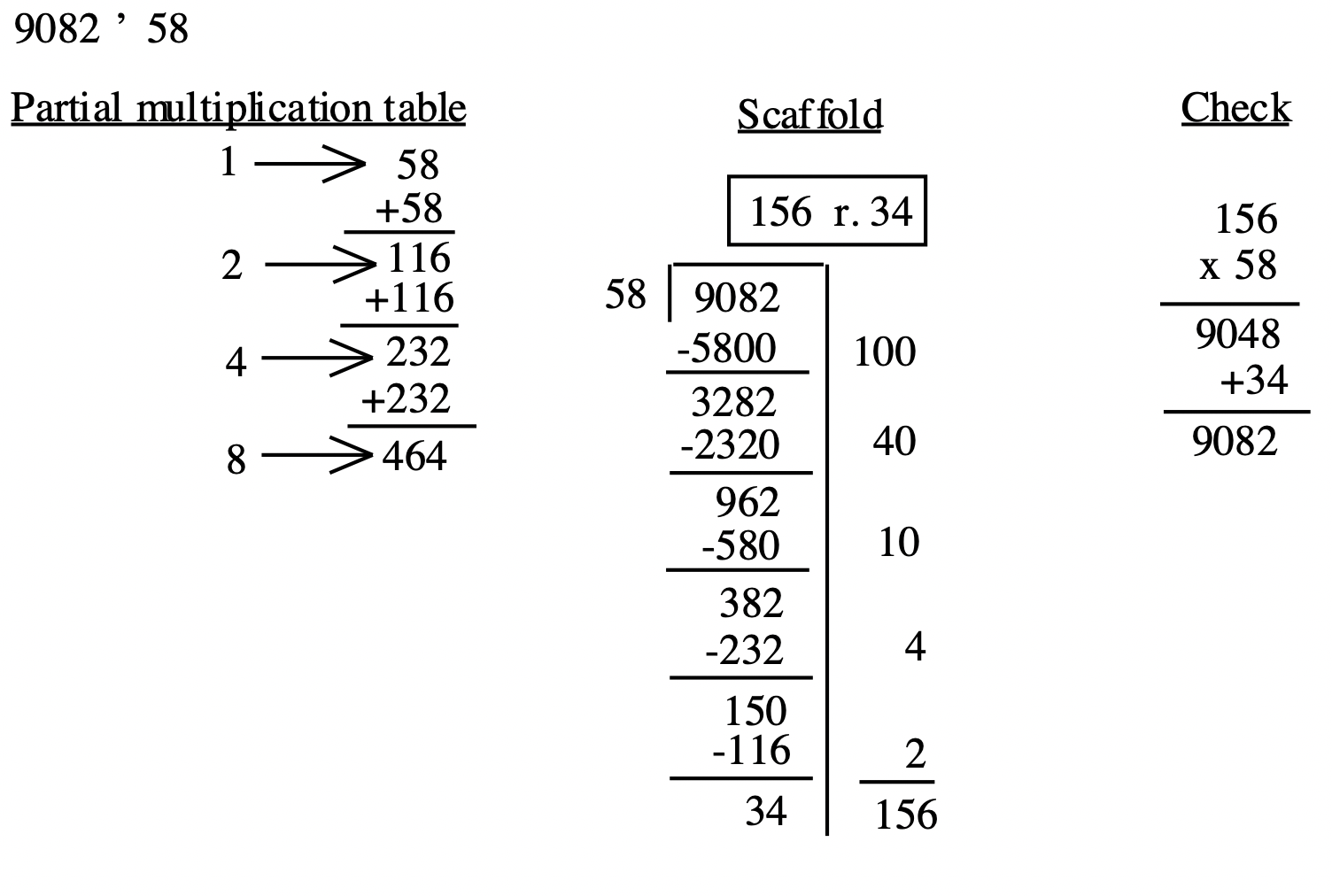
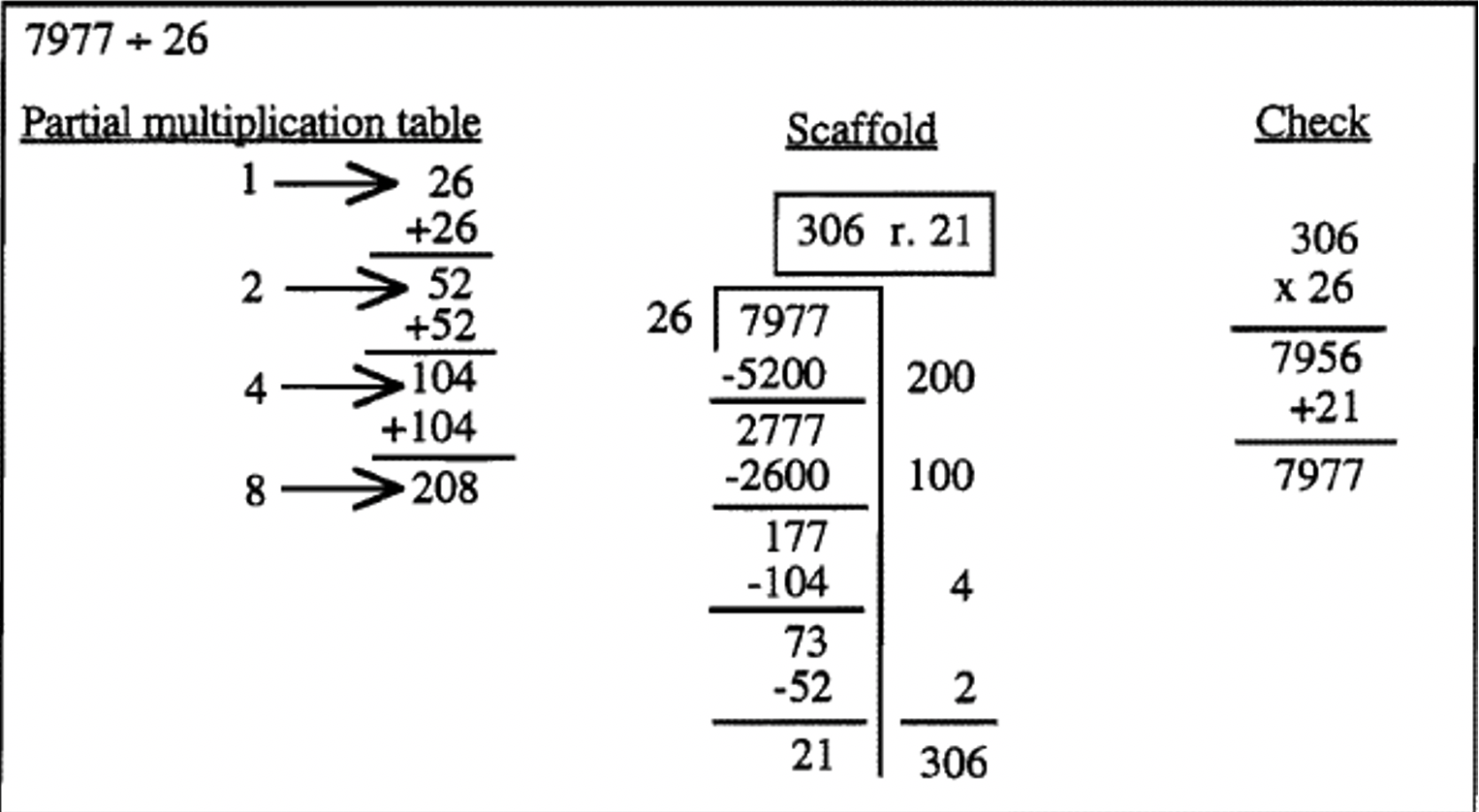
In the above example, many people (children and adults) miss writing the zero in the tens place for the answer of 306 when they do it the short division way it is usually taught. A very common answer to this problem is 36 r. 21. In the first step above, writing the full number on the side really emphasizes the fact that you aren't just multiplying 26 by a 2 to get 52 you are multiplying 26 by 200 to get 5200. You know the answer to the problem will be more than 200 since you already subtracted 200 26's from 7977. When you have 177 left, you simply note you can only subtract a few more 26's. If one neatly writes the numbers on the right, there are no numbers in the tens place to add up. The confusion about the zero doesn't even come up!

Exercise 3

For each division problem, make a partial multiplication table up to 8 times the divisor. Then, draw a scaffold, and use repeated subtraction to do each division. Use multiples of tens (putting in extra zeroes where necessary) to do these problems. Then, check the answer. All work should be shown in the space provided. After checking, write the answer on the space provided at the beginning of the problem. A calculator may be used to check the answer, but write down the steps.

a. \(1230 \div 27\) = ______________ Partial multiplication table: Scaffold: Check:

b. \(603 \div 48\) = _______________ Partial multiplication table: Scaffold: Check:

c. \(1346 \div 41\) = ______________ Partial multiplication table: Scaffold: Check:

d. \(3512 \div 43\) = ______________ Partial multiplication table: Scaffold: Check:

e. \(66289 \div 325\) = ____________ Partial multiplication table: Scaffold: Check:

f. \(5222 \div 21\) = ______________ Partial multiplication table: Scaffold: Check:

Doing the partial multiplication table on the side, in conjunction with the repeated subtraction method, is completely optional. But, if you make up the table first, you do not need to do any multiplying or estimating in your head. Another option is to skip doing the partial multiplication table altogether and still use the repeated subtraction method. In this case, if you aren't sure how many times the divisor can be subtracted, underestimate at each step that you aren't absolutely sure how many of the divisor to subtract. In other words, make sure you don't multiply something by the divisor and come out with a number too big to subtract from the dividend. Underestimating is okay with the repeated subtraction method because you just subtract some more at the next step. For instance, in the previous example, you could have subtracted 200 26's (5200) at the first step and then 100 more 26's at the second step, or you could have subtracted 300 26's at the first step by multiplying 26 by 3 in your head if you were sure that 26 times 3 wasn't too big. I like the partial multiplication table because it takes the guesswork out of the problem. In the example in the box below, the division is done using repeated subtraction without making up a table Instead, you estimate how many of the divisor can be subtracted at each step. In this case, the multiplication must be done in your head, or on the side, as you go along.

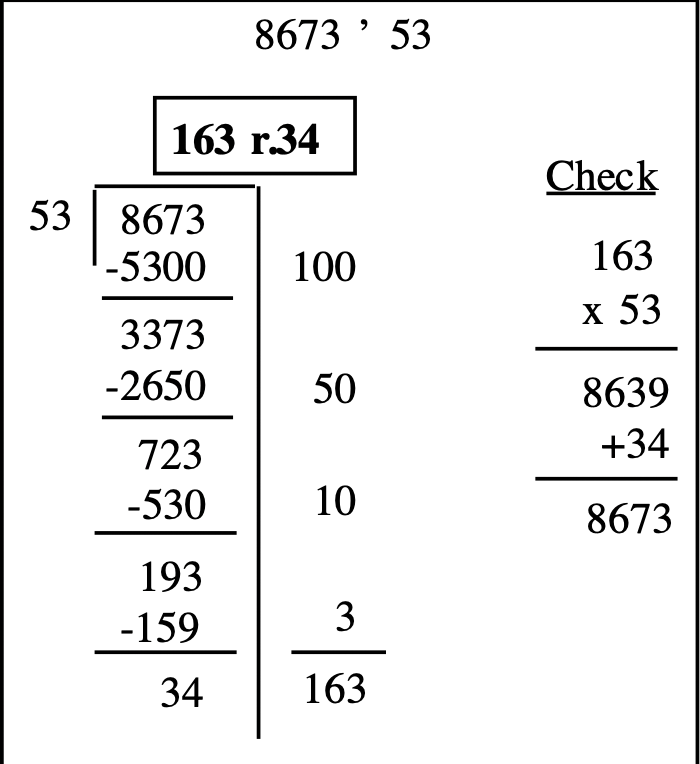
Here is a way to divide \(8673 \div 53\) without the usual prep work of making up a partial multiplication table first. This means the multiplication must be done along the way. It's important to note that it is okay to underestimate when using the repeated subtraction method (unlike the traditional division method), because you can always subtract more at the next step. On the other hand, overestimating will cause you to go back and redo the problem. First I note that 53 goes into 86 one time, so I subtract 100 53's, or 5300, from 8673. Next, estimate \(337 \div 53\). Since I'm not sure if it is 5 or 6 times, I play it safe and therefore, estimate 5. So, I subtract 50 times 53, or 2650, from 3373. (Note I have to do the multiplication in my head.) Well, I see another 53 can be subtracted from 72, so I subtract 10 times 53, or 530, from 723. Then, I estimate 53 goes into 193 at least 3 times, so I subtract 3 times 53 from 193. Since 34 is less than 53, 34 is the remainder. Add the numbers on the side to get the quotient of 163. Check by multiplying \(53 \times 163\) and adding the remainder of 34 to get 8673.

In the traditional division algorithm, there is no room for underestimating or overestimating. You have to go back and erase if you put the wrong digit in a particular place value. If you estimate incorrectly, the multiplication you do ends up being a waste of time and effort, and you have to start over. Also, most people don't think about what or why they are putting digits in a particular place. They don't think about the place values, or that division is really about repeated subtraction. I think the scaffold method, with or without making up a partial multiplication table, promotes a better understanding of division, and is less stressful than the traditional "guess" method where there is absolutely no room for error. The one advantage to the traditional algorithm is that it is a shortcut to the scaffold method, and it uses less space on paper.

In the end, it's really up to the individual doing the division to decide which way to do it.

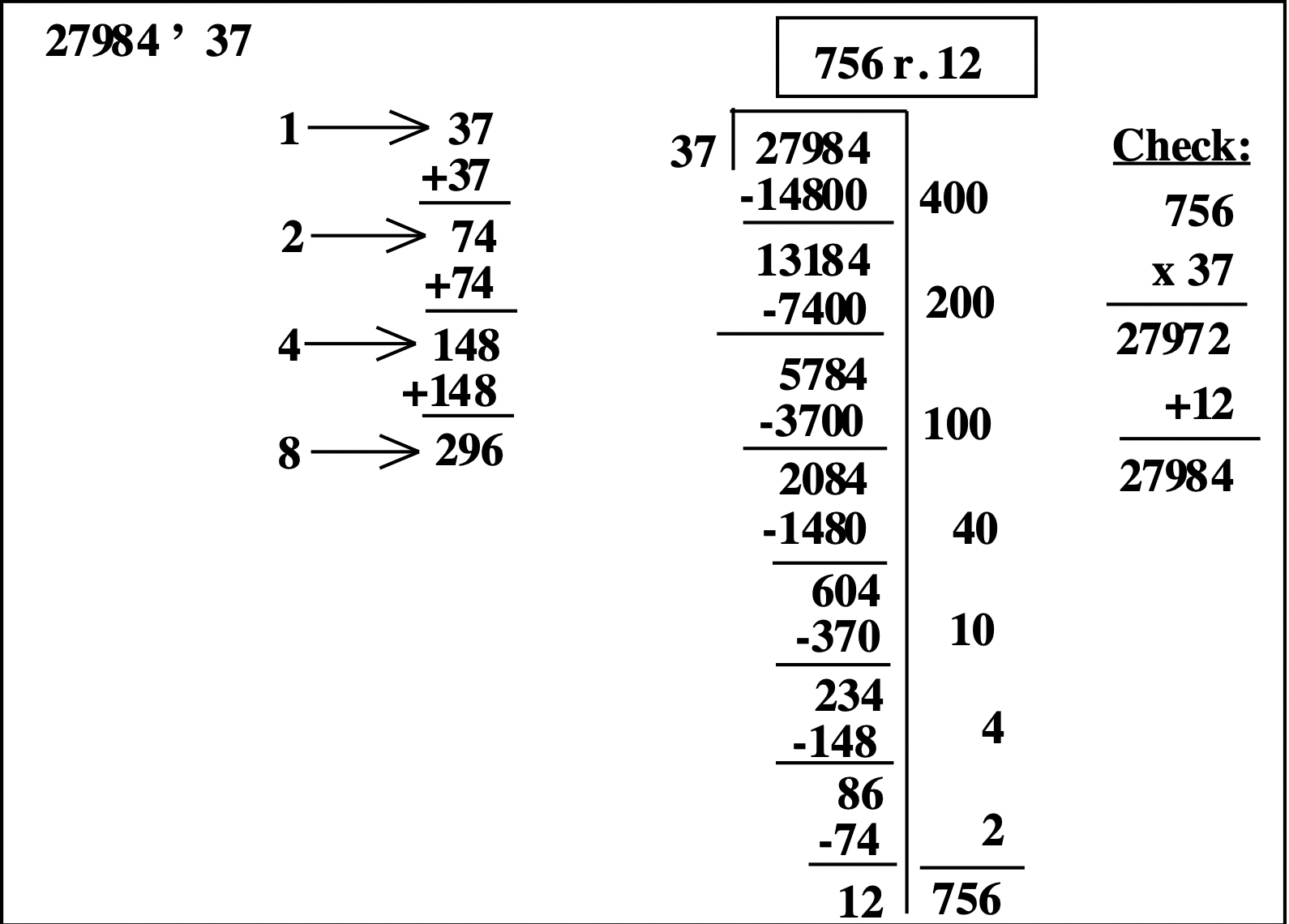
Here is an example of dividing \(27984 \div 37\) using the doubling method.

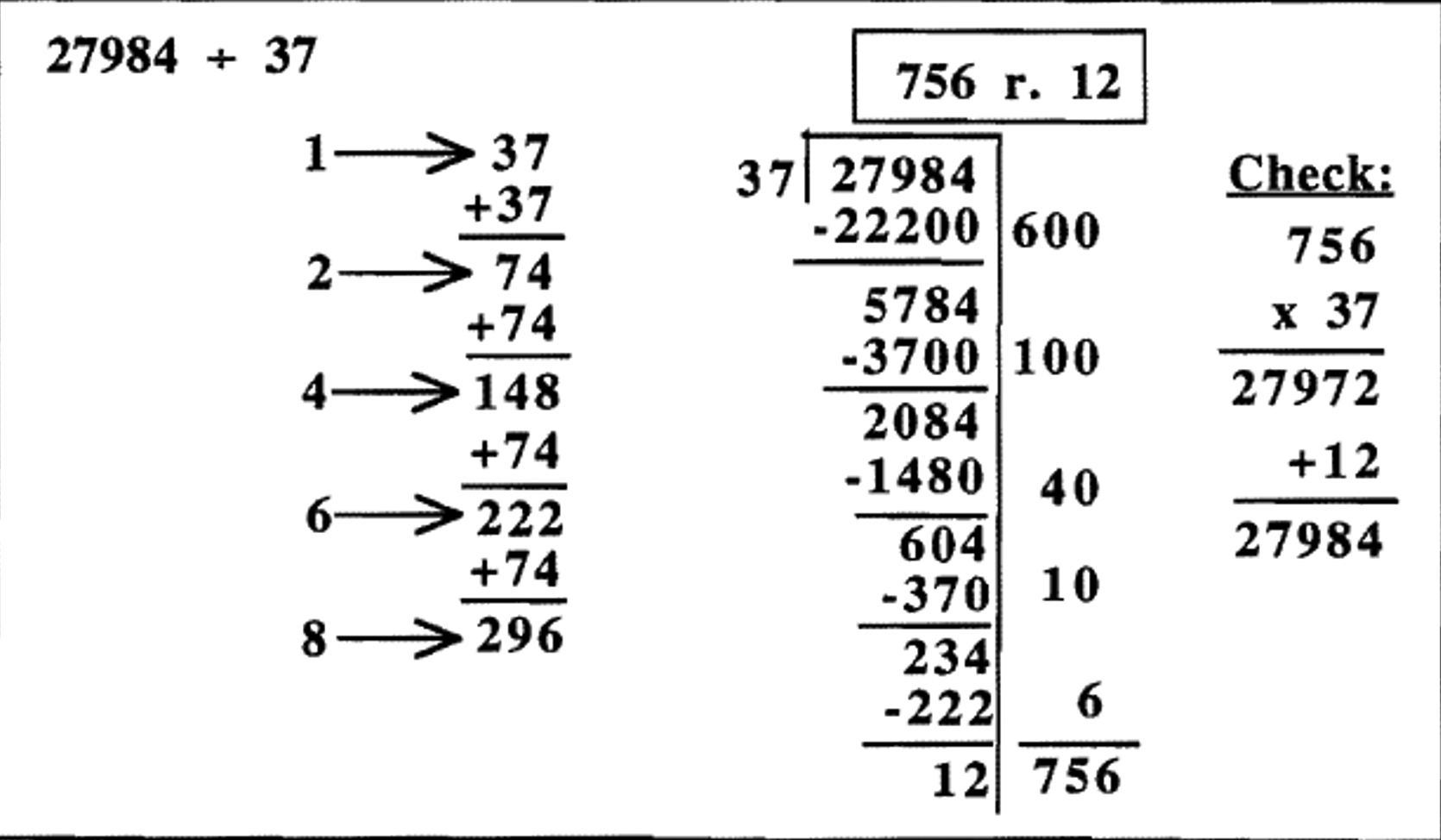
When making up a multiplication table, it doesn't have to be partial. In base ten, doubling to get the divisor times 1, 2, 4 or 8 gives us close enough estimates most of the time. The worst possible case is that 7 is the correct number of times something can be subtracted, as in the above example. In that case, we would first subtract 4, then 2, then 1. That doesn't happen too often, but once in awhile it does. Another strategy is to add one more addition to the partial table so you also know what 6 times the divisor is. To do this, after figuring what 4 times the divisor is, add 2 more, as shown below (add 74 instead of doubling 148), then add 2 more again (add 74 again) to get 8 times the number. Look at the difference.

In fact, we could have used repeated addition to find out the answers to the divisor being multiplied by each digit from 1 to 9, in which case neither underestimating nor overestimating would ever occur. Although this leaves absolutely no guesswork at all, it's more work than necessary in most cases. Here is an example of how someone could do the same problem done on the previous page by making a complete multiplication table first. It's easy to do the division if you do this first, but there is a lot of prep work at the beginning to make the table.

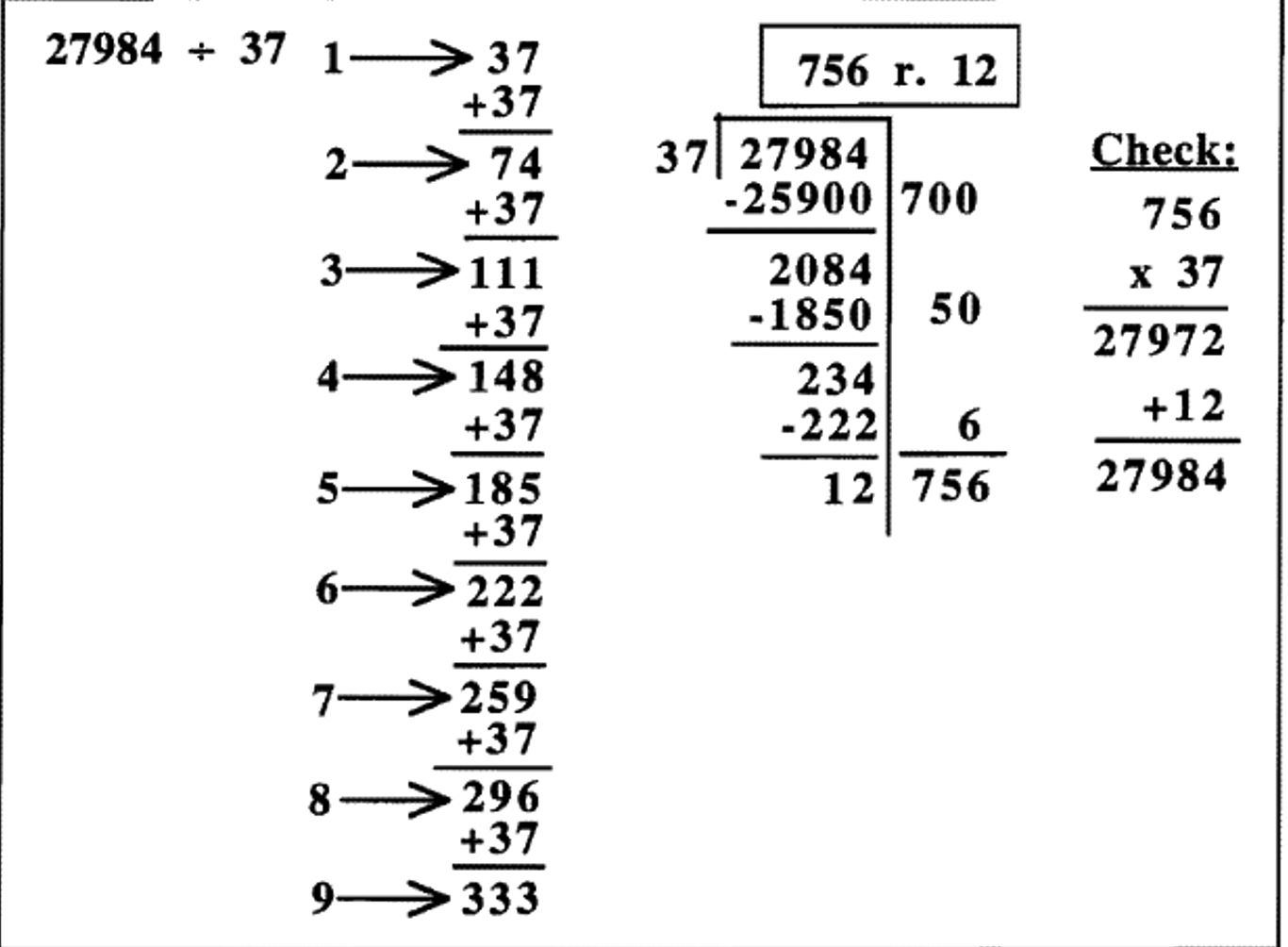
Look back at the three different ways the division \(27984 \div 37\) was done. The first way, shown on the previous page, had a short partial multiplication table (only three additions for prep work), but the repeated subtraction method took a little longer. It required seven subtractions to get the answer (look to the right of the scaffold), because the 700 took three steps 400, 200, 100; the 50 took two steps 40 and 10; and the 6 took two steps 4 and 6. The second way had one more addition for the prep of the multiplication table, and then only required five subtractions to get the answer (look to the right of the scaffold), because the 700 took two steps 600, and 100; the 50 took two steps 40 and 10; and the 6 took one step. The third way, shown at the top, required eight additions of prep work to make the multiplication table, but the division was a breeze, taking only three steps. If you do it this way, you may as well write the 756 up at the top, as you do when you do it using the traditional algorithm because you can never underestimate or overestimate.

Depending on the particular problem, one method may be faster than another, but many times you wouldn't know until you've completed the problem. I usually just do the doubling to 8 to get good enough estimates, but if you'd like to make a more complete table, it works just as well. You have to decide if you prefer to do more prep work up front to possibly make the division faster.