9.2: Rational Numbers
- Page ID
- 70334
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Materials: Fraction Circles, Fraction Arrays, Multiple Strips, C-strips
Use your marked fraction circles to do these first few activities.
Take one wedge from each fraction circle (1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10, and 1/12). One fraction is bigger than another if it covers more space than the other fraction. Compare them and put them in order from smallest to largest, and write them in order below, using the less than symbol ( < ).
From what you discovered in exercise 1, circle the larger fraction in each case.
| a. 1/90 or 1/95 | b. 1/32 or 1/33 |
If you take 5 of the fraction pieces that say 1/8, then together you have 5/8. Use this fact to do the next exercise.
Use the fraction circles to compare 5/6, 5/8, 5/9, 5/10, and 5/12. Put them in order from smallest to largest using the less than symbol ( < ).
From what you discovered in exercise 3, circle the larger fraction in each case.
| a. 15/37 or 15/40 | b. 89/100 or 89/200 |
Use the fraction array to order these fractions: 4/5, 4/6, 4/7, 4/8, 4/9, 4/10, 4/11 and 4/12. Put them in order from smallest to largest using the less than symbol ( < ).
Explain the pattern you learned from doing exercises 1-5.
Use fraction circles to compare these fractions: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10, and 11/12. Put them in order from smallest to largest using the less than symbol ( < ).
Use the fraction array to order these fractions: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10, 11/12. Put them in order from smallest to largest using the less than symbol ( < ).
From what you discovered in exercises 7 and 8, circle the larger fraction in each case.
| a. 89/90 or 94/95 | b. 56/57 or 31/33 |
Order these fractions: 45/46, 71/72, 34/35, 99/100, 25/26, 13/14, 51/52. Put them in order from smallest to largest using the less than symbol ( < ).
Explain the pattern you learned from doing exercises 7 - 10.
Draw a model of your own that would help to convince someone why 4/5 was bigger than 2/3.
A rational number is simply the formal name for a fraction. Below is a formal definition of a rational number.
A rational number is a number that can be written as the quotient (ratio) of an integer, \(m\), and a nonzero integer, \(n\), which is written like this: \(\frac{m}{n}\).
When written in this form, \(m\) is called the numerator and \(n\) is called the denominator. If GCF(\(m,n\)) = 1 (i.e., \(m\) and \(n\) have no factors in common), then the rational number is said to be in simplest (or reduced) form.
The following is one way to represent a rational number, \(\frac{m}{n}\).
Divide a (defined) unit into an equal number of \(n\) parts or subsets. Which means \(n\) parts make up a whole. Each one of these parts (or subsets) represents \(\frac{1}{n}\). Then, \(m\) of those parts represents \(\frac{m}{n}\).
For each rational number, \(\frac{m}{n}\),
- Define a unit in terms of dots. State the value of each dot.
- Divide the unit into an equal number (the denominator) of parts.
- Show a representation of \(\frac{1}{n}\).
- Show a representation of \(\frac{m}{n}\).
- Define the unit differently, and do the three parts (i, ii and iii) again.
|
a. Let one unit be defined by 8 dots, as shown below. Each dot = 1/8 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. The unit is divided into 8 equal parts, as shown below.  ii. Below is a representation of 1/8, which is one of the equal parts shown in part b. \[\boldsymbol{\cdot}\nonumber \] iii.Below is a representation of 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b. Let one unit be defined by 16 dots, as shown below. Each dot = 1/16 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. The unit is divided into 8 equal parts, as shown below.  ii. Below is a representation of 1/8, which is one of the equal parts shown in part b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] iii.Below is a representation of 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Notice there are 3 dots for the answer in part a, where each dot represents 1/8. So, the 3 dots represents the number 3/8. For part b, the answer has 6 dots. Since each dot represents 1/16, this also represents 6/16. Therefore, 3/8 and 6/16 must represent the same number. Two fractions that represent the same number are called equivalent fractions.
It is crucial to define your unit before beginning any exercise!!
|
a. Let one unit be defined by 5 dots, as shown below. Each dot = 1/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. The unit is divided into 5 equal parts, as shown below.  ii. Below is a representation of 1/5, which is one of the equal parts shown in part b. \[ \boldsymbol{\cdot} \nonumber \] iii.Below is a representation of 2/5. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b. Let one unit be defined by 10 dots, as shown below. Each dot = 1/10 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. The unit is divided into 5 equal parts, as shown below.  ii. Below is a representation of 1/5,which is one of the equal parts shown in part b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] iii.Below is a representation of 2/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Notice there are 2 dots for the answer in part a, where each dot represents 1/5. So, the 2 dots represents the number 2/5. For part b, the answer has 4 dots. Since each dot represents 1/10, this also represents 4/10. Therefore, 2/5 and 4/10 must represent the same number. Two fractions that represent the same number are called equivalent fractions.
IT IS CRUCIAL TO DEFINE YOUR UNIT BEFORE BEGINNING ANY EXERCISE!!
Use the method in the last two examples to show two different representations for 3/4.
Use your fraction arrays to determine all fractions on the fraction array that are equivalent to 1/2. Do this by finding 1/2 on the array, and seeing what other numbers are the same length.
Use your fraction arrays to determine all fractions on the fraction array that are equivalent to 2/3. Do this by finding 2/3 on the array, and seeing what other numbers are the same length.
You'll now be using your multiple strips to identify equivalent fractions. To use your strips, you need to cut out the strips by rows. To find fractions equivalent to 3/7, align the 3 strip above the 7 strip as shown below:
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
Now, you can see eleven other equivalent fractions for 3/7: 6/14, 9/21, 12/28, 15/35, 18/42, 21/49, 24/56, 27/63, 30/70, 33/77, and 36/84.
Use your multiple strips to write 6 fractions equivalent to 2/9
Use your multiple strips to write 6 fractions equivalent to 4/5
What is the rule for finding a fraction equivalent to a given fraction? Give an example how to find some fractions that are equivalent to 5/6.
We are now going to work again with models, using dots, to compare two fractions, add two fractions, subtract two fractions, or multiply or divide two fractions. For each problem, it is CRUCIAL that you begin each problem by explicitly stating the following:
1. Be specific about what you are using for the unit. It will be easiest if you use an array of dots, where the denominator of one fraction is the number of rows in the array, and the denominator of the other fraction is the number of columns in the array.
2. State the value of each dot, each column and each row.
Okay, let's go on to an example: Use models to compare 2/5 and 3/7.
|
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of 35 dots, as shown below. Since there are 35 dots to a unit, each dot = 1/35 of a unit. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts by circling the rows, as shown below:  Therefore, each row is 1/5 of a unit. Notice there are 7 dots in 1/5 of a unit: 1/5 = \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 3: Similarly, since there are 7 equal columns, each column is 1/7 of a unit: 1/7 = \[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Step 4: Now that we have properly defined the unit, we are ready to show what 2/5 looks like. Since 1/5 is 1 row of dots, then 2/5 must be 2 rows of dots. Therefore, 2/5 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 2/5 contains 14 dots, which is equivalent to 14/35. |
Step 5: Similarly, we can show what 3/7 looks like. Since 1/7 is 1 column of dots, then 3/7 must be 3 columns of dots. Therefore, 3/7 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 3/7 contains 15 dots, which is equivalent to 15/35. |
Since 2/5 contains less dots than 3/7, 2/5 must be less than 3/7. Answer: 2/5 < 3/7.
Compare 3/4 and 4/5 using models. Show all of the steps, and explain the procedure as shown in the previous example.
Okay, let's go on to an example of addition: Use models to add 2/5 and 3/7.
|
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of 35 dots, as shown below. Since there are 35 dots to a unit, each dot = 1/35 of a unit. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts by circling the rows, as shown below:  Therefore, each row is 1/5 of a unit. Notice there are 7 dots in 1/5 of a unit: 1/5 = \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 3: Similarly, since there are 7 equal columns, each column is 1/7 of a unit: 1/7 = \[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Step 4: Now that we have properly defined the unit, we are ready to show what 2/5 looks like. Since 1/5 is 1 row of dots, then 2/5 must be 2 rows of dots. Therefore, 2/5 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 2/5 contains 14 dots, which is equivalent to 14/35. |
Step 5: Now, we add the two models together, as shown below. The answer is 29/35. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 3/7 contains 15 dots, which is equivalent to 15/35. |
Step 5: Now, we add the two models together, as shown below. The answer is 29/35.
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} + \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 29 \text{ dots } = 29/35 \nonumber \]
Add 1/4 and 2/5 using models. Show all of the steps, and explain the procedure as shown in the previous example.
Okay, let's go on to an example of subtraction: Use models to do the following subtraction: 3/7 – 2/5.
|
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of 35 dots, as shown below. Since there are 35 dots to a unit, each dot = 1/35 of a unit. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts by circling the rows, as shown below:  Therefore, each row is 1/5 of a unit. Notice there are 7 dots in 1/5 of a unit: 1/5 = \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 3: Similarly, since there are 7 equal columns, each column is 1/7 of a unit: 1/7 = \[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Step 4: Now that we have properly defined the unit, we are ready to show what 2/5 looks like. Since 1/5 is 1 row of dots, then 2/5 must be 2 rows of dots. Therefore, 2/5 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 2/5 contains 14 dots, which is equivalent to 14/35. |
Step 5: Similarly, we can show what 3/7 looks like. Since 1/7 is 1 column of dots, then 3/7 must be 3 columns of dots. Therefore, 3/7 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Notice that 3/7 contains 15 dots, which is equivalent to 15/35. |
Now, we subtract, as shown below. The answer is 1/35.
\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} - \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 1 \text{ dot } = 1/35 \nonumber \]
Do the following subtraction using models: 7/8 – 2/3. Show all of the steps, and explain the procedure as shown in the previous example.
Multiplying fractions is a little bit trickier. The repeated addition model doesn't make sense when you are multiplying two fractions. When you see two fractions multiplied together, like 2/5 \(\cdot\) 3/7, think of this as 2/5 OF 3/7. In other words, you have to take 3/7 of a unit, and then you have to take 2/5 of that. Note that you have to represent the second fraction BEFORE you can do the multiplication.
Okay, let's go on to an example of multiplication: Use models to do the following multiplication: 2/5 \(\cdot\) 3/7.
|
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of 35 dots, as shown below. Since there are 35 dots to a unit, each dot = 1/35 of a unit. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts. Therefore, each row is 1/5 of a unit. Notice there are 7 dots in 1/5 of a unit: 1/5 = \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 3: Similarly, since there are 7 equal columns, each column is 1/7 of a unit: 1/7 = \[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Step 4: Now that we have properly defined the unit, we first have to show what 3/7 (the second number in the multiplication) looks like. Since 1/7 is 1 column of dots, then 3/7 must be 3 columns of dots. Therefore, 3/7 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 5: This is where there is a difference in how you proceed. You now need to find 2/5 of the 3/7 that is shown in step 4. Since there are 5 rows of dots in step 4, each row (of 3 dots) represents 1/5. So, you only want 2 rows of the dots from step 4, as shown below. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] This is the answer. There are 6 dots, so this represents 6/35. |
Multiplication can be shown all on one unit by first showing the unit, second circling the part that represents the second fraction in the multiplication, and then circling the part that represents the first fraction in the multiplication. Below is the sequence of steps for this problem.
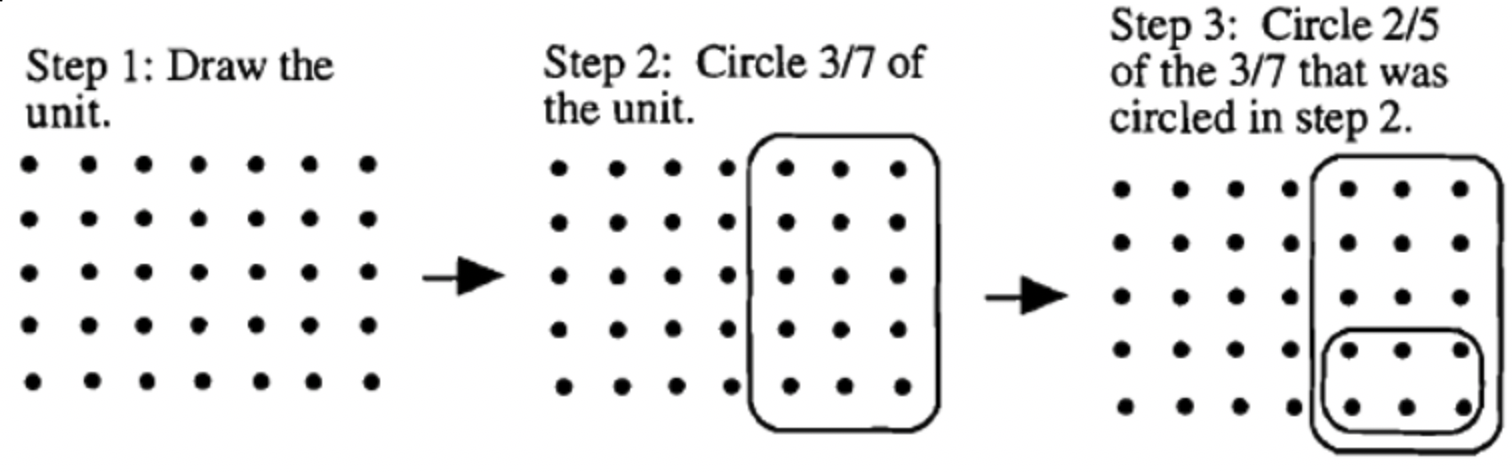
Okay, let's see what it looks like if we switch the order of the fractions: Use models to do the following multiplication: \(\bf 3/7 \cdot 2/5\).
|
Step 1: Let 1 unit = 5 rows of dots by 7 columns of dots, for a total of 35 dots, as shown below. There are 35 dots to a unit, so each dot = 1/35 of a unit. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 2: Since there are 5 rows, the unit can be broken up into 5 equal parts. Therefore, each row is 1/5 of a unit. Notice there are 7 dots in 1/5 of a unit: 1/5 = \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 3: Similarly, since there are 7 equal columns, each column is 1/7 of a unit: 1/7 = \[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Step 4: Now that we have properly defined the unit, we first have to show what 2/5 (the second number in the multiplication) looks like. Since 1/5 is 1 column of dots, then 2/5 must be 2 columns of dots. Therefore, 2/5 is shown below: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Step 5: You now need to find 3/7 of the 2/5 that is shown in step 4. Since there are 7 columns of dots in step 4, each column (of 2 dots) represents 1/7. So, you only want 3 rows of the dots from step 4, as shown below. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] This is the answer. There are 6 dots, so this represents 6/35. |
Again, this multiplication can be shown all on one unit by first showing the unit, second circling the part that represents the second fraction in the multiplication, and then circling the part that represents the first fraction in the multiplication. Below is the sequence of steps for this problem.
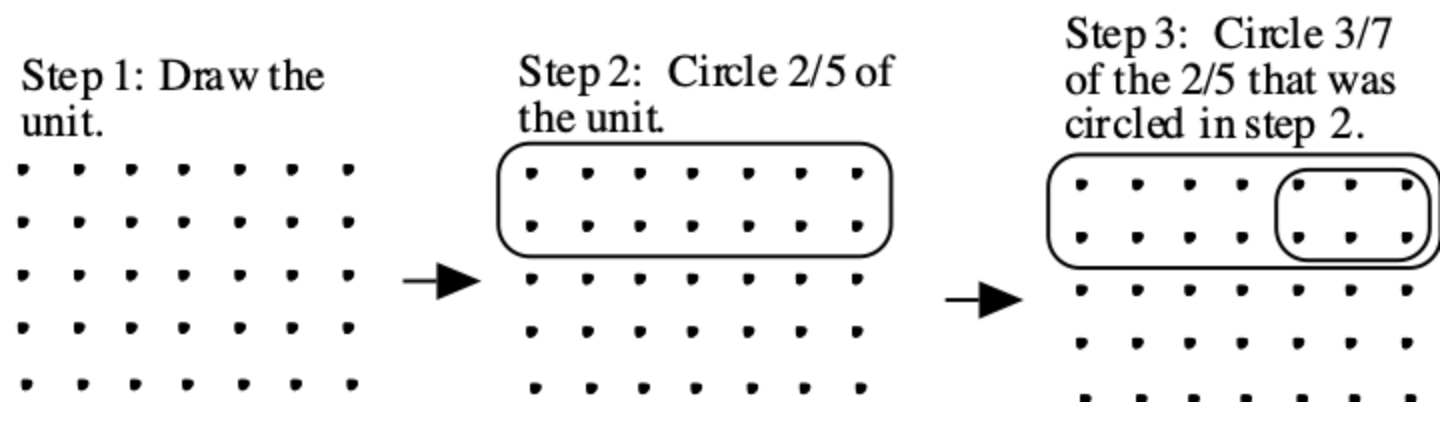
Although the answer is the same for 3/7 \(\cdot\) 2/5, and 2/5 \(\cdot\) 3/7, the sequence of steps is not. Note the difference between step 3 above (3/7 \(\cdot\) 2/5) and step 3 below (2/5 \(\cdot\) 3/7).
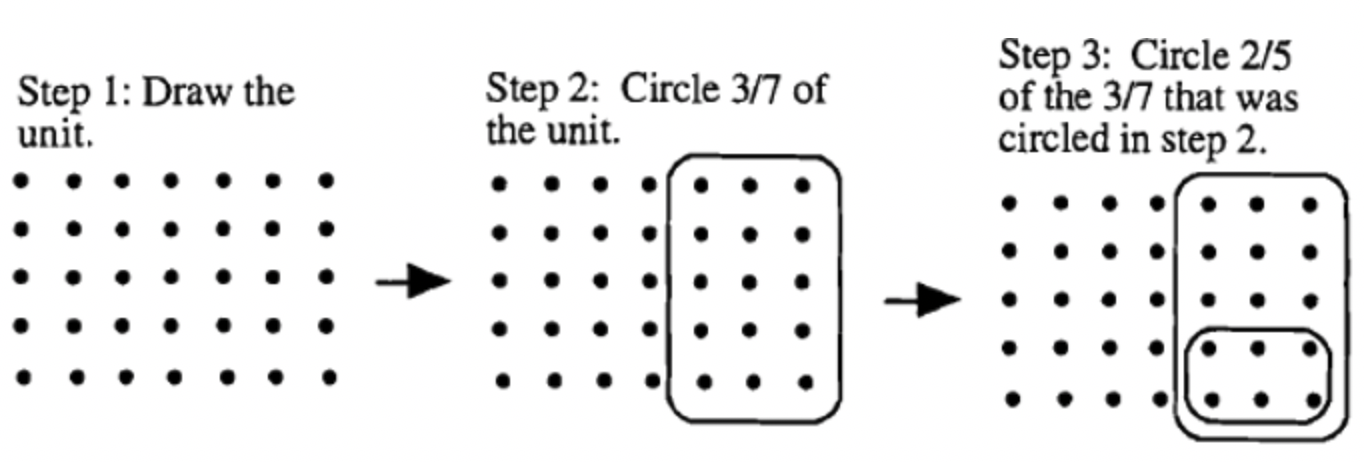
Do the following multiplications using models. Show all of the steps, and explain the procedure as shown in the previous examples.
a. 4/5 \(\cdot\) 2/3
b. 3/4 \(\cdot\) 5/6
By looking at the final drawing someone made to model a multiplication of two fractions, determine which multiplication was performed, and then state the answer. Circle which multiplication represents the correct choice.
|
a. 5/6 \(\cdot\) 2/3 OR 2/3 \(\cdot\) 5/6 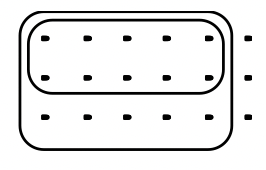 |
b. 1/2 \(\cdot\) 7/8 OR 7/8 \(\cdot\) 1/2 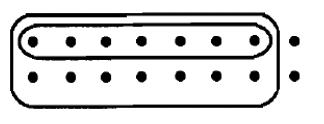 |
If all of the dots shown for each problem represent 1 unit, determine the multiplication problem that someone did to get the answer, and state the answer.
 a. a. |
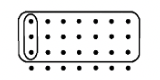 b. b. |
Another model you can use to do multiplication is the C-strips, although it is somewhat limiting.
Multiply \(3/4 \cdot 1/2\).
Solution
This means 3/4 of 1/2 of a unit. So, we'll have to define an appropriate unit, first take 1/2 of the unit, and then take 3/4 of the answer obtained after taking 1/2. The choice for 1 unit using C-strips is to multiply the denominators together to get the length of the unit rod you need. In this case, 4 \(\cdot\) 2 = 8, so choose the Brown C-strip as the unit.
Let 1 unit = N. First, take 1/2 of Brown (N), which is purple (P). Then, take 3/4 of purple, which is light green (L). The answer, L, represents 3/8, since the unit C-strip was N. Therefore, 3/4 \(\cdot\) 1/2 = 3/8.
Multiply \(1/2 \cdot 3/4\).
Solution
This means 1/2 of 3/4 of a unit. So, we'll have to define an appropriate unit, first take 3/4 of the unit, and then take 1/2 of the answer obtained after taking 3/4. The choice for 1 unit using C-strips is to multiply the denominators together to get the length of the unit rod you need. In this case, 4 \(\cdot\) 2 = 8, so choose the Brown C-strip as the unit.
Let 1 unit = N. First, take 3/4 of Brown (N), which is dark green (D). Then, take 1/42 of dark green (D), which is light green (L). The answer, L, represents 3/8, since the unit C-strip was N. Therefore, 1/2 \(\cdot\) 3/4 = 3/8.
Multiply \(2/3 \cdot 4/5\).
Solution
This means 2/3 of 4/5 of a unit. So, we'll have to define an appropriate unit, first take 4/5 of the unit, and then take 2/3 of the answer obtained after taking 4/5. The choice for 1 unit using C-strips is to multiply the denominators together to get the length of the unit rod you need. In this case, 3 \(\cdot\) 5 = 15. There isn't one C-strip that long, so use and orange + yellow as the unit.
Let 1 unit = O + Y. First, take 4/5 of O + Y, which is hot pink (H). Then, take 2/3 of hot pink (H), which is brown (N). The answer, N, represents 8/15, since the unit C-strip was O + Y. Therefore, 2/3 \(\cdot\) 4/5 = 8/15.
Use the C-strips to multiply 1/3 \(\cdot\) 3/4. Explain the steps.
The process of doing multiplication using C-strips can be shown in a chart. I've shown the steps for the above three examples on the next page.
Fill in the chart showing how to do the following multiplications using C-strips. The multiplication is in the first column. State an appropriate choice for the unit (name a C-strip, or sum of two C-strips) in the second column. Write the C-strip obtained after the first part of the multiplication (which is the second fraction as a part of the unit) in the third column. Then, do the final multiplication, and write the C-strip obtained in the fourth column. In the fifth column, write a fraction using C-strips putting the final unit obtained in the fourth column as the numerator, and the unit in the denominator. Then, in the last column, write the answer as a fraction. Do not simplify.
| Example | \(3/4 \cdot 1/2\) | N | P | L | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Example | \(1/2 \cdot 3/4\) | N | D | L | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Example | \(2/3 \cdot 4/5\) | O+Y | H | N | \(\frac{N}{O+R}\) | \(\frac{8}{15}\) |
| a. | \(1/3 \cdot 3/4\) | |||||
| b. | \(1/2 \cdot 1/4\) | |||||
| c. | \(3/2 \cdot 1/4\) | |||||
| d. | \(2/3 \cdot 1/2\) |
On to Division with Rational Numbers...
Remember that the answer to the division \(\bf a \div b\) can be obtained by answering this question: "How many sets of b are contained in a?"
Let's use this idea to find the answer to the following division problem:
Use a model to compute: \(\bf 3 \div 1/2\)
Solution
The answer to \(\bf 3 \div 1/2\) is the answer to this question: How many 1/2's are contained in 3? Below are two possible methods you can use to find the solution.
Method 1: Let 1 unit = 1 square. Then count how many 1/2's are contained in 3 squares.
Draw three squares to represent 3. Then, divide each square into 1/2's. Count how many 1/2's are in the 3 squares. From the model, it is clear there are 6 1/2's in 3 squares. So the answer to 3 \(\div\) 1/2 is 6.
Method 2: Let the unit be defined similarly to how we did it for the previous problems.Multiply the denominators together to determine how many dots are in a unit. In this case, 3 is the same as 3/1. Let the unit = 1 row of dots by 2 columns of dots for a total of 2 dots.
Unit = \(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) Then represent the number 3 based on this unit, and the number 1/2 based on this unit.
3 = 3 sets of 2 dots = \(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) and 1/2 = 1/2 of the 2 dots = \(\boldsymbol{\cdot}\)
In the set representing 3, circle as many sets as possible that represent 1/2: \(\begin{matrix} \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} \end{matrix}\)
Count how many 1/2's are in 3. There are 6 1/2's in 3, so the answer is 6.
Method 3: Let 1 unit = the dark green C-strip. Represent 3 and 1/2 as a C-strip based on this unit. Since 3 = 3 dark green C-strips, then 3 = the orange + brown C-strip (or 3 dark greens, or hot pink + dark green). Since 1/2 of the dark green C-strip is light green, then 1/2 = the light green C-strip.
We have to answer the question: How many 1/2's are in 3? Since 1/2 = L, and 3 = O + N, count how many light green C-strips make up the length of the O + N C-strip. There are 6. Once again, the answer is 6.
| Unit: | D |
|---|
| 3: | H | D |
|---|
| 1/2 | L |
|---|
Here is how to get the answer. Show how many light greens are contained hot pink + dark green.
| L | L | L | L | L | L |
Notice that you begin by defining a unit C-strip, and then use that unit to define the two numbers in the division problem. But you do NOT refer back to the unit to compute the division problem. You simply count how many of the divisor (second C-strip) is in the dividend (first C-strip).
Use a model to compute: \(\bf 1/2 \div 1/4\).
Solution
The answer to \(\bf 1/2 \div 1/4\) is the answer to this question: How many 1/4's are contained in 1/2?
Let 1 unit = 2 rows of dots by 4 columns of dots:
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \]
Then represent the number 1/2 based on this unit, and the number 1/4 based on this unit.
1/2 = \( \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot}\end{matrix} \) and 1/4 = \(\begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix}\)
In the set representing 1/2, circle as many sets as possible that represent 1/4:
Count how many 1/4's are in 1/2. There are 2 1/4's in 1/2, so the answer is 2.
This can also be done using C-strips. Let the unit = N. Then 1/2 = P and 1/4 = R. Since there are 2 reds in the purple C-strip, 1/2 \(\div\) 1/4 = 2.
Use a model to do the following division: 1/5 \(\div\) 1/10. Use boxes, dots, or C-strips. First define the unit. Then explain and show all of the steps.
Perform the following division using each of the methods (boxes, dots, C-strips):
1/3 \(\div\) 1/9. First define the unit. Then explain and show all of the steps.
Perform the following division using each of the methods (boxes, dots, C-strips):
2/3 \(\div\) 1/6. First define the unit. Then explain and show all of the steps.
Perform the following division using each of the methods (boxes, dots, C-strips):
3 \(\div\) 1/4. First define the unit. Then explain and show all of the steps.


