33.4: Equivalent Exponential Expressions
- Page ID
- 40612
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson
Let's investigate expressions with variables and exponents.
Exercise \(\PageIndex{1}\): Up or Down?
Find the values of \(3^{x}\) and \(\left(\frac{1}{3}\right)^{x}\) for different values of \(x\). What patterns do you notice?
| \(x\) | \(3^{x}\) | \(\left(\frac{1}{3}\right)^{x}\) |
|---|---|---|
| \(1\) | ||
| \(2\) | ||
| \(3\) | ||
| \(4\) |
Exercise \(\PageIndex{2}\): What's the Value?
Evaluate each expression for the given value of \(x\).
- \(3x^{2}\) when \(x\) is \(10\)
- \(3x^{2}\) when \(x\) is \(\frac{1}{9}\)
- \(\frac{x^{3}}{4}\) when \(x\) is \(4\)
- \(\frac{x^{3}}{4}\) when \(x\) is \(\frac{1}{2}\)
- \(9+x^{7}\) when \(x\) is \(1\)
- \(9+x^{7}\) when \(x\) is \(\frac{1}{2}\)
Exercise \(\PageIndex{3}\): Exponent Experimentation
Find a solution to each equation in the list. (Numbers in the list may be a solution to more than one equation, and not all numbers in the list will be used.)
- \(64=x^{2}\)
- \(64=x^{3}\)
- \(2^{x}=32\)
- \(x=\left(\frac{2}{5}\right)^{3}\)
- \(\frac{16}{9}=x^{2}\)
- \(2\cdot 2^{5}=2^{x}\)
- \(2x=2^{4}\)
- \(4^{3}=8^{x}\)
List:
\(\frac{8}{125}\quad \frac{6}{15}\quad\frac{5}{8}\quad\frac{8}{9}\quad 1\frac{4}{3}\quad 2\quad 3\quad 4\quad 5\quad 6\quad 8\)
Are you ready for more?
This fractal is called a Sierpinski Tetrahedron. A tetrahedron is a polyhedron that has four faces. (The plural of tetrahedron is tetrahedra.)
The small tetrahedra form four medium-sized tetrahedra: blue, red, yellow, and green. The medium-sized tetrahedra form one large tetrahedron.

- How many small faces does this fractal have? Be sure to include faces you can’t see. Try to find a way to figure this out so that you don’t have to count every face.
- How many small tetrahedra are in the bottom layer, touching the table?
- To make an even bigger version of this fractal, you could take four fractals like the one pictured and put them together. Explain where you would attach the fractals to make a bigger tetrahedron.
- How many small faces would this bigger fractal have? How many small tetrahedra would be in the bottom layer?
- What other patterns can you find?
Summary
In this lesson, we saw expressions that used the letter \(x\) as a variable. We evaluated these expressions for different values of \(x\).
- To evaluate the expression \(2x^{3}\) when \(x\) is \(5\), we replace the letter \(x\) with \(5\) to get \(2\cdot 5^{3}\). This is equal to \(2\cdot 125\) or just \(250\). So the value of \(2x^{3}\) is \(250\) when \(x\) is \(5\).
- To evaluate \(\frac{x^{2}}{8}\) when \(x\) is \(4\), we replace the letter \(x\) with \(4\) to get \(\frac{4^{2}}{8}=\frac{16}{8}\), which equals \(2\). So \(\frac{x^{2}}{8}\) has a value of \(2\) when \(x\) is \(4\).
We also saw equations with the variable \(x\) and had to decide what value of \(x\) would make the equation true.
- Suppose we have an equation \(10\cdot 3^{x}=90\) and a list of possible solutions: \(1, 2, 3, 9, 11\). The only value of \(x\) that makes the equation true is \(2\) because \(10\cdot 3^{2}=10\cdot 3\cdot 3\), which equals \(90\). So \(2\) is the solution to the equation.
Practice
Exercise \(\PageIndex{4}\)
Evaluate each expression if \(x=3\).
- \(2^{x}\)
- \(x^{2}\)
- \(1^{x}\)
- \(x^{1}\)
- \(\left(\frac{1}{2}\right)^{x}\)
Exercise \(\PageIndex{5}\)
Evaluate each expression for the given value of each variable.
- \(2+x^{3}\), \(x\) is \(3\)
- \(x^{2}\), \(x\) is \(\frac{1}{2}\)
- \(3x^{2}+y\), \(x\) is \(5\) \(y\) is \(3\)
- \(10y+x^{2}\), \(x\) is \(6\) \(y\) is \(4\)
Exercise \(\PageIndex{6}\)
Decide if the expressions have the same value. If not, determine which expression has the larger value.
- \(2^{3}\) and \(3^{2}\)
- \(1^{31}\) and \(31^{1}\)
- \(4^{2}\) and \(2^{4}\)
- \(\left(\frac{1}{2}\right)^{3}\) and \(\left(\frac{1}{3}\right)^{2}\)
Exercise \(\PageIndex{7}\)
Match each equation to its solution.
- \(7+x^{2}=16\)
- \(5-x^{2}=1\)
- \(2\cdot 2^{3}=2^{x}\)
- \(\frac{3^{4}}{3^{x}}=27\)
- \(x=1\)
- \(x=2\)
- \(x=3\)
- \(x=4\)
Exercise \(\PageIndex{8}\)
An adult pass at the amusement park costs 1.6 times as much as a child’s pass.
- How many dollars does an adult pass cost if a child’s pass costs:
\($5\)?
\($10\)?
\(w\) dollars? - A child's pass costs $15. How many dollars does an adult pass cost?
(From Unit 6.2.1)
Exercise \(\PageIndex{9}\)
Jada reads 5 pages every 20 minutes. At this rate, how many pages can she read in 1 hour?
- Use a double number line to find the answer.
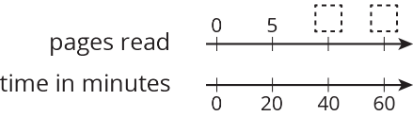
- Use a table to find the answer.
| pages read | time in minutes |
|---|---|
| \(5\) | \(20\) |
Which strategy do you think is better, and why?
(From Unit 2.4.4)

