33.3: Evaluating Expressions with Exponents

Last updated

Mar 27, 2022
Save as PDF
- 33.2: Expressions with Exponents
- 33.4: Equivalent Exponential Expressions

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's find the values of expressions with exponents.

Exercise $\PageIndex{1}$ : Revisiting the Cube

Based on the given information, what other measurements of the square and cube could we find?

Exercise $\PageIndex{2}$ : Calculating Surface Area

A cube has side length 10 inches. Jada says the surface area of the cube is 600 in², and Noah says the surface area of the cube is 3,600 in². Here is how each of them reasoned:

Jada’s Method:

$\begin{array}{l}{6\cdot 10^{2}}\\{6\cdot 100}\\{600}\end{array}$

Noah's Method:

$\begin{array}{l}{6\cdot 10^{2}}\\{60^{2}}\\{3,600}\end{array}$

Do you agree with either of them? Explain your reasoning.

Exercise $\PageIndex{3}$ : Row Game: Expression Explosion

Evaluate the expressions in one of the columns. Your partner will work on the other column. Check with your partner after you finish each row. Your answers in each row should be the same. If your answers aren’t the same, work together to find the error.

Table $\PageIndex{1}$
column A	column B
$5^{2}+4$	$2^{2}+25$
$2^{4}\cdot 5$	$2^{3}\cdot 10$
$3\cdot r^{2}$	$12\cdot 2^{2}$
$20+2^{3}$	$1+3^{3}$
$9\cdot 2^{1}$	$3\cdot 6^{1}$
$\frac{1}{9}\cdot\left(\frac{1}{2}\right)^{3}$	$\frac{1}{8}\cdot\left(\frac{1}{3}\right)^{2}$

Are you ready for more?

Consider this equation: 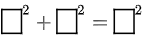$clipboard_e3aeff9b55b0d7d35c33b045029506d54.png$ . An example of 3 different whole numbers that could go in the boxes are 3, 4, and 5, since $3^{2}+4^{2}=5^{2}$ . (That is, $9+16=25$ .)
Can you find a different set of 3 whole numbers that make the equation true?
How many sets of 3 different whole numbers can you find?
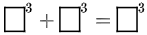
Can you find a set of 3 different whole numbers that make this equation true? $clipboard_efd81329735c241f727f05b5336c85803.png$
How about this one? $clipboard_eedeef842eb57fb8f2eeab7520ca1ce29.png$

Once you have worked on this a little while, you can understand a problem that is famous in the history of math. (Alas, this space is too small to contain it.) If you are interested, consider doing some further research on Fermat’s Last Theorem.

Summary

Exponents give us a new way to describe operations with numbers, so we need to understand how exponents get along with the other operations we know.

When we write $6\cdot 4^{2}$ , we want to make sure everyone agrees about how to evaluate this. Otherwise some people might multiply first and others compute the exponent first, and different people would get different values for the same expression!

Earlier we saw situations in which $6\cdot 4^{2}$ represented the surface area of a cube with side lengths 4 units. When computing the surface area, we evaluate $4^{2}$ first (or find the area of one face of the cube first) and then multiply the result by 6. In many other expressions that use exponents, the part with an exponent is intended to be evaluated first.

To make everyone agree about the value of expressions like $6\cdot 4^{2}$ , the convention is to evaluate the part of the expression with the exponent first. Here are a couple of examples:

$\begin{array}{cccc}{6\cdot 4^{2}}&{\qquad}&{\qquad}&{45+5^{2}}\\{6\cdot 16}&{\qquad}&{\qquad}&{45+25}\\ {96}&{\qquad}&{\qquad}&{70}\end{array}$

If we want to communicate that 6 and 4 should be multiplied first and then squared, then we can use parentheses to group parts together:

$\begin{array}{cccc}{(6\cdot 4)^{2}}&{\qquad}&{\qquad}&{(45+5)^{2}}\\{24^{2}}&{\qquad}&{\qquad}&{50^{2}}\\{576}&{\qquad}&{\qquad}&{2,500}\end{array}$

Practice

Exercise $\PageIndex{4}$

Lin says, “I took the number 8, and then multiplied it by the square of 3.” Select all the expressions that equal Lin’s answer.

$8\cdot 3^{2}$
$(8\cdot 3)^{2}$
$8\cdot 2^{3}$
$3^{2}\cdot 8$
$24^{2}$
$72$

Exercise $\PageIndex{5}$

Evaluate each expression.

$7+2^{3}$
$9\cdot 3^{1}$
$20-2^{4}$
$2\cdot 6^{2}$
$8\cdot\left(\frac{1}{2}\right)^{2}$
$\frac{1}{3}\cdot 3^{3}$
$\left(\frac{1}{5}\cdot 5\right)^{5}$

Exercise $\PageIndex{6}$

Andre says, “I multiplied 4 by 5, then cubed the result.” Select all the expressions that equal Andre’s answer.

$4\cdot 5^{3}$
$(4\cdot 5)^{3}$
$(4\cdot 5)^{2}$
$5^{3}\cdot 4$
$20^{3}$
$500$
$8,000$

Exercise $\PageIndex{7}$

Han has 10 cubes, each 5 inches on a side.

Find the total volume of Han’s cubes. Express your answer as an expression using an exponent.
Find the total surface area of Han’s cubes. Express your answer as an expression using an exponent.

Exercise $\PageIndex{8}$

Priya says that $\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}\cdot\frac{1}{3}=\frac{4}{3}$ . Do you agree with Priya? Explain or show your reasoning.

(From Unit 6.3.2)

Exercise $\PageIndex{9}$

Answer each question. Show your reasoning.

$125$ % of $e$ is $30$ . What is $e$ ?
$35$ % of $f$ is $14$ . What is $f$ ?

(From Unit 6.2.2)

Exercise $\PageIndex{10}$

Which expressions are solutions to the equation $2.4y=13.75$ ? Select all that apply.

$13.75-1.4$
$13.75\cdot 2.4$
$13.75\div 2.4$
$\frac{13.75}{2.4}$
$2.4\div 13.75$

(From Unit 6.1.5)

Exercise $\PageIndex{11}$

Jada explains how she finds $15\cdot 23$ :

“I know that ten 23s is 230, so five 23s will be half of 230, which is 115.
15 is 10 plus 5, so $15\cdot 23$ is 230 plus 115, which is 345.”

Do you agree with Jada? Explain.
Draw a 15 by 23 rectangle. Partition the rectangle into two rectangles and label them to show Jada’s reasoning.

(From Unit 5.3.3)

Search

Text Color

Text Size

Margin Size

Font Type

Lesson

Summary

Practice

Support Center

How can we help?