33.1: Meaning of Exponents

Lesson

Let's see how exponents show repeated multiplication.

Exercise \(\PageIndex{1}\): Notice and Wonder: Dots and Lines

What do you notice? What do you wonder?

Figure \(\PageIndex{1}\): A figure of a series of dot branches. In the center is a black dot. Three branches extend from the black dot with one red dot at the end of each branch. There are three branches that extend from each red dot with one green dot at the end of each branch. There are three branches that extend from each green dot with one yellow dot at the end of each branch. There are three branches that extend from each yellow dot with one blue dot at the end of each branch.

Exercise \(\PageIndex{2}\): The Genie's Offer

You find a brass bottle that looks really old. When you rub some dirt off of the bottle, a genie appears! The genie offers you a reward. You must choose one:

• $50,000; or
• A magical $1 coin. The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.

1. The number of coins on the third day will be \(2\cdot 2\cdot 2\). Write an equivalent expression using exponents.
2. What do \(2^{5}\) and \(2^{6}\) represent in this situation? Evaluate \(2^{5}\) and \(2^{6}\) without a calculator.
3. How many days would it take for the number of magical coins to exceed $50,000?
4. Will the value of the magical coins exceed a million dollars within the 28 days? Explain or show your reasoning.

Explore the applet. (Why do you think it stops?)

Are you ready for more?

A scientist is growing a colony of bacteria in a petri dish. She knows that the bacteria are growing and that the number of bacteria doubles every hour.

When she leaves the lab at 5 p.m., there are 100 bacteria in the dish. When she comes back the next morning at 9 a.m., the dish is completely full of bacteria. At what time was the dish half full?

Exercise \(\PageIndex{3}\): Make 81

1. Here are some expressions. All but one of them equals 16. Find the one that is not equal to 16 and explain how you know.

\(2^{3}\cdot 2\qquad 4^{2}\qquad\frac{2^{5}}{2}\qquad 8^{2}\)

2. Write three expressions containing exponents so that each expression equals 81.

Summary

When we write an expression like \(2^{n}\), we call \(n\) the exponent.

If \(n\) is a positive whole number, it tells how many factors of 2 we should multiply to find the value of the expression. For example, \(2^{1}=2\), and \(2^{5}=2\cdot 2\cdot 2\cdot 2\cdot 2\).

There are different ways to say \(2^{5}\). We can say “two raised to the power of five” or “two to the fifth power” or just “two to the fifth.”

Practice

Exercise \(\PageIndex{4}\)

Select all the expressions that are equivalent to \(64\).

1. \(2^{6}\)
2. \(2^{8}\)
3. \(4^{3}\)
4. \(8^{2}\)
5. \(16^{4}\)
6. \(32^{2}\)

Exercise \(\PageIndex{5}\)

Select all the expressions that equal \(3^{4}\).

1. \(7\)
2. \(4^{3}\)
3. \(12\)
4. \(81\)
5. \(64\)
6. \(9^{2}\)

Exercise \(\PageIndex{6}\)

\(4^{5}\) is equal to 1,024. Evaluate each expression.

1. \(4^{6}\)
2. \(4^{4}\)
3. \(4^{3}\cdot 4^{2}\)

Exercise \(\PageIndex{7}\)

\(6^{3}=216\). Using exponents, write three more expressions whose value is \(216\).

Exercise \(\PageIndex{8}\)

Find two different ways to rewrite \(3xy+6yz\) using the distributive property.

(From Unit 6.2.6)

Exercise \(\PageIndex{9}\)

Solve each equation.

\(a-2.01=5.5\)

\(b+2.01=5.5\)

\(10c=13.71\)

\(100d=13.71\)

(From Unit 6.1.5)

Exercise \(\PageIndex{10}\)

Which expressions represent the total area of the large rectangle? Select all that apply.

Figure \(\PageIndex{2}\)

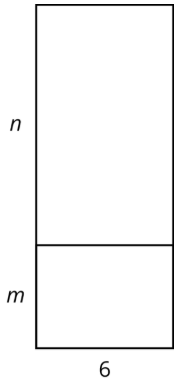
1. \(6(m+n)\)
2. \(6n+m\)
3. \(6n+6m\)
4. \(6mn\)
5. \((n+m)6\)

(From Unit 6.2.5)

Exercise \(\PageIndex{11}\)

Is each statement true or false? Explain your reasoning.

1. \(\frac{45}{100}\cdot 72=\frac{45}{72}\cdot 100\)
2. \(16\)% of \(250\) is equal to \(250\)% of \(16\)

(From Unit 3.4.7)