1.2: Introduction to Whole Numbers (Part 2)

Last updated
Save as PDF

Page ID: 5260

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Round Whole Numbers

In 2013, the U.S. Census Bureau reported the population of the state of New York as $19,651,127$ people. It might be enough to say that the population is approximately $20$ million. The word approximately means that $20$ million is not the exact population, but is close to the exact value.

The process of approximating a number is called rounding. Numbers are rounded to a specific place value depending on how much accuracy is needed. $20$ million was achieved by rounding to the millions place. Had we rounded to the one hundred thousands place, we would have $19,700,000$ as a result. Had we rounded to the ten thousands place, we would have $19,650,000$ as a result, and so on. The place value to which we round to depends on how we need to use the number.

Using the number line can help you visualize and understand the rounding process. Look at the number line in Figure $\PageIndex{10}$. Suppose we want to round the number $76$ to the nearest ten. Is $76$ closer to $70$ or $80$ on the number line?

$An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “76” on the number line.$

Figure $\PageIndex{10}$: We can see that $76$ is closer to $80$ than to $70$. So $76$ rounded to the nearest ten is $80$.

Now consider the number $72$. Find $72$ in Figure $\PageIndex{11}$.

$An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “72” on the number line.$

Figure $\PageIndex{11}$: We can see that $72$ is closer to $70$, so $72$ rounded to the nearest ten is $70$.

How do we round $75$ to the nearest ten. Find $75$ in Figure $\PageIndex{12}$.

$An image of a number line from 70 to 80 with increments of one. All the numbers on the number line are black except for 70 and 80 which are red. There is an orange dot at the value “75” on the number line.$

Figure $\PageIndex{12}$: The number $75$ is exactly midway between $70$ and $80$.

So that everyone rounds the same way in cases like this, mathematicians have agreed to round to the higher number, $80$. So, $75$ rounded to the nearest ten is $80$.

Now that we have looked at this process on the number line, we can introduce a more general procedure. To round a number to a specific place, look at the number to the right of that place. If the number is less than $5$, round down. If it is greater than or equal to $5$, round up.

So, for example, to round $76$ to the nearest ten, we look at the digit in the ones place.

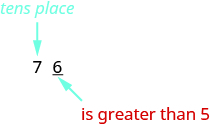
$An image of value “76”. The text “tens place” is in blue and points to number 7 in “76”. The text “is greater than 5” is in red and points to the number 6 in “76”.$

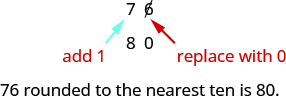
The digit in the ones place is a $6$. Because $6$ is greater than or equal to $5$, we increase the digit in the tens place by one. So the $7$ in the tens place becomes an $8$. Now, replace any digits to the right of the $8$ with zeros. So, $76$ rounds to $80$.

$An image of the value “76”. The “6” in “76” is crossed out and has an arrow pointing to it which says “replace with 0”. The “7” has an arrow pointing to it that says “add 1”. Under the value “76” is the value “80”.$

Let’s look again at rounding $72$ to the nearest $10$. Again, we look to the ones place.

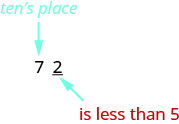
$An image of value “72”. The text “tens place” is in blue and points to number 7 in “72”. The text “is less than 5” is in red and points to the number 2 in “72”.$

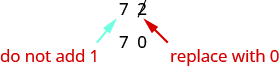
The digit in the ones place is $2$. Because $2$ is less than $5$, we keep the digit in the tens place the same and replace the digits to the right of it with zero. So $72$ rounded to the nearest ten is $70$.

$An image of the value “72”. The “2” in “72” is crossed out and has an arrow pointing to it which says “replace with 0”. The “7” has an arrow pointing to it that says “do not add 1”. Under the value “72” is the value “70”.$

How to: Round a Whole Number to a Specific Place Value

Step 1. Locate the given place value. All digits to the left of that place value do not change.

Step 2. Underline the digit to the right of the given place value.

Step 3. Determine if this digit is greater than or equal to $5$.

Yes—add $1$ to the digit in the given place value.
No—do not change the digit in the given place value.

Step 4. Replace all digits to the right of the given place value with zeros.

Example $\PageIndex{8}$: round a whole number

Round $843$ to the nearest ten.

Solution

Locate the tens place.	$CNX_BMath_Figure_01_01_034_img-01.png$
Underline the digit to the right of the tens place.	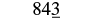$CNX_BMath_Figure_01_01_034_img-02.png$
Since 3 is less than 5, do not change the digit in the tens place.	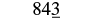$CNX_BMath_Figure_01_01_034_img-02.png$
Replace all digits to the right of the tens place with zeros.	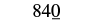$CNX_BMath_Figure_01_01_034_img-04.png$
	Rounding 843 to the nearest ten gives 840.

Exercise $\PageIndex{15}$

Round to the nearest ten: $157$

Answer: $160$

Exercise $\PageIndex{16}$

Round to the nearest ten: $884$

Answer: $880$

Example $\PageIndex{9}$: round a whole number

Round each number to the nearest hundred:

$23,658$
$3,978$

Solution

Locate the hundreds place.	$..$
The digit of the right of the hundreds place is 5. Underline the digit to the right of the hundreds place.	$..$
Since 5 is greater than or equal to 5, round up by adding 1 to the digit in the hundreds place. Then replace all digits to the right of the hundreds place with zeros.	$..$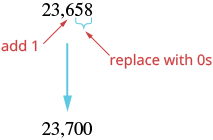
	So 23,658 rounded to the nearest hundred is 23,700.

Locate the hundreds place.	$..$
Underline the digit to the right of the hundreds place.	$..$
The digit to the right of the hundreds place is 7. Since 7 is greater than or equal to 5, round up by added 1 to the 9. Then replace all digits to the right of the hundreds place with zeros.	$..$
	So 3,978 rounded to the nearest hundred is 4,000.

Exercise $\PageIndex{17}$

Round to the nearest hundred: $17,852$.

Answer: $17,900$

Exercise $\PageIndex{18}$

Round to the nearest hundred: $4,951$.

Answer: $5,000$

Example $\PageIndex{10}$: Round a whole number

Round each number to the nearest thousand:

$147,032$
$29,504$

Solution

Locate the thousands place. Underline the digit to the right of the thousands place.	$..$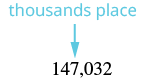
The digit to the right of the thousands place is 0. Since 0 is less than 5, we do not change the digit in the thousands place.	$..$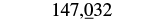
We then replace all digits to the right of the thousands pace with zeros.	$..$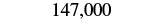
	So 147,032 rounded to the nearest thousand is 147,000.

Locate the thousands place.	$..$
Underline the digit to the right of the thousands place.	$..$
The digit to the right of the thousands place is 5. Since 5 is greater than or equal to 5, round up by adding 1 to the 9. Then replace all digits to the right of the thousands place with zeros.	$..$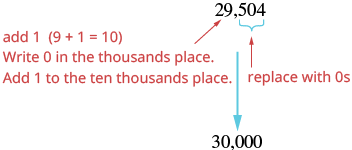
	So 29,504 rounded to the nearest thousand is 30,000.

Notice that in part (b), when we add $1$ thousand to the $9$ thousands, the total is $10$ thousands. We regroup this as $1$ ten thousand and $0$ thousands. We add the $1$ ten thousand to the $2$ ten thousands and put a $0$ in the thousands place.

Exercise $\PageIndex{19}$

Round to the nearest thousand: $63,921$.

Answer: $64,000$

Exercise $\PageIndex{20}$

Round to the nearest thousand: $156,437$.

Answer: $156,000$

Access Additional Online Resources

Write a Whole Number in Digits from Words

Key Concepts

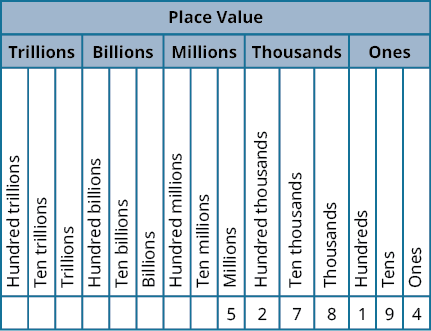
$A chart titled 'Place Value' with fifteen columns and 4 rows, with the columns broken down into five groups of three. The header row shows Trillions, Billions, Millions, Thousands, and Ones. The next row has the values 'Hundred trillions', 'Ten trillions', 'trillions', 'hundred billions', 'ten billions', 'billions', 'hundred millions', 'ten millions', 'millions', 'hundred thousands', 'ten thousands', 'thousands', 'hundreds', 'tens', and 'ones'. The first 8 values in the next row are blank. Starting with the ninth column, the values are '5', '2', '7', '8', '1', '9', and '4'.$

Figure $\PageIndex{13}$

Name a whole number in words.
- Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.
- Use commas in the number to separate the periods.
Use place value to write a whole number.
- Identify the words that indicate periods. (Remember the ones period is never named.)
- Draw three blanks to indicate the number of places needed in each period.
- Name the number in each period and place the digits in the correct place value position.
Round a whole number to a specific place value.
- Locate the given place value. All digits to the left of that place value do not change.
- Underline the digit to the right of the given place value.
- Determine if this digit is greater than or equal to $5$. If yes—add $1$ to the digit in the given place value. If no—do not change the digit in the given place value.
- Replace all digits to the right of the given place value with zeros.

Glossary

coordinate: A number paired with a point on a number line is called the coordinate of the point.
counting numbers: The counting numbers are the numbers 1, 2, 3, ….
number line: A number line is used to visualize numbers. The numbers on the number line get larger as they go from left to right, and smaller as they go from right to left.
origin: The origin is the point labeled 0 on a number line.
place value system: Our number system is called a place value system because the value of a digit depends on its position, or place, in a number.
rounding: The process of approximating a number is called rounding.
whole numbers: The whole numbers are the numbers 0, 1, 2, 3, ….

Practice Problems

Identify Counting Numbers and Whole Numbers

In the following exercises, determine which of the following numbers are (a) counting numbers (b) whole numbers.

0, $\dfrac{2}{3}$, 5, 8.1, 125
0, $\dfrac{7}{10}$, 3, 20.5, 300
0, $\dfrac{4}{9}$, 3.9, 50, 221
0, $\dfrac{3}{5}$, 10, 303, 422.6

Model Whole Numbers

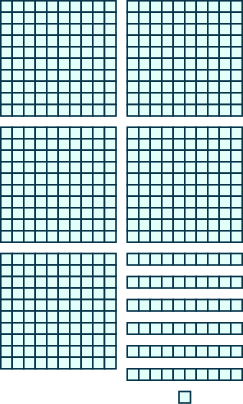
In the following exercises, use place value notation to find the value of the number modeled by the base-10 blocks.

$An image consisting of three items. The first item is five squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is six horizontal rods containing 10 blocks each. The third item is 1 individual block.$

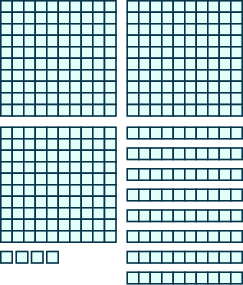
$An image consisting of three items. The first item is three squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is eight horizontal rods containing 10 blocks each. The third item is 4 individual blocks.$

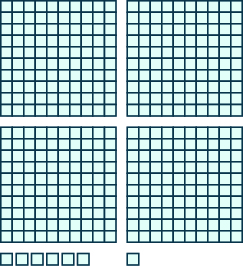
$An image consisting of two items. The first item is four squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is 7 individual blocks.$

$An image consisting of two items. The first item is six squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is 2 horizontal rods with 10 blocks each.$

Identify the Place Value of a Digit

In the following exercises, find the place value of the given digits.

579,601

(a) 9 (b) 6 (c) 0 (d) 7 (e) 5

398,127

(a) 9 (b) 3 (c) 2 (d) 8 (e) 7

56,804,379

(a) 8 (b) 6 (c) 4 (d) 7 (e) 0

78,320,465

(a) 8 (b) 4 (c) 2 (d) 6 (e) 7

Use Place Value to Name Whole Numbers

In the following exercises, name each number in words.

1,078
5,902
364,510
146,023
5,846,103
1,458,398
37,889,005
62,008,465
The height of Mount Ranier is 14,410 feet.
The height of Mount Adams is 12,276 feet.
Seventy years is 613,200 hours.
One year is 525,600 minutes.
The U.S. Census estimate of the population of Miami-Dade county was 2,617,176.
The population of Chicago was 2,718,782.
There are projected to be 23,867,000 college and university students in the US in five years.
About twelve years ago there were 20,665,415 registered automobiles in California.
The population of China is expected to reach 1,377,583,156 in 2016.
The population of India is estimated at 1,267,401,849 as of July 1, 2014.

Use Place Value to Write Whole Numbers

In the following exercises, write each number as a whole number using digits.

four hundred twelve
two hundred fifty-three
thirty-five thousand, nine hundred seventy-five
sixty-one thousand, four hundred fifteen
eleven million, forty-four thousand, one hundred sixty-seven
eighteen million, one hundred two thousand, seven hundred eighty-three
three billion, two hundred twenty-six million, five hundred twelve thousand, seventeen
eleven billion, four hundred seventy-one million, thirty-six thousand, one hundred six
The population of the world was estimated to be seven billion, one hundred seventy-three million people.
The age of the solar system is estimated to be four billion, five hundred sixty-eight million years.
Lake Tahoe has a capacity of thirty-nine trillion gallons of water.
The federal government budget was three trillion, five hundred billion dollars.

Round Whole Numbers

In the following exercises, round to the indicated place value.

Round to the nearest ten:

(a) 386 (b) 2,931

Round to the nearest ten:

(a) 792 (b) 5,647

Round to the nearest hundred:

(a) 13,748 (b) 391,794

Round to the nearest hundred:

(a) 28,166 (b) 481,628

Round to the nearest ten:

(a) 1,492 (b) 1,497

Round to the nearest thousand:

(a) 2,391 (b) 2,795

Round to the nearest hundred:

(a) 63,994 (b) 63,949

Round to the nearest thousand:

(a) 163,584 (b) 163,246

Everyday Math

Writing a Check Jorge bought a car for $24,493. He paid for the car with a check. Write the purchase price in words.
Writing a Check Marissa’s kitchen remodeling cost $18,549. She wrote a check to the contractor. Write the amount paid in words.
Buying a Car Jorge bought a car for $24,493. Round the price to the nearest:

(a) ten dollars (b) hundred dollars (c) thousand dollars (d) ten-thousand dollars

Remodeling a Kitchen Marissa’s kitchen remodeling cost $18,549. Round the cost to the nearest:

(a) ten dollars (b) hundred dollars (c) thousand dollars (d) ten-thousand dollars

Population The population of China was 1,355,692,544 in 2014. Round the population to the nearest:

(a) billion people (b) hundred-million people (c) million people

Astronomy The average distance between Earth and the sun is 149,597,888 kilometers. Round the distance to the nearest:

(a) hundred-million kilometers (b) ten-million kilometers (c) million kilometers

Writing Exercises

In your own words, explain the difference between the counting numbers and the whole numbers.
Give an example from your everyday life where it helps to round numbers.

Self Check

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$.$

(b) If most of your checks were...

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.

Search

Text Color

Text Size

Margin Size

Font Type

How to: Round a Whole Number to a Specific Place Value

Example \(\PageIndex{8}\): round a whole number

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Example \(\PageIndex{9}\): round a whole number

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Example \(\PageIndex{10}\): Round a whole number

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)