Skip to main content
Library homepage
 

Text Color

Text Size

 

Margin Size

 

Font Type

Enable Dyslexic Font
Mathematics LibreTexts

1.E: Applications of Limits (Exercises)

  1. CCBYNC
  2. Last updated
    Dec 21, 2020
  3. Save as PDF

( \newcommand{\kernel}{\mathrm{null}\,}\)

1.1: An Introduction to Limits

Terms and Concepts

  1. In your own words, what does it mean to "find the limit of f⁡(x) as x approaches 3"?
  2. An expression of the form 00 is called _____.
  3. T/F: The limit of f⁡(x) as x approaches 5 is f⁡(5).
  4. Describe three situations where limx→c⁡f⁡(x) does not exist.
  5. In your own words, what is a difference quotient.

Problems

In Exercises 6-16, approximate the given limits both numerically and graphically.

6. limx→1⁡x2+3⁢x−5

7. limx→0⁡x3−3⁢x2+x−5

8. limx→0⁡x+1x2+3⁢x

9. limx→3⁡x2−2⁢x−3x2−4⁢x+3

10. limx→−1⁡x2+8⁢x+7x2+6⁢x+5

11. limx→2⁡x2+7⁢x+10x2−4⁢x+4

12. limx→2, where f⁡(x)={x+2x≤23⁢x−5x>2.

13. limx→3, where f⁡(x)={x2−x+1x≤32⁢x+1x>3.

14. limx→0, where f⁡(x)={cos⁡xx≤0x2+3⁢x+1x>0.

15. limx→π/2, where f⁡(x)={sin⁡xx≤π/2cos⁡xx>π/2.

In Exercises 16-24, a function f and a value a are given. Approximate the limit of the difference quotient, limh→0⁡f⁡(a+h)−f⁡(a)h, using h=±0.1,±0.01.

16. f⁡(x)=−7⁢x+2,a=3

17. f⁡(x)=9⁢x+0.06,a=−1

18. f⁡(x)=x2+3⁢x−7,a=1

19. f⁡(x)=1x+1,a=2

20. f⁡(x)=−4⁢x2+5⁢x−1,a=−3

21. f⁡(x)=ln⁡x,a=5

22. f⁡(x)=sin⁡x,a=π

23. f⁡(x)=cos⁡x,a=π

1.2: Epsilon-Delta Definition of a Limit

Terms and Concepts

1. What is wrong with the following "definition" of a limit?

"The limit of f⁡(x), as x approaches a, is K″ means that given any δ>0 there exists ϵ>0 such that whenever |f⁡(x)−K|<ϵ, we have |x−a|<δ.

2. Which is given first in establishing a limit, the x-tolerance or the y-tolerance?

3. T/F: ϵ must always be positive.

4. T/F: δ must always be positive.

Problems

In Exercises 5-11, prove the given limit using an ϵ−δ proof.

5. limx→5⁡3−x+−2

6. limx→3⁡x2−3=6

7. limx→4⁡x2+x−5=15

8. limx→2⁡x3−1=7

9. limx→2⁡5=5

10. limx→0⁡e2⁢x−1=0

11. limx→0⁡sin⁡x=0 (Hint: use the fact that |sin⁡x|≤|x|, with equality only when x=0.)

1.3: Finding Limits Analytically

Terms and Concepts

1. Explain in your own words, without using ε−δ formality, why limx→c⁡b=b.

2. Explain in your own words, without using ε−δ formality, why limx→c⁡x=c.

3. What does the text mean when it says that certain functions’ “behavior is ‘nice’ in terms of limits”? What, in particular, is “nice”?

4. Sketch a graph that visually demonstrates the Squeeze Theorem.

5. You are given the following information:

(a) limx→1⁡f⁡(x)=0

(b) limx→1⁡g⁡(x)=0

(c) limx→1⁡f⁡(x)/g⁡(x)=2

What can be said about the relative sizes of f⁡(x) and g⁡(x) as x approaches 1?

Problems

Using:

(1.E.1)limx→9⁡f⁡(x)=6limx→6⁡f⁡(x)=9(1.E.2)limx→9⁡g⁡(x)=3limx→6⁡g⁡(x)=3

evaluate the limits given in Exercises 6-13, where possible. If it is not possible to know, state so.

6. limx→9⁡(f⁡(x)+g⁡(x))

7. limx→9⁡(3⁢f⁡(x)/g⁡(x))

8. limx→9⁡(f⁡(x)−2⁢g⁡(x)g⁡(x))

9. limx→6⁡(f⁡(x)3−g⁡(x))

10. limx→9⁡g⁡(f⁡(x))

11. limx→6⁡f⁡(g⁡(x))

12. limx→6⁡g⁡(f⁡(f⁡(x)))

13. limx→6⁡f⁡(x)⁢g⁡(x)−f2⁡(x)+g2⁡(x)

Using

(1.E.3)limx→1⁡f⁡(x)=2limx→10⁡f⁡(x)=1(1.E.4)limx→1⁡g⁡(x)=0limx→10⁡g⁡(x)=π

evaluate the limits given in Exercises 14-17, where possible. If it is not possible to know, state so.

14. limx→1⁡f⁡(x)g⁡(x)

15. limx→10⁡cos⁡(g⁡(x))

16. limx→1⁡f⁡(x)⁢g⁡(x)

17. limx→1⁡g⁡(5⁢f⁡(x))

In Exercises 18-32, evaluate the given limit.

18. limx→3⁡x2−3⁢x+7

19. limx→π⁡(x−3x+5)7

20. limx→π/4⁡cos⁡x⁢sin⁡x

21. limx→0⁡ln⁡x

22. limx→3⁡4x3−8⁢x

23. limx→π/6⁡csc⁡x

24. limx→0⁡ln⁡(1+x)

25. limx→π⁡x2+3⁢x+55⁢x2−2⁢x−3

26.limx→π⁡3⁢x+11−x

27.limx→6⁡x2−4⁢x−12x2−13⁢x+42

28.limx→0⁡x2+2⁢xx2−2⁢x

29.limx→2⁡x2+6⁢x−16x2−3⁢x+2

30.limx→2⁡x2−5⁢x−14x2+10⁢x+16

31.limx→−2⁡x2−5⁢x−14x2+10⁢x+16

32.limx→−1⁡x2+9⁢x+8x2−6⁢x−7\

Use the Squeeze Theorem in Exercises 33-36, where appropriate, to evaluate the given limit.

33. limx→0⁡x⁢sin⁡(1x)

34. limx→0⁡sin⁡x⁢cos⁡(1x2)

35. limx→1⁡f⁡(x), where 3⁢x−2≤f⁡(x)≤x3.

36. limx→3+⁡f⁡(x), where 6⁢x−9≤f⁡(x)≤x2 on [0,3].

Exercises 37-40, challenge your understanding of limits but can be evaluated using the knowledge gained in this section.

37. limx→0⁡sin⁡3⁢xx

38. limx→0⁡sin⁡5⁢x8⁢x

39. limx→0⁡ln⁡(1+x)x

40. limx→0⁡sin⁡xx, where x is measured in degrees not radians.

1.4: One Sided Limits

Terms and Concepts

1. What are the three ways in which a limit may fail to exist?

2. T/F: If limx→1−⁡f⁡(x)=5, then limx→1⁡f⁡(x)=5

3. T/F: If limx→1−⁡f⁡(x)=5, then limx→1+⁡f⁡(x)=5

4. T/F: If limx→1⁡f⁡(x)=5, then limx→1−⁡f⁡(x)=5

Problems

In Exercises 5-12, evaluate each expression using the given graph of f⁡(x).

5.
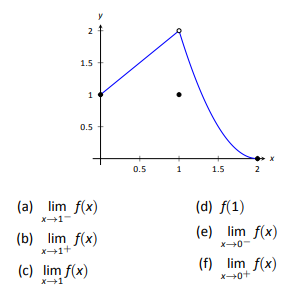
clipboard_e4f5a8bce92d31a43cde475d21c7bbb8f.png

6.
146.PNG

7.
147.PNG

8.
148.PNG

9.
149.PNG

10.
1410.PNG

11.
1411.PNG

12.
1412.PNG

In Exercises 13-21, evaluate the given limits of the piecewise defined functions f.

13. f⁡(x)={x+1x≤1x2−5x>1
(a) limx→1−⁡f⁡(x)
(b) limx→0+⁡f⁡(x)
(c) limx→1⁡f⁡(x)
(d) f⁡(1)

14. f⁡(x)={2⁢x2+5⁢x−1x<0sin⁡xx≥0
(a) limx→0−⁡f⁡(x)
(b) limx→0+⁡f⁡(x)
(c) limx→0⁡f⁡(x)
(d) f⁡(0)

15. f⁡(x)={x−⁢1x<−1x3+1−1≤x≤1x2+1x>1
(a) limx→−1−⁡f⁡(x)
(b) limx→1+⁡f⁡(x)
(c) limx→−1⁡f⁡(x)
(d) f⁡(−1)
(e) limx→1−⁡f⁡(x)
(f) limx→1+⁡f⁡(x)
(g) limx→1⁡f⁡(x)
(h) f⁡(1)

16. f⁡(x)={cos⁡xx<πsin⁡xx≥π
(a) limx→π−⁡f⁡(x)
(b) limx→π+⁡f⁡(x)
(c) limx→π⁡f⁡(x)
(d) f⁡(π)

17. f⁡(x)={1−cos2⁡xx<asin2⁡xx≥a, where a is a real number.
(a) limx→a−⁡f⁡(x)
(b) limx→a+⁡f⁡(x)
(c) limx→a⁡f⁡(x)
(d) f⁡(a)

18. f⁡(x)={x+1x<11x=1x−1x>1
(a) limx→1−⁡f⁡(x)
(b) limx→1+⁡f⁡(x)
(c) limx→1⁡f⁡(x)
(d) f⁡(1)

19. f⁡(x)={x2x<2x+1x=2−x2+2⁢x+4x>2
(a) limx→2−⁡f⁡(x)
(b) limx→2+⁡f⁡(x)
(c) limx→2⁡f⁡(x)
(d) f⁡(2)

20. f⁡(x)={a⁢(x−b)2+cx<ba⁢(x−b)+cx≥b, where a, b and c are real numbers.
(a) limx→b−⁡f⁡(x)
(b) limx→b+⁡f⁡(x)
(c) limx→b⁡f⁡(x)
(d) f⁡(b)

21. f⁡(x)={|x|xx≠00x=0
(a) limx→0−⁡f⁡(x)
(b) limx→0+⁡f⁡(x)
(c) limx→0⁡f⁡(x)
(d) f⁡(0)

Review

22. Evaluate the limit: limx→−1⁡x2+5⁢x+4x2−3⁢x−4

23. Evaluate the limit: limx→−4⁡x2−16x2−4⁢x−32

24. Evaluate the limit: limx→−6⁡x2−15⁢x+54x2−6⁢x

25. Approximate the limit numerically: limx→0.4⁡x2−4.4⁢x+1.6x2−0.4⁢x

26. Approximate the limit numerically: limx→0.2⁡x2+5.8⁢x−1.2x2−4.2⁢x+0.8

1.5: Continuity

Terms and Concepts

1. In your own words, describe what it means for a function to be continuous.

2. In your own words, describe what the Intermediate Value Theorem states.

3. What is a “root” of a function?

4. Given functions f and g on an interval I, how can the Bisection Method be used to find a value c where f⁡(c)=g⁡(c)?

5. T/F: If f is defined on an open interval containing c, and limx→c⁡f⁡(x) exists, then f is continuous at c.

6. T/F: If f is continuous at c, then limx→c⁡f⁡(x) exists

7. T/F: If f is continuous at c, then limx→c+⁡f⁡(x)=f⁡(c).

8. T/F: If f is continuous on [a, b], then limx→a−⁡f⁡(x)=f⁡(a).

9. T/F: If f is continuous on [0, 1) and [1, 2), then f is continuous on [0, 2).

10. T/F: The sum of continuous functions is also continuous.

Problems

In Exercises 11-17, a graph of a function f is given along with a value a. Determine if f is continuous at a; if it is not, state why it is not.

11. a=1
1511.PNG

12. a=1
1512.PNG

13. a=1
1513.PNG

14. a=0
1514.PNG

15. a=1
1515.PNG

16. a=4
1516.PNG

17.
(a) a=−2
(b) a=0
(c) a=2
1517.PNG

In Exercises 18-21, determine if f is continuous at the indicated values. If not, explain why.

18. f⁡(x)={1x=0sin⁡xxx>0
(a) x=0
(b) x=π

19. f⁡(x)={x3−xx<1x−2x≥1
(a) x=0
(b) x=1

20. f⁡(x)={x2+5⁢x+4x2+3⁢x+2x≠−13x=−1
(a) x=−1
(b) x=10

21. f⁡(x)={x2−64x2−11⁢x+24x≠85x=8
(a) x=0
(b) x=8

In Exercises 22-32, give the intervals on which the given function is continuous.

22. f⁡(x)=x2−3⁢x+9

23. g⁡(x)=x2−4

24. h⁡(k)=1−k+k+1

25. f⁡(t)=5⁢t2−30

26. g⁡(t)=11−t2

27. g⁡(x)=11+x2

28. f⁡(x)=ex

29. g⁡(s)=ln⁡s

30. h⁡(t)=cos⁡t

31. f⁡(k)=1−ek

32. f⁡(x)=sin⁡(ex+x2)

33. Let f be continuous on [1,5] where f⁡(1)=−2 and f⁡(5)=−10. Does a value 1<c<5 exist such that f⁡(c)=−9? Why/why not?

34. Let g be continuous on [-3,7] where g⁡(0)=0 and g⁡(2)=25. Does a value −3<c<7 exist such that g⁡(c)=15? Why/why not?

35. Let f be continuous on [-1,1] where f⁡(−1)=−10 and f⁡(1)=10. Does a value −1<c<1 exist such that f⁡(c)=11? Why/why not?

36. Let h be continuous on [-1,1] where h⁡(−1)=−10 and h⁡(1)=10. Does a value −1<c<1 exist such that h⁡(c)=0? Why/why not?

In Exercises 37-40, use the Bisection Method to approximate, accurate to two decimal places, the value of the root of the given function in the given interval.

37. f⁡(x)=x2+2⁢x−4 on [1,1.5].

38. f⁡(x)=sin⁡x−1/2 on [0.5,0.55].

39. f⁡(x)=ex−2 on [0.65,0.7].

40. f⁡(x)=cos⁡x−sin⁡x on [0.7,0.8].

Review

41. Let f⁡(x)={x2−5x<55⁢xx≥5.
(a) limx→5−⁡f⁡(x)
(b) limx→5+⁡f⁡(x)
(c) limx→5⁡f⁡(x)
(d) f⁡(5)

42. Numerically approximate the following limits:
(a) limx→4/5+⁡x2−8.2⁢x−7.2x2+5.8⁢x+4
(b) limx→4/5−⁡x2−8.2⁢x−7.2x2+5.8⁢x+4

43. Give an example of function f⁡(x) for which limx→0⁡f⁡(x) does not exist.

1.6: Limits Involving Infinity

Terms and Concepts

1. T/F: If limx→5⁡f⁡(x)=∞, then we are implicitly stating that the limit exists.

2. T/F: If limx→∞⁡f⁡(x)=5, then we are implicitly stating that the limit exists.

3. T/F: If limx→1−⁡f⁡(x)=−∞, then limx→1+⁡f⁡(x)=∞.

4. T/F: If limx→5⁡f⁡(x)=∞, then f has a vertical asymptote at x=5.

5. T/F: ∞/0 is not an indeterminate form.

6. List 5 indeterminate forms.

7. Construct a function with a vertical asymptote at x = 5 and a horizontal asymptote at y = 5.

8. Let limx→7⁡f⁡(x)=∞. Explain how we know that f is/is not continuous at x=7.

Problems

In Exercises 9-14, evaluate the given limits using the graph of the function.

9. f⁡(x)=1(x+1)2
(a) limx→−1−⁡f⁡(x)
(b) limx→−1+⁡f⁡(x)
169.PNG

10. f⁡(x)=1(x−3)⁢(x−5)2
(a) limx→3−⁡f⁡(x)
(b) limx→3+⁡f⁡(x)
(c) limx→3⁡f⁡(x)
(d) limx→5−⁡f⁡(x)
(e) limx→5+⁡f⁡(x)
(f) limx→5⁡f⁡(x)
1610.PNG

11. f⁡(x)=1ex+1
(a) limx→−∞⁡f⁡(x)
(b) limx→∞⁡f⁡(x)
(c) limx→0−⁡f⁡(x)
(d) limx→0+⁡f⁡(x)
1611.PNG

12. f⁡(x)=x2⁢sin⁡(π⁢x)
(a) limx→−∞⁡f⁡(x)
(b) limx→∞⁡f⁡(x)
1612.PNG

13. f⁡(x)=cos⁡(x)
(a) limx→−∞⁡f⁡(x)
(b) limx→∞⁡f⁡(x)
1613.PNG

14. f⁡(x)=2x+10
(a) limx→−∞⁡f⁡(x)
(b) limx→∞⁡f⁡(x)
1614.PNG

In Exercises 15-18, numerically approximate the following limits:
(a) limx→3−⁡f⁡(x)
(b) limx→3+⁡f⁡(x)
(c) limx→3⁡f⁡(x)

15. f⁡(x)=x2−1x2−x−6

16. f⁡(x)=x2+5⁢x−36x3−5⁢x2+3⁢x+9

17. f⁡(x)=x2−11⁢x+30x3−4⁢x2−3⁢x+18

18. f⁡(x)=x2−9⁢x+18x2−x−6

In Exercises 19-24, identify the horizontal and vertical asymptotes, if any, of the given function.

19. f⁡(x)=2⁢x2−2⁢x−4x2+x−20

20. f⁡(x)=−3⁢x2−9⁢x−65⁢x2−10⁢x−15

21. f⁡(x)=x2+2−127⁢x3−14⁢x2−21⁢x

22. f⁡(x)=x2−99⁢x−9

23. f⁡(x)=x2−99⁢x+27

24. f⁡(x)=x2−1−x2−1

In Exercises 25-28, evaluate the given limit.

25. limx→∞⁡x3+2⁢x2+1x−5

26. limx→∞⁡x3+2⁢x2+15−x

27. limx→∞⁡x3+2⁢x2+1x2−5

28. limx→∞⁡x3+2⁢x2+15−x2

Review

29. Use an ε−δ proof to show that limx→1⁡5⁢x−2=3.

30. Let limx→2⁡f⁡(x)=3 and limx→2⁡g⁡(x)=−1. Evaluate the following limits.
(a) limx→2⁡(f+g)⁡(x)
(b) limx→2⁡(f⁡g)⁢(x)
(c) limx→2⁡(f⁡/g)⁢(x)
(d) limx→2⁡f⁡(x)g⁡(x)

31. Let f⁡(x)={x2−1x<3x+5x≥3. Is f continuous everywhere?

32. Evaluate the limit: limx→c⁡ln⁡x.

1.E: Applications of Limits (Exercises) is shared under a CC BY-NC 3.0 license and was authored, remixed, and/or curated by LibreTexts.

  1. Back to top
  • Was this article helpful?

Recommended articles

  1. 1.1: An Introduction to LimitsThe foundation of "the calculus'' is the limit. It is a tool to describe a particular behavior of a function. This chapter begins our study of the lim...
  2. 1.2: Epsilon-Delta Definition of a LimitThis section introduces the formal definition of a limit. Many refer to this as "the epsilon--delta,'' definition, referring to the letters ϵ and δ ...
  3. 1.3: Finding Limits AnalyticallyRecognizing that ϵ-δ proofs are cumbersome, this section gives a series of theorems which allow us to find limits much more quickly and intuitively....
  4. 1.4: One Sided LimitsThe previous section gave us tools (which we call theorems) that allow us to compute limits with greater ease. Chief among the results were the facts ...
  5. 1.5: ContinuityAs we have studied limits, we have gained the intuition that limits measure 'where a function is heading.' We have seen, though, that this is not nece...
  1. Article type
    Section or Page
    License
    CC BY-NC
    License Version
    3.0
    Show Page TOC
    no
  2. Tags
    This page has no tags.

Support Center

How can we help?