Home
Bookshelves
Calculus
Calculus 3e (Apex)
1: Limits
1.E: Applications of Limits (Exercises)

1.E: Applications of Limits (Exercises)

Last updated
Save as PDF

Page ID: 9966

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1.1: An Introduction to Limits

Terms and Concepts

In your own words, what does it mean to "find the limit of $f(x)$ as $x$ approaches 3"?
An expression of the form $\frac00$ is called _____.
T/F: The limit of $f(x)$ as $x$ approaches 5 is $f(5)$.
Describe three situations where $\lim\limits_{x\to c}f(x)$ does not exist.
In your own words, what is a difference quotient.

Problems

In Exercises 6-16, approximate the given limits both numerically and graphically.

6. $\lim\limits_{x\to 1}x^2+3x-5$

7. $\lim\limits_{x\to 0}x^3-3x^2+x-5$

8. $\lim\limits_{x\to 0}\frac{x+1}{x^2+3x}$

9. $\lim\limits_{x\to 3}\frac{x^2-2x-3}{x^2-4x+3}$

10. $\lim\limits_{x\to-1}\frac{x^2+8x+7}{x^2+6x+5}$

11. $\lim\limits_{x\to 2}\frac{x^2+7x+10}{x^2-4x+4}$

12. $\lim\limits_{x\to 2}$, where $ f(x) = \begin{cases}x+2 \quad x\le 2\\ 3x-5 \quad x>2 \end{cases}.$

13. $\lim\limits_{x\to 3}$, where $ f(x) = \begin{cases}x^2-x+1 \quad & x\le 3\\ 2x+1 &x>3 \end{cases}.$

14. $\lim\limits_{x\to 0}$, where $ f(x) = \begin{cases}\cos x \quad & x\le 0\\ x^2+3x+1 &x>0 \end{cases}.$

15. $\lim\limits_{x\to \pi/2}$, where $ f(x) = \begin{cases}\sin x \quad & x\le \pi/2\\ \cos x &x>\pi/2 \end{cases}.$

In Exercises 16-24, a function $f$ and a value $a$ are given. Approximate the limit of the difference quotient, $\lim\limits_{h\to 0}\frac{f(a+h)-f(a)}{h}$, using $h=\pm 0.1,\, \pm 0.01.$

16. $f(x)=-7x+2,\quad a=3$

17. $f(x)=9x+0.06,\quad a=-1$

18. $f(x)=x^2+3x-7,\quad a=1$

19. $f(x)=\frac{1}{x+1},\quad a=2$

20. $f(x)=-4x^2+5x-1,\quad a=-3$

21. $f(x)=\ln x,\quad a=5$

22. $f(x)=\sin x,\quad a=\pi$

23. $f(x)=\cos x,\quad a=\pi$

1.2: Epsilon-Delta Definition of a Limit

Terms and Concepts

1. What is wrong with the following "definition" of a limit?

"The limit of $f(x)$, as x approaches $a$, is $K''$ means that given any $\delta >0$ there exists $\epsilon >0$ such that whenever $|f(x)-K|<\epsilon$, we have $|x-a|<\delta$.

2. Which is given first in establishing a limit, the x-tolerance or the y-tolerance?

3. T/F: $\epsilon$ must always be positive.

4. T/F: $\delta$ must always be positive.

Problems

In Exercises 5-11, prove the given limit using an $\epsilon -\delta$ proof.

5. $\lim\limits_{x\to5}3-x+-2$

6. $\lim\limits_{x\to3}x^2-3=6$

7. $\lim\limits_{x\to4}x^2+x-5=15$

8. $\lim\limits_{x\to2}x^3-1=7$

9. $\lim\limits_{x\to2}5=5$

10. $\lim\limits_{x\to0}e^{2x}-1=0$

11. $\lim\limits_{x\to0}\sin x = 0$ (Hint: use the fact that $|\sin x |\le |x|,$ with equality only when $x=0$.)

1.3: Finding Limits Analytically

Terms and Concepts

1. Explain in your own words, without using $ε-δ$ formality, why $\lim\limits_{x\to c}b=b$.

2. Explain in your own words, without using $ε-δ$ formality, why $\lim\limits_{x\to c}x=c$.

3. What does the text mean when it says that certain functions’ “behavior is ‘nice’ in terms of limits”? What, in particular, is “nice”?

4. Sketch a graph that visually demonstrates the Squeeze Theorem.

5. You are given the following information:

(a) $\lim\limits_{x\to1}f(x)=0$

(b)$\lim\limits_{x\to1}g(x)=0$

(c)$\lim\limits_{x\to1}f(x)/g(x) =2$

What can be said about the relative sizes of $f(x)$ and $g(x)$ as x approaches 1?

Problems

Using:

\[\begin{align}\lim\limits_{x\to9}f(x)=6 \qquad \lim\limits_{x\to6}f(x)=9 \\ \lim\limits_{x\to9}g(x)=3 \qquad \lim\limits_{x\to6}g(x)=3 \end{align}\]

evaluate the limits given in Exercises 6-13, where possible. If it is not possible to know, state so.

6. $\lim\limits_{x\to9}(f(x)+g(x))$

7. $\lim\limits_{x\to9}(3f(x)/g(x))$

8. $\lim\limits_{x\to9} \left ( \frac{f(x)-2g(x)}{g(x)}\right )$

9. $\lim\limits_{x\to6}\left (\frac{f(x)}{3-g(x)}\right )$

10. $\lim\limits_{x\to9}g(f(x))$

11. $\lim\limits_{x\to6}f(g(x))$

12. $\lim\limits_{x\to6}g(f(f(x)))$

13. $\lim\limits_{x\to6}f(x)g(x)-f^2(x)+g^2(x)$

Using

\[\begin{align}\lim\limits_{x\to1}f(x)=2 \qquad \lim\limits_{x\to10}f(x)=1 \\ \lim\limits_{x\to1}g(x)=0 \qquad \lim\limits_{x\to10}g(x)=\pi \end{align}\]

evaluate the limits given in Exercises 14-17, where possible. If it is not possible to know, state so.

14. $\lim\limits_{x\to1}f(x)^{g(x)}$

15. $\lim\limits_{x\to10}\cos (g(x))$

16. $\lim\limits_{x\to1}f(x)g(x)$

17. $\lim\limits_{x\to1}g(5f(x))$

In Exercises 18-32, evaluate the given limit.

18. $\lim\limits_{x\to3}x^2-3x+7$

19. $\lim\limits_{x\to\pi}\left ( \frac{x-3}{x+5}\right )^7$

20. $\lim\limits_{x\to\pi /4}\cos x \sin x$

21. $\lim\limits_{x\to 0}\ln x$

22. $\lim\limits_{x\to3}4^{{x^3}-8x}$

23. $\lim\limits_{x\to\pi/6}\csc x$

24. $\lim\limits_{x\to0}\ln (1+x)$

25. $\lim\limits_{x\to\pi}\frac{x^2+3x+5}{5x^2-2x-3}$

26.$\lim\limits_{x\to\pi}\frac{3x+1}{1-x}$

27.$\lim\limits_{x\to6}\frac{x^2-4x-12}{x^2-13x+42}$

28.$\lim\limits_{x\to0}\frac{x^2+2x}{x^2-2x}$

29.$\lim\limits_{x\to2}\frac{x^2+6x-16}{x^2-3x+2}$

30.$\lim\limits_{x\to2}\frac{x^2-5x-14}{x^2+10x+16}$

31.$\lim\limits_{x\to-2}\frac{x^2-5x-14}{x^2+10x+16}$

32.$\lim\limits_{x\to-1}\frac{x^2+9x+8}{x^2-6x-7}$\

Use the Squeeze Theorem in Exercises 33-36, where appropriate, to evaluate the given limit.

33. $\lim\limits_{x\to0} x\sin \left (\frac{1}{x}\right )$

34. $\lim\limits_{x\to0}\sin x \cos \left ( \frac{1}{x^2}\right )$

35. $\lim\limits_{x\to1}f(x)$, where $3x-2\le f(x)\le x^3.$

36. $\lim\limits_{x\to3+}f(x),$ where $6x-9\le f(x)\le x^2$ on [0,3].

Exercises 37-40, challenge your understanding of limits but can be evaluated using the knowledge gained in this section.

37. $\lim\limits_{x\to0}\frac{\sin 3x}{x}$

38. $\lim\limits_{x\to0}\frac{\sin 5x}{8x}$

39. $\lim\limits_{x\to0}\frac{\ln (1+x)}{x}$

40. $\lim\limits_{x\to0}\frac{\sin x}{x}$, where x is measured in degrees not radians.

1.4: One Sided Limits

Terms and Concepts

1. What are the three ways in which a limit may fail to exist?

2. T/F: If $\lim\limits_{x\to1-}f(x)=5$, then $\lim\limits_{x\to1}f(x)=5$

3. T/F: If $\lim\limits_{x\to1-}f(x)=5$, then $\lim\limits_{x\to1+}f(x)=5$

4. T/F: If $\lim\limits_{x\to1}f(x)=5$, then $\lim\limits_{x\to1-}f(x)=5$

Problems

In Exercises 5-12, evaluate each expression using the given graph of $f(x)$.

5.
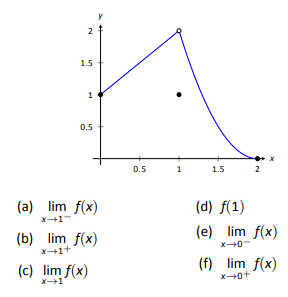
$clipboard_e4f5a8bce92d31a43cde475d21c7bbb8f.png$

6.
$146.PNG$

7.
$147.PNG$

8.
$148.PNG$

9.
$149.PNG$

10.
$1410.PNG$

11.
$1411.PNG$

12.
$1412.PNG$

In Exercises 13-21, evaluate the given limits of the piecewise defined functions $f$.

13. $f(x) = \begin{cases} x+1 \quad &x\le 1\\ x^2-5 &x>1 \end{cases}$
(a) $\lim\limits_{x\to1^-}f(x) $
(b) $\lim\limits_{x\to0^+}f(x)$
(c) $\lim\limits_{x\to1}f(x) $
(d) $f(1)$

14. $f(x) = \begin{cases} 2x^2+5x-1 \quad &x<0 \\ \sin x &x\ge 0 \end{cases}$
(a) $\lim\limits_{x\to0^-}f(x)$
(b) $\lim\limits_{x\to0^+}f(x)$
(c) $\lim\limits_{x\to0}f(x) $
(d) $f(0)$

15. $f(x) = \begin{cases} x^-1 \quad &x<-1 \\ x^3+1 &-1\le x \le 1 \\ x^2+1 &x>1 \end{cases}$
(a) $\lim\limits_{x\to-1^-}f(x)$
(b) $\lim\limits_{x\to1^+}f(x)$
(c) $\lim\limits_{x\to-1}f(x) $
(d) $f(-1)$
(e) $\lim\limits_{x\to1^-}f(x)$
(f) $\lim\limits_{x\to1^+}f(x)$
(g) $\lim\limits_{x\to1}f(x)$
(h) $f(1)$

16. $f(x) = \begin{cases} \cos x \quad &x<\pi \\ \sin x &x\ge \pi \end{cases}$
(a) $\lim\limits_{x\to\pi^-}f(x)$
(b) $\lim\limits_{x\to\pi^+}f(x)$
(c) $\lim\limits_{x\to\pi}f(x) $
(d) $f(\pi)$

17. $f(x) = \begin{cases} 1-\cos ^2 x \quad &x<a \\ \sin^2 x &x\ge a \end{cases}$, where $a$ is a real number.
(a) $\lim\limits_{x\to a^-}f(x)$
(b) $\lim\limits_{x\to a^+}f(x)$
(c) $\lim\limits_{x\to a}f(x) $
(d) $f(a)$

18. $f(x) = \begin{cases} x+1 \quad &x<1 \\ 1 &x=1 \\ x-1 &x>1 \end{cases}$
(a) $\lim\limits_{x\to1^-}f(x)$
(b) $\lim\limits_{x\to1^+}f(x)$
(c) $\lim\limits_{x\to1}f(x) $
(d) $f(1)$

19. $f(x) = \begin{cases} x^2 \quad &x<2 \\ x+1 &x=2 \\ -x^2+2x+4 &x>2 \end{cases}$
(a) $\lim\limits_{x\to2^-}f(x)$
(b) $\lim\limits_{x\to2^+}f(x)$
(c) $\lim\limits_{x\to2}f(x) $
(d) $f(2)$

20. $f(x) = \begin{cases} a(x-b)^2+c\quad &x<b \\ a(x-b)+c &x\ge b \end{cases}$, where a, b and c are real numbers.
(a) $\lim\limits_{x\to b^-}f(x)$
(b) $\lim\limits_{x\to b^+}f(x)$
(c) $\lim\limits_{x\to b}f(x) $
(d) $f(b)$

21. $f(x) = \begin{cases}\frac{|x|}{x} \quad &x\ne 0 \\ 0 &x= 0 \end{cases}$
(a) $\lim\limits_{x\to0^-}f(x)$
(b) $\lim\limits_{x\to0^+}f(x)$
(c) $\lim\limits_{x\to0}f(x) $
(d) $f(0)$

Review

22. Evaluate the limit: $\lim\limits_{x\to -1}\frac{x^2+5x+4}{x^2-3x-4}$

23. Evaluate the limit: $\lim\limits_{x\to -4}\frac{x^2-16}{x^2-4x-32}$

24. Evaluate the limit: $\lim\limits_{x\to -6}\frac{x^2-15x+54}{x^2-6x}$

25. Approximate the limit numerically: $\lim\limits_{x\to 0.4}\frac{x^2-4.4x+1.6}{x^2-0.4x}$

26. Approximate the limit numerically: $\lim\limits_{x\to 0.2}\frac{x^2+5.8x-1.2}{x^2-4.2x+0.8}$

1.5: Continuity

Terms and Concepts

1. In your own words, describe what it means for a function to be continuous.

2. In your own words, describe what the Intermediate Value Theorem states.

3. What is a “root” of a function?

4. Given functions $f\text{ and }g$ on an interval $I$, how can the Bisection Method be used to find a value c where $f(c) = g(c)$?

5. T/F: If $f$ is defined on an open interval containing c, and $\lim\limits_{x\to c} f(x)$ exists, then $f$ is continuous at c.

6. T/F: If $f$ is continuous at c, then $\lim\limits_{x\to c} f(x)$ exists

7. T/F: If $f$ is continuous at c, then $\lim\limits_{x\to c^+} f(x)=f(c)$.

8. T/F: If $f$ is continuous on [a, b], then $\lim\limits_{x\to a^-} f(x)=f(a)$.

9. T/F: If f is continuous on [0, 1) and [1, 2), then $f$ is continuous on [0, 2).

10. T/F: The sum of continuous functions is also continuous.

Problems

In Exercises 11-17, a graph of a function $f$ is given along with a value $a$. Determine if $f$ is continuous at $a$; if it is not, state why it is not.

11. $a=1$
$1511.PNG$

12. $a=1$
$1512.PNG$

13. $a=1$
$1513.PNG$

14. $a=0$
$1514.PNG$

15. $a=1$
$1515.PNG$

16. $a=4$
$1516.PNG$

17.
(a) $a=-2$
(b) $a=0$
(c) $a=2$
$1517.PNG$

In Exercises 18-21, determine if $f$ is continuous at the indicated values. If not, explain why.

18. $f(x) = \begin{cases} 1 \quad &x=0\\ \frac{\sin x}{x} &x>0 \end{cases}$
(a) $x=0$
(b) $x=\pi$

19. $f(x) = \begin{cases} x^3-x \quad &x<1\\ x-2 &x\ge 1 \end{cases}$
(a) $x=0$
(b) $x=1$

20. $f(x) = \begin{cases} \frac{x^2+5x+4}{x^2 +3x+2} \quad &x\ne -1\\ 3 &x=-1 \end{cases}$
(a) $x=-1$
(b) $x=10$

21. $f(x) = \begin{cases} \frac{x^2-64}{x^2-11x+24} \quad &x\ne 8\\ 5 &x=8 \end{cases}$
(a) $x=0$
(b) $x=8$

In Exercises 22-32, give the intervals on which the given function is continuous.

22. $f(x)=x^2-3x+9$

23. $g(x) = \sqrt{x^2-4}$

24. $h(k) = \sqrt{1-k}+\sqrt{k+1}$

25. $f(t) = \sqrt{5t^2-30}$

26. $g(t) = \frac{1}{\sqrt{1-t^2}}$

27. $g(x) = \frac{1}{1+x^2}$

28. $f(x) = e^x$

29. $g(s) = \ln s $

30. $h(t) = \cos t$

31. $f(k) = \sqrt{1-e^k}$

32. $f(x) = \sin (e^x+x^2)$

33. Let $f$ be continuous on [1,5] where $f(1) = -2 \text{ and }f(5)=-10$. Does a value $1<c<5$ exist such that $f(c)=-9$? Why/why not?

34. Let $g$ be continuous on [-3,7] where $g(0)=0 \text{ and }g(2)=25$. Does a value $-3<c<7$ exist such that $g(c)=15?$ Why/why not?

35. Let $f$ be continuous on [-1,1] where $f(-1)=-10 \text{ and }f(1)=10$. Does a value $-1<c<1$ exist such that $f(c)=11?$ Why/why not?

36. Let $h$ be continuous on [-1,1] where $h(-1)=-10 \text{ and }h(1)=10$. Does a value $-1<c<1$ exist such that $h(c)=0?$ Why/why not?

In Exercises 37-40, use the Bisection Method to approximate, accurate to two decimal places, the value of the root of the given function in the given interval.

37. $f(x) = x^2+2x-4\text{ on }[1,1.5]$.

38. $f(x) = \sin x -1/2\text{ on }[0.5,0.55]$.

39. $f(x) = e^x-2\text{ on }[0.65,0.7]$.

40. $f(x) = \cos x -\sin x \text{ on }[0.7,0.8]$.

Review

41. Let $f(x) = \begin{cases} x^2-5 \quad &x<5\\ 5x &x\ge 5 \end{cases}$.
(a) $\lim\limits_{x\to 5^-}f(x)$
(b) $\lim\limits_{x\to 5^+}f(x)$
(c) $\lim\limits_{x\to 5}f(x)$
(d) $f(5)$

42. Numerically approximate the following limits:
(a) $\lim\limits_{x\to 4/5^+}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$
(b) $\lim\limits_{x\to 4/5^-}\frac{x^2-8.2x-7.2}{x^2+5.8x+4}$

43. Give an example of function $f(x)$ for which $\lim\limits_{x\to 0}f(x)$ does not exist.

1.6: Limits Involving Infinity

Terms and Concepts

1. T/F: If $\lim\limits_{x\to 5}f(x)=\infty$, then we are implicitly stating that the limit exists.

2. T/F: If $\lim\limits_{x\to \infty}f(x)=5$, then we are implicitly stating that the limit exists.

3. T/F: If $\lim\limits_{x\to 1^-}f(x)=-\infty$, then $\lim\limits_{x\to 1^+}f(x)=\infty$.

4. T/F: If $\lim\limits_{x\to 5}f(x)=\infty$, then $f$ has a vertical asymptote at $x=5$.

5. T/F: $\infty/0$ is not an indeterminate form.

6. List 5 indeterminate forms.

7. Construct a function with a vertical asymptote at x = 5 and a horizontal asymptote at y = 5.

8. Let $\lim\limits_{x\to 7}f(x)=\infty$. Explain how we know that $f$ is/is not continuous at $x=7$.

Problems

In Exercises 9-14, evaluate the given limits using the graph of the function.

9. $f(x) = \frac{1}{(x+1)^2}$
(a) $\lim\limits_{x\to -1^-}f(x)$
(b) $\lim\limits_{x\to -1^+}f(x)$
$169.PNG$

10. $f(x) = \frac{1}{(x-3)(x-5)^2}$
(a) $\lim\limits_{x\to 3^-}f(x)$
(b) $\lim\limits_{x\to 3^+}f(x)$
(c) $\lim\limits_{x\to 3}f(x)$
(d) $\lim\limits_{x\to 5^-}f(x)$
(e) $\lim\limits_{x\to 5^+}f(x)$
(f) $\lim\limits_{x\to 5}f(x)$
$1610.PNG$

11. $f(x) = \frac{1}{e^x+1}$
(a) $\lim\limits_{x\to -\infty}f(x)$
(b) $\lim\limits_{x\to \infty}f(x)$
(c) $\lim\limits_{x\to 0^-}f(x)$
(d) $\lim\limits_{x\to 0^+}f(x)$
$1611.PNG$

12. $f(x) = x^2\sin (\pi x)$
(a) $\lim\limits_{x\to -\infty}f(x)$
(b) $\lim\limits_{x\to \infty}f(x)$
$1612.PNG$

13. $f(x)=\cos (x)$
(a) $\lim\limits_{x\to -\infty}f(x)$
(b) $\lim\limits_{x\to \infty}f(x)$
$1613.PNG$

14. $f(x) = 2^x +10$
(a) $\lim\limits_{x\to -\infty}f(x)$
(b) $\lim\limits_{x\to \infty}f(x)$
$1614.PNG$

In Exercises 15-18, numerically approximate the following limits:
(a) $\lim\limits_{x\to 3^-}f(x)$
(b) $\lim\limits_{x\to 3^+}f(x)$
(c) $\lim\limits_{x\to 3}f(x)$

15. $f(x) = \frac{x^2-1}{x^2-x-6}$

16. $f(x) = \frac{x^2+5x-36}{x^3-5x^2+3x+9}$

17. $f(x) = \frac{x^2-11x+30}{x^3-4x^2-3x+18}$

18. $f(x) = \frac{x^2-9x+18}{x^2-x-6}$

In Exercises 19-24, identify the horizontal and vertical asymptotes, if any, of the given function.

19. $f(x) = \frac{2x^2-2x-4}{x^2+x-20}$

20. $f(x) = \frac{-3x^2-9x-6}{5x^2-10x-15}$

21. $f(x) = \frac{x^2+2-12}{7x^3-14x^2-21x}$

22. $f(x) = \frac{x^2-9}{9x-9}$

23. $f(x) = \frac{x^2-9}{9x+27}$

24. $f(x) = \frac{x^2-1}{-x^2-1}$

In Exercises 25-28, evaluate the given limit.

25. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x-5}$

26. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x}$

27. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{x^2-5}$

28. $\lim\limits_{x\to \infty}\frac{x^3+2x^2+1}{5-x^2}$

Review

29. Use an $ε − δ$ proof to show that $\lim\limits_{x\to 1}5x-2=3$.

30. Let $\lim\limits_{x\to 2}f(x)=3\text{ and }\lim\limits_{x\to 2}g(x)=-1$. Evaluate the following limits.
(a) $\lim\limits_{x\to 2}(f+g)(x)$
(b) $\lim\limits_{x\to 2}(fg)(x)$
(c) $\lim\limits_{x\to 2}(f/g)(x)$
(d) $\lim\limits_{x\to 2}f(x)^{g(x)}$

31. Let $f(x) = \begin{cases}x^2-1 \qquad &x<3 \\ x+5 &x \ge 3 \end{cases}$. Is $f$ continuous everywhere?

32. Evaluate the limit: $\lim\limits_{x\to c}\ln x$.

Search

Text Color

Text Size

Margin Size

Font Type