6.7E: Exercises for Section 6.7
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 3, find the derivative dydx.
1) y=ln(2x)
- Answer
- dydx=1x
2) y=ln(2x+1)
3) y=1lnx
- Answer
- dydx=−1x(lnx)2
In exercises 4 - 5, find the indefinite integral.
4) ∫dt3t
5) ∫dx1+x
- Answer
- ∫dx1+x=ln|x+1|+C
In exercises 6 - 15, find the derivative dydx. (You can use a calculator to plot the function and the derivative to confirm that it is correct.)
6) [T] y=lnxx
7) [T] y=xlnx
- Answer
- dydx=ln(x)+1
8) [T] y=log10x
9) [T] y=ln(sinx)
- Answer
- dydx=cotx
10) [T] y=ln(lnx)
11) [T] y=7ln(4x)
- Answer
- dydx=7x
12) [T] y=ln((4x)7)
13) [T] y=ln(tanx)
- Answer
- dydx=cscxsecx
14) [T] y=ln(tan3x)
15) [T] y=ln(cos2x)
- Answer
- dydx=−2tanx
In exercises 16 - 25, find the definite or indefinite integral.
16) ∫10dx3+x
17) ∫10dt3+2t
- Answer
- ∫10dt3+2t=12ln(53)
18) ∫20xx2+1dx
19) ∫20x3x2+1dx
- Answer
- ∫20x3x2+1dx=2−12ln(5)
20) ∫e2dxxlnx
21) ∫e2dx(xlnx)2
- Answer
- ∫e2dx(xlnx)2=1ln(2)−1
22) ∫cosxsinxdx
23) ∫π/40tanxdx
- Answer
- ∫π/40tanxdx=12ln(2)
24) ∫cot(3x)dx
25) ∫(lnx)2xdx
- Answer
- ∫(lnx)2xdx=13(lnx)3
In exercises 26 - 35, compute dydx by differentiating lny.
26) y=√x2+1
27) y=√x2+1√x2−1
- Answer
- dydx=2x3√x2+1√x2−1
28) y=esinx
29) y=x−1/x
- Answer
- dydx=x−2−(1/x)(lnx−1)
30) y=eex
31) y=xe
- Answer
- dydx=exe−1
32) y=x(ex)
33) y=√x3√x6√x
- Answer
- dydx=1
34) y=x−1/lnx
35) y=e−lnx
- Answer
- dydx=−1x2
In exercises 36 - 40, evaluate by any method.
36) ∫105dtt−∫10x5xdtt
37) ∫eπ1dxx+∫−1−2dxx
- Answer
- π−ln(2)
38) ddx[∫1xdtt]
39) ddx[∫x2xdtt]
- Answer
- 1x
40) ddx[ln(secx+tanx)]
In exercises 41 - 44, use the function lnx. If you are unable to find intersection points analytically, use a calculator.
41) Find the area of the region enclosed by x=1 and y=5 above y=lnx.
- Answer
- (e5−6) units2
42) [T] Find the arc length of lnx from x=1 to x=2.
43) Find the area between lnx and the x-axis from x=1 to x=2.
- Answer
- ln(4)−1) units2
44) Find the volume of the shape created when rotating this curve from x=1 to x=2 around the x-axis, as pictured here.
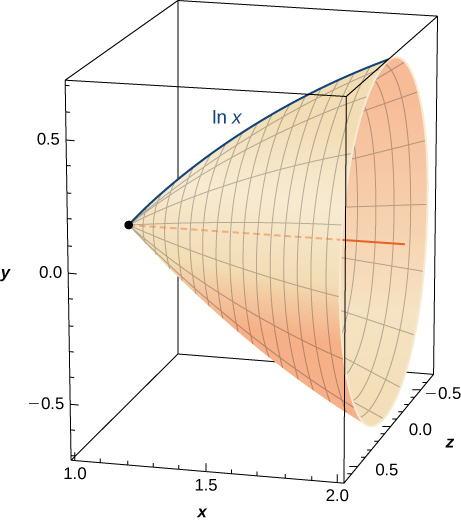
45) [T] Find the surface area of the shape created when rotating the curve in the previous exercise from x=1 to x=2 around the x-axis.
- Answer
- 2.8656 units2
If you are unable to find intersection points analytically in the following exercises, use a calculator.
46) Find the area of the hyperbolic quarter-circle enclosed by x=2 and y=2 above y=1/x.
47) [T] Find the arc length of y=1/x from x=1 to x=4.
- Answer
- s=3.1502 units
48) Find the area under y=1/x and above the x-axis from x=1 to x=4.
In exercises 49 - 53, verify the derivatives and antiderivatives.
49) ddx[ln(x+√x2+1)]=1√1+x2
50) ddx[ln(x−ax+a)]=2a(x2−a2)
51) ddx[ln(1+√1−x2x)]=−1x√1−x2
52) ddx[ln(x+√x2−a2)]=1√x2−a2
53) ∫dxxln(x)ln(lnx)=ln|ln(lnx)|+C
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


