2.6: Some Techniques for Evaluating Integrals

2.6.1 Change of Variable

If \(F\) is an integral of \(f\) and \(\varphi\) is a differentiable function, then, using the chain rule,

\[\frac{d}{d x} F(\varphi(x))=F^{\prime}(\varphi(x)) \varphi^{\prime}(x)=f(\varphi(x)) \varphi^{\prime}(x).\]

Written in terms of integrals, we have

\[\int f(\varphi(x)) \varphi^{\prime}(x) d x=F(\varphi(x))+c.\]

If we let \(u=\varphi(x)\) and note that

\[\int f(u) d u=F(u)+c,\]

we may express \((2.6.2)\) as

\[\int f(\varphi(x)) \varphi^{\prime}(x) d x=\int f(u) d u.\]

That is, we may evaluate

\[\int f(\varphi(x)) \varphi^{\prime}(x) d x,\]

by changing the variable to \(u=\varphi(x),\) with \(\varphi^{\prime}(x) d x\) becoming \(d u\) since

\[\frac{d u}{d x}=\varphi^{\prime}(x).\]

Example \(\PageIndex{1}\)

To evaluate

\[\int 2 x \sqrt{1+x^{2}} d x,\]

let

\[\begin{aligned} u &=1+x^{2} \\ d u &=2 x d x. \end{aligned}\]

Then

\[\int 2 x \sqrt{1+x^{2}} d x=\int \sqrt{u} d u=\frac{2}{3} u^{\frac{3}{2}}+c=\frac{2}{3}\left(1+x^{2}\right)^{\frac{3}{2}}+c.\]

Example \(\PageIndex{2}\)

To evaluate

\[\int x \sin \left(x^{2}\right) d x,\]

let

\[\begin{aligned} u &=x^{2} \\ d u &=2 x d x \end{aligned}\]

Note that in this case we cannot make a direct substitution of \(u\) and \(d u\) since \(d u=2 x d x\) does not appear as part of the integral. However, \(d u\) differs from \(x d x\) by only a constant factor, and we may rewrite \(d u=2 x d x\) as

\[\frac{1}{2} d u=x d x.\]

Now we may perform the change of variable:

\[\int x \sin (u) d x=\frac{1}{2} \int \sin (u) d u=-\frac{1}{2} \cos (u)+c=-\frac{1}{2} \cos \left(x^{2}\right)+c.\]

Example \(\PageIndex{3}\)

Note that we could evaluate the integral

\[\int \cos (4 x) d x\]

using the substitution

\[\begin{aligned} u &=4 x \\ d u &=4 d x, \end{aligned}\]

which gives us

\[\int \cos (4 x) d x=\frac{1}{4} \int \cos (u) d u=\frac{1}{4} \sin (u)+c=\frac{1}{4} \sin (4 x)+c.\]

However, it is probably quicker, and easier, to guess that the integral of \(\cos (4 x)\) should be close to \(\sin (4 x),\) and then correcting this guess appropriately after noting that

\[\frac{d}{d x} \sin (4 x)=4 \cos (4 x).\]

Example \(\PageIndex{4}\)

To evaluate

\[\int \cos ^{2}(5 x) \sin (5 x) d x,\]

let

\[\begin{aligned} u &=\cos (5 x) \\ d u &=-5 \sin (5 x) d x \end{aligned}.\]

Then

\[\int \cos ^{2}(5 x) \sin (5 x) d x=-\frac{1}{5} \int u^{2} d u=-\frac{1}{15} u^{3}+c=-\frac{1}{15} \cos ^{3}(5 x)+c.\]

Now consider the definite integral

\[\int_{a}^{b} f(\varphi(x)) \varphi^{\prime}(x) d x.\]

If \(F\) is an integral of \(f, c=\varphi(a),\) and \(d=\varphi(b),\) then \[\begin{aligned} \int_{a}^{b} f(\varphi(x)) \varphi^{\prime}(x) d x &=F(\varphi(x)))_{a}^{b} \\ &=F(\varphi(b))-F(\varphi(a)) \\ &=F(d)-F(c) \\ &=\left.F(u)\right|_{c} ^{d} \\ &=\int_{c}^{d} f(u) d u .\end{aligned}\] That is, we may use a change of variable to evaluate a definite integral in the same manner as above, the only difference being that we must change the limits of integration to reflect the values of the new variable \(u .\)

Example \(\PageIndex{5}\)

To evaluate

\[\int_{0}^{1} \frac{x}{\sqrt{1+x^{2}}} d x,\] let \[\begin{aligned} u &=1+x^{2} \\ d u &=2 x d x. \end{aligned}\] Note that when \(x=0, u=1,\) and when \(x=1, u=2 .\) Hence \[\int_{0}^{1} \frac{x}{\sqrt{1+x^{2}}} d x=\frac{1}{2} \int_{1}^{2} \frac{1}{\sqrt{u}} d u=\left.\sqrt{u}\right|_{1} ^{2}=\sqrt{2}-1.\]

Example \(\PageIndex{6}\)

To evaluate

\[\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x,\] let \[\begin{aligned} u &=\cos (2 x) \\ d u &=-2 \sin (2 x) d x. \end{aligned}\] \[\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x=-\frac{1}{2} \int_{1}^{0} u^{2} d u.\] Note that, after making the change of variable, the upper limit of integration is less than the lower limit of integration, a situation not covered by our definition of the definite integral or our statement of the fundamental theorem of calculus. However, the result on substitutions above shows that we will obtain the correct result if we apply the fundamental theorem as usual. Moreover, this points toward an extension of our definition: if \(b<a,\) then we should have \[\int_{a}^{b} f(x) d x=-\int_{b}^{a} f(x) d x,\] which is consistent with both the fundamental theorem of calculus and with the definition of the definite integral (since, if \(b<a, d x=\frac{b-a}{N}<0\) for any positive infinite integer \(N) .\) With this, we may finish the evaluation: \[\int_{0}^{\frac{\pi}{4}} \cos ^{2}(2 x) \sin (2 x) d x=-\frac{1}{2} \int_{1}^{0} u^{2} d u=\frac{1}{2} \int_{0}^{1} u^{2} d u=\left.\frac{u^{3}}{6}\right|_{0} ^{1}=\frac{1}{6}.\]

Exercise \(\PageIndex{1}\)

Evaluate \(\int 3 x^{2} \sqrt{1+x^{3}} d x\).

Answer

\(\int 3 x^{2} \sqrt{1+x^{3}} d x=\frac{2}{3}\left(1+x^{3}\right)^{\frac{3}{2}}+c\)

Exercise \(\PageIndex{2}\)

Evaluate \(\int x \sqrt{4+3 x^{2}} d x\).

Answer

\(\int x \sqrt{4+3 x^{2}} d x=\frac{1}{9}\left(4+3 x^{2}\right)^{\frac{3}{2}}+c\)

Exercise \(\PageIndex{3}\)

Evaluate \(\int \sec ^{2}(3 x) \tan ^{2}(3 x) d x\).

Answer

\(\int \sec ^{2}(4 x) \tan ^{2}(4 x) d x=\frac{1}{12} \tan ^{3}(4 x)+c\)

Exercise \(\PageIndex{4}\)

Evaluate \(\int_{0}^{2} \frac{x}{\sqrt{4+x^{2}}} d x\).

Answer

\(\int_{0}^{2} \frac{x}{\sqrt{4+x^{2}}} d x=2 \sqrt{2}-2\)

Exercise \(\PageIndex{5}\)

Evaluate \(\int_{0}^{\frac{\pi}{6}} \sin (3 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{2}} \sin (3 x) d x=\frac{2}{3}\)

Exercise \(\PageIndex{6}\)

Evaluate \(\int_{0}^{\frac{\pi}{2}} \sin ^{4}(2 x) \cos (2 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{4}} \sin ^{4}(2 x) \cos (2 x) d x=\frac{1}{10}\)

2.6.2 Integration by Parts

Suppose \(u\) and \(v\) are both differentiable functions of \(x .\) Since, by the product rule,

\[\frac{d}{d x} u v=u \frac{d v}{d x}+v \frac{d u}{d x},\] we have \[u \frac{d v}{d x}=\frac{d}{d x} u v-v \frac{d u}{d x}.\] Hence, integrating both sides with respect to \(x\), \[\int u \frac{d v}{d x} d x=\int \frac{d}{d x} u v-\int v \frac{d u}{d x}=u v-\int v \frac{d u}{d x} d x,\] which we may write as \[\int u d v=u v-\int v d u.\] This last formulation, known as integration by parts, is useful whenever the integral on the right of \((2.6 .10)\) is in someway simpler than the integral on the left. The next examples will illustrate some typical cases.

Example \(\PageIndex{7}\)

Consider the integral

\[\int x \cos (x) d x.\] If we let \(u=x\) and \(d v=\cos (x) d x,\) then \(d u=d x\) and we may let \(v=\sin (x)\). Note that we have some choice for \(v\) since the only requirement is that it is an integral of \(\cos (x) .\) Using \((2.6 .10),\) we have \[\int x \sin (x) d x=u v-\int v d u=x \sin (x)-\int \sin (x) d x=x \sin (x)+\cos (x)+c.\] In evaluating a definite integral using integration by parts, we must remember to evaluate each piece of the integral. That is, \[\int u d v=\left.u v\right|_{a} ^{b}-\int_{a}^{b} v d u.\]

Example \(\PageIndex{8}\)

To evaluate

\[\int_{0}^{\pi} x^{2} \sin (x) d x,\] let \[\begin{aligned} u &=x^{2} & & d v=\sin (x) d x \\ d u &=2 x d x & & v=-\cos (x). \end{aligned}\] Then, using \((2.6.11)\), \[\int_{0}^{\pi} x^{2} \sin (x) d x=-\left.x^{2} \cos (x)\right|_{0} ^{\pi}+\int_{0}^{\pi} 2 x \cos (x) d x=\pi^{2}+\int_{0}^{\pi} 2 x \cos (x) d x.\] \[\begin{aligned} u &=2 x & & d v=\cos (x) \\ d u &=2 d x & & v=\sin (x), \end{aligned}\] we have \[\begin{aligned} \int_{0}^{\pi} x^{2} \sin (x) d x &=\pi^{2}+\left.2 x \sin (x)\right|_{0} ^{\pi}-\int_{0}^{\pi} 2 \sin (x) d x \\ &=\pi^{2}+(0-0)+\left.2 \cos (x)\right|_{0} ^{\pi} \\ &=\pi^{2}-2-2 \\ &=\pi^{2}-4. \end{aligned}\]

Example \(\PageIndex{9}\)

To evaluate

\[\int_{0}^{1} x \sqrt{1+x} d x,\] let \[\begin{aligned} u &=x & & d v=\sqrt{1+x} d x \\ d u &=d x & & v=\frac{2}{3}(1+x)^{\frac{3}{2}} .\end{aligned}\] Then \[\begin{aligned} \int_{0}^{1} x \sqrt{1+x} d x &=\left.\frac{2}{3} x(1+x)^{\frac{3}{2}}\right|_{0} ^{1}-\frac{2}{3} \int_{0}^{1}(1+x)^{\frac{3}{2}} d x \\ &=\frac{4 \sqrt{2}}{3}-\left.\frac{4}{15}(1+x)^{\frac{5}{2}}\right|_{0} ^{1} \\ &=\frac{4 \sqrt{2}}{3}-\frac{16 \sqrt{2}-4}{15} \\ &=\frac{4 \sqrt{2}+4}{15}. \end{aligned}\]

Exercise \(\PageIndex{7}\)

Evaluate \(\int x \sin (2 x) d x\).

Answer

\(\int x \sin (2 x) d x=-\frac{1}{2} x \cos (2 x)+\frac{1}{4} \sin (2 x)+c\)

Exercise \(\PageIndex{8}\)

Evaluate \(\int x^{2} \cos (3 x) d x\).

Answer

\(\int x^{2} \cos (3 x) d x=\frac{1}{3} x^{2} \sin (3 x)+\frac{2}{9} x \cos (3 x)-\frac{2}{27} \sin (3 x)+c\)

Exercise \(\PageIndex{9}\)

Evaluate \(\int_{0}^{\pi} x \cos \left(\frac{1}{2} x\right) d x\).

Answer

\(\int_{0}^{\pi} x \cos \left(\frac{1}{2} x\right) d x=2 \pi-4\)

Exercise \(\PageIndex{10}\)

Evaluate \(\int_{0}^{\frac{\pi}{2}} 3 x^{2} \cos \left(x^{2}\right) d x\).

Answer

\(\int_{0}^{\frac{\pi}{2}} 3 x^{2} \cos \left(x^{2}\right) d x=-6 \pi\)

Exercise \(\PageIndex{11}\)

Evaluate \(\int_{0}^{2} x^{2} \sqrt{1+x} d x\).

Answer

\(\int_{0}^{2} x^{2} \sqrt{1+x} d x=\frac{264 \sqrt{3}-16}{105}\)

2.6.3 Some Integrals Involving Trigonometric Functions

The next examples will illustrate how various identities are useful in simplifying some integrals involving trigonometric functions.

Example \(\PageIndex{10}\)

To evaluate the integral

\[\int_{0}^{\pi} \sin ^{2}(x) d x,\] we will use the half-angle formula: \[\sin ^{2}(x)=\frac{1-\cos (2 x)}{2}.\] Then \[\begin{aligned} \int_{0}^{\pi} \sin ^{2}(x) d x &=\frac{1}{2} \int_{0}^{\pi}(1-\cos (2 x)) d x \\ &=\left.\frac{1}{2} x\right|_{0} ^{\pi}-\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\pi} \\ &=\frac{\pi}{2} .\end{aligned}\]

There is also a half-angle formula for cosine, namely,

\[\cos ^{2}(x)=\frac{1+\cos (2 x)}{2}.\]

As illustrated in the next example, we may use the half-angle formulas recursively to evaluate the integral of any even power of sine or cosine.

Example \(\PageIndex{11}\)

Using 2.6 .13 twice, we have

\[\begin{aligned} \int_{0}^{\pi} \cos ^{4}(3 x) d x &=\int_{0}^{\pi}\left(\cos ^{2}(3 x)\right)^{2} d x \\ &=\int_{0}^{\pi}\left(\frac{1}{2}(1+\cos (6 x))\right)^{2} d x \\ &=\frac{1}{4} \int_{0}^{\pi}\left(1+2 \cos (6 x)+\cos ^{2}(6 x)\right) d x \\ &=\left.\frac{1}{4} x\right|_{0} ^{\pi}+\left.\frac{1}{12} \sin (6 x)\right|_{0} ^{\pi}+\frac{1}{8} \int_{0}^{\pi}(1+\cos (12 x)) d x \\ &=\frac{\pi}{4}+\left.\frac{1}{8} x\right|_{0} ^{\pi}+\left.\frac{1}{96} \sin (12 x)\right|_{0} ^{\pi} \\ &=\frac{3 \pi}{8} . \end{aligned}\]

Exercise \(\PageIndex{12}\)

Evaluate \(\int_{0}^{\pi} \sin ^{2}(2 x) d x\).

Answer

\(\int_{0}^{\pi} \sin ^{2}(2 x) d x=\frac{\pi}{2}\)

Exercise \(\PageIndex{13}\)

Evaluate \(\int_{0}^{\pi} \cos ^{2}(3 x) d x\).

Answer

\(\int_{0}^{\pi} \cos ^{2}(3 x) d x=\frac{\pi}{2}\)

Exercise \(\PageIndex{14}\)

Evaluate \(\int \cos ^{4}(x) d x\).

Answer

\(\int \cos ^{4}(x) d x=\frac{3}{8} x+\frac{1}{4} \sin (2 x)+\frac{1}{32} \sin (4 x)+c\)

The next example illustrates a reduction formula.

Example \(\PageIndex{12}\)

Suppose \(n \geq 2\) is an integer and we wish to evaluate

\[\int_{0}^{\pi} \sin ^{n}(x) d x.\] We begin with an integration by parts: if we let \[\begin{aligned} u &=\sin ^{n-1}(x) & & d v=\sin (x) d x \\ d u &=(n-1) \sin ^{n-2}(x) \cos (x) d x & & v=-\cos (x), \end{aligned}\] then \[\begin{aligned} \int_{0}^{\pi} \sin ^{n}(x) d x &=-\left.\sin ^{n-1}(x) \cos (x)\right|_{0} ^{\pi}+(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) \cos ^{2}(x) d x \\ &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) \cos ^{2}(x) d x . \end{aligned}\] Now \(\cos ^{2}(x)=1-\sin ^{2}(x),\) so we have \[\begin{aligned} \int_{0}^{\pi} \sin ^{n}(x) d x &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x)\left(1-\sin ^{2}(x)\right) d x \\ &=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) d x-(n-1) \int_{0}^{\pi} \sin ^{n}(x) d x . \end{aligned}\] Notice that \(\int_{0}^{\pi} \sin ^{n}(x) d x\) occurs on both sides of this equation. Hence we may solve for this quantity, first obtaining \[n \int_{0}^{\pi} \sin ^{n}(x) d x=(n-1) \int_{0}^{\pi} \sin ^{n-2}(x) d x,\] and then \[\int_{0}^{\pi} \sin ^{n}(x) d x=\frac{n-1}{n} \int_{0}^{\pi} \sin ^{n-2}(x) d x.\] Note that, although we have not yet found the value of our integral, we have reduced the power of \(\sin (x)\) in the integral. We may now use \((2.6 .14)\) repeatedly to reduce the power of \(\sin (x)\) until we can easily evaluate the resulting integral. For example, if \(n=6\) we have \[\begin{aligned} \int_{0}^{\pi} \sin ^{6}(x) d x &=\frac{5}{6} \int_{0}^{\pi} \sin ^{4}(x) d x \\ &=\frac{5}{6} \frac{3}{4} \int_{0}^{\pi} \sin ^{2}(x) d x \\ &=\frac{5}{6} \frac{3}{4} \frac{1}{2} \int_{0}^{\pi} d x \\ &=\frac{5 \pi}{16} . \end{aligned}\] Similarly, \[\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=\frac{4}{5} \int_{0}^{\pi} \sin ^{3}(x) d x \\ &=\frac{4}{5} \frac{2}{3} \int_{0}^{\pi} \sin (x) d x \\ &=-\left.\frac{8}{15} \cos (x)\right|_{0} ^{\pi} \\ &=\frac{16}{15} . \end{aligned}\]

Exercise \(\PageIndex{15}\)

Use the reduction formula (2.6.14) to evaluate

\[\int_{0}^{\pi} \sin ^{8}(x) d x .\]

Answer

\(\int_{0}^{\pi} \sin ^{8}(x) d x=\frac{35 \pi}{128}\)

Exercise \(\PageIndex{16}\)

Use the reduction formula \((2.6.14)\) to evaluate

\[\int_{0}^{\pi} \sin ^{7}(x) d x .\]

Answer

\(\int_{0}^{\pi} \sin ^{7}(x) d x=\frac{32}{35}\)

Exercise \(\PageIndex{17}\)

Derive the reduction formula

\[\int_{0}^{\pi} \cos ^{n}(x)=\frac{n-1}{n} \int_{0}^{\pi} \cos ^{n-2}(x) d x ,\] where \(n \geq 2\) is an integer.

Exercise \(\PageIndex{18}\)

Use the reduction formula of the previous exercise to evaluate

\[\int_{0}^{\pi} \cos ^{6}(x) d x .\]

Answer

\(\int_{0}^{\pi} \cos ^{6}(x) d x=\frac{5 \pi}{16}\)

Exercise \(\PageIndex{19}\)

Derive the reduction formulas

\[\int \sin ^{n}(x) d x=-\frac{1}{n} \sin ^{n-1}(x) \cos (x)+\frac{n-1}{n} \int \sin ^{n-2}(x) d x \] and \[\int \cos ^{n}(x) d x=\frac{1}{n} \cos ^{n-1}(x) \sin (x)+\frac{n-1}{n} \int \cos ^{n-2}(x) d x ,\] where \(n \geq 2\) is an integer.

Example \(\PageIndex{13}\)

An alternative to using a reduction formula in the last example begins with noting that

\[\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=\int_{0}^{\pi} \sin ^{4}(x) \sin (x) d x \\ &=\int_{0}^{\pi}\left(\sin ^{2}(x)\right)^{2} \sin (x) d x \\ &=\int_{0}^{\pi}\left(1-\cos ^{2}(x)\right)^{2} \sin (x) d x \\ &=\int_{0}^{\pi}\left(1-2 \cos ^{2}(x)+\cos ^{4}(x)\right) \sin (x) d x . \end{aligned}\] The latter integral may now be evaluated using the change of variable \[\begin{aligned} u &=\cos (x) \\ d u &=-\sin (x) d x , \end{aligned}\] giving us \[\begin{aligned} \int_{0}^{\pi} \sin ^{5}(x) d x &=-\int_{1}^{-1}\left(1-2 u^{2}+u^{4}\right) d u \\ &=\int_{-1}^{1}\left(1-2 u^{2}+u^{4}\right) d u \\ &=\left.\left(u-\frac{2}{3} u^{3}+\frac{1}{5} u^{5}\right)\right|_{-1} ^{1} \\ &=\left(1-\frac{2}{3}+\frac{1}{5}\right)-\left(-1+\frac{2}{3}-\frac{1}{5}\right) \\ &=\frac{16}{15} , \end{aligned}\] as we saw above.

Exercise \(\PageIndex{20}\)

Evaluate \(\int_{0}^{\frac{\pi}{4}} \cos ^{5}(2 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{4}} \cos ^{5}(2 x) d x=\frac{4}{15}\)

\[\begin{array}{l}{\sin ((a+b) x)=\sin (a x) \cos (b x)+\sin (b x) \cos (a x)} \\ {\sin ((a-b) x)=\sin (a x) \cos (b x)-\sin (b x) \cos (b x)} . \end{array}\]

Adding these together, we have \[2 \sin (a x) \cos (b x)=\sin ((a+b) x)+\sin ((a-b) x) ,\] and so \[\sin (a x) \cos (b x)=\frac{1}{2}(\sin ((a+b) x)+\sin ((a-b) x)) .\]

Example \(\PageIndex{14}\)

To evaluate

\[\int_{0}^{\pi} \sin (2 x) \cos (3 x) d x ,\] we first note that, using \((2.6 .18)\) with \(a=2\) and \(b=3\), \[\sin (2 x) \cos (3 x)=\frac{1}{2}(\sin (5 x)+\sin (-x))=\frac{1}{2}(\sin (5 x)-\sin (x)) .\] Hence \[\begin{aligned} \int_{0}^{\pi} \sin (2 x) \cos (3 x) d x &=\frac{1}{2} \int_{0}^{\pi} \sin (5 x) d x-\frac{1}{2} \int_{0}^{\pi} \sin (x) d x \\ &=-\left.\frac{1}{10} \cos (5 x)\right|_{0} ^{\pi}+\left.\frac{1}{2} \cos (x)\right|_{0} ^{\pi} \\ &=\left(\frac{1}{10}+\frac{1}{10}\right)+\left(-\frac{1}{2}-\frac{1}{2}\right) \\ &=-\frac{4}{5} . \end{aligned}\] For integrals involving \(\sin (a x) \sin (b x),\) we begin with the the angle addition and subtraction formulas for cosine, \[\begin{array}{l}{\cos ((a+b) x)=\cos (a x) \cos (b x)-\sin (b x) \sin (a x)} \\ {\cos ((a-b) x)=\cos (a x) \cos (b x)+\sin (b x) \sin (b x)} . \end{array}\] Subtracting the first of these from the second, we have \[2 \sin (a x) \sin (b x)=\cos ((a-b) x)-\cos ((a+b) x) ,\] and so \[\sin (a x) \sin (b x)=\frac{1}{2}(\cos ((a-b) x)-\cos ((a+b) x)) .\]

Example \(\PageIndex{15}\)

To evaluate

\[\int_{0}^{\pi} \sin (3 x) \sin (5 x) d x ,\] we first note that, using \((2.6.22)\) with \(a=3\) and \(b=5\), \[\sin (3 x) \sin (5 x)=\frac{1}{2}(\cos (-2 x)-\cos (8 x))=\frac{1}{2}(\cos (2 x)-\cos (8 x)) .\] Note that we would have the same identity if we had chosen \(a=5\) and \(b=3 .\) Then \[\begin{aligned} \int_{0}^{\pi} \sin (3 x) \sin (5 x) d x &=\frac{1}{2} \int_{0}^{\pi} \cos (2 x) d x-\frac{1}{2} \int_{0}^{\pi} \cos (8 x) d x \\ &=\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\pi}-\left.\frac{1}{16} \sin (8 x)\right|_{0} ^{\pi} \\ &=0 . \end{aligned}\] For integrals involving \(\cos (a x) \cos (b x),\) we add \((2.6 .19)\) to \((2.6 .20)\) to obtain \[2 \cos (a x) \cos (b x)=\cos ((a+b) x)+\cos ((a-b) x) ,\] which leads to \[\cos (a x) \cos (b x)=\frac{1}{2}(\cos ((a+b) x)+\cos ((a-b) x)) .\]

Example \(\PageIndex{16}\)

To evaluate

\[\int_{0}^{\frac{\pi}{2}} \cos (3 x) \cos (5 x) d x ,\] we note that, using \((2.6 .24)\) with \(a=3\) and \(b=5\), \[\cos (3 x) \cos (5 x)=\frac{1}{2}(\cos (8 x)+\cos (-2 x))=\frac{1}{2}(\cos (8 x)+\cos (2 x)) .\] Hence \[\begin{aligned} \int_{0}^{\frac{\pi}{2}} \cos (3 x) \cos (5 x) d x &=\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \cos (8 x) d x+\frac{1}{2} \int_{0}^{\frac{\pi}{2}} \cos (2 x) d x \\ &=\left.\frac{1}{16} \sin (8 x)\right|_{0} ^{\frac{\pi}{2}}-\left.\frac{1}{4} \sin (2 x)\right|_{0} ^{\frac{\pi}{2}} \\ &=0 . \end{aligned}\]

Exercise \(\PageIndex{21}\)

Evaluate \(\int_{0}^{\frac{\pi}{2}} \sin (x) \cos (2 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{2}} \sin (2 x) \sin (x) d x=-\frac{1}{3}\)

Exercise \(\PageIndex{22}\)

Evaluate \(\int_{0}^{\frac{\pi}{2}} \sin (x) \sin (2 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{2}} \sin (x) \sin (2 x) d x=\frac{2}{3}\)

Exercise \(\PageIndex{23}\)

Evaluate

\[\int_{0}^{\frac{\pi}{2}} \sin (3 x) \cos (3 x) d x .\] Note: This may be evaluated with a substitution.

Answer

\(\int_{0}^{\frac{\pi}{2}} \sin (3 x) \cos (3 x) d x=\frac{1}{6}\)

Exercise \(\PageIndex{24}\)

Evaluate \(\int_{0}^{\frac{\pi}{2}} \cos (x) \cos (2 x) d x\).

Answer

\(\int_{0}^{\frac{\pi}{2}} \cos (x) \cos (2 x) d x=\frac{1}{3}\)

Exercise \(\PageIndex{25}\)

For any positive integers \(m\) and \(n,\) show that

\[\int_{0}^{2 \pi} \sin (m x) \cos (n x) d x=0 ,\] \[\int_{0}^{2 \pi} \sin (m x) \sin (n x) d x=\left\{\begin{array}{ll}{0,} & {\text { if } m \neq n,} \\ {\pi} & {\text { if } m=n,}\end{array}\right.\] and \[\int_{0}^{2 \pi} \cos (m x) \cos (n x) d x=\left\{\begin{array}{ll}{0,} & {\text { if } m \neq n,} \\ {\pi,} & {\text { if } m=n.}\end{array}\right.\]

2.6.4 Change of Variable Revisited

Suppose \(f\) is a continuous function on the interval \([a, b]\) and \(\varphi\) is either an increasing function defined on an interval \([c, d]\) with \(\varphi(c)=a\) and \(\varphi(d)=b,\) or a decreasing function defined on \([c, d]\) with \(\varphi(c)=b\) and \(\varphi(d)=a .\) Then, by \((2.6 .5),\) changing the notation as necessary,

\[\int_{a}^{b} f(x) d x=\int_{c}^{d} f(\varphi(z)) \varphi^{\prime}(z) d z .\] Earlier we used \((2.6 .25)\) to simplify integrals in the form of the right-hand side; in this section we will look at some examples which simplify in the other direction.

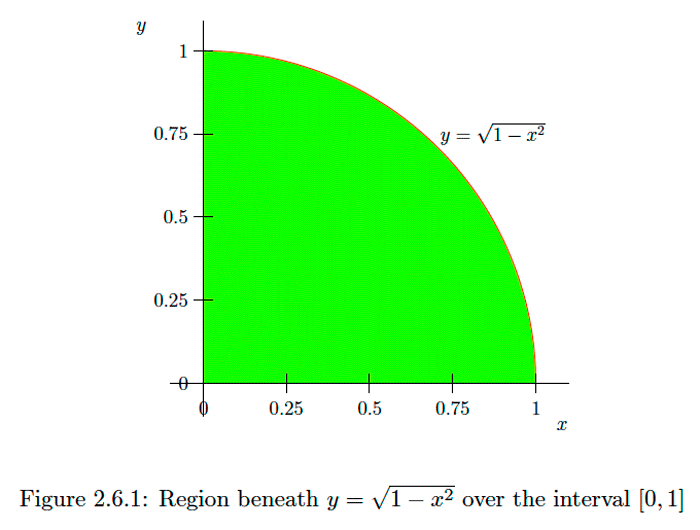
Example \(\PageIndex{17}\)

Since the graph of \(y=\sqrt{1-x^{2}}\) for \(0 \leq x \leq 1\) is one-quarter of the circle \(\left.x^{2}+y^{2}=1 \text { (see Figure } 2.6 .1\right),\) we know that

\[\int_{0}^{1} \sqrt{1-x^{2}} d x=\frac{\pi}{4} .\] We will now see how to use a change of variable to evaluate this integral using the fundamental theorem. The idea is to make use of the trigonometric identity \(1-\sin ^{2}(z)=\cos ^{2}(z) .\) That is, suppose we let \(x=\sin (z)\) for \(0 \leq z \leq \frac{\pi}{2} .\) Then \[\sqrt{1-x^{2}}=\sqrt{1-\sin ^{2}(z)}=\sqrt{\cos ^{2}(z)}=|\cos (z)|=\cos (z) ,\] where the final equality follows since \(\cos (z) \geq 0\) for \(0 \leq z \leq \frac{\pi}{2} .\) Now \[d x=\cos (z) d z ,\]

so we have

\[\begin{aligned} \int_{0}^{1} \sqrt{1-x^{2}} d x &=\int_{0}^{\frac{\pi}{2}} \cos (z) \cos (z) d z \\ &=\int_{0}^{\frac{\pi}{2}} \cos ^{2}(z) d z \\ &=\frac{1}{2} \int_{0}^{\frac{\pi}{2}}(1+\cos (2 z)) d z \\ &=\left.\frac{1}{2} z\right|_{0} ^{\frac{\pi}{2}}+\left.\frac{1}{4} \sin (2 z)\right|_{0} ^{\frac{\pi}{2}} \\ &=\frac{\pi}{4} , \end{aligned}\] as we expected.

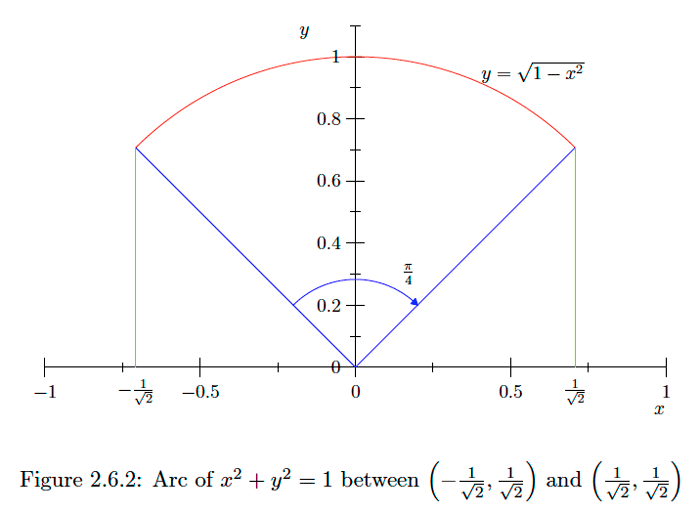
Example \(\PageIndex{18}\)

Let \(C\) be the circle with equation \(x^{2}+y^{2}=1\) and let \(L\) be the length of the shorter arc of \(C\) between \(\left(-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) and \(\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\) (see Figure \(2.6 .2) .\) since the circumference of \(C\) is \(2 \pi\) and this arc is one-fourth of the circumference of \(C,\) we should have \(L=\frac{\pi}{2} .\) We will now show that this agrees with \((2.5 .28),\) the formula we derived for computing arc length. Now \(y=\sqrt{1-x^{2}},\) so

\[\frac{d y}{d x}=\frac{1}{2}\left(1-x^{2}\right)^{-\frac{1}{2}}(-2 x)=-\frac{x}{\sqrt{1-x^{2}}} .\] Hence \[\sqrt{1+\left(\frac{d y}{d x}\right)^{2}}=\sqrt{1+\frac{x^{2}}{1-x^{2}}}=\sqrt{\frac{1-x^{2}+x^{2}}{1-x^{2}}}=\frac{1}{\sqrt{1-x^{2}}} .\] Hence, by \((2.5 .28)\), \[L=\int_{-\frac{1}{\sqrt{2}}}^{\frac{1}{\sqrt{2}}} \frac{1}{\sqrt{1-x^{2}}} d x .\] If we let \[\begin{aligned} x &=\sin (z) \\ d x &=\cos (z) d z, \end{aligned}\] then \[\begin{aligned} L &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{\sqrt{1-\sin ^{2}(z)}} \cos (z) d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{\cos (z)}{\sqrt{\cos ^{2}(z)}} d z \\ &=\int_{-\frac{\pi}{4}}^{-\frac{\pi}{4}} \frac{\cos (z)}{\cos (z)} d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d z \\ &=\frac{\pi}{2} . \end{aligned}\]

Exercise \(\PageIndex{26}\)

Use the change of variable \(x=2 \sin (z)\) to evaluate

\[\int_{-2}^{2} \sqrt{4-x^{2}} d x ,\]

Answer

\(\int_{-2}^{2} \sqrt{4-x^{2}} d x=2 \pi\)

Exercise \(\PageIndex{27}\)

Evaluate \(\int_{-2}^{1} \frac{2}{\sqrt{16-x^{2}}} d x\).

Answer

\(\int_{-2}^{2} \frac{2}{\sqrt{16-x^{2}}} d x=\frac{\pi}{6}\)

Example \(\PageIndex{19}\)

In Example 2.5.8 we saw that the arc length \(L\) of the parabola \(y=x^{2}\) over the interval \([0,1]\) is

\[L=\int_{0}^{1} \sqrt{1+4 x^{2}} d x .\] However, at that point we did not have the means to evaluate this integral. We now have most, although not all, of the necessary tools. To begin, we will first make the change of variable \[\begin{aligned} u &=2 x \\ d u &=2 d x, \end{aligned}\] which gives us \[L=\frac{1}{2} \int_{0}^{2} \sqrt{1+u^{2}} d u .\] Next, we recall the trigonometric identity \[1+\tan ^{2}(t)=\sec ^{2}(t)\] (a consequence of dividing each term of the identity \(\cos ^{2}(t)+\sin ^{2}(t)=1\) by \(\left.\cos ^{2}(t)\right),\) which is a hint that the change of variable \[\begin{aligned} x &=\tan (z) \\ d x &=\sec ^{2}(z) \end{aligned}\] might be of use. If we let \(\alpha\) be the angle for which \(\tan (\alpha)=2,\) with \(0<\alpha<\frac{\pi}{2}\), and note that \(\tan (0)=0\) and \[\sqrt{1+\tan ^{2}(z)}=\sqrt{\sec ^{2}(z)}=|\sec (z)|=\sec (z)\] (note that \(\left.\sec (z)>0 \text { since } 0 \leq z \leq \frac{\pi}{2}\right),\) then \[L=\frac{1}{2} \int_{0}^{\alpha} \sec (z) \sec ^{2}(z) d z=\frac{1}{2} \int_{0}^{\alpha} \sec ^{3}(z) d z .\] We may reduce the integral on the right using an integration by parts: Letting \[\begin{aligned} u &=\sec (z) d z & & d v=\sec ^{2}(z) d x \\ d u &=\sec (z) \tan (z) d z & & v=\tan (z) ,\end{aligned}\] we have \[\begin{aligned} \int_{0}^{\alpha} \sec ^{3}(z) d z &=\left.\sec (z) \tan (z)\right|_{0} ^{\alpha}-\int_{0}^{\alpha} \sec (z) \tan ^{2}(z) d z \\ &=\sec (\alpha) \tan (\alpha)-\int_{0}^{\alpha} \sec (z)\left(\sec ^{2}(z)-1\right) d z \\ &=2 \sqrt{5}-\int_{0}^{\alpha} \sec ^{3}(z) d z+\int_{0}^{\alpha} \sec (z) d z ,\end{aligned}\] where we have used the fact that \(\tan (\alpha)=2\) and \(1+\tan ^{2}(\alpha)=\sec ^{2}(z)\) to find that \(\sec (\alpha)=\sqrt{5} .\) It now follows that \[2 \int_{0}^{\alpha} \sec ^{3}(z) d z=2 \sqrt{5}+\int_{0}^{\alpha} \sec (z) d z ,\] and so \[\int_{0}^{\alpha} \sec ^{3}(z) d z=\sqrt{5}+\frac{1}{2} \int_{0}^{\alpha} \sec (z) d z .\] Hence \[L=\frac{\sqrt{5}}{2}+\frac{1}{4} \int_{0}^{\alpha} \sec (z) d z .\] For this reduced integral, we notice that \[\int_{0}^{\alpha} \sec (z) d z=\int_{0}^{\alpha} \sec (z) \frac{\sec (z)+\tan (z)}{\sec (z)+\tan (z)} d z=\int_{0}^{\alpha} \frac{\sec ^{2}(z)+\sec (z) \tan (z)}{\sec (z)+\tan (z)} d z ,\] and so the change of variable \[\begin{aligned} w &=\sec (z)+\tan (z) \\ d w &=\left(\sec (z) \tan (z)+\sec ^{2}(z)\right) d z \end{aligned}\] gives us \[\int_{0}^{\alpha} \sec (z) d z=\int_{1}^{2+\sqrt{5}} \frac{1}{w} d w .\] Thus we now have \[L=\frac{\sqrt{5}}{2}+\frac{1}{4} \int_{1}^{2+\sqrt{5}} \frac{1}{w} d w .\] Although greatly simplified from the integral with which we started, nevertheless we cannot evaluate the remaining integral with our current tools. Indeed, we may use the fundamental theorem of calculus to evaluate, for any rational number \(n,\) any definite integral involving \(w^{n},\) except in the very case we are facing now, that is, when \(n=-1 .\) We will fill in this gap in the next section, and finish this example at that time (see Example \(2.7 .9) .\)

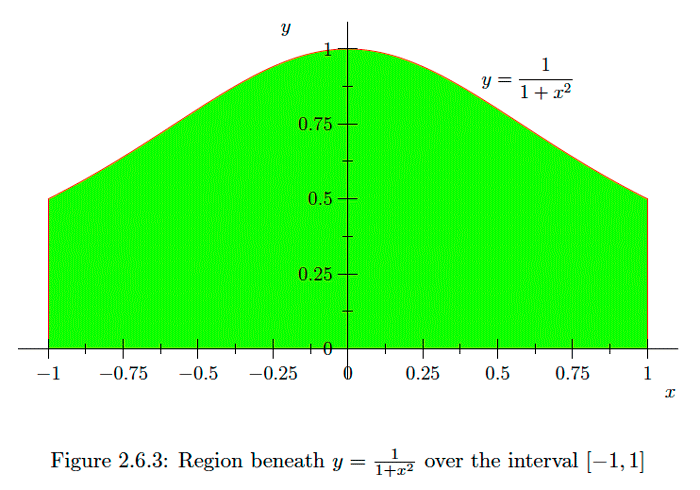
Example \(\PageIndex{20}\)

For a simpler example of the change of variable used in the previous example, consider the integral

\[\int_{-1}^{1} \frac{1}{1+x^{2}} d x ,\] the area under the curve \[y=\frac{1}{1+x^{2}}\] over the interval \([-1,1] \text { (see Figure } 2.6 .3) .\) If we let \[\begin{aligned} x &=\tan (z) \\ d x &=\sec ^{2}(z) d z, \end{aligned}\]

and note that \(\tan \left(-\frac{\pi}{4}\right)=-1\) and \(\tan \left(\frac{\pi}{4}\right)=1,\) then

\[\begin{aligned} \int_{-1}^{1} \frac{1}{1+x^{2}} d x &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{1}{1+\tan ^{2}(z)} \sec ^{2}(z) d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \frac{\sec ^{2}(z)}{\sec ^{2}(z)} d z \\ &=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} d z \\ &=\frac{\pi}{2}. \end{aligned}\] You should compare this with the simple approximation we saw in Example \(2.3 .1 .\)

Exercise \(\PageIndex{28}\)

Evaluate \(\int_{-3}^{3} \frac{6}{9+x^{2}} d x\).

Answer

\(\int_{-3}^{3} \frac{6}{9+x^{2}} d x=\pi\)

Exercise \(\PageIndex{29}\)

Evaluate \(\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{1}{1+4 x^{2}} d x\).

Answer

\(\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{1}{1+4 x^{2}} d x=\frac{\pi}{4}\)

Exercise \(\PageIndex{30}\)

Show that for any positive integer \(n>2\),

\[\int \sec ^{n}(x) d x=\frac{1}{n-1} \sec ^{n-2}(x) \tan (x)+\frac{n-2}{n-1} \int \sec ^{n-2}(x) d x.\]