Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.5: Work

Last updated

Feb 8, 2025
Save as PDF
- 9.4: Average Value of a Function
- 9.6: Center of Mass

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

A fundamental concept in classical physics is work: If an object is moved in a straight line against a force $F$ for a distance $s$ the work done is $W=Fs$ .

The force due to gravity on a 10 pound weight is 10 pounds at the surface of the earth, and it does not change appreciably over 5 feet. The work done is $W=10\cdot 5=50$ foot-pounds.

In reality few situations are so simple. The force might not be constant over the range of motion, as in the next example.

Over 100 miles the force due to gravity does change significantly, so we need to take this into account. The force exerted on a 10 pound weight at a distance $r$ from the center of the earth is $F=k/r^2$ and by definition it is 10 when $r$ is the radius of the earth (we assume the earth is a sphere). How can we approximate the work done? We divide the path from the surface to orbit into $n$ small subpaths. On each subpath the force due to gravity is roughly constant, with value $k/r_i^2$ at distance $r_i$ . The work to raise the object from $r_i$ to $r_{i+1}$ is thus approximately $k/r_i^2\Delta r$ and the total work is approximately $sum_{i=0}^{n-1} {k\over r_i^2}\Delta r,$ or in the limit $W=\int_{r_0}^{r_1} {k\over r^2}\,dr,$ where $r_0$ is the radius of the earth and $r_1$ is $r_0$ plus 100 miles. The work is $W=\int_{r_0}^{r_1} {k\over r^2}\,dr= -\left.{k\over r}\right|_{r_0}^{r_1}=-{k\over r_1}+{k\over r_0}.$ Using $r_0=20925525$ feet we have $r_1=21453525$ . The force on the 10 pound weight at the surface of the earth is 10 pounds, so $10=k/20925525^2$ , giving $k=4378775965256250$ . Then $-{k\over r_1}+{k\over r_0}={491052320000\over 95349}\approx 5150052 \quad\hbox{foot-pounds}.$ Note that if we assume the force due to gravity is 10 pounds over the whole distance we would calculate the work as $10(r_1-r_0)=10\cdot100\cdot 5280=5280000$ , somewhat higher since we don't account for the weakening of the gravitational force.

This is the same problem as before in different units, and we are not specifying a value for $D$ . As before $W=\int_{r_0}^{D} {k\over r^2}\,dr= -\left.{k\over r}\right|_{r_0}^{D}=-{k\over D}+{k\over r_0}.$ While "weight in pounds'' is a measure of force, "weight in kilograms'' is a measure of mass. To convert to force we need to use Newton's law $F=ma$ . At the surface of the earth the acceleration due to gravity is approximately 9.8 meters per second squared, so the force is $F=10\cdot 9.8=98$ . The units here are "kilogram-meters per second squared'' or "kg m/s $^2$ '', also known as a Newton (N), so $F=98$ N. The radius of the earth is approximately 6378.1 kilometers or 6378100 meters. Now the problem proceeds as before. From $F=k/r^2$ we compute $k$ : $98=k/6378100^2$ , $k= 3.986655642\cdot 10^{15}$ . Then the work is: $W=-{k\over D}+6.250538000\cdot 10^8\quad\hbox{Newton-meters.}$ As $D$ increases $W$ of course gets larger, since the quantity being subtracted, $-k/D$ , gets smaller. But note that the work $W$ will never exceed $6.250538000\cdot 10^8$ , and in fact will approach this value as $D$ gets larger. In short, with a finite amount of work, namely $6.250538000\cdot 10^8$ N-m, we can lift the 10 kilogram object as far as we wish from earth.

Next is an example in which the force is constant, but there are many objects moving different distances.

Here we have a large number of atoms of water that must be lifted different distances to get to the top of the tank. Fortunately, we don't really have to deal with individual atoms---we can consider all the atoms at a given depth together. To approximate the work, we can divide the water in the tank into horizontal sections, approximate the volume of water in a section by a thin disk, and compute the amount of work required to lift each disk to the top of the tank. As usual, we take the limit as the sections get thinner and thinner to get the total work.

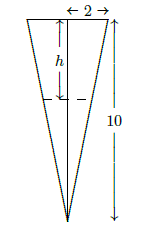
$Cross-section of a conical water tank.$
Figure 9.5.1. Cross-section of a conical water tank.

At depth $h$ the circular cross-section through the tank has radius $r=(10-h)/5$ , by similar triangles, and area $\pi(10-h)^2/25$ . A section of the tank at depth $h$ thus has volume approximately $\pi(10-h)^2/25\Delta h$ and so contains $\sigma\pi(10-h)^2/25\Delta h$ kilograms of water, where $\sigma$ is the density of water in kilograms per cubic meter; $\sigma\approx 1000$ . The force due to gravity on this much water is $9.8\sigma\pi(10-h)^2/25\Delta h$ , and finally, this section of water must be lifted a distance $h$ , which requires $h9.8\sigma\pi(10-h)^2/25\Delta h$ Newton-meters of work. The total work is therefore

$W={9.8\sigma\pi\over 25} \int_0^{10} h(10-h)^2\,dh={980000\over3}\pi\approx 1026254\quad\hbox{Newton-meters.}$

A spring has a "natural length,'' its length if nothing is stretching or compressing it. If the spring is either stretched or compressed the spring provides an opposing force; according to Hooke's Law the magnitude of this force is proportional to the distance the spring has been stretched or compressed: $F=kx$ . The constant of proportionality, $k$ , of course depends on the spring. Note that $x$ here represents the change in length from the natural length.

Assuming that the constant $k$ has appropriate dimensions (namely, kg/s $^2$ ), the force is $5(0.1-0.08)=5(0.02)=0.1$ Newtons.

We can approximate the work by dividing the distance that the spring is compressed (or stretched) into small subintervals. Then the force exerted by the spring is approximately constant over the subinterval, so the work required to compress the spring from $x_i$ to $x_{i+1}$ is approximately $5(x_i-0.1)\Delta x$ . The total work is approximately $sum_{i=0}^{n-1} 5(x_i-0.1)\Delta x$ and in the limit $W=\int_{0.1}^{0.08} 5(x-0.1)\,dx=\left.{5(x-0.1)^2\over2}\right|_{0.1}^{0.08}= {5(0.08-0.1)^2\over2}-{5(0.1-0.1)^2\over2}={1\over1000}\,\hbox{N-m}.$ The other values we seek simply use different limits. To compress the spring from $0.08$ meters to $0.05$ meters takes $W=\int_{0.08}^{0.05} 5(x-0.1)\,dx=\left.{5x^2\over2}\right|_{0.08}^{0.05}= {5(0.05-0.1)^2\over2}-{5(0.08-0.1)^2\over2}={21\over4000}\quad\hbox{N-m}$ and to stretch the spring from $0.1$ meters to $0.15$ meters requires $W=\int_{0.1}^{0.15} 5(x-0.1)\,dx=\left.{5x^2\over2}\right|_{0.1}^{0.15}= {5(0.15-0.1)^2\over2}-{5(0.1-0.1)^2\over2}={1\over160}\quad\hbox{N-m}.$

Contributors and Attributions

David Guichard (Whitman College)
Integrated by Justin Marshall.

The force due to gravity on a 10 pound weight is 10 pounds at the surface of the earth, and it does not change appreciably over 5 feet. The work done is W=10⋅5=50W=10\cdot 5=50 foot-pounds.

Assuming that the constant kk has appropriate dimensions (namely, kg/s2^2), the force is 5(0.1−0.08)=5(0.02)=0.15(0.1-0.08)=5(0.02)=0.1 Newtons.

Contributors and Attributions

Support Center

How can we help?

The force due to gravity on a 10 pound weight is 10 pounds at the surface of the earth, and it does not change appreciably over 5 feet. The work done is $W=10\cdot 5=50$ foot-pounds.

Assuming that the constant $k$ has appropriate dimensions (namely, kg/s $^2$ ), the force is $5(0.1-0.08)=5(0.02)=0.1$ Newtons.