5.8: Exercises

5.1. Equation of tangent line. Find the equation of the tangent line to the function \(y=f(x)=|x+1|\) at:

(a) \(x=-1\)

(b) \(x=-2\)

(c) \(x=0\)

If there is a problem finding a tangent line at one of these points, indicate what the problem is.

5.2. Equation of tangent line. A function \(f(x)\) satisfies \(f(1)=-1\) and \(f^{\prime}(1)=2\). What is the equation of the tangent line of \(f(x)\) at \(x=\) 1 ?

5.3. Point of tangency. Shown in Figure \(5.13\) is the graph of \(y=x^{2}\) with one of its tangent lines.

Figure 5.13: Figure for Exercise 5.3; \(y=x^{2}\) and a point of tangency.

(a) Show that the slope of the tangent to the curve \(y=x^{2}\) at the point \(x=a\) is \(2 a\).

(b) Suppose that the tangent line intersects the \(x\) axis at the point \((1,0)\). Find the coordinate, \(a\), of the point of tangency.

5.4. Approximation with a tangent line. Shown in Figure \(5.14\) is the function \(f(x)=1 / x^{4}\) together with its tangent line at \(x=1\).

Figure 5.14: Figure for Exercise 5.4; \(f(x)=\frac{1}{x^{4}}\) and a point of tangency.

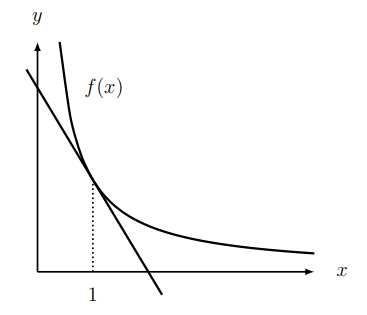
(a) Find the equation of the tangent line.

(b) Determine the points of intersection of the tangent line with the \(x\) and the \(y\)-axes.

(c) Use the tangent line to obtain a linear approximation to the value of \(f(1.1)\). Is this approximation larger or smaller than the actual value of the function at \(x=1.1\) ?

5.5. Linear approximation. Shown in Figure \(5.15\) is the function \(f(x)=\) \(x^{3}\) with a tangent line at the point \((1,1)\).

Figure 5.15: Figure for Exercise 5.5; \(f(x)=x^{3}\) and a point of tangency.

(a) Find the equation of the tangent line.

(b) Determine the point at which the tangent line intersects the \(x\) axis.

(c) Compute the value of the function at \(x=1.1\). Compare this with the value of \(y\) on the tangent line at \(x=1.1\).

This latter value is the linear approximation of the function at the desired point based on its known value and known derivative at the nearby point \(x=1\).

5.6. Generic tangent line. Shown in Figure \(5.16\) is the graph of a function and its tangent line at the point \(x_{0}\).

Figure 5.16: Figure for Exercise 5.6; generic function and tangent line.

(a) Find the equation of the tangent line expressed in terms of \(x_{0}, f\left(x_{0}\right)\) and \(f^{\prime}\left(x_{0}\right)\).

(b) Find the coordinate \(x_{1}\) at which the tangent line intersects the \(x\) axis.

5.7. Estimating a square root. Use Newton’s method to find an approximate value for \(\sqrt{8}\) (hint: first think of a function, \(f(x)\), such that \(f(x)=0\) has the solution \(x=\sqrt{8})\).

5.8. Finding points of intersection. Find the point(s) of intersection of: \(y_{1}=8 x^{3}-10 x^{2}+x+2\) and \(y_{2}=x^{3}+15 x^{2}-x-4\) (hint: an intersection point exists between \(x=3\) and \(x=4\) ).

5.9. Roots of cubic equations. Find the roots for each of the following cubic equations using Newton’s method:

(a) \(x^{3}+3 x-1=0\)

(b) \(x^{3}+x^{2}+x-2=0\)

(c) \(x^{3}+5 x^{2}-2=0\) (hint: find an approximation to a first root \(a\) using Newton’s method, then divide the left hand side of the equation by \((x-a)\) to obtain a quadratic equation, which can be solved by the quadratic formula).

5.10. Intersecting tangent lines. The parabola \(y=x^{2}\) has two tangent lines that intersect at the point \((2,3)\). These are shown as the dark lines in Figure 5.17. Find the coordinates of the two points at which the lines are tangent to the parabola.

Figure 5.17: Figure for Exercise 5.10; \(y=x^{2}\)

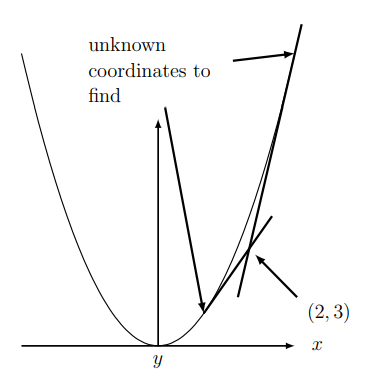
Note: note that the point \((2,3)\) is not on the parabola.

5.11. An approximation for the square root. Use a linear approximation to find a rough estimate of the following functions at the indicated points.

(a) \(y=\sqrt{x}\) at \(x=10\) (use the fact that \(\sqrt{9}=3\) ).

(b) \(y=5 x-2\) at \(x=1\).

5.12. An approximation for the cube root. Use the method of linear approximation to find the cube root of

(a) \(0.065\) (hint: \(\sqrt[3]{0.064}=0.4)\)

(b) 215 (hint: \(\sqrt[3]{216}=6\) )

5.13. Approximating from a graph. Use the data in the graph in Figure \(5.18\) to make the best approximation you can to \(f(2.01)\).

Figure 5.18: Figure for Exercise 5.13; using a graph to approximate the value of a function.

5.14. Linear approximation. Approximate the value of \(f(x)=x^{3}-2 x^{2}+\) \(3 x-5\) at \(x=1.001\) using the method of linear approximation.

5.15. Approximating cube volume. Approximate the volume of a cube whose length of each side is \(10.1 \mathrm{~cm}\).

5.16. Using Newton’s method to find a critical point. Consider the function \[g(x)=x^{5}-4 x^{4}+3 x^{3}+x^{2}-3 x . \nonumber \]

Critical points of a function are defined as values of \(x\) for which \(g^{\prime}(x)=0\). However, for this fifth order polynomial, it is not easy to find such points analytically (i.e., using pencil and paper).

(a) Use Newton’s Method to find a critical point for positive values of \(x\). Find an initial approximation for the critical point by plotting the function, but use a spreadsheet and explain how you set up the calculations. Provide an answer accurate to 8 decimal points.

(b) Explain why a starting value of \(x_{0}=1\) for Newton’s Method does not lead to the positive critical point. You may support your argument with a graph.

Note: in Section \(6.2\) we study critical points in greater depth.

5.17. Newton’s Method Use Newton’s method to find a decimal approximation of the value of \(\sqrt{105}\) correct to 16 decimal points.