10E: Derivatives of Multivariable Functions
- Page ID
- 108399
10.1: Limits
Find the limits, if they exist, or type DNE for any which do not exist.
1) Along the \(x\)-axis:
2) Along the \(y\)-axis:
3) Along the line \(y=mx\) :
4) The limit is:
\(0.333333333333333\)
\(0\)
\(\frac{1}{3+4m^{2}}\)
dne
In this problem we show that the function
does not have a limit as \((x,y)\to (0,0)\text{.}\)
(a) Suppose that we consider \((x,y)\to (0,0)\) along the curve \(y = 4 x\text{.}\) Find the limit in this case:
\(\lim\limits_{(x,4 x)\to(0,0)} \frac{6x-y}{x+y} =\)
(b) Now consider \((x,y)\to (0,0)\) along the curve \(y = 5 x\text{.}\) Find the limit in this case:
\(\lim\limits_{(x,5 x)\to(0,0)} \frac{6x-y}{x+y} =\)
(c) Note that the results from (a) and (b) indicate that \(f\) has no limit as \((x,y)\to (0,0)\) (be sure you can explain why!).
To show this more generally, consider \((x,y)\to (0,0)\) along the curve \(y = m x\text{,}\) for arbitrary \(m\text{.}\) Find the limit in this case:
\(\lim\limits_{(x,m x)\to(0,0)} \frac{6x-y}{x+y} =\)
(Be sure that you can explain how this result also indicates that \(f\) has no limit as \((x,y)\to(0,0)\text{.}\)
\(\frac{6-4^{1}}{1+4^{1}}\)
\(\frac{6-5^{1}}{1+5^{1}}\)
\(\frac{6-m}{1+m}\)
Show that the function
does not have a limit at \((0,0)\) by examining the following limits.
(a) Find the limit of \(f\) as \((x,y) \to (0,0)\) along the line \(y = x\text{.}\)
\(\lim\limits_{^{(x,y) \to (0,0)}_{y=x}} f(x,y) =\)
(b) Find the limit of \(f\) as \((x,y)\to(0,0)\) along the curve \(y = x^3\text{.}\)
\(\lim\limits_{^{(x,y)\to(0,0)}_{y=x^3}} f(x,y) =\)
(Be sure that you are able to explain why the results in (a) and (b) indicate that \(f\) does not have a limit at (0,0)!
\(0\)
\(1\)
Find the limit, if it exists, or type N if it does not exist.
\(\displaystyle \lim_{(x, y) \rightarrow (0, 0)} \frac{3 x^2}{ 3 x^2 + 5 y^2} =\)
\(\text{N}\)
Find the limit, if it exists, or type N if it does not exist.
\(\displaystyle \lim_{(x, y) \rightarrow (0, 0)} \frac{(x + 13y)^2}{x^2 + {13}^2y^2} =\)
\(\text{N}\)
Find the limit, if it exists, or type 'DNE' if it does not exist.
\(\displaystyle \lim_{(x, y) \rightarrow (1, 3)} e^{\sqrt{4x^2 + 3y^2}} =\)
\(261.848047157352\)
Find the limit, if it exists, or type N if it does not exist.
\(\displaystyle \lim_{(x, y, z) \rightarrow (0, 0, 0)} \frac{4 xy+ 2 yz+ 2 xz }{16 x^2+ 4 y^2+ 4 z^2} =\)
\(\text{N}\)
Find the limit, if it exists, or type N if it does not exist.
\(\displaystyle \lim_{(x, y, z) \rightarrow (5, 1, 4)} \frac{2 z e^{x^2+y^2}}{5 x^2+ y^2+ 4 z^2} =\)
\(8241246712.79321\)
Find the limit (enter 'DNE' if the limit does not exist)
Hint: rationalize the denominator.
\(2\)
The largest set on which the function \(f(x,y) = 1/(3 - x^2 - y^2)\) is continuous is
- All of the xy-plane
- The interior of the circle \(x^2 + y^2 = 3\)
- The exterior of the circle \(x^2 + y^2 = 3\)
- The interior of the circle \(x^2 + y^2 = 3\text{,}\) plus the circle
- All of the xy-plane except the circle \(x^2 + y^2 = 3\)
E
Consider the function \(f\) defined by \(f(x,y) = \frac{xy}{x^2 + y^2 + 1}.\)
- What is the domain of \(f\text{?}\)
- Evaluate limit of \(f\) at \((0,0)\) along the following paths: \(x = 0\text{,}\) \(y = 0\text{,}\) \(y = x\text{,}\) and \(y = x^2\text{.}\)
- What do you conjecture is the value of \(\lim_{(x,y) \to (0,0)} f(x,y)\text{?}\)
- Is \(f\) continuous at \((0,0)\text{?}\) Why or why not?
- Use appropriate technology to sketch both surface and contour plots of \(f\) near \((0,0)\text{.}\) Write several sentences to say how your plots affirm your findings in (a) - (d).
Consider the function \(g\) defined by \(g(x,y) = \frac{xy}{x^2 + y^2}.\)
- What is the domain of \(g\text{?}\)
- Evaluate limit of \(g\) at \((0,0)\) along the following paths: \(x = 0\text{,}\) \(y = x\text{,}\) and \(y = 2x\text{.}\)
- What can you now say about the value of \(\lim_{(x,y) \to (0,0)} g(x,y)\text{?}\)
- Is \(g\) continuous at \((0,0)\text{?}\) Why or why not?
- Use appropriate technology to sketch both surface and contour plots of \(g\) near \((0,0)\text{.}\) Write several sentences to say how your plots affirm your findings in (a) - (d).
Consider the function \(h\) defined by \(h(x,y) = \frac{2x^2y}{x^4 + y^2}.\)
- What is the domain of \(h\text{?}\)
- Evaluate the limit of \(h\) at \((0,0)\) along all linear paths the contain the origin. What does this tell us about \(\lim_{(x,y) \to (0,0)} h(x,y)\text{?}\) (Hint: A non-vertical line throught the origin has the form \(y = mx \) for some constant \(m\text{.}\))
- Does \(\lim_{(x,y) \to (0,0)} h(x,y)\) exist? Verify your answer. Check by using appropriate technology to sketch both surface and contour plots of \(h\) near \((0,0)\text{.}\) Write several sentences to say how your plots affirm your findings about \(\lim_{(x,y) \to (0,0)} h(x,y)\text{.}\)
For each of the following prompts, provide an example of a function of two variables with the desired properties (with justification), or explain why such a function does not exist.
- A function \(p\) that is defined at \((0,0)\text{,}\) but \(\lim_{(x,y) \to (0,0)} p(x,y)\) does not exist.
- A function \(q\) that does not have a limit at \((0,0)\text{,}\) but that has the same limiting value along any line \(y = mx\) as \(x \to 0\text{.}\)
- A function \(r\) that is continuous at \((0,0)\text{,}\) but \(\lim_{(x,y) \to (0,0)} r(x,y)\) does not exist.
- A function \(s\) such that
\[ \lim_{(x,x) \to (0,0)} s(x,x) = 3 \ \ \ \mbox{and} \ \ \ \lim_{(x,2x) \to (0,0)} s(x,2x) = 6, \nonumber \]
for which \(\lim_{(x,y) \to (0,0)} s(x,y)\) exists.
- A function \(t\) that is not defined at \((1,1)\) but \(\lim_{(x,y) \to (1,1)} t(x,y)\) does exist.
Use the properties of continuity to determine the set of points at which each of the following functions is continuous. Justify your answers.
- The function \(f\) defined by \(f(x,y) = \frac{x+2y}{x-y}\)
- The function \(g\) defined by \(g(x,y) = \frac{\sin(x)}{1+e^y}\)
- The function \(h\) defined by
\[ h(x,y) = \begin{cases} \frac{xy}{x^2+y^2} & \text{ if } (x,y) \neq (0,0) \\[4pt] 0 & \text{ if } (x,y) = (0,0) \end{cases} \nonumber \]
- The function \(k\) defined by
\[ k(x,y) = \begin{cases} \frac{x^2y^4}{x^2+y^2} & \text{ if } (x,y) \neq (0,0) \\[4pt] 0 & \text{ if } (x,y) = (0,0) \end{cases} \nonumber \]
10.2: First-Order Partial Derivatives
Find the first partial derivatives of
\(\displaystyle f(x,y) = \frac{x - 4y}{x + 4y}\) at the point \((x,y) = (4, 1)\text{.}\)
\(\displaystyle \frac{\partial f}{\partial x}(4, 1) =\)
\(\displaystyle \frac{\partial f}{\partial y}(4, 1) =\)
\(0.125\)
\(-0.5\)
Find the first partial derivatives of \(f(x, y) = \sin(x - y)\) at the point (-4, -4).
A. \(f_x(-4, -4) =\)
B. \(f_y(-4, -4) =\)
\(1\)
\(-1\)
Find the partial derivatives of the function
\(\frac{\partial w}{\partial r} =\)
\(\frac{\partial w}{\partial s} =\)
\(\frac{\partial w}{\partial t} =\)
\(\frac{4r}{\sqrt{4r^{2}+3s^{2}+7t^{2}}}\)
\(\frac{3s}{\sqrt{4r^{2}+3s^{2}+7t^{2}}}\)
\(\frac{7t}{\sqrt{4r^{2}+3s^{2}+7t^{2}}}\)
Suppose that \(f(x,y)\) is a smooth function and that its partial derivatives have the values, \(f_x(0, 9) = -4\) and \(f_y(0, 9) = -2\text{.}\) Given that \(f(0, 9) = 1\text{,}\) use this information to estimate the value of \(f(1, 10)\text{.}\) Note this is analogous to finding the tangent line approximation to a function of one variable. In fancy terms, it is the first Taylor approximation.
Estimate of (integer value) \(f(0, 10)\)
Estimate of (integer value) \(f(1, 9)\)
Estimate of (integer value) \(f(1, 10)\)
\(-1\)
\(-3\)
\(-5\)
The gas law for a fixed mass \(m\) of an ideal gas at absolute temperature \(T\text{,}\) pressure \(P\text{,}\) and volume \(V\) is \(PV = mRT\text{,}\) where \(R\) is the gas constant.
Find the partial derivatives
\(\displaystyle \frac{\partial P}{\partial V} =\)
\(\displaystyle \frac{\partial V}{\partial T} =\)
\(\displaystyle \frac{\partial T}{\partial P} =\)
\(\displaystyle \frac{\partial P}{\partial V} \frac{\partial V}{\partial T}\frac{\partial T}{\partial P} =\) (an integer)
\(\frac{-mRT}{V^{2}}\)
\(\frac{mR}{P}\)
\(\frac{V}{mR}\)
\(-1\)
Find the first partial derivatives of \(f(x,y,z) = z \ \arctan(\frac{y}{x})\) at the point (4, 4, -3).
A. \(\frac{\partial f}{\partial x}(4, 4, -3) =\)
B. \(\frac{\partial f}{\partial y}(4, 4, -3) =\)
C. \(\frac{\partial f}{\partial z}(4, 4, -3) =\)
\(0.375\)
\(-0.375\)
\(0.785398163397448\)
Find the partial derivatives of the function
\(f_x(x,y) =\)
\(f_y(x,y) =\)
\(\cos\!\left(7x^{2}+8x+\left(-2\right)\right)\)
\(-\cos\!\left(7y^{2}+8y+\left(-2\right)\right)\)
Let \(f(x,y) = e^{-2x}\sin\!\left(4y\right)\text{.}\)
(a) Using difference quotients with \(\Delta x = 0.1\) and \(\Delta y = 0.1\text{,}\) we estimate
\(f_x (2, -2) \approx\)
\(f_y (2, -2) \approx\)
(b) Using difference quotients with \(\Delta x = 0.01\) and \(\Delta y = 0.01\text{,}\) we find better estimates:
\(f_x (2, -2) \approx\)
\(f_y (2, -2) \approx\)
\(0.0328473\)
\(0.00392661\)
\(0.0358814\)
\(-0.0092074\)
Determine the sign of \(f_x\) and \(f_y\) at each indicated point using the contour diagram of \(f\) shown below. (The point \(P\) is that in the first quadrant, at a positive \(x\) and \(y\) value; \(Q\) through \(T\) are located clockwise from \(P\text{,}\) so that \(Q\) is at a positive \(x\) value and negative \(y\text{,}\) etc.)
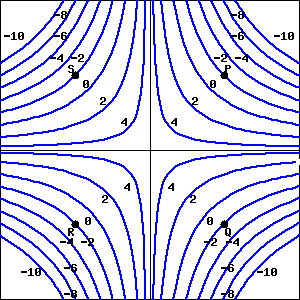

(a) At point \(P\text{,}\)
\(f_x\) is
- positive
- negative
\(f_y\) is
- positive
- negative
(b) At point \(Q\text{,}\)
\(f_x\) is
- positive
- negative
\(f_y\) is
- positive
- negative
(c) At point \(S\text{,}\)
\(f_x\) is
- positive
- negative
\(f_y\) is
- positive
- negative
\(\text{negative}\)
\(\text{negative}\)
\(\text{negative}\)
\(\text{positive}\)
\(\text{positive}\)
\(\text{negative}\)
Your monthly car payment in dollars is \(P = f(P_0,t,r)\text{,}\) where $\(P_0\) is the amount you borrowed, \(t\) is the number of months it takes to pay off the loan, and \(r\) percent is the interest rate.
(a) Is \(\partial P /\partial t\) positive or negative?
- positive
- negative
Suppose that your bank tells you that the magnitude of \(\partial P /\partial t\) is 15.
What are the units of this value?
(For this problem, write our your units in full, writing dollars for $, months for months, percent for %, etc. Note that fractional units generally have a plural numerator and singular denominator.)
(b) Is \(\partial P /\partial r\) positive or negative?
- positive
- negative
Suppose that your bank tells you that the magnitude of \(\partial P /\partial r\) is 25.
What are the units of this value?
(For this problem, write our your units in full, writing dollars for $, months for months, percent for %, etc. Note that fractional units generally have a plural numerator and singular denominator.)
For both parts of this problem, be sure you can explain what the practical meanings of the partial derivatives are.
\(\text{negative}\)
\({\text{dollars/month}}\)
\(\text{positive}\)
\({\text{dollars/percent}}\)
An experiment to measure the toxicity of formaldehyde yielded the data in the table below. The values show the percent, \(P=f(t,c)\text{,}\) of rats surviving an exposure to formaldehyde at a concentration of \(c\) (in parts per million, ppm) after \(t\) months.
| \(t=14\) | \(t=16\) | \(t=18\) | \(t=20\) | \(t=22\) | \(t=24\) | |
|---|---|---|---|---|---|---|
| \(c=0\) | 100 | 100 | 100 | 99 | 97 | 95 |
| \(c=2\) | 100 | 99 | 98 | 97 | 95 | 92 |
| \(c=6\) | 96 | 95 | 93 | 90 | 86 | 80 |
| \(c=15\) | 96 | 93 | 82 | 70 | 58 | 36 |
(a) Estimate \(f_t(18,6)\text{:}\)
\(f_t(18, 6)\approx\)
(b) Estimate \(f_c(18,6)\text{:}\)
\(f_c(18, 6)\approx\)
(Be sure that you can give the practical meaning of these two values in terms of formaldehyde toxicity.)
\(\frac{90-95}{20-16}\)
\(\frac{82-98}{15-2}\)
An airport can be cleared of fog by heating the air. The amount of heat required depends on the air temperature and the wetness of the fog. The figure below shows the heat \(H(T,w)\) required (in calories per cubic meter of fog) as a function of the temperature \(T\) (in degrees Celsius) and the water content \(w\) (in grams per cubic meter of fog). Note that this figure is not a contour diagram, but shows cross-sections of \(H\) with \(w\) fixed at \(0.1\text{,}\) \(0.2\text{,}\) \(0.3\text{,}\) and \(0.4\text{.}\)
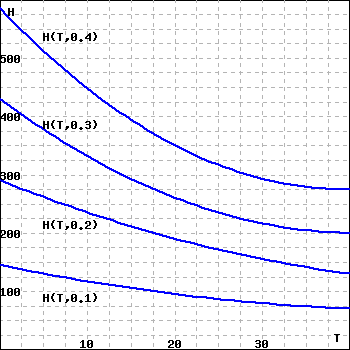

(a) Estimate \(H_T(10, 0.2)\text{:}\)
\(H_T(10,0.2) \approx\)
(Be sure you can interpret this partial derivative in practical terms.)
(b) Make a table of values for \(H(T,w)\) from the figure, and use it to estimate \(H_T(T,w)\) for each of the following:
\(T = 10, w = 0.2\) : \(H_T(T,w) \approx\)
\(T = 20, w = 0.2\) : \(H_T(T,w) \approx\)
\(T = 10, w = 0.3\) : \(H_T(T,w) \approx\)
\(T = 20, w = 0.3\) : \(H_T(T,w) \approx\)
(c) Repeat (b) to find \(H_w(T,w)\) for each of the following:
\(T = 10, w = 0.2\) : \(H_w(T,w) \approx\)
\(T = 20, w = 0.2\) : \(H_w(T,w) \approx\)
\(T = 10, w = 0.3\) : \(H_w(T,w) \approx\)
\(T = 20, w = 0.3\) : \(H_w(T,w) \approx\)
(Be sure you can interpret this partial derivative in practical terms.)
\(\frac{190-240}{10}\)
\(\frac{190-240}{10}\)
\(\frac{160-190}{10}\)
\(\frac{260-330}{10}\)
\(\frac{220-260}{10}\)
\(\frac{330-240}{0.1}\)
\(\frac{260-190}{0.1}\)
\(\frac{450-330}{0.1}\)
\(\frac{350-260}{0.1}\)
The Heat Index, \(I\text{,}\) (measured in apparent degrees F) is a function of the actual temperature \(T\) outside (in degrees F) and the relative humidity \(H\) (measured as a percentage). A portion of the table which gives values for this function, \(I=I(T,H)\text{,}\) is reproduced in Table 10.2.10.
| T \(\downarrow \backslash\) H \(\rightarrow\) | 70 | 75 | 80 | 85 |
|---|---|---|---|---|
| 90 | 106 | 109 | 112 | 115 |
| 92 | 112 | 115 | 119 | 123 |
| 94 | 118 | 122 | 127 | 132 |
| 96 | 125 | 130 | 135 | 141 |
- State the limit definition of the value \(I_T(94,75)\text{.}\) Then, estimate \(I_T(94,75)\text{,}\) and write one complete sentence that carefully explains the meaning of this value, including its units.
- State the limit definition of the value \(I_H(94,75)\text{.}\) Then, estimate \(I_H(94,75)\text{,}\) and write one complete sentence that carefully explains the meaning of this value, including its units.
- Suppose you are given that \(I_T(92,80) = 3.75\) and \(I_H(92,80) = 0.8\text{.}\) Estimate the values of \(I(91,80)\) and \(I(92,78)\text{.}\) Explain how the partial derivatives are relevant to your thinking.
- On a certain day, at 1 p.m. the temperature is 92 degrees and the relative humidity is 85%. At 3 p.m., the temperature is 96 degrees and the relative humidity 75%. What is the average rate of change of the heat index over this time period, and what are the units on your answer? Write a sentence to explain your thinking.
Let \(f(x,y) = \frac{1}{2}xy^2\) represent the kinetic energy in Joules of an object of mass \(x\) in kilograms with velocity \(y\) in meters per second. Let \((a,b)\) be the point \((4,5)\) in the domain of \(f\text{.}\)
- Calculate \(f_x(a,b)\text{.}\)
- Explain as best you can in the context of kinetic energy what the partial derivative
\[ f_x(a,b) = \lim_{h \to 0} \frac{f(a+h,b) - f(a,b)}{h} \nonumber \]
tells us about kinetic energy.
- Calculate \(f_y(a,b)\text{.}\)
- Explain as best you can in the context of kinetic energy what the partial derivative
\[ f_y(a,b) = \lim_{h \to 0} \frac{f(a,b+h) - f(a,b)}{h} \nonumber \]
tells us about kinetic energy.
- Often we are given certain graphical information about a function instead of a rule. We can use that information to approximate partial derivatives. For example, suppose that we are given a contour plot of the kinetic energy function (as in Figure 10.2.11) instead of a formula. Use this contour plot to approximate \(f_x(4,5)\) and \(f_y(4,5)\) as best you can. Compare to your calculations from earlier parts of this exercise.
-
Figure 10.2.11. The graph of \(f(x,y) = \frac{1}{2}xy^2\text{.}\)
The temperature on an unevenly heated metal plate positioned in the first quadrant of the \(xy\)-plane is given by
Assume that temperature is measured in degrees Celsius and that \(x\) and \(y\) are each measured in inches. (Note: At no point in the following questions should you expand the denominator of \(C(x,y)\text{.}\))
- Determine \(\frac{\partial C}{\partial x}|_{(x,y)}\) and \(\frac{\partial C}{\partial y}|_{(x,y)}\text{.}\)
- If an ant is on the metal plate, standing at the point \((2,3)\text{,}\) and starts walking in the direction parallel to the positive \(y\) axis, at what rate will the temperature the ant is experiencing change? Explain, and include appropriate units.
- If an ant is walking along the line \(y = 3\) in the positive \(x\) direction, at what instantaneous rate will the temperature the ant is experiencing change when the ant passes the point \((1,3)\text{?}\)
- Now suppose the ant is stationed at the point \((6,3)\) and walks in a straight line towards the point \((2,0)\text{.}\) Determine the average rate of change in temperature (per unit distance traveled) the ant encounters in moving between these two points. Explain your reasoning carefully. What are the units on your answer?
Consider the function \(f\) defined by \(f(x,y) = 8 - x^2 - 3y^2\text{.}\)
- Determine \(f_x(x,y)\) and \(f_y(x,y)\text{.}\)
- Find parametric equations in \(\mathbb{R}^3\) for the tangent line to the trace \(f(x,1)\) at \(x=2\text{.}\)
- Find parametric equations in \(\mathbb{R}^3\) for the tangent line to the trace \(f(2,y)\) at \(y=1\text{.}\)
- State respective direction vectors for the two lines determined in (b) and (c).
- Determine the equation of the plane that passes through the point \((2,1,f(2,1))\) whose normal vector is orthogonal to the direction vectors of the two lines found in (b) and (c).
- Use a graphing utility to plot both the surface \(z = 8 - x^2 - 3y^2\) and the plane from (e) near the point \((2,1)\text{.}\) What is the relationship between the surface and the plane?
Recall from single variable calculus that, given the derivative of a single variable function and an initial condition, we can integrate to find the original function. We can sometimes use the same process for functions of more than one variable. For example, suppose that a function \(f\) satisfies \(f_x(x,y) = \cos(y)e^x+2x+y^2\text{,}\) \(f_y(x,y) = -\sin(y)e^x+2xy+3\text{,}\) and \(f(0,0) = 5\text{.}\)
- Find all possible functions \(f\) of \(x\) and \(y\) such that \(f_x(x,y) = \cos(y)e^x+2x+y^2\text{.}\) Your function will have both \(x\) and \(y\) as independent variables and may also contain summands that are functions of \(y\) alone.
- Use the fact that \(f_y(x,y) = -\sin(y)e^x+2xy+3\) to determine any unknown non-constant summands in your result from part (a).
- Complete the problem by determining the specific function \(f\) that satisfies the given conditions.
10.3: Second-Order Partial Derivatives
Exercises 10.3.4 Exercises
Calculate all four second-order partial derivatives of \(\displaystyle f(x,y) = 4x^{2}y+8xy^{3}\text{.}\)
\(f_{xx} \, (x,y) =\)
\(f_{xy} \, (x,y) =\)
\(f_{yx} \, (x,y) =\)
\(f_{yy} \, (x,y) =\)
\(8y\)
\(4\cdot 2x+8\cdot 3y^{2}\)
\(4\cdot 2x+8\cdot 3y^{2}\)
\(8x\cdot 3\cdot 2y\)
Find all the first and second order partial derivatives of \(f(x, y) = 3\sin(2x+y) - 4\cos(x-y)\text{.}\)
A. \(\frac{\partial f}{\partial x} = f_x =\)
B. \(\frac{\partial f}{\partial y} = f_y =\)
C. \(\frac{{\partial^2}f}{\partial x^2} = f_x{}_x =\)
D. \(\frac{{\partial^2}f}{\partial y^2} = f_y{}_y =\)
E. \(\frac{{\partial^2}f}{\partial x \partial y} = f_y{}_x =\)
F. \(\frac{{\partial^2}f}{\partial y \partial x} = f_x{}_y =\)
\(6\cos\!\left(2x+y\right)-\left(-4\right)\sin\!\left(x-y\right)\)
\(3\cos\!\left(2x+y\right)+\left(-4\right)\sin\!\left(x-y\right)\)
\(-4\cdot 3\sin\!\left(2x+y\right)-\left(-4\right)\cos\!\left(x-y\right)\)
\(-3\sin\!\left(2x+y\right)-\left(-4\right)\cos\!\left(x-y\right)\)
\(-2\cdot 3\sin\!\left(2x+y\right)+\left(-4\right)\cos\!\left(x-y\right)\)
\(-2\cdot 3\sin\!\left(2x+y\right)+\left(-4\right)\cos\!\left(x-y\right)\)
Find the partial derivatives of the function
\(f_x(x,y) =\)
\(f_y(x,y) =\)
\(f_{xy}(x,y) =\)
\(f_{yx}(x,y) =\)
\(y\exp\!\left(4y\right)\)
\(x\!\left(4y\exp\!\left(4y\right)+\exp\!\left(4y\right)\right)\)
\(4y\exp\!\left(4y\right)+\exp\!\left(4y\right)\)
\(4y\exp\!\left(4y\right)+\exp\!\left(4y\right)\)
Calculate all four second-order partial derivatives of \(\displaystyle f(x,y) = \sin\!\left(\frac{5x}{y}\right)\text{.}\)
\(f_{xx} \, (x,y) =\)
\(f_{xy} \, (x,y) =\)
\(f_{yx} \, (x,y) =\)
\(f_{yy} \, (x,y) =\)
\(-\frac{5y}{y^{2}}\frac{5y}{y^{2}}\sin\!\left(\frac{5x}{y}\right)\)
\(\frac{5y^{2}-5y\cdot 2y}{\left(y^{2}\right)^{2}}\cos\!\left(\frac{5x}{y}\right)+\frac{5y}{y^{2}}\frac{5x}{y^{2}}\sin\!\left(\frac{5x}{y}\right)\)
\(-\left(\frac{5y^{2}}{\left(y^{2}\right)^{2}}\cos\!\left(\frac{5x}{y}\right)-\frac{5x}{y^{2}}\frac{5y}{y^{2}}\sin\!\left(\frac{5x}{y}\right)\right)\)
\(-\left(\frac{5x}{y^{2}}\frac{5x}{y^{2}}\sin\!\left(\frac{5x}{y}\right)-\frac{5x\cdot 2y}{\left(y^{2}\right)^{2}}\cos\!\left(\frac{5x}{y}\right)\right)\)
Given \(F(r,s,t)=r\!\left(9s^{4}-t^{5}\right)\text{,}\) compute:
\(F_{rst}=\)
\(0\)
Calculate all four second-order partial derivatives and check that \(f_{xy}=f_{yx}\text{.}\) Assume the variables are restricted to a domain on which the function is defined.
\(f_{xx} =\)
\(f_{yy} =\)
\(f_{xy} =\)
\(f_{yx} =\)
\(4y^{2}e^{2xy}\)
\(4x^{2}e^{2xy}\)
\(2e^{2xy}+4xye^{2xy}\)
\(2e^{2xy}+4xye^{2xy}\)
Calculate all four second-order partial derivatives of \(\displaystyle f(x,y) = \left(2x+4y\right)e^{y}\text{.}\)
\(f_{xx} \, (x,y) =\)
\(f_{xy} \, (x,y) =\)
\(f_{yx} \, (x,y) =\)
\(f_{yy} \, (x,y) =\)
\(0\)
\(2e^{y}\)
\(2e^{y}\)
\(4e^{y}+4e^{y}+\left(2x+4y\right)e^{y}\)
Let \(f(x,y) = \left(-\left(2x+y\right)\right)^{6}\text{.}\) Then
| \(\frac{\partial^2\!f}{\partial x\partial y}\) | \(=\) | |
| \(\frac{\partial^3\!f}{\partial x\partial y\partial x}\) | \(=\) | |
| \(\frac{\partial^3\!f}{\partial x^2\partial y}\) | \(=\) |
\(60\!\left(-\left(2x+y\right)\right)^{4}\)
\(-480\!\left(-\left(2x+y\right)\right)^{3}\)
\(-480\!\left(-\left(2x+y\right)\right)^{3}\)
If \(z_{xy} = 5 y\) and all of the second order partial derivatives of \(z\) are continuous, then
(a) \(z_{yx} =\)
(b) \(z_{xyx} =\)
(c) \(z_{xyy} =\)
\(5y\)
\(0\)
\(5\)
If \(z = f(x) + y g(x)\text{,}\) what can we say about \(z_{yy}\text{?}\)
- \(\displaystyle z_{yy} = 0\)
- \(\displaystyle z_{yy} = y\)
- \(\displaystyle z_{yy} = z_{xx}\)
- \(\displaystyle z_{yy} = g(x)\)
- We cannot say anything
Shown in Figure 10.3.9 is a contour plot of a function \(f\) with the values of \(f\) labeled on the contours. The point \((2,1)\) is highlighted in red.

a. Estimate the partial derivatives \(f_x(2,1)\) and \(f_y(2,1)\text{.}\)
b. Determine whether the second-order partial derivative \(f_{xx}(2,1)\) is positive or negative, and explain your thinking.
c. Determine whether the second-order partial derivative \(f_{yy}(2,1)\) is positive or negative, and explain your thinking.
d. Determine whether the second-order partial derivative \(f_{xy}(2,1)\) is positive or negative, and explain your thinking.
e. Determine whether the second-order partial derivative \(f_{yx}(2,1)\) is positive or negative, and explain your thinking.
f. Consider a function \(g\) of the variables \(x\) and \(y\) for which \(g_x(2,2) > 0\) and \(g_{xx}(2,2) \lt 0\text{.}\) Sketch possible behavior of some contours around \((2,2)\) on the left axes in Figure 10.3.10.


g. Consider a function \(h\) of the variables \(x\) and \(y\) for which \(h_x(2,2) > 0\) and \(h_{xy}(2,2) \lt 0\text{.}\) Sketch possible behavior of some contour lines around \((2,2)\) on the right axes in Figure 10.3.10.
The Heat Index, \(I\text{,}\) (measured in apparent degrees F) is a function of the actual temperature \(T\) outside (in degrees F) and the relative humidity \(H\) (measured as a percentage). A portion of the table which gives values for this function, \(I(T,H)\text{,}\) is reproduced in Table 10.3.11.
Table 10.3.11. Heat index.
| T \(\downarrow \backslash\) H \(\rightarrow\) | 70 | 75 | 80 | 85 |
| 90 | 106 | 109 | 112 | 115 |
| 92 | 112 | 115 | 119 | 123 |
| 94 | 118 | 122 | 127 | 132 |
| 96 | 125 | 130 | 135 | 141 |
- State the limit definition of the value \(I_{TT}(94,75)\text{.}\) Then, estimate \(I_{TT}(94,75)\text{,}\) and write one complete sentence that carefully explains the meaning of this value, including units.
- State the limit definition of the value \(I_{HH}(94,75)\text{.}\) Then, estimate \(I_{HH}(94,75)\text{,}\) and write one complete sentence that carefully explains the meaning of this value, including units.
- Finally, do likewise to estimate \(I_{HT}(94,75)\text{,}\) and write a sentence to explain the meaning of the value you found.
The temperature on a heated metal plate positioned in the first quadrant of the \(xy\)-plane is given by
Assume that temperature is measured in degrees Celsius and that \(x\) and \(y\) are each measured in inches.
- Determine \(C_{xx}(x,y)\) and \(C_{yy}(x,y)\text{.}\) Do not do any additional work to algebraically simplify your results.
- Calculate \(C_{xx}(1.1, 1.2)\text{.}\) Suppose that an ant is walking past the point \((1.1, 1.2)\) along the line \(y = 1.2\text{.}\) Write a sentence to explain the meaning of the value of \(C_{xx}(1.1, 1.2)\text{,}\) including units.
- Calculate \(C_{yy}(1.1, 1.2)\text{.}\) Suppose instead that an ant is walking past the point \((1.1, 1.2)\) along the line \(x = 1.1\text{.}\) Write a sentence to explain the meaning of the value of \(C_{yy}(1.1, 1.2)\text{,}\) including units.
- Determine \(C_{xy}(x,y)\) and hence compute \(C_{xy}(1.1, 1.2)\text{.}\) What is the meaning of this value? Explain, in terms of an ant walking on the heated metal plate.
Let \(f(x,y) = 8 - x^2 - y^2\) and \(g(x,y) = 8 - x^2 + 4xy - y^2\text{.}\)
- Determine \(f_x\text{,}\) \(f_y\text{,}\) \(f_{xx}\text{,}\) \(f_{yy}\text{,}\) \(f_{xy}\text{,}\) and \(f_{yx}\text{.}\)
- Evaluate each of the partial derivatives in (a) at the point \((0,0)\text{.}\)
- What do the values in (b) suggest about the behavior of \(f\) near \((0,0)\text{?}\) Plot a graph of \(f\) and compare what you see visually to what the values suggest.
- Determine \(g_x\text{,}\) \(g_y\text{,}\) \(g_{xx}\text{,}\) \(g_{yy}\text{,}\) \(g_{xy}\text{,}\) and \(g_{yx}\text{.}\)
- Evaluate each of the partial derivatives in (d) at the point \((0,0)\text{.}\)
- What do the values in (e) suggest about the behavior of \(g\) near \((0,0)\text{?}\) Plot a graph of \(g\) and compare what you see visually to what the values suggest.
- What do the functions \(f\) and \(g\) have in common at \((0,0)\text{?}\) What is different? What do your observations tell you regarding the importance of a certain second-order partial derivative?
Let \(f(x,y) = \frac{1}{2}xy^2\) represent the kinetic energy in Joules of an object of mass \(x\) in kilograms with velocity \(y\) in meters per second. Let \((a,b)\) be the point \((4,5)\) in the domain of \(f\text{.}\)
- Calculate \(\frac{ \partial^2 f}{\partial x^2}\) at the point \((a,b)\text{.}\) Then explain as best you can what this second order partial derivative tells us about kinetic energy.
- Calculate \(\frac{ \partial^2 f}{\partial y^2}\) at the point \((a,b)\text{.}\) Then explain as best you can what this second order partial derivative tells us about kinetic energy.
- Calculate \(\frac{ \partial^2 f}{\partial y \partial x}\) at the point \((a,b)\text{.}\) Then explain as best you can what this second order partial derivative tells us about kinetic energy.
- Calculate \(\frac{ \partial^2 f}{\partial x \partial y}\) at the point \((a,b)\text{.}\) Then explain as best you can what this second order partial derivative tells us about kinetic energy.
10.4: Linearization- Tangent Planes and Differentials
Exercises 10.4.5 Exercises
Find the linearization \(L \left( x, y \right)\) of the function \(f\left( x, y \right) = \sqrt{ 161 - 9 x^{2} - 4 y^{2} }\) at \(\left( -4, -2 \right)\text{.}\)
\(L \left( x, y \right) =\)
Note: Your answer should be an expression in x and y; e.g. “3x - 5y + 9”
\(36\!\left(x-\left(-4\right)\right)+8\!\left(y-\left(-2\right)\right)+1\)
Find the equation of the tangent plane to the surface \(z = e^{2 x/17} \ln \left( 1 y \right)\) at the point \((3,2, 0.9865)\text{.}\)
z =
Note: Your answer should be an expression of x and y; e.g. “5x + 2y - 3”
\(0.116061x+0.711624y+\left(-0.784911\right)\)
A student was asked to find the equation of the tangent plane to the surface \(z = x^{4}-y^{5}\) at the point \((x,y) = (4,5)\text{.}\) The student's answer was \(z = -2869 + 4x^{3} (x - 4) - \left(5y^{4}\right) (y - 5).\)
(a) At a glance, how do you know this is wrong. What mistakes did the student make? Select all that apply.
- The answer is not a linear function.
- The (x - 4) and (y - 5) should be x and y.
- The partial derivatives were not evaluated a the point.
- The -2869 should not be in the answer.
- All of the above
(b) Find the correct equation for the tangent plane.
\(z =\)
AC
(a) Check the local linearity of \(f(x,y) = e^{-x}\cos\!\left(y\right)\) near \(x=1,\ y=1.5\) by filling in the following table of values of \(f\) for \(x=0.9,\ 1,\ 1.1\) and \(y=1.4,\ 1.5,\ 1.6\text{.}\) Express values of \(f\) with 4 digits after the decimal point.
| \(x =\) | 0.9 | 1 | 1.1 |
| \(y = 1.4\) | |||
| \(y = 1.5\) | |||
| \(y = 1.6\) |
(b) Next, fill in the table for the values \(x=0.99,\ 1,\ 1.01\) and \(y = 1.49,\ 1.5,\ 1.51,\) again showing 4 digits after the decimal point.
| \(x =\) | 0.99 | 1 | 1.01 |
| \(y = 1.49\) | |||
| \(y = 1.5\) | |||
| \(y = 1.51\) |
Notice if the two tables look nearly linear, and whether the second looks more linear than the first (in particular, think about how you would decide if they were linear, or if the one were more closely linear than the other).
(c) Give the local linearization of \(f(x,y) = e^{-x}\cos\!\left(y\right)\) at \((1,1.5)\text{:}\)
Using the second of your tables:
\(f(x,y) \approx\)
Using the fact that \(f_x(x,y) = -e^{-x}\cos\!\left(y\right)\) and \(f_y(x,y) = -e^{-x}\sin\!\left(y\right)\text{:}\)
\(f(x,y) \approx\)
\(0.0691\)
\(0.0625\)
\(0.0566\)
\(0.0288\)
\(0.026\)
\(0.0235\)
\(-0.0119\)
\(-0.0107\)
\(-0.0097\)
\(0.03\)
\(0.0297\)
\(0.0294\)
\(0.0263\)
\(0.026\)
\(0.0258\)
\(0.0226\)
\(0.0224\)
\(0.0221\)
\(0.026+\frac{\left(0.0258-0.0263\right)\!\left(x-1\right)}{0.02}+\frac{\left(0.0224-0.0297\right)\!\left(y-1.5\right)}{0.02}\)
\(0.0260228+-0.0260228\!\left(x-1\right)+-0.366958\!\left(y-1.5\right)\)
Suppose that \(z\) is a linear function of \(x\) and \(y\) with slope -5 in the \(x\) direction and slope 5 in the \(y\) direction.
(a) A change of \(0.2\) in \(x\) and \(0.5\) in \(y\) produces what change in \(z\text{?}\)
change in \(z =\)
(b) If \(z=6\) when \(x=3\) and \(y=2\text{,}\) what is the value of \(z\) when \(x=2.7\) and \(y=1.9\text{?}\)
\(z =\)
\(-5\cdot 0.2+5\cdot 0.5\)
\(6+-5\cdot \left(2.7-3\right)+5\cdot \left(1.9-2\right)\)
Find the differential of the function \(w = x^{3} \sin(y^{5} z^{1})\)
\(dw =\)\(dx +\) \(dy +\) \(dz\)
\(3x^{2}\sin\!\left(y^{5}z^{1}\right)\)
\(5x^{3}y^{4}z^{1}\cos\!\left(y^{5}z^{1}\right)\)
\(1x^{3}y^{5}z^{0}\cos\!\left(y^{5}z^{1}\right)\)
The dimensions of a closed rectangular box are measured as 60 centimeters, 60 centimeters, and 80 centimeters, respectively, with the error in each measurement at most .2 centimeters. Use differentials to estimate the maximum error in calculating the surface area of the box.
square centimeters
\(160\)
One mole of ammonia gas is contained in a vessel which is capable of changing its volume (a compartment sealed by a piston, for example). The total energy \(U\) (in Joules) of the ammonia is a function of the volume \(V\) (in cubic meters) of the container, and the temperature \(T\) (in degrees Kelvin) of the gas. The differential \(dU\) is given by \(dU = 840 dV + 27.32 dT\text{.}\)
(a) How does the energy change if the volume is held constant and the temperature is decreased slightly?
- it increases slightly
- it does not change
- it decreases slightly
(b) How does the energy change if the temperature is held constant and the volume is increased slightly?
- it does not change
- it increases slightly
- it decreases slightly
(c) Find the approximate change in energy if the gas is compressed by 150 cubic centimeters and heated by 3 degrees Kelvin.
Change in energy = . Please include units in your answer.
C
An unevenly heated metal plate has temperature \(T(x,y)\) in degrees Celsius at a point \((x,y)\text{.}\) If \(T(2,1) = 119\text{,}\) \(T_x \, (2,1) = 19\text{,}\) and \(T_y \, (2,1) = -14\text{,}\) estimate the temperature at the point \((2.04,0.96)\text{.}\)
\(T(2.04,0.96) \approx\). Please include units in your answer.
\(120.32\ {\rm degC}\)
Let \(f\) be the function defined by \(f(x,y) = 2x^2+3y^3\text{.}\)
- Find the equation of the tangent plane to \(f\) at the point \((1,2)\text{.}\)
- Use the linearization to approximate the values of \(f\) at the points \((1.1, 2.05)\) and \((1.3,2.2)\text{.}\)
- Compare the approximations form part (b) to the exact values of \(f(1.1, 2.05)\) and \(f(1.3, 2.2)\text{.}\) Which approximation is more accurate. Explain why this should be expected.
Let \(f\) be the function defined by \(f(x,y) = x^{1/3}y^{1/3}\text{,}\) whose graph is shown in Figure 10.4.12.

- Determine
\[ \lim_{h \to 0} \frac{f(0+h,0)-f(0,0)}{h}. \nonumber \]
What does this limit tell us about \(f_x(0,0)\text{?}\)
- Note that \(f(x,y)=f(y,x)\text{,}\) and this symmetry implies that \(f_x(0,0) = f_y(0,0)\text{.}\) So both partial derivatives of \(f\) exist at \((0,0)\text{.}\) A picture of the surface defined by \(f\) near \((0,0)\) is shown in Figure 10.4.12. Based on this picture, do you think \(f\) is locally linear at \((0,0)\text{?}\) Why?
- Show that the curve where \(x=y\) on the surface defined by \(f\) is not differentiable at 0. What does this tell us about the local linearity of \(f\) at \((0,0)\text{?}\)
- Is the function \(f\) defined by \(f(x,y) = \frac{x^2}{y^2+1}\) locally linear at \((0,0)\text{?}\) Why or why not?
Let \(g\) be a function that is differentiable at \((-2,5)\) and suppose that its tangent plane at this point is given by \(z = -7 + 4(x+2) - 3(y-5)\text{.}\)
- Determine the values of \(g(-2,5)\text{,}\) \(g_x(-2,5)\text{,}\) and \(g_y(-2,5)\text{.}\) Write one sentence to explain your thinking.
- Estimate the value of \(g(-1.8, 4.7)\text{.}\) Clearly show your work and thinking.
- Given changes of \(dx = -0.34\) and \(dy = 0.21\text{,}\) estimate the corresponding change in \(g\) that is given by its differential, \(dg\text{.}\)
- Suppose that another function \(h\) is also differentiable at \((-2,5)\text{,}\) but that its tangent plane at \((-2,5)\) is given by \(3x + 2y - 4z = 9.\) Determine the values of \(h(-2,5)\text{,}\) \(h_x(-2,5)\text{,}\) and \(h_y(-2,5)\text{,}\) and then estimate the value of \(h(-1.8, 4.7)\text{.}\) Clearly show your work and thinking.
In the following questions, we determine and apply the linearization for several different functions.
- Find the linearization \(L(x,y)\) for the function \(f\) defined by \(f(x,y) = \cos(x)(2e^{2y}+e^{-2y})\) at the point \((x_0,y_0) = (0,0)\text{.}\) Use the linearization to estimate the value of \(f(0.1, 0.2)\text{.}\) Compare your estimate to the actual value of \(f(0.1, 0.2)\text{.}\)
- The Heat Index, \(I\text{,}\) (measured in apparent degrees F) is a function of the actual temperature \(T\) outside (in degrees F) and the relative humidity \(H\) (measured as a percentage). A portion of the table which gives values for this function, \(I=I(T,H)\text{,}\) is provided in Table 10.4.13.
Table 10.4.13. Heat index.
Suppose you are given that \(I_T(94,75) = 3.75\) and \(I_H(94,75) = 0.9\text{.}\) Use this given information and one other value from the table to estimate the value of \(I(93.1,77)\) using the linearization at \((94,75)\text{.}\) Using proper terminology and notation, explain your work and thinking.T \(\downarrow \backslash\) H \(\rightarrow\) \(70\) \(75\) \(80\) \(85\) \(90\) \(106\) \(109\) \(112\) \(115\) \(92\) \(112\) \(115\) \(119\) \(123\) \(94\) \(118\) \(122\) \(127\) \(132\) \(96\) \(125\) \(130\) \(135\) \(141\) - Just as we can find a local linearization for a differentiable function of two variables, we can do so for functions of three or more variables. By extending the concept of the local linearization from two to three variables, find the linearization of the function \(h(x,y,z) = e^{2x}(y+z^2)\) at the point \((x_0,y_0,z_0) = (0, 1, -2)\text{.}\) Then, use the linearization to estimate the value of \(h(-0.1, 0.9, -1.8)\text{.}\)
In the following questions, we investigate two different applied settings using the differential.
- Let \(f\) represent the vertical displacement in centimeters from the rest position of a string (like a guitar string) as a function of the distance \(x\) in centimeters from the fixed left end of the string and \(y\) the time in seconds after the string has been plucked. (An interesting video of this can be seen at
https://www.youtube.com/watch?v=TKF6nFzpHBUA.) A simple model for \(f\) could be\[ f(x,y) = \cos(x)\sin(2y). \nonumber \]Use the differential to approximate how much more this vibrating string is vertically displaced from its position at \((a,b) = \left(\frac{\pi}{4}, \frac{\pi}{3} \right)\) if we decrease \(a\) by \(0.01\) cm and increase the time by \(0.1\) seconds. Compare to the value of \(f\) at the point \(\left(\frac{\pi}{4}-0.01, \frac{\pi}{3}+0.1\right)\text{.}\)
- Resistors used in electrical circuits have colored bands painted on them to indicate the amount of resistance and the possible error in the resistance. When three resistors, whose resistances are \(R_1\text{,}\) \(R_2\text{,}\) and \(R_3\text{,}\) are connected in parallel, the total resistance \(R\) is given by
\[ \frac1R = \frac1{R_1} + \frac1{R_2} + \frac1{R_3}. \nonumber \]
Suppose that the resistances are \(R_1=25\Omega\text{,}\) \(R_2=40\Omega\text{,}\) and \(R_3=50\Omega\text{.}\) Find the total resistance \(R\text{.}\) If you know each of \(R_1\text{,}\) \(R_2\text{,}\) and \(R_3\) with a possible error of \(0.5\)%, estimate the maximum error in your calculation of \(R\text{.}\)
In this section we argued that if \(f = f(x,y)\) is a function of two variables and if \(f_x\) and \(f_y\) both exist and are continuous in an open disk containing the point \((x_0,y_0)\text{,}\) then \(f\) is differentiable at \((x_0,y_0)\text{.}\) This condition ensures that \(f\) is differentiable at \((x_0,y_0)\text{,}\) but it does not define what it means for \(f\) to be differentiable at \((x_0,y_0)\text{.}\) In this exercise we explore the definition of differentiability of a function of two variables in more detail. Throughout, let \(g\) be the function defined by \(g(x,y)= \sqrt{|xy|}\text{.}\)
- Use appropriate technology to plot the graph of \(g\) on the domain \([-1,1] \times [-1,1]\text{.}\) Explain why \(g\) is not locally linear at \((0,0)\text{.}\)
- Show that both \(g_x(0,0)\) and \(g_y(0,0)\) exist. If \(g\) is locally linear at \((0,0)\text{,}\) what must be the equation of the tangent plane \(L\) to \(g\) at \((0,0)\text{?}\)
- Recall that if a function \(f = f(x)\) of a single variable is differentiable at \(x=x_0\text{,}\) then
\[ f'(x_0) = \lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h} \nonumber \]
exists. We saw in single variable calculus that the existence of \(f'(x_0)\) means that the graph of \(f\) is locally linear at \(x=x_0\text{.}\) In other words, the graph of \(f\) looks like its linearization \(L(x) = f(x_0)+f'(x_0)(x-x_0)\) for \(x\) close to \(x_0\text{.}\) That is, the values of \(f(x)\) can be closely approximated by \(L(x)\) as long as \(x\) is close to \(x_0\text{.}\) We can measure how good the approximation of \(L(x)\) is to \(f(x)\) with the error function
\[ E(x) = L(x) - f(x) = f(x_0)+f'(x_0)(x-x_0) - f(x). \nonumber \]As \(x\) approaches \(x_0\text{,}\) \(E(x)\) approaches \(f(x_0)+f'(x_0)(0) - f(x_0) = 0\text{,}\) and so \(L(x)\) provides increasingly better approximations to \(f(x)\) as \(x\) gets closer to \(x_0\text{.}\) Show that, even though \(g(x,y) = \sqrt{|xy|}\) is not locally linear at \((0,0)\text{,}\) its error term
\[ E(x,y) = L(x,y) - g(x,y) \nonumber \]at \((0,0)\) has a limit of \(0\) as \((x,y)\) approaches \((0,0)\text{.}\) (Use the linearization you found in part (b).) This shows that just because an error term goes to \(0\) as \((x,y)\) approaches \((x_0,y_0)\text{,}\) we cannot conclude that a function is locally linear at \((x_0,y_0)\text{.}\)
- As the previous part illustrates, having the error term go to \(0\) does not ensure that a function of two variables is locally linear. Instead, we need a notation of a relative error. To see how this works, let us return to the single variable case for a moment and consider \(f = f(x)\) as a function of one variable. If we let \(x = x_0+h\text{,}\) where \(|h|\) is the distance from \(x\) to \(x_0\text{,}\) then the relative error in approximating \(f(x_0+h)\) with \(L(x_0+h)\) is
\[ \frac{E(x_0+h)}{h}. \nonumber \]
Show that, for a function \(f = f(x)\) of a single variable, the limit of the relative error is \(0\) as \(h\) approaches \(0\text{.}\)
- Even though the error term for a function of two variables might have a limit of \(0\) at a point, our example shows that the function may not be locally linear at that point. So we use the concept of relative error to define differentiability of a function of two variables. When we consider differentiability of a function \(f = f(x,y)\) at a point \((x_0,y_0)\text{,}\) then if \(x = x_0+h\) and \(y = y_0+k\text{,}\) the distance from \((x,y)\) to \((x_0,y_0)\) is \(\sqrt{h^2+k^2}\text{.}\)
A function \(f = f(x,y)\) is differentiable at a point \((x_0,y_0)\) if there is a linear function \(L = L(x,y) = f(x_0,y_0) + m(x-x_0) + n(y-y_0)\) such that the relative error
\[ \frac{E(x_0+h,y_0+k)}{\sqrt{h^2+k^2}}, \nonumber \]has at limit of \(0\) at \((h,k) = (0,0)\text{,}\) where \(E(x,y) = f(x,y) - L(x,y)\text{,}\) \(h=x-x_0\text{,}\) and \(k = y-y_0\text{.}\)
A function \(f\) is differentiable if it is differentiable at every point in its domain. The function \(L\) in the definition is the linearization of \(f\) at \((x_0,y_0)\text{.}\) Verify that \(g(x,y) = \sqrt{|xy|}\) is not differentiable at \((0,0)\) by showing that the relative error at \((0,0)\) does not have a limit at \((0,0)\text{.}\) Conclude that the existence of partial derivatives at a point is not enough to ensure differentiability at that point. (Hint: Consider the limit along different paths.)
Suppose that a function \(f = f(x,y)\) is differentiable at a point \((x_0,y_0)\text{.}\) Let \(L = L(x,y) = f(x_0,y_0) + m(x-x_0) + n(y-y_0)\) as in the conditions of Definition 10.4.14. Show that \(m = f_x(x_0,y_0)\) and \(n = f_y(x_0,y_0)\text{.}\) (Hint: Calculate the limits of the relative errors when \(h = 0\) and \(k = 0\text{.}\))
We know that if a function of a single variable is differentiable at a point, then that function is also continuous at that point. In this exercise we determine that the same property holds for functions of two variables. A function \(f\) of the two variables \(x\) and \(y\) is continuous at a point \((x_0,y_0)\) in its domain if
or (letting \(x=x_0+h\) and \(y = y_0 + k\text{,}\)
Show that if \(f\) is differentiable at \((x_0,y_0)\text{,}\) then \(f\) is continuous at \((x_0,y_0)\text{.}\) (Hint: Multiply both sides of the equality that comes from differentiability by \(\lim_{(h,k) \to (0,0)} \sqrt{h^2+k^2}\text{.}\))
10.5: The Chain Rule
Exercises 10.5.4 Exercises
Use the chain rule to find \(\frac{dz}{dt}\text{,}\) where
First the pieces:
\(\frac{\partial z}{\partial x} =\)
\(\frac{\partial z}{\partial y} =\)
\(\frac{dx}{dt} =\)
\(\frac{dy}{dt} =\)
End result (in terms of just \(t\)):
\(\frac{dz}{dt} =\)
\(2xy+y^{2}\)
\(x^{2}+2xy\)
\(-5t^{4}\)
\(-2t^{1}\)
\(\left(2\!\left(1+\left(-1\right)t^{5}\right)\!\left(3+\left(-1\right)t^{2}\right)+\left(3+\left(-1\right)t^{2}\right)^{2}\right)\!\left(-1\right)\cdot 5t^{4}+\left(2\!\left(1+\left(-1\right)t^{5}\right)\!\left(3+\left(-1\right)t^{2}\right)+\left(1+\left(-1\right)t^{5}\right)^{2}\right)\!\left(-1\right)\cdot 2t^{1}\)
Use the chain rule to find \(\frac{\partial z}{\partial s}\) and \(\frac{\partial z}{\partial t}\text{,}\) where
First the pieces:
\(\frac{\partial z}{\partial x} =\) \(\frac{\partial z}{\partial y} =\)
\(\frac{\partial x}{\partial s} =\) \(\frac{\partial x}{\partial t} =\)
\(\frac{\partial y}{\partial s} =\) \(\frac{\partial y}{\partial t} =\)
And putting it all together:
\(\frac{\partial z}{\partial s} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial s} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial s}\) and \(\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial t} + \frac{\partial z}{\partial y}\frac{\partial y}{\partial t}\)
\(y\tan\!\left(y\right)\exp\!\left(xy\right)\)
\(\exp\!\left(xy\right)\sec^{2}\!\left(y\right)+\tan\!\left(y\right)x\exp\!\left(xy\right)\)
\(4\)
\(5\)
\(\frac{3}{3t}\)
\(\frac{-3s}{3t^{2}}\)
Suppose \(\displaystyle w = \frac{x}{y} + \frac{y}{z}\text{,}\) where
\(x = e^{5t},\ y = 2 + \sin \left( 3t \right)\text{,}\) and \(z = 2 + \cos \left( 6t \right)\text{.}\)
A) Use the chain rule to find \(\frac{dw}{dt}\) as a function of x, y, z, and t. Do not rewrite x, y, and z in terms of t, and do not rewrite \(e^{5t}\) as x.
\(\frac{dw}{dt}\) =
Note: You may want to use exp() for the exponential function. Your answer should be an expression in x, y, z, and t; e.g. “3x - 4y”
B) Use part A to evaluate \(\frac{dw}{dt}\) when \(t = 0\text{.}\)
\(\frac{5\exp\!\left(5t\right)}{y}+\left(\frac{-x}{y^{2}}+\frac{1}{z}\right)\cdot 3\cos\!\left(3t\right)+\frac{-y}{z^{2}}\!\left(-6\right)\sin\!\left(6t\right)\)
\(2.75\)
If \(z = \left(x+y\right)e^{y}\) and \(x = u^{2}+v^{2}\) and \(y = u^{2}-v^{2}\text{,}\) find the following partial derivatives using the chain rule. Enter your answers as functions of \(u\) and \(v\text{.}\)
\(\displaystyle \frac{\partial z}{\partial u} =\)
\(\displaystyle \frac{\partial z}{\partial v} =\)
\(2\cdot 2ue^{u^{2}-v^{2}}+2u^{2}e^{u^{2}-v^{2}}\cdot 2u\)
\(-2u^{2}e^{u^{2}-v^{2}}\cdot 2v\)
If
find \(\partial z/\partial u\) and \(\partial z/\partial v\text{.}\) The variables are restricted to domains on which the functions are defined.
\(\partial z/\partial u =\)
\(\partial z/\partial v =\)
\(0\)
\(\cos\!\left(v^{2}\right)\cdot 2v\)
Let \(z=g(u,v)\) and \(u(r,s),v(r,s)\text{.}\) How many terms are there in the expression for \(\partial z/\partial r\text{?}\)
terms
\(2\)
Let \(W(s,t) = F(u(s,t), v(s,t))\) where
\(W_s(1,0) =\) \(W_t(1,0) =\)
\(-47\)
\(11\)
The radius of a right circular cone is increasing at a rate of 3 inches per second and its height is decreasing at a rate of 5 inches per second. At what rate is the volume of the cone changing when the radius is 40 inches and the height is 40 inches?
cubic inches per second
\(1675.51608191456\)
In a simple electric circuit, Ohm's law states that \(V = IR\text{,}\) where V is the voltage in volts, I is the current in amperes, and R is the resistance in ohms. Assume that, as the battery wears out, the voltage decreases at 0.03 volts per second and, as the resistor heats up, the resistance is increasing at 0.02 ohms per second. When the resistance is 100 ohms and the current is 0.02 amperes, at what rate is the current changing?
amperes per second
\(-0.000304\)
Suppose \(z = x^{2} \sin y\text{,}\) \(x = 2 s^{2} + 1 t^{2}\text{,}\) \(y = -6 s t\text{.}\)
A. Use the chain rule to find \(\frac{\partial z}{\partial s}\) and \(\frac{\partial z}{\partial t}\) as functions of x, y, s and t.
\(\frac{\partial z}{\partial s} =\)
\(\frac{\partial z}{\partial t} =\)
B. Find the numerical values of \(\frac{\partial z}{\partial s}\) and \(\frac{\partial z}{\partial t}\) when \(\left( s , t \right) = \left( -3 , 3 \right)\text{.}\)
\(\frac{\partial z}{\partial s} \left( -3 , 3 \right) =\)
\(\frac{\partial z}{\partial t} \left( -3 , 3 \right) =\)
\(8sx\sin\!\left(y\right)+-6tx^{2}\cos\!\left(y\right)\)
\(4tx\sin\!\left(y\right)+-6sx^{2}\cos\!\left(y\right)\)
\(11244.2989304861\)
\(-11063.2512786582\)
Find the indicated derivative. In each case, state the version of the Chain Rule that you are using.
- \(\frac{df}{dt}\text{,}\) if \(f(x,y) = 2x^2y\text{,}\) \(x=\cos(t)\text{,}\) and \(y=\ln(t)\text{.}\)
- \(\frac{\partial f}{\partial w}\text{,}\) if \(f(x,y) = 2x^2y\text{,}\) \(x=w+z^2\text{,}\) and \(y=\frac{2z+1}{w}\)
- \(\frac{\partial f}{\partial v}\text{,}\) if \(f(x,y,z) = 2x^2y+z^3\text{,}\) \(x=u-v+2w\text{,}\) \(y=w2^v-u^3\text{,}\) and \(z = u^2-v\)
Let \(z = u^2 - v^2\) and suppose that
- Find the values of \(u\) and \(v\) that correspond to \(x=0\) and \(y=2\pi/3\text{.}\)
- Use the Chain Rule to find the general partial derivatives
\[ \frac{\partial z}{\partial x} \ \mbox{and} \ \frac{\partial z}{\partial y} \nonumber \]
and then determine both \(\frac{\partial z}{\partial x}\bigm|_{(0, \frac{2\pi}{3})}\) and \(\frac{\partial z}{\partial y}\bigm|_{(0, \frac{2\pi}{3})}\text{.}\)
Suppose that \(T = x^2 + y^2 - 2z\) where
- Construct a tree diagram representing the dependencies among the variables.
- Apply the chain rule to find the partial derivatives
\[ \frac{\partial T}{\partial\rho}, \frac{\partial T}{\partial\phi}, \ \mbox{and} \ \frac{\partial T}{\partial\theta}. \ \nonumber \]
Suppose that the temperature on a metal plate is given by the function \(T\) with
where the temperature is measured in degrees Fahrenheit and \(x\) and \(y\) are each measured in feet. Now suppose that an ant is walking on the metal plate in such a way that it walks in a straight line from the point \((1,4)\) to the point \((5,6)\text{.}\)
- Find parametric equations \((x(t),y(t))\) for the ant's coordinates as it walks the line from \((1,4)\) to \((5,6)\text{.}\)
- What can you say about \(\frac{dx}{dt}\) and \(\frac{dy}{dt}\) for every value of \(t\text{?}\)
- Determine the instantaneous rate of change in temperature with respect to \(t\) that the ant is experiencing at the moment it is halfway from \((1,4)\) to \((5,6)\text{,}\) using your parametric equations for \(x\) and \(y\text{.}\) Include units on your answer.
There are several proposed formulas to approximate the surface area of the human body. One model 1 uses the formula
where \(A\) is the surface area in square meters, \(h\) is the height in centimeters, and \(w\) is the weight in kilograms.
Since a person's height \(h\) and weight \(w\) change over time, \(h\) and \(w\) are functions of time \(t\text{.}\) Let us think about what is happening to a child whose height is \(60\) centimeters and weight is \(9\) kilograms. Suppose, furthermore, that \(h\) is increasing at an instantaneous rate of 20 centimeters per year and \(w\) is increasing at an instantaneous rate of \(5\) kg per year.
Determine the instantaneous rate at which the child's surface area is changing at this point in time.
Let \(z = f(x,y) = 50 - (x+1)^2 - (y+3)^2\) and \(z = h(x,y) = 24 - 2x - 6y\text{.}\)
Suppose a person is walking on the surface \(z = f(x,y)\) in such a way that she walks the curve which is the intersection of \(f\) and \(h\text{.}\)
- Show that \(x(t) = 4 \cos(t)\) and \(y(t) = 4 \sin(t)\) is a parameterization of the “shadow” in the \(xy\)-plane of the curve that is the intersection of the graphs of \(f\) and \(h\text{.}\)
- Use the parameterization from part (a) to find the instantaneous rate at which her height is changing with respect to time at the instant \(t = 2\pi/3\text{.}\)
The voltage \(V\) (in volts) across a circuit is given by Ohm's Law: \(V = IR\text{,}\) where \(I\) is the current (in amps) in the circuit and \(R\) is the resistance (in ohms). Suppose we connect two resistors with resistances \(R_1\) and \(R_2\) in parallel as shown in Figure 10.5.5. The total resistance \(R\) in the circuit is then given by
\[ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}. \nonumber \]
- Assume that the current, \(I\text{,}\) and the resistances, \(R_1\) and \(R_2\text{,}\) are changing over time, \(t\text{.}\) Use the Chain Rule to write a formula for \(\frac{dV}{dt}\text{.}\)
- Suppose that, at some particular point in time, we measure the current to be 3 amps and that the current is increasing at \(\frac{1}{10}\) amps per second, while resistance \(R_1\) is 2 ohms and decreasing at the rate of 0.2 ohms per second and \(R_2\) is 1 ohm and increasing at the rate of \(0.5\) ohms per second. At what rate is the voltage changing at this point in time?
10.6: Directional Derivatives and the Gradient
Consider the function \(f(x,y,z) = xy + yz^2 + xz^3\text{.}\)
Find the gradient of \(f\text{:}\)
\(\langle\), , \(\rangle\)
Find the gradient of \(f\) at the point (2, 3, 5).
\(\langle\), , \(\rangle\)
Find the rate of change of the function \(f\) at the point (2, 3,5) in the direction \(\mathbf u = \langle 4/\sqrt{66}, -5/\sqrt{66}, -5/\sqrt{66} \rangle\text{.}\)
\(y+z^{3}\)
\(x+z^{2}\)
\(2yz+3xz^{2}\)
\(128\)
\(27\)
\(180\)
\(-64.376849782191\)
If \(f \left( x, y \right) = 3 x^{2} - 1 y^{2}\text{,}\) find the value of the directional derivative at the point \(\left( -1, -4 \right)\) in the direction given by the angle \(\theta = \frac{2 \pi}{6}\text{.}\)
\(3.92820323027551\)
Find the directional derivative of \(\displaystyle f(x,y,z) = 4xy+z^{2}\) at the point \((-5,3,-2)\) in the direction of the maximum rate of change of \(f\text{.}\)
\(f_{\lt B>\lt I>u\lt /B>\lt /I>} \, (-5,3,-2) = D_{\lt B>\lt I>u\lt /B>\lt /I>} \, f(-5,3,-2) =\)
\(23.6643\)
The temperature at any point in the plane is given by \(\displaystyle T(x,y) = \frac{100}{x^{2}+y^{2}+3}\text{.}\)
(a) What shape are the level curves of \(T\text{?}\)
- hyperbolas
- circles
- lines
- ellipses
- parabolas
- none of the above
(b) At what point on the plane is it hottest?
What is the maximum temperature?
(c) Find the direction of the greatest increase in temperature at the point \((-3,-3)\text{.}\)
What is the value of this maximum rate of change, that is, the maximum value of the directional derivative at \((-3,-3)\text{?}\)
(d) Find the direction of the greatest decrease in temperature at the point \((-3,-3)\text{.}\)
What is the value of this most negative rate of change, that is, the minimum value of the directional derivative at \((-3,-3)\text{?}\)
B
\(\left(0,0\right)\)
\(33.3333\)
\(\left<1.36054,1.36054\right>\)
\(1.9241\)
\(\left<-1.36054,-1.36054\right>\)
The temperature at a point (x,y,z) is given by \(\displaystyle T(x,y,z) = 200e^{-x^2 -y^2/4 - z^2/9}\text{,}\) where \(T\) is measured in degrees Celsius and x,y, and z in meters. There are lots of places to make silly errors in this problem; just try to keep track of what needs to be a unit vector.
Find the rate of change of the temperature at the point (-1, 1, 2) in the direction toward the point (-1, 3, -3).
In which direction (unit vector) does the temperature increase the fastest at (-1, 1, 2)?
\(\langle\), ,\(\rangle\)
What is the maximum rate of increase of \(T\) at (-1, 1, 2)?
\(8.33860305193074\)
\(0.948354065592898\)
\(-0.237088516398225\)
\(-0.210745347909533\)
\(77.4821403113886\)
If \(\displaystyle f(x,y,z) = 2zy^{2}\text{,}\) then the gradient at the point \((2,2,4)\) is
\(\nabla f (2,2,4) =\)
\(\left<0,32,8\right>\)
The concentration of salt in a fluid at \((x,y,z)\) is given by \(F(x,y,z) = 2x^{2}+3y^{4}+2x^{2}z^{2}\) mg/cm\({}^3\text{.}\) You are at the point \((-1,1,-1)\text{.}\)
(a) In which direction should you move if you want the concentration to increase the fastest?
direction:
(Give your answer as a vector.)
(b) You start to move in the direction you found in part (a) at a speed of \(5\) cm/sec. How fast is the concentration changing?
rate of change =
\(-8\,\mathit{\vec i}+12\,\mathit{\vec j}-4\,\mathit{\vec k}\)
\(5\sqrt{-8\cdot \left(-8\right)+12\cdot 12+-4\cdot \left(-4\right)}\)
At a certain point on a heated metal plate, the greatest rate of temperature increase, 4 degrees Celsius per meter, is toward the northeast. If an object at this point moves directly north, at what rate is the temperature increasing?
degrees Celsius per meter
\(\frac{4}{\sqrt{2}}\)
Suppose that you are climbing a hill whose shape is given by \(z = 902 - 0.07 x^2 -0.1 y^2\text{,}\) and that you are at the point (40, 70, 300).
In which direction (unit vector) should you proceed initially in order to reach the top of the hill fastest?
\(\langle\),\(\rangle\)
If you climb in that direction, at what angle above the horizontal will you be climbing initially (radian measure)?
\(-0.371390676354104\)
\(-0.928476690885259\)
\(1.5045735390203\)
Are the following statements true or false?
- The gradient vector \(\nabla f(a,b)\) is tangent to the contour of \(f\) at \((a,b)\text{.}\)
- \(f_{\vec{u}} \, (a,b) = || \nabla f(a,b) ||\text{.}\)
- \(f_{\vec{u}} \, (a,b)\) is parallel to \(\vec{u}\text{.}\)
- If \(\vec{u}\) is perpendicular to \(\nabla f(a,b)\text{,}\) then \(f_{\vec{u}} \, (a,b) = \langle 0, 0 \rangle\text{.}\)
- If \(\vec{u}\) is a unit vector, then \(f_{\vec{u}} (a,b)\) is a vector.
- Suppose \(f_x(a,b)\) and \(f_y(a,b)\) both exist. Then there is always a direction in which the rate of change of \(f\) at \((a,b)\) is zero.
- If \(f(x,y)\) has \(f_x(a,b) = 0\) and \(f_y(a,b) = 0\) at the point \((a,b)\text{,}\) then \(f\) is constant everywhere.
- \(\nabla f(a,b)\) is a vector in 3-dimensional space.
Let \(E(x,y) = \frac{100}{1+(x-5)^2 + 4(y-2.5)^2}\) represent the elevation on a land mass at location \((x,y)\text{.}\) Suppose that \(E\text{,}\) \(x\text{,}\) and \(y\) are all measured in meters.
- Find \(E_x(x,y)\) and \(E_y(x,y)\text{.}\)
- Let \(\mathbf{u}\) be a unit vector in the direction of \(\langle -4,3 \rangle\text{.}\) Determine \(D_{\mathbf{u}} E(3,4)\text{.}\) What is the practical meaning of \(D_{\mathbf{u}} E(3,4)\) and what are its units?
- Find the direction of greatest increase in \(E\) at the point \((3,4)\text{.}\)
- Find the instantaneous rate of change of \(E\) in the direction of greatest decrease at the point \((3,4)\text{.}\) Include units on your answer.
- At the point \((3,4)\text{,}\) find a direction \(\mathbf{w}\) in which the instantaneous rate of change of \(E\) is 0.
Find all directions in which the directional derivative of \(f(x,y) = ye^{-xy}\) is 1 at the point \((0,2)\text{.}\)
Find, if possible, a function \(f\) such that
If not possible, explain why.
Let \(f(x,y) = x^2+3y^2\text{.}\)
a. Find \(\nabla f(x,y)\) and \(\nabla f(1,2)\text{.}\)
b. Find the direction of greatest increase in \(f\) at the point \((1,2)\text{.}\) Explain. A graph of the surface defined by \(f\) is shown at left in Figure 10.6.7. Illustrate this direction on the surface.
c. A contour diagram of \(f\) is shown at right in Figure 10.6.7. Illustrate your calculation from (b) on this contour diagram.


d. Find a direction \(\mathbf{w}\) for which the derivative of \(f\) in the direction of \(\mathbf{w}\) is zero.
The properties of the gradient that we have observed for functions of two variables also hold for functions of more variables. In this problem, we consider a situation where there are three independent variables. Suppose that the temperature in a region of space is described by
and that you are standing at the point \((1,2,-1)\text{.}\)
- Find the instantaneous rate of change of the temperature in the direction of \(\mathbf{v}=\langle 0, 1, 2\rangle\) at the point \((1,2,-1)\text{.}\) Remember that you should first find a unit vector in the direction of \(\mathbf{v}\text{.}\)
- In what direction from the point \((1,2,-1)\) would you move to cause the temperature to decrease as quickly as possible?
- How fast does the temperature decrease in this direction?
- Find a direction in which the temperature does not change at \((1,2,-1)\text{.}\)
Figure 10.6.8 shows a plot of the gradient \(\nabla f\) at several points for some function \(f=f(x,y)\text{.}\)

- Consider each of the three indicated points, and draw, as best as you can, the contour through that point.
- Beginning at each point, draw a curve on which \(f\) is continually decreasing.
10.7: Optimization
The function
has a critical point at \((0,0)\text{.}\)
What is the value of \(D\) at this critical point? \(D =\)
What type of critical point is it?
- maximum
- minimum
- saddle point
- point with unknown behavior
\(2\cdot 25\)
\(\text{maximum}\)
Consider the function
Find and classify all critical points of the function. If there are more blanks than critical points, leave the remaining entries blank.
\(f_x =\)
\(f_y =\)
\(f_{xx} =\)
\(f_{xy} =\)
\(f_{yy} =\)
There are several critical points to be listed. List them lexicograhically, that is in ascending order by x-coordinates, and for equal x-coordinates in ascending order by y-coordinates (e.g., (1,1), (2, -1), (2, 3) is a correct order)
The critical point with the smallest x-coordinate is
(, ) Classification: (local minimum, local maximum, saddle point, cannot be determined)
The critical point with the next smallest x-coordinate is
(, ) Classification: (local minimum, local maximum, saddle point, cannot be determined)
The critical point with the next smallest x-coordinate is
(, ) Classification: (local minimum, local maximum, saddle point, cannot be determined)
The critical point with the next smallest x-coordinate is
(, ) Classification: (local minimum, local maximum, saddle point, cannot be determined)
The critical point with the next smallest x-coordinate is
(, ) Classification: (local minimum, local maximum, saddle point, cannot be determined)
\(\left(18-2x\right)\!\left(18y-y^{2}\right)\)
\(\left(18x-x^{2}\right)\!\left(18-2y\right)\)
\(-2\!\left(18y-y^{2}\right)\)
\(\left(18-2x\right)\!\left(18-2y\right)\)
\(-2\!\left(18x-x^{2}\right)\)
\(0\)
\(0\)
saddle point
\(0\)
\(18\)
saddle point
\(9\)
\(9\)
local maximum
\(18\)
\(0\)
saddle point
\(18\)
\(18\)
saddle point
Suppose \(f(x, y) = xy - ax - by\text{.}\)
(A) How many local minimum points does \(f\) have in \(\mathbf{R}^{2}\text{?}\) (The answer is an integer).
(B) How many local maximum points does \(f\) have in \(\mathbf{R}^{2}\text{?}\)
(C) How many saddle points does \(f\) have in \(\mathbf{R}^{2}\text{?}\)
\(0\)
\(0\)
\(1\)
Let \(f(x,y) = 1/x + 2/y + 3 x + 4 y\) in the region \(R\) where \(x, y > 0\text{.}\)
Explain why \(f\) must have a global minimum at some point in \(R\) (note that \(R\) is unbounded---how does this influence your explanation?). Then find the global minimum.
minimum =
\(2\sqrt{3\cdot 1}+2\sqrt{4\cdot 2}\)
Each of the following functions has at most one critical point. Graph a few level curves and a few gradients and, on this basis alone, decide whether the critical point is a local maximum, a local minimum, a saddle point, or that there is no critical point.
For \(f(x, y) = e^{-2 x^2 - 4 y^2}\text{,}\) type of critical point:
- Local Maximum
- Local Minimum
- Saddle Point
- No Critical Point
For \(f(x, y) = e^{2 x^2 - 4 y^2}\text{,}\) type of critical point:
- Local Maximum
- Local Minimum
- Saddle Point
- No Critical Point
For \(f(x, y) = 2 x^2+ 4 y^2+ 4\text{,}\) type of critical point:
- Local Maximum
- Local Minimum
- Saddle Point
- No Critical Point
For \(f(x, y) = 2 x^2+ 4 y+ 4\text{,}\) type of critical point:
- Local Maximum
- Local Minimum
- Saddle Point
- No Critical Point
Find the absolute minimum and absolute maximum of
on the closed triangular region with vertices \((0,0), (8, 0)\) and \((8, 12)\text{.}\)
List the minimum/maximum values as well as the point(s) at which they occur. If a min or max occurs at multiple points separate the points with commas.
Minimum value:
Occurs at
Maximum value:
Occurs at
\(-39\)
\(\left(8,0\right)\)
\(57\)
\(\left(8,12\right)\)
Find the maximum and minimum values of \(f(x, y) = xy\) on the ellipse \(5\!x^{2} + y^{2} = 3\text{.}\)
maximum value =
minimum value =
\(0.670820393249937\)
\(-0.670820393249937\)
Find \(A\) and \(B\) so that \(f(x,y) = x^2 + Ax + y^2 + B\) has a local minimum at the point \((7, 0)\text{,}\) with \(z\)-coordinate 5.
\(A =\)
\(B =\)
\(-14\)
\(5+7\cdot 7\)
The contours of a function \(f\) are shown in the figure below.
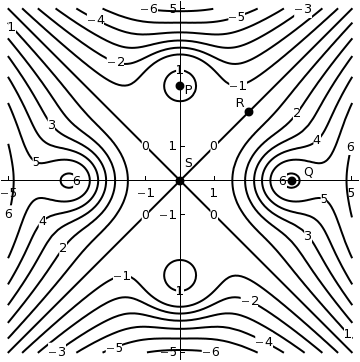

For each of the points shown, indicate whether you think it is a local maximum, local minimum, saddle point, or none of these.
(a) Point P is
- a local maximum
- a local minimum
- a saddle point
- none of these
(b) Point Q is
- a local maximum
- a local minimum
- a saddle point
- none of these
(c) Point R is
- a local maximum
- a local minimum
- a saddle point
- none of these
(d) Point S is
- a local maximum
- a local minimum
- a saddle point
- none of these
\(\text{a local maximum}\)
\(\text{a local maximum}\)
\(\text{none of these}\)
\(\text{a saddle point}\)
Consider the three points \((5,1)\text{,}\) \((7,3)\text{,}\) and \((9,4)\text{.}\)
(a) Supposed that at \((5,1)\text{,}\) we know that \(f_x=f_y=0\) and \(f_{xx} = 0\text{,}\) \(f_{yy} = 0\text{,}\) and \(f_{xy} > 0\text{.}\) What can we conclude about the behavior of this function near the point \((5,1)\text{?}\)
- (5,1) is a local maximum
- (5,1) is a local minimum
- (5,1) is a saddle point
- (5,1) is a none of these
(b) Supposed that at \((7,3)\text{,}\) we know that \(f_x=f_y=0\) and \(f_{xx} > 0\text{,}\) \(f_{yy} \lt 0\text{,}\) and \(f_{xy} = 0\text{.}\) What can we conclude about the behavior of this function near the point \((7,3)\text{?}\)
- (7,3) is a local maximum
- (7,3) is a local minimum
- (7,3) is a saddle point
- (7,3) is a none of these
(c) Supposed that at \((9,4)\text{,}\) we know that \(f_x=f_y=0\) and \(f_{xx} \lt 0\text{,}\) \(f_{yy} = 0\text{,}\) and \(f_{xy} > 0\text{.}\) What can we conclude about the behavior of this function near the point \((9,4)\text{?}\)
- (9,4) is a local maximum
- (9,4) is a local minimum
- (9,4) is a saddle point
- (9,4) is a none of these
Using this information, on a separate sheet of paper sketch a possible contour diagram for \(f\text{.}\)
\(\text{(5,1) is a saddle point}\)
\(\text{(7,3) is a saddle point}\)
\(\text{(9,4) is a saddle point}\)
Find three positive real numbers whose sum is 94 and whose product is a maximum.
Enter the three numbers separated by commas:
\(31.3333, 31.3333, 31.3333\)
A closed rectangular box has volume \(22\,\mbox{cm}^3\text{.}\) What are the lengths of the edges giving the minimum surface area?
lengths =
(Give the three lengths as a comma separated list.)
\(2.80204, 2.80204, 2.80204\)
An open rectangular box has volume \(26 \mbox{ cm}^3\text{.}\) What are the lengths of the edges giving the minimum surface area?
lengths =
(Give the three lengths as a comma separated list.)
\(3.73251, 3.73251, 1.86626\)
What is the shortest distance from the surface \(x y + 6 x + z^2 = 41\) to the origin?
distance =
\(\sqrt{29}\)
Find the volume of the largest rectangular box with edges parallel to the axes that can be inscribed in the ellipsoid
Hint: By symmetry, you can restrict your attention to the first octant (where \(x, y, z \ge 0\)), and assume your volume has the form \(V = 8xyz\text{.}\) Then arguing by symmetry, you need only look for points which achieve the maximum which lie in the first octant.
Maximum volume:
\(110.851251684408\)
Design a rectangular milk carton box of width \(w\text{,}\) length \(l\text{,}\) and height \(h\) which holds \(500 \mbox{ cm}^3\) of milk. The sides of the box cost \(1 \ \mbox{cent}/\mbox{cm}^2\) and the top and bottom cost \(2\ \mbox{cent}/\mbox{cm}^2\text{.}\) Find the dimensions of the box that minimize the total cost of materials used.
dimensions =
(Enter your answer as a comma separated list of lengths.)
\(12.5992, 6.2996, 6.29962\)
Respond to each of the following prompts to solve the given optimization problem.
- Let \(f(x,y) = \sin(x)+\cos(y)\text{.}\) Determine the absolute maximum and minimum values of \(f\text{.}\) At what points do these extreme values occur?
- For a certain differentiable function \(F\) of two variables \(x\) and \(y\text{,}\) its partial derivatives are
\[ F_x(x,y) = x^2-y-4 \ \ \mbox{and} \ \ F_y(x,y) = -x + y - 2. \nonumber \]
Find each of the critical points of \(F\text{,}\) and classify each as a local maximum, local minimum, or a saddle point.
- Determine all critical points of \(T(x,y) = 48 + 3xy - x^2y - xy^2\) and classify each as a local maximum, local minimum, or saddle point.
- Find and classify all critical points of \(g(x,y) = \frac{x^2}{2} + 3y^3 + 9y^2 - 3xy + 9y - 9x\)
- Find and classify all critical points of \(z = f(x,y) = ye^{-x^2-2y^2}\text{.}\)
- Determine the absolute maximum and absolute minimum of \(f(x,y) = 2 + 2x + 2y - x^2 - y^2\) on the triangular plate in the first quadrant bounded by the lines \(x = 0\text{,}\) \(y = 0\text{,}\) and \(y = 9-x\text{.}\)
- Determine the absolute maximum and absolute minimum of \(f(x,y) = 2 + 2x + 2y - x^2 - y^2\) over the closed disk of points \((x,y)\) such that \((x-1)^2 + (y-1)^2 \le 1\text{.}\)
- Find the point on the plane \(z = 6 - 3x - 2y\) that lies closest to the origin.
If a continuous function \(f\) of a single variable has two critical numbers \(c_1\) and \(c_2\) at which \(f\) has relative maximum values, then \(f\) must have another critical number \(c_3\text{,}\) because "it is impossible to have two mountains without some sort of valley in between. The other critical point can be a saddle point (a pass between the mountains) or a local minimum (a true valley)." (From Calculus in Vector Spaces by Lawrence J. Corwin and Robert H. Szczarb.) Consider the function \(f\) defined by \(f(x,y) = 4x^2e^y -2x^4 -e^{4y}\text{.}\) (From Ira Rosenholz in the Problems Section of the Mathematics Magazine, Vol. 60 NO. 1, February 1987.) Show that \(f\) has exactly two critical points, and that \(f\) has relative maximum values at each of these critical points. Explain how this function \(f\) illustrates that it really is possible to have two mountains without some sort of valley in between. Use appropriate technology to draw the surface defined by \(f\) to see graphically how this happens.
If a continuous function \(f\) of a single variable has exactly one critical number with a relative maximum at that critical point, then the value of \(f\) at that critical point is an absolute maximum. In this exercise we see that the same is not always true for functions of two variables. Let \(f(x,y) = 3xe^y-x^3-e^{3y}\) (from “The Only Critical Point in Town” Test by Ira Rosenholz and Lowell Smylie in the Mathematics Magazine, VOL 58 NO 3 May 1985.). Show that \(f\) has exactly one critical point, has a relative maximum value at that critical point, but that \(f\) has no absolute maximum value. Use appropriate technology to draw the surface defined by \(f\) to see graphically how this happens.
A manufacturer wants to procure rectangular boxes to ship its product. The boxes must contain 20 cubic feet of space. To be durable enough to ensure the safety of the product, the material for the sides of the boxes will cost $0.10 per square foot, while the material for the top and bottom will cost $0.25 per square foot. In this activity we will help the manufacturer determine the box of minimal cost.
- What quantities are constant in this problem? What are the variables in this problem? Provide appropriate variable labels. What, if any, restrictions are there on the variables?
- Using your variables from (a), determine a formula for the total cost \(C\) of a box.
- Your formula in part (b) might be in terms of three variables. If so, find a relationship between the variables, and then use this relationship to write \(C\) as a function of only two independent variables.
- Find the dimensions that minimize the cost of a box. Be sure to verify that you have a minimum cost.
A rectangular box with length \(x\text{,}\) width \(y\text{,}\) and height \(z\) is being built. The box is positioned so that one corner is stationed at the origin and the box lies in the first octant where \(x\text{,}\) \(y\text{,}\) and \(z\) are all positive. There is an added constraint on how the box is constructed: it must fit underneath the plane with equation \(x + 2y + 3z = 6\text{.}\) In fact, we will assume that the corner of the box “opposite” the origin must actually lie on this plane. The basic problem is to find the maximum volume of the box.
- Sketch the plane \(x + 2y + 3z = 6\text{,}\) as well as a picture of a potential box. Label everything appropriately.
- Explain how you can use the fact that one corner of the box lies on the plane to write the volume of the box as a function of \(x\) and \(y\) only. Do so, and clearly show the formula you find for \(V(x,y)\text{.}\)
- Find all critical points of \(V\text{.}\) (Note that when finding the critical points, it is essential that you factor first to make the algebra easier.)
- Without considering the current applied nature of the function \(V\text{,}\) classify each critical point you found above as a local maximum, local minimum, or saddle point of \(V\text{.}\)
- Determine the maximum volume of the box, justifying your answer completely with an appropriate discussion of the critical points of the function.
- Now suppose that we instead stipulated that, while the vertex of the box opposite the origin still had to lie on the plane, we were only going to permit the sides of the box, \(x\) and \(y\text{,}\) to have values in a specified range (given below). That is, we now want to find the maximum value of \(V\) on the closed, bounded region
\[ \frac{1}{2} \le x \le 1, \ \ 1 \le y \le 2. \nonumber \]
Find the maximum volume of the box under this condition, justifying your answer fully.
The airlines place restrictions on luggage that can be carried onto planes.
- A carry-on bag can weigh no more than 40 lbs.
- The length plus width plus height of a bag cannot exceed 45 inches.
- The bag must fit in an overhead bin.
Let \(x\text{,}\) \(y\text{,}\) and \(z\) be the length, width, and height (in inches) of a carry on bag. In this problem we find the dimensions of the bag of largest volume, \(V = xyz\text{,}\) that satisfies the second restriction. Assume that we use all 45 inches to get a maximum volume. (Note that this bag of maximum volume might not satisfy the third restriction.)
- Write the volume \(V=V(x,y)\) as a function of just the two variables \(x\) and \(y\text{.}\)
- Explain why the domain over which \(V\) is defined is the triangular region \(R\) with vertices (0,0), (45,0), and (0,45).
- Find the critical points, if any, of \(V\) in the interior of the region \(R\text{.}\)
- Find the maximum value of \(V\) on the boundary of the region \(R\text{,}\) and then determine the dimensions of a bag with maximum volume on the entire region \(R\text{.}\) (Note that most carry-on bags sold today measure \(22\) by \(14\) by \(9\) inches with a volume of \(2772\) cubic inches, so that the bags will fit into the overhead bins.)
According to The Song of Insects by G.W. Pierce (Harvard College Press, 1948) the sound of striped ground crickets chirping, in number of chirps per second, is related to the temperature. So the number of chirps per second could be a predictor of temperature. The data Pierce collected is shown in Table 10.7.11., where \(x\) is the (average) number of chirps per second and \(y\) is the temperature in degrees Fahrenheit.
A scatterplot of the data would show that, while the relationship between \(x\) and \(y\) is not exactly linear, it looks to have a linear pattern. It could be that the relationship is really linear but experimental error causes the data to be slightly inaccurate. Or perhaps the data is not linear, but only approximately linear.
| \(x\) | \(y\) |
|---|---|
| \(20.0\) | \(88.6\) |
| \(16.0\) | \(71.6\) |
| \(19.8\) | \(93.3\) |
| \(18.4\) | \(84.3\) |
| \(17.1\) | \(80.6\) |
| \(15.5\) | \(75.2\) |
| \(14.7\) | \(69.7\) |
| \(17.1\) | \(82.0\) |
| \(15.4\) | \(69.4\) |
| \(16.2\) | \(83.3\) |
| \(15.0\) | \(79.6\) |
| \(17.2\) | \(82.6\) |
| \(16.0\) | \(80.6\) |
| \(17.0\) | \(83.5\) |
| \(14.4\) | \(76.3\) |
If we want to use the data to make predications, then we need to fit a curve of some kind to the data. Since the cricket data appears roughly linear, we will fit a linear function \(f\) of the form \(f(x) = mx+b\) to the data. We will do this in such a way that we minimize the sums of the squares of the distances between the \(y\) values of the data and the corresponding \(y\) values of the line defined by \(f\text{.}\) This type of fit is called a least squares approximation. If the data is represented by the points \((x_1,y_1)\text{,}\) \((x_2,y_2)\text{,}\) \(\ldots\text{,}\) \((x_n,y_n)\text{,}\) then the square of the distance between \(y_i\) and \(f(x_i)\) is \((f(x_i)-y_i)^2 = (mx_i+b-y_i)^2\text{.}\) So our goal is to minimize the sum of these squares, of minimize the function \(S\) defined by
\[ S(m,b) = \sum_{i=1}^n (mx_i+b-y_i)^2. \nonumber \]
- Calculate \(S_m\) and \(S_b\text{.}\)
- Solve the system \(S_m(m,b) = 0\) and \(S_b(m,b) = 0\) to show that the critical point satisfies
\begin{align*} m & = \frac{n\left(\sum_{i=1}^n x_iy_i\right) - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n y_i \right)}{n\left(\sum_{i=1}^n x_i^2 \right) - \left(\sum_{i=1}^n x_i \right)^2}\\[4pt] b & = \frac{\left(\sum_{i=1}^n y_i\right) \left(\sum_{i=1}^n x_i^2\right) - \left(\sum_{i=1}^n x_i \right) \left(\sum_{i=1}^n x_iy_i \right)}{n\left(\sum_{i=1}^n x_i^2 \right) - \left(\sum_{i=1}^n x_i \right)^2}. \end{align*}
(Hint: Don't be daunted by these expressions, the system \(S_m(m,b) = 0\) and \(S_b(m,b) = 0\) is a system of two linear equations in the unknowns \(m\) and \(b\text{.}\) It might be easier to let \(r=\sum_{i=1}^n x_i^2\text{,}\) \(s=\sum_{i=1}^n x_i\text{,}\) \(t = \sum_{i=1}^n y_i\text{,}\) and \(u = \sum_{i=1}^n x_iy_i\) and write your equations using these constants.)
- Use the Second Derivative Test to explain why the critical point gives a local minimum. Can you then explain why the critical point gives an absolute minimum?
- Use the formula from part (b) to find the values of \(m\) and \(b\) that give the line of best fit in the least squares sense to the cricket data. Draw your line on the scatter plot to convince yourself that you have a well-fitting line.
10.8: Constrained Optimization- Lagrange Multipliers
Exercises 10.8.3 Exercises
Use Lagrange multipliers to find the maximum and minimum values of \(f(x,y) = 3 x - 4 y\) subject to the constraint \(x^2 + 3 y^2 = 129\text{,}\) if such values exist.
maximum =
minimum =
(For either value, enter DNE if there is no such value.)
\(3\cdot 3\cdot 3+4\cdot 4\)
\(-3\cdot 3\cdot 3-4\cdot 4\)
Use Lagrange multipliers to find the maximum and minimum values of \(f(x,y) = x^2 y + 3 y^2 - y\text{,}\) subject to the constraint \(x^2 + y^2 \leq 38.3333333333333\)
maximum =
minimum =
(For either value, enter DNE if there is no such value.)
\(137.926\)
\(-59.2593\)
Find the absolute maximum and minimum of the function \(f(x,y) = x^2 + y^2\) subject to the constraint \(x^4 + y^4 = 6561\text{.}\)
As usual, ignore unneeded answer blanks, and list points in lexicographic order.
Absolute minimum value:
attained at (, ), (, ),
(, ), (, ).
Absolute maximum value:
attained at (, ), (, ),
(, ), (, ).
\(81\)
\(-9\)
\(0\)
\(0\)
\(-9\)
\(0\)
\(9\)
\(9\)
\(0\)
\(114.551298552221\)
\(-7.56806773728343\)
\(-7.56806773728343\)
\(-7.56806773728343\)
\(7.56806773728343\)
\(7.56806773728343\)
\(-7.56806773728343\)
\(7.56806773728343\)
\(7.56806773728343\)
Find the absolute maximum and minimum of the function \(f(x,y) = x^2 - y^2\) subject to the constraint \(x^2 + y^2 = 361\text{.}\)
As usual, ignore unneeded answer blanks, and list points in lexicographic order.
Absolute minimum value:
attained at (, ) and (, ).
Absolute maximum value:
attained at (, ) and (, ).
\(-361\)
\(0\)
\(-19\)
\(0\)
\(19\)
\(361\)
\(-19\)
\(0\)
\(19\)
\(0\)
Find the minimum distance from the point \((1,1,11)\) to the paraboloid given by the equation \(z=x^2+y^2\text{.}\)
Minimum distance =
Note: If you need to find roots of a polynomial of degree \(\geq 3\text{,}\) you may want to use a calculator of computer to do so numerically. Also be sure that you can give a geometric justification for your answer.
\(\sqrt{3.53771}\)
For each value of \(\lambda\) the function \(h(x,y) = x^2 + y^2 - \lambda(2 x + 8 y - 20)\) has a minimum value \(m(\lambda)\text{.}\)
(a) Find \(m(\lambda)\)
\(m(\lambda) =\)
(Use the letter L for \(\lambda\) in your expression.)
(b) For which value of \(\lambda\) is \(m(\lambda)\) the largest, and what is that maximum value?
\(\lambda =\)
maximum \(m(\lambda) =\)
(c) Find the minimum value of \(f(x,y)=x^2+y^2\) subject to the constraint \(2 x + 8 y = 20\) using the method of Lagrange multipliers and evaluate \(\lambda\text{.}\)
minimum \(f\) =
\(\lambda =\)
(How are these results related to your result in part (b)?)
\(20L-\frac{\left(2\cdot 2+8\cdot 8\right)L^{2}}{4}\)
\(\frac{2\cdot 20}{2\cdot 2+8\cdot 8}\)
\(\frac{20\cdot 20}{2\cdot 2+8\cdot 8}\)
\(\frac{20\cdot 20}{2\cdot 2+8\cdot 8}\)
\(\frac{2\cdot 20}{2\cdot 2+8\cdot 8}\)
The plane \(x + y + 2z = 6\) intersects the paraboloid \(z = x^2 + y^2\) in an ellipse. Find the points on this ellipse that are nearest to and farthest from the origin.
Point farthest away occurs at
(, ,).
Point nearest occurs at
(, ,).
\(-1.5\)
\(-1.5\)
\(4.5\)
\(1\)
\(1\)
\(2\)
Find the maximum and minimum values of the function \(f(x,y,z) = x^2 y^2 z^2\) subject to the constraint \(x^2 + y^2 + z^2 = 64\text{.}\)
Maximum value is , occuring at points (positive integer or "infinitely many").
Minimum value is , occuring at points (positive integer or "infinitely many").
\(9709.03703703704\)
\(8\)
\(0\)
infinitely many
Find the maximum and minimum values of the function \(f(x,y,z,t) = x+y+z+t\) subject to the constraint \(x^2 + y^2 + z^2 + t^2 = 100\text{.}\)
Maximum value is , occuring at points (positive integer or "infinitely many").
Minimum value is , occuring at points (positive integer or "infinitely many").
\(20\)
\(1\)
\(-20\)
\(1\)
Find the maximum and minimum volumes of a rectangular box whose surface area equals 7000 square cm and whose edge length (sum of lengths of all edges) is 440 cm.
Hint: It can be deduced that the box is not a cube, so if x, y, and z are the lengths of the sides, you may want to let x represent a side with \(x \ne y\) and \(x \ne z\text{.}\)
Maximum value is ,
occuring at (, ,).
Minimum value is ,
occuring at (, ,).
\(34481.4814814815\)
\(63.3333333333333\)
\(23.3333333333333\)
\(23.3333333333333\)
\(25000\)
\(10\)
\(50\)
\(50\)
(a) If \(\sum_{i=1}^3 x_i = 4\text{,}\) find the values of \(x_1, x_2, x_3\) making \(\sum_{i=1}^3 {x_i}^2\) minimum.
\(x_1, x_2, x_3 =\)
(Give your values as a comma separated list.)
(b) Generalize the result of part (a) to find the minimum value of \(\sum_{i=1}^n{x_i}^2\) subject to \(\sum_{i=1}^n x_i=4\text{.}\)
minimum value =
\(1.33333, 1.33333, 1.33333\)
\(\frac{4\cdot 4}{n}\)
The Cobb-Douglas production function is used in economics to model production levels based on labor and equipment. Suppose we have a specific Cobb-Douglas function of the form
where \(x\) is the dollar amount spent on labor and \(y\) the dollar amount spent on equipment. Use the method of Lagrange multipliers to determine how much should be spent on labor and how much on equipment to maximize productivity if we have a total of 1.5 million dollars to invest in labor and equipment.
Use the method of Lagrange multipliers to find the point on the line \(x-2y=5\) that is closest to the point \((1,3)\text{.}\) To do so, respond to the following prompts.
- Write the function \(f=f(x,y)\) that measures the square of the distance from \((x,y)\) to \((1,3)\text{.}\) (The extrema of this function are the same as the extrema of the distance function, but \(f(x,y)\) is simpler to work with.)
- What is the constraint \(g(x,y) = c\text{?}\)
- Write the equations resulting from \(\nabla f = \lambda \nabla g\) and the constraint. Find all the points \((x,y)\) satisfying these equations.
- Test all the points you found to determine the extrema.
Apply the Method of Lagrange Multipliers solve each of the following constrained optimization problems.
- Determine the absolute maximum and absolute minimum values of \(f(x,y) = (x-1)^2 + (y-2)^2\) subject to the constraint that \(x^2 + y^2 = 16\text{.}\)
- Determine the points on the sphere \(x^2 + y^2 + z^2 = 4\) that are closest to and farthest from the point \((3,1,-1)\text{.}\) (As in the preceding exercise, you may find it simpler to work with the square of the distance formula, rather than the distance formula itself.)
- Find the absolute maximum and minimum of \(f(x,y,z) = x^2 + y^2 + z^2\) subject to the constraint that \((x-3)^2 + (y+2)^2 + (z-5)^2 \le 16\text{.}\) (Hint: here the constraint is a closed, bounded region. Use the boundary of that region for applying Lagrange Multipliers, but don't forget to also test any critical values of the function that lie in the interior of the region.)
In this exercise we consider how to apply the Method of Lagrange Multipliers to optimize functions of three variable subject to two constraints. Suppose we want to optimize \(f = f(x,y,z)\) subject to the constraints \(g(x,y,z) = c\) and \(h(x,y,z) = k\text{.}\) Also suppose that the two level surfaces \(g(x,y,z) = c\) and \(h(x,y,z) = k\) intersect at a curve \(C\text{.}\) The optimum point \(P = (x_0,y_0,z_0)\) will then lie on \(C\text{.}\)
- Assume that \(C\) can be represented parametrically by a vector-valued function \(\mathbf{r} = \mathbf{r}(t)\text{.}\) Let \(\overrightarrow{OP} = \mathbf{r}(t_0)\text{.}\) Use the Chain Rule applied to \(f(\mathbf{r}(t))\text{,}\) \(g(\mathbf{r}(t))\text{,}\) and \(h(\mathbf{r}(t))\text{,}\) to explain why
\begin{align*} \nabla f(x_0,y_0,z_0) \cdot \mathbf{r}'(t_0) & = 0, \\[4pt] \nabla g(x_0,y_0,z_0) \cdot \mathbf{r}'(t_0) & = 0, \text{ and } \\[4pt] \nabla h(x_0,y_0,z_0) \cdot \mathbf{r}'(t_0) & = 0. \end{align*}
Explain how this shows that \(\nabla f(x_0,y_0,z_0)\text{,}\) \(\nabla g(x_0,y_0,z_0)\text{,}\) and \(\nabla h(x_0,y_0,z_0)\) are all orthogonal to \(C\) at \(P\text{.}\) This shows that \(\nabla f(x_0,y_0,z_0)\text{,}\) \(\nabla g(x_0,y_0,z_0)\text{,}\) and \(\nabla h(x_0,y_0,z_0)\) all lie in the same plane.
- Assuming that \(\nabla g(x_0,y_0,z_0)\) and \(\nabla h(x_0,y_0,z_0)\) are nonzero and not parallel, explain why every point in the plane determined by \(\nabla g(x_0,y_0,z_0)\) and \(\nabla h(x_0,y_0,z_0)\) has the form \(s\nabla g(x_0,y_0,z_0)+t\nabla h(x_0,y_0,z_0)\) for some scalars \(s\) and \(t\text{.}\)
- Parts (a.) and (b.) show that there must exist scalars \(\lambda\) and \(\mu\) such that
\[ \nabla f(x_0,y_0,z_0) = \lambda \nabla g(x_0,y_0,z_0)+ \mu \nabla h(x_0,y_0,z_0). \nonumber \]
So to optimize \(f = f(x,y,z)\) subject to the constraints \(g(x,y,z) = c\) and \(h(x,y,z) = k\) we must solve the system of equations
\begin{align*} \nabla f(x,y,z) & = \lambda \nabla g(x,y,z)+ \mu \nabla h(x,y,z), \\[4pt] g(x,y,z) & = c, \text{ and } \\[4pt] h(x,y,z) & = k. \end{align*}for \(x\text{,}\) \(y\text{,}\) \(z\text{,}\) \(\lambda\text{,}\) and \(\mu\text{.}\)
Use this idea to find the maximum and minium values of \(f(x,y,z) = x+2y\) subject to the constraints \(y^2+z^2=8\) and \(x+y+z = 10\text{.}\)
There is a useful interpretation of the Lagrange multiplier \(\lambda\text{.}\) Assume that we want to optimize a function \(f\) with constraint \(g(x,y)=c\text{.}\) Recall that an optimal solution occurs at a point \((x_0, y_0)\) where \(\nabla f = \lambda \nabla g\text{.}\) As the constraint changes, so does the point at which the optimal solution occurs. So we can think of the optimal point as a function of the parameter \(c\text{,}\) that is \(x_0 = x_0(c)\) and \(y_0=y_0(c)\text{.}\) The optimal value of \(f\) subject to the constraint can then be considered as a function of \(c\) defined by \(f(x_0(c), y_0(c))\text{.}\) The Chain Rule shows that
- Use the fact that \(\nabla f = \lambda \nabla g\) at \((x_0,y_0)\) to explain why
\[ \frac{df}{dc} = \lambda \frac{dg}{dc}. \nonumber \]
- Use the fact that \(g(x,y) = c\) to show that
\[ \frac{df}{dc} = \lambda. \nonumber \]
Conclude that \(\lambda\) tells us the rate of change of the function \(f\) as the parameter \(c\) increases (or by approximately how much the optimal value of the function \(f\) will change if we increase the value of \(c\) by 1 unit).
- Suppose that \(\lambda = 324\) at the point where the package described in Preview Activity 10.8.1 has its maximum volume. Explain in context what the value \(324\) tells us about the package.
- Suppose that the maximum value of a function \(f = f(x,y)\) subject to a constraint \(g(x,y) = 100\) is \(236\text{.}\) When using the method of Lagrange multipliers and solving \(\nabla f = \lambda \nabla g\text{,}\) we obtain a value of \(\lambda = 15\) at this maximum. Find an approximation to the maximum value of \(f\) subject to the constraint \(g(x,y) = 98\text{.}\)


