11E: Multiple Integrals

Last updated
Save as PDF

Page ID: 108401

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

11.1: Double Riemann Sums and Double Integrals over Rectangles

1.

Suppose $f(x,y) = 25-x^{2}-y^{2}$ and $R$ is the rectangle with vertices (0,0), (6,0), (6,4), (0,4). In each part, estimate $\displaystyle \iint\limits_R f(x,y) \, dA$ using Riemann sums. For underestimates or overestimates, consistently use either the lower left-hand corner or the upper right-hand corner of each rectangle in a subdivision, as appropriate.

(a) Without subdividing $R\text{,}$

Underestimate =

Overestimate =

(b) By partitioning $R$ into four equal-sized rectangles.

Underestimate =

Overestimate =

Answer. 1

$-648$

Answer. 2

$600$

Answer. 3

$-180$

Answer. 4

$444$

2.

Consider the solid that lies above the square (in the $xy$-plane) $R = [0, 1] \times [0, 1]\text{,}$ and below the elliptic paraboloid $z = 100 - x^2+ 6 xy - 3 y^2\text{.}$

Estimate the volume by dividing $R$ into 9 equal squares and choosing the sample points to lie in the midpoints of each square.

Answer.

$100.203703703704$

3.

Let $R$ be the rectangle with vertices $(0,0)\text{,}$ $(2,0)\text{,}$ $(2,2)\text{,}$ and $(0,2)$ and let $f(x,y) = \sqrt{0.333333xy}\text{.}$

(a) Find reasonable upper and lower bounds for $\int_{R}f\,dA$ without subdividing $R\text{.}$

upper bound =

lower bound =

(b) Estimate $\int_{R}f\,dA$ three ways: by partitioning $R$ into four subrectangles and evaluating $f$ at its maximum and minimum values on each subrectangle, and then by considering the average of these (over and under) estimates.

overestimate: $\int_{R}f\,dA \approx$

underestimate: $\int_{R}f\,dA \approx$

average: $\int_{R}f\,dA \approx$

Answer. 1

$4\sqrt{\frac{1}{3}\cdot 2\cdot 2}$

Answer. 2

$0$

Answer. 3

$\frac{4}{4}\!\left(\sqrt{\frac{\frac{1}{3}\cdot 4}{4}}+2\sqrt{\frac{\frac{1}{3}\cdot 4}{2}}+\sqrt{\frac{1}{3}\cdot 4}\right)$

Answer. 4

$\frac{4}{4}\sqrt{\frac{\frac{1}{3}\cdot 4}{4}}$

Answer. 5

$\frac{4}{8}\!\left(2\sqrt{\frac{\frac{1}{3}\cdot 4}{4}}+2\sqrt{\frac{\frac{1}{3}\cdot 4}{2}}+\sqrt{\frac{1}{3}\cdot 4}\right)$

4.

Using Riemann sums with four subdivisions in each direction, find upper and lower bounds for the volume under the graph of $f(x,y) = 6+3xy$ above the rectangle $R$ with $0\le x\le 1,\quad 0\le y \le 6\text{.}$

upper bound =

lower bound =

Answer. 1

$0.25\cdot 1.5\cdot 208.5$

Answer. 2

$0.25\cdot 1.5\cdot 136.5$

5.

Consider the solid that lies above the square (in the xy-plane) $R = [0, 2] \times [0, 2]\text{,}$

and below the elliptic paraboloid $z = 36 - x^{2} - 2y^2\text{.}$

(A) Estimate the volume by dividing R into 4 equal squares and choosing the sample points to lie in the lower left hand corners.

(B) Estimate the volume by dividing R into 4 equal squares and choosing the sample points to lie in the upper right hand corners..

Answer. 1

$138$

Answer. 2

$114$

Answer. 3

$126$

6.

The figure below shows contours of $g(x,y)$ on the region $R\text{,}$ with $5 \le x\le 11$ and $2 \le y\le 8\text{.}$

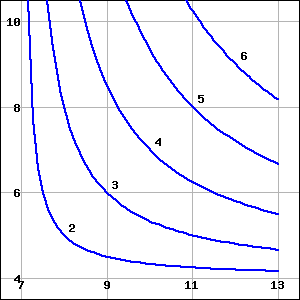
$webwork-186-image-1.png$

Using $\Delta x = \Delta y =2\text{,}$ find an overestimate and an underestimate for $\int_R g(x,y)\, dA\text{.}$

Overestimate =

Underestimate =

Answer. 1

$\left(4+4+4+4+2+2+4+2+0\right)\cdot 2\cdot 2$

Answer. 2

$\left(2+1+0+1+0+-1+0+-1+-2\right)\cdot 2\cdot 2$

7.

The figure below shows the distribution of temperature, in degrees C, in a 5 meter by 5 meter heated room.

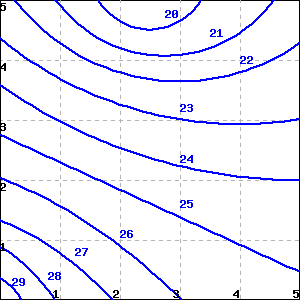
$webwork-187-image-1-1.png$

Using Riemann sums, estimate the average temperature in the room.

average temperature =

Answer.

$\frac{667+621}{50}$

8.

Values of $f(x,y)$ are given in the table below. Let $R$ be the rectangle $1 \leq x \leq 1.6, 2 \leq y \leq 3.2\text{.}$ Find a Riemann sum which is a reasonable estimate for $\int_R f(x,y) \, da$ with $\Delta x = 0.2$ and $\Delta y = 0.4\text{.}$ Note that the values given in the table correspond to midpoints.

\[ \begin{array}{|c || c|c|c|} \hline y \backslash x & 1.1 & 1.3 & 1.5 \\[4pt] \hline \hline 2.2 & 4 & 2 & -1 \\[4pt] \hline 2.6 & 5 & 2 & 0 \\[4pt] \hline 3.0 & 9 & -5 & 0 \\[4pt] \hline \end{array} \nonumber \]

$\int_R f(x,y) \, da \approx$

Answer.

$1.28$

9.

Values of $f(x,y)$ are shown in the table below.

	$x = 3$	$x = 3.3$	$x = 3.6$
$y = 4$	7	9	12
$y = 4.4$	5	7	9
$y = 4.8$	3	5	18

Let $R$ be the rectangle $3 \leq x \leq 3.6\text{,}$ $4 \leq y \leq 4.8\text{.}$ Find the values of Riemann sums which are reasonable over- and under-estimates for $\int_R f(x,y) \,dA$ with $\Delta x=0.3$ and $\Delta y=0.4\text{.}$

over-estimate:

under-estimate:

Answer. 1

$46\cdot 0.3\cdot 0.4$

Answer. 2

$20\cdot 0.3\cdot 0.4$

10.

The temperature at any point on a metal plate in the $xy$ plane is given by $T(x,y) = 100-4x^2 - y^2\text{,}$ where $x$ and $y$ are measured in inches and $T$ in degrees Celsius. Consider the portion of the plate that lies on the rectangular region $R = [1,5] \times [3,6]\text{.}$

Estimate the value of $\iint_R T(x,y) \, dA$ by using a double Riemann sum with two subintervals in each direction and choosing $(x_i^*, y_j^*)$ to be the point that lies in the upper right corner of each subrectangle.
Determine the area of the rectangle $R\text{.}$
Estimate the average temperature, $T_{\operatorname{AVG}(R)}\text{,}$ over the region $R\text{.}$
Do you think your estimate in (c) is an over- or under-estimate of the true temperature? Why?

11.

Let $f$ be a function of independent variables $x$ and $y$ that is increasing in both the positive $x$ and $y$ directions on a rectangular domain $R\text{.}$ For each of the following situations, determine if the double Riemann sum of $f$ over $R$ is an overestimate or underestimate of the double integral $\iint_R f(x,y) \, dA\text{,}$ or if it impossible to determine definitively. Provide justification for your responses.

The double Riemann sum of $f$ over $R$ where $f$ is evaluated at the lower left point of each subrectangle.
The double Riemann sum of $f$ over $R$ where $f$ is evaluated at the upper right point of each subrectangle.
The double Riemann sum of $f$ over $R$ where $f$ is evaluated at the midpoint of each subrectangle.
The double Riemann sum of $f$ over $R$ where $f$ is evaluated at the lower right point of each subrectangle.

12.

The wind chill, as frequently reported, is a measure of how cold it feels outside when the wind is blowing. In Table 11.1.10, the wind chill $w=w(v,T)\text{,}$ measured in degrees Fahrenheit, is a function of the wind speed $v\text{,}$ measured in miles per hour, and the ambient air temperature $T\text{,}$ also measured in degrees Fahrenheit. Approximate the average wind chill on the rectangle $[5,35] \times [-20,20]$ using 3 subintervals in the $v$ direction, 4 subintervals in the $T$ direction, and the point in the lower left corner in each subrectangle.

Table 11.1.10. Wind chill as a function of wind speed and temperature.

$v \backslash T$	$-20$	$-15$	$-10$	$-5$	$0$	$5$	$10$	$15$	$20$
$5$	$-34$	$-28$	$-22$	$-16$	$-11$	$-5$	$1$	$7$	$13$
$10$	$-41$	$-35$	$-28$	$-22$	$-16$	$-10$	$-4$	$3$	$9$
$15$	$-45$	$-39$	$-32$	$-26$	$-19$	$-13$	$-7$	$0$	$6$
$20$	$-48$	$-42$	$-35$	$-29$	$-22$	$-15$	$-9$	$-2$	$4$
$25$	$-51$	$-44$	$-37$	$-31$	$-24$	$-17$	$-11$	$-4$	$3$
$30$	$-53$	$-46$	$-39$	$-33$	$-26$	$-19$	$-12$	$-5$	$1$
$35$	$-55$	$-48$	$-41$	$-34$	$-27$	$-21$	$-14$	$-7$	$0$

13.

Consider the box with a sloped top that is given by the following description: the base is the rectangle $R = [0,4] \times [0,3]\text{,}$ while the top is given by the plane $z = p(x,y) = 20 - 2x - 3y\text{.}$

Estimate the value of $\iint_R p(x,y) \, dA$ by using a double Riemann sum with four subintervals in the $x$ direction and three subintervals in the $y$ direction, and choosing $(x_i^*, y_j^*)$ to be the point that is the midpoint of each subrectangle.
What important quantity does your double Riemann sum in (a) estimate?
Suppose it can be determined that $\iint_R p(x,y) \, dA = 138\text{.}$ What is the exact average value of $p$ over $R\text{?}$
If you wanted to build a rectangular box (with the same base) that has the same volume as the box with the sloped top described here, how tall would the rectangular box have to be?

11.2: Iterated Integrals

1.

Evaluate the iterated integral $\int_{0}^{4} \int_{0}^{4} 12x^2y^3 \, dx dy$

Answer.

$16384$

2.

Evaluate the iterated integral $\int_{4}^{5} \int_{2}^{3} (3x + y)^{-2} \: dy dx$

Answer.

$0.00394481921566777$

3.

Find $\int_{0}^{1} \int_{9}^{13}( x + \ln y) \,dydx$

Answer.

$11.569320450974$

4.

Find $\int_{0}^{5} \int_{2}^{4} xy e^{x+y} \,dydx$

Answer.

$93006.8798911913$

5.

Calculate the double integral $\int \int_{\mathbf{R}} (4x + 4y + 16 )\: dA$ where $\mathbf{R}$ is the region: $0 \leq x \leq 2, 0 \leq y \leq 2\text{.}$

Answer.

$96$

6.

Calculate the double integral $\int \int_{\mathbf{R}} x \cos(x + y) \: dA$ where $\bf{R}$ is the region: $0 \leq x \leq \frac{\pi}{6}, 0 \leq y \leq \frac{\pi}{4}$

Answer.

$0.0767515510438744$

7.

Consider the solid that lies above the square (in the xy-plane) $R = [0, 2] \times [0, 2]\text{,}$

and below the elliptic paraboloid $z = 49 - x^{2} - 3y^2\text{.}$

(A) Estimate the volume by dividing R into 4 equal squares and choosing the sample points to lie in the lower left hand corners.

(B) Estimate the volume by dividing R into 4 equal squares and choosing the sample points to lie in the upper right hand corners..

(D) Using iterated integrals, compute the exact value of the volume.

Answer. 1

$188$

Answer. 2

$156$

Answer. 3

$172$

Answer. 4

$174.666666666667$

8.

If $\displaystyle \int_{1}^{3} f(x) \: dx = -2$ and $\displaystyle \int_{-5}^{-4} g(x) \: dx = 4\text{,}$ what is the value of $\displaystyle \int\!\!\int_{D} f(x)\!g(y) \: dA$ where $D$ is the rectangle: $1 \leq x \leq 3, \ \ -5 \leq y \leq -4\text{?}$

Answer.

$-8$

9.

Find the average value of $f(x,y) = 4 x^6 y^3$ over the rectangle R with vertices $(-3,0), (-3,6), (3,0), (3,6)\text{.}$

Average value =

Answer.

$22494.8571428571$

10.

Find the average value of $f(x,y) = 7 e^{ y} \sqrt{x+e^{ y}}$ over the rectangle $R = [0,8] \times [0,5]\text{.}$

Average value =

Answer.

$1745.04372328632$

11.

Evaluate each of the following double or iterated integrals exactly.

$\displaystyle \int_1^3 \left( \int_2^5 xy \, dy \right) \, dx$
$\displaystyle \int_0^{\pi/4} \left( \int_0^{\pi/3} \sin(x) \cos(y) \, dx \right) \, dy$
$\displaystyle \int_0^1 \left( \int_0^1 e^{-2x - 3y} \, dy \right) \, dx$
$\iint_R \sqrt{2x + 5y} \, dA\text{,}$ where $R = [0,2]\times[0,3]\text{.}$

12.

Write an iterated integral whose value represents the volume under the surface $T$ over the rectangle $R\text{.}$
Evaluate the iterated integral you determined in (a).
Find the area of the rectangle, $R\text{.}$
Determine the exact average temperature, $T_{\operatorname{AVG}(R)}\text{,}$ over the region $R\text{.}$

13.

Consider the box with a sloped top that is given by the following description: the base is the rectangle $R = [1,4] \times [2,5]\text{,}$ while the top is given by the plane $z = p(x,y) = 30 - x - 2y\text{.}$

Write an iterated integral whose value represents the volume under $p$ over the rectangle $R\text{.}$
Evaluate the iterated integral you determined in (a).
What is the exact average value of $p$ over $R\text{?}$
If you wanted to build a rectangular box (with an identical base) that has the same volume as the box with the sloped top described here, how tall would the rectangular box have to be?

11.3: Double Integrals over General Regions

1.

Evaluate the double integral $\displaystyle I = \int\!\!\int_{\mathbf{D}} xy \: d\!A$ where $\mathbf{D}$ is the triangular region with vertices $(0, 0), (6, 0), (0, 2)\text{.}$

Answer.

$6$

2.

Evaluate the double integral $\displaystyle I = \int\!\!\int_{\mathbf{D}} xy \: d\!A$ where $\mathbf{D}$ is the triangular region with vertices $(0, 0), (1, 0), (0, 6)\text{.}$

Answer.

$1.5$

3.

Evaluate the integral by reversing the order of integration.

$\int_{0}^{1}\!\!\int_{3y}^{3} e^{x^{2}} \, dx dy =$

Answer.

$1350.34732126256$

4.

Decide, without calculation, if each of the integrals below are positive, negative, or zero. Let D be the region inside the unit circle centered at the origin. Let T, B, R, and L denote the regions enclosed by the top half, the bottom half, the right half, and the left half of unit circle, respectively.

$\displaystyle \displaystyle \iint\limits_T (y^3 + y^5) \, dA$
$\displaystyle \displaystyle \iint\limits_L (y^3 + y^5) \, dA$
$\displaystyle \displaystyle \iint\limits_D (y^3 + y^5) \, dA$
$\displaystyle \displaystyle \iint\limits_R (y^3 + y^5) \, dA$
$\displaystyle \displaystyle \iint\limits_B (y^3 + y^5) \, dA$

5.

The region $W$ lies below the surface $f(x,y) = 8 e^{-(x-3)^2-y^2}$ and above the disk $x^2+y^2\le 16$ in the $xy$-plane.

(a) Think about what the contours of $f$ look like. You may want to using $f(x,y)=1$ as an example. Sketch a rough contour diagram on a separate sheet of paper.

(b) Write an integral giving the area of the cross-section of $W$ in the plane $x=3\text{.}$

Area = $\int_a^b$ $d$,

where $a =$ and $b =$

(c) Use your work from (b) to write an iterated double integral giving the volume of $W\text{,}$ using the work from (b) to inform the construction of the inside integral.

Volume = $\int_a^b\int_c^d$ $d$ $d$,

where $a =$, $b =$ $c =$ and $d =$

Answer. 1

$8e^{-y^{2}}$

Answer. 2

$y$

Answer. 3

$-2.64575$

Answer. 4

$2.64575$

Answer. 5

$8e^{-\left(x-3\right)^{2}-y^{2}}$

Answer. 6

$y$

Answer. 7

$x$

Answer. 8

$-4$

Answer. 9

$4$

Answer. 10

$-\sqrt{16-x^{2}}$

Answer. 11

$\sqrt{16-x^{2}}$

6.

Set up a double integral in rectangular coordinates for calculating the volume of the solid under the graph of the function $f(x,y) = 22-x^{2}-y^{2}$ and above the plane $z = 6\text{.}$

Instructions: Please enter the integrand in the first answer box. Depending on the order of integration you choose, enter dx and dy in either order into the second and third answer boxes with only one dx or dy in each box. Then, enter the limits of integration.

$\displaystyle \int_A^B \int_C^D$

A =

B =

C =

D =

Answer.

$16-x^{2}-y^{2};\,dx;\,dy;\,-4;\,4;\,-\sqrt{16-y^{2}};\,\sqrt{16-y^{2}}$

7.

Find the volume of the solid bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 6.

Answer.

$36$

8.

Consider the integral $\displaystyle \int_0^6 \int_0^{\sqrt{36-y}} f(x,y) dx dy\text{.}$ If we change the order of integration we obtain the sum of two integrals:

$\displaystyle \int_a^b \int_{g_1(x)}^{g_2(x)} f(x,y) dy dx + \displaystyle \int_c^d \int_{g_3(x)}^{g_4(x)} f(x,y) dy dx$

$a =$ $b =$

$g_1(x) =$ $g_2(x) =$

$c =$ $d =$

$g_3(x) =$ $g_4(x) =$

Answer. 1

$0$

Answer. 2

$5.47722557505166$

Answer. 3

$0$

Answer. 4

$6$

Answer. 5

$5.47722557505166$

Answer. 6

$6$

Answer. 7

$0$

Answer. 8

$36-x^{2}$

9.

A pile of earth standing on flat ground has height 36 meters. The ground is the xy-plane. The origin is directly below the top of the pile and the z-axis is upward. The cross-section at height z is given by $x^2 + y^2 = 36 - z$ for $0 \leq z \leq 36\text{,}$ with $x, y,$ and $z$ in meters.

(a) What equation gives the edge of the base of the pile?

$\displaystyle x^2 + y^2 = 36$
$\displaystyle x + y = 36$
$\displaystyle x^2 + y^2 = 6$
$\displaystyle x + y = 6$
None of the above

(b) What is the area of the base of the pile?

$\displaystyle x^2 + y^2 = 25$
$\displaystyle x^2 + y^2 = \sqrt{31}$
$\displaystyle x^2 + y^2 = 31$
$\displaystyle x^2 + y^2 = 5$
None of the above

(d) What is the area of the cross-section $z = 5$ of the pile?

(e) What is $A(z)\text{,}$ the area of a horizontal cross-section at height $z\text{?}$

$A(z) =$ square meters

(f) Use your answer in part (e) to find the volume of the pile.

Volume = cubic meters

Answer. 1

Answer. 2

$113.097$

Answer. 3

Answer. 4

$31\pi $

10.

Match the following integrals with the verbal descriptions of the solids whose volumes they give. Put the letter of the verbal description to the left of the corresponding integral.

$\displaystyle \displaystyle \int_{0}^{\frac{1}{\sqrt{3}}}\!\!\int_{0}^{\frac{1}{2}\sqrt{1-3y^{2}}} \sqrt{1 -4x^{2} - 3y^{2}} \: dx dy$
$\displaystyle \displaystyle \int_{0}^{1}\!\!\int_{y^{2}}^{\sqrt{y}} 4x^{2} + 3y^{2} \: dx dy$
$\displaystyle \displaystyle \int_{-1}^{1}\!\!\int_{-\sqrt{1-x^{2}}}^{\sqrt{1-x^{2}}} 1 - x^{2} - y^{2}\: dy dx$
$\displaystyle \displaystyle \int_{0}^{2}\!\!\int_{-2}^{2} \sqrt{4 - y^{2}} \: dy dx$
$\displaystyle \displaystyle \int_{-2}^{2}\!\!\int_{4}^{4 + \sqrt{4-x^{2}}} 4x + 3y \: dy dx$

Solid under an elliptic paraboloid and over a planar region bounded by two parabolas.
Solid under a plane and over one half of a circular disk.
One half of a cylindrical rod.
One eighth of an ellipsoid.
Solid bounded by a circular paraboloid and a plane.

11.

For each of the following iterated integrals,

sketch the region of integration,
write an equivalent iterated integral expression in the opposite order of integration,
choose one of the two orders and evaluate the integral.

$\displaystyle \int_{x=0}^{x=1} \int_{y=x^2}^{y=x} xy \, dy \, dx$
$\displaystyle \int_{y=0}^{y=2} \int_{x=-\sqrt{4-y^2}}^{x=0} xy \, dx \, dy$
$\displaystyle \int_{x=0}^{x=1} \int_{y=x^4}^{y=x^{1/4}} x+y \, dy \, dx$
$\displaystyle \int_{y=0}^{y=2} \int_{x=y/2}^{x=2y} x+y \, dx \, dy$

12.

The temperature at any point on a metal plate in the $xy$-plane is given by $T(x,y) = 100-4x^2 - y^2\text{,}$ where $x$ and $y$ are measured in inches and $T$ in degrees Celsius. Consider the portion of the plate that lies on the region $D$ that is the finite region that lies between the parabolas $x = y^2$ and $x = 3 - 2y^2\text{.}$

Construct a labeled sketch of the region $D\text{.}$
Set up an iterated integral whose value is $\iint_D T(x,y) \, dA\text{,}$ using $dA = dx dy\text{.}$ (Hint: It is possible that more than one integral is needed.)
Set up an integrated integral whose value is $\iint_D T(x,y) \, dA\text{,}$ using $dA = dy dx\text{.}$ (Hint: It is possible that more than one integral is needed.)
Use the Fundamental Theorem of Calculus to evaluate the integrals you determined in (b) and (c).
Determine the exact average temperature, $T_{\operatorname{AVG}(D)}\text{,}$ over the region $D\text{.}$

13.

Consider the solid that is given by the following description: the base is the given region $D\text{,}$ while the top is given by the surface $z = p(x,y)\text{.}$ In each setting below, set up, but do not evaluate, an iterated integral whose value is the exact volume of the solid. Include a labeled sketch of $D$ in each case.

$D$ is the interior of the quarter circle of radius 2, centered at the origin, that lies in the second quadrant of the plane; $p(x,y) = 16-x^2-y^2\text{.}$
$D$ is the finite region between the line $y = x + 1$ and the parabola $y = x^2\text{;}$ $p(x,y) = 10-x-2y\text{.}$
$D$ is the triangular region with vertices $(1,1)\text{,}$ $(2,2)\text{,}$ and $(2,3)\text{;}$ $p(x,y) = e^{-xy}\text{.}$
$D$ is the region bounded by the $y$-axis, $y = 4$ and $x = \sqrt{y}\text{;}$ $p(x,y) = \sqrt{1 + x^2 + y^2}\text{.}$

14.

Consider the iterated integral $\displaystyle I = \int_{x=0}^{x=4} \int_{y=\sqrt{x}}^{y=2} \cos(y^3) \, dy \, dx\text{.}$

Sketch the region of integration.
Write an equivalent iterated integral with the order of integration reversed.
Choose one of the two orders of integration and evaluate the iterated integral you chose by hand. Explain the reasoning behind your choice.
Determine the exact average value of $\cos(y^3)$ over the region $D$ that is determined by the iterated integral $I\text{.}$

11.4: Applications of Double Integrals

1.

The masses $m_i$ are located at the points $P_i\text{.}$ Find the center of mass of the system.

$m_1=1\text{,}$ $m_2=8\text{,}$ $m_3=6\text{.}$

$P_1=(1,-4)\text{,}$ $P_2=(-6,7)\text{,}$ $P_3=(9,-7)\text{.}$

$\bar x$=

$\bar y$=

Answer. 1

$0.466666666666667$

Answer. 2

$0.666666666666667$

2.

Find the centroid $(\bar x,\bar y)$ of the triangle with vertices at $(0,0)\text{,}$ $(5,0)\text{,}$ and $(0,2)\text{.}$

$\bar x$=

$\bar y$=

Answer. 1

$1.66666666666667$

Answer. 2

$0.666666666666667$

3.

Find the mass of the rectangular region $0 \leq x \leq 2\text{,}$ $0 \leq y \leq 1$ with density function $\rho \left( x, y \right) = 1 - y\text{.}$

Answer.

$1$

4.

Find the mass of the triangular region with vertices (0, 0), (3, 0), and (0, 5), with density function $\rho \left( x, y \right) = x^2 + y^2\text{.}$

Answer.

$42.5$

5.

A lamina occupies the region inside the circle $x^2 + y^2 = 8 y$ but outside the circle $x^2 + y^2 = 16\text{.}$ The density at each point is inversely proportional to its distance from the orgin.

Where is the center of mass?

( , )

Answer. 1

$0$

Answer. 2

$5.05816623182515$

6.

A sprinkler distributes water in a circular pattern, supplying water to a depth of $e^{-r}$ feet per hour at a distance of r feet from the sprinkler.

A. What is the total amount of water supplied per hour inside of a circle of radius 6?

${ft}^3$ per hour

B. What is the total amount of water that goes through the sprinkler per hour?

${ft}^3$ per hour

Answer. 1

$6.1741640923836$

Answer. 2

$6.28318530717959$

7.

Let $p$ be the joint density function such that $p(x,y) = \frac{1}{144} xy$ in $R\text{,}$ the rectangle $0 \le x \le 6, 0\le y \le 4\text{,}$ and $p(x,y)=0$ outside $R\text{.}$ Find the fraction of the population satisfying the constraint $x+y \le 10$

fraction =

Answer.

$1$

8.

A lamp has two bulbs, each of a type with an average lifetime of 10 hours. The probability density function for the lifetime of a bulb is $f(t) = \frac{1}{10} e^{-t/10}, t \geq 0\text{.}$

What is the probability that both of the bulbs will fail within 3 hours?

Answer.

$0.0671751947305907$

9.

For the following two functions $p(x,y)\text{,}$ check whether $p$ is a joint density function. Assume $p(x,y)=0$ outside the region $R\text{.}$

(a) $p(x,y)=3\text{,}$ where $R$ is $-1 \le x \le 1, 0 \le y \le 0.5\text{.}$

$p(x,y)$

is a joint density function
is not a joint density function

(b) $p(x,y)=1\text{,}$ where $R$ is $1 \le x \le 1.5, 0 \le y \le 2\text{.}$

$p(x,y)$

is a joint density function
is not a joint density function

Then, for the region $R$ given by $-1 \le x \le 3, 0 \le y \le 3\text{,}$ what constant function $p(x,y)$ is a joint density function?

$p(x,y) =$

Answer. 1

$\text{is not a joint density function}$

Answer. 2

$\text{is a joint density function}$

Answer. 3

$\frac{1}{4\cdot 3}$

10.

Let $x$ and $y$ have joint density function

\[ p(x,y) = \begin{cases} {2 \over 3}(x + 2y)\quad& \mbox{for } 0 \le x \le 1, 0 \le y \le 1,\\[4pt] 0 & \mbox{otherwise.} \end{cases} \nonumber \]

Find the probability that

(a) $x > 1/2\text{:}$

probability =

(b) $x \lt \frac{1}{2} + y\text{:}$

probability =

Answer. 1

$1-\frac{2}{3\cdot 2}-\frac{1}{3\cdot 2\cdot 2}$

Answer. 2

$1-\left(\frac{4}{9}-\frac{1}{2}+\frac{2}{3\cdot 2\cdot 2}-\frac{1}{9\cdot 2^{3}}\right)$

11.

A triangular plate is bounded by the graphs of the equations $y = 2x\text{,}$ $y = 4x\text{,}$ and $y = 4\text{.}$ The plate's density at $(x,y)$ is given by $\delta(x,y) = 4xy^2 + 1\text{,}$ measured in grams per square centimeter (and $x$ and $y$ are measured in centimeters).

Set up an iterated integral whose value is the mass of the plate. Include a labeled sketch of the region of integration. Why did you choose the order of integration you did?
Determine the mass of the plate.
Determine the exact center of mass of the plate. Draw and label the point you find on your sketch from (a).
What is the average density of the plate? Include units on your answer.

12.

Let $D$ be a half-disk lamina of radius 3 in quadrants IV and I, centered at the origin as in Activity 11.4.2. Assume the density at point $(x,y)$ is equal to $x\text{.}$

Before doing any calculations, what do you expect the $y$-coordinate of the center of mass to be? Why?
Set up iterated integral expressions which, if evaluated, will determine the exact center of mass of the lamina.
Use appropriate technology to evaluate the integrals to find the center of mass numerically.

13.

Let $x$ denote the time (in minutes) that a person spends waiting in a checkout line at a grocery store and $y$ the time (in minutes) that it takes to check out. Suppose the joint probability density for $x$ and $y$ is

\[ f(x,y) = \frac{1}{8} e^{-x/4-y/2}. \nonumber \]

What is the exact probability that a person spends between 0 to 5 minutes waiting in line, and then 0 to 5 minutes waiting to check out?
Set up, but do not evaluate, an iterated integral whose value determines the exact probability that a person spends at most 10 minutes total both waiting in line and checking out at this grocery store.
Set up, but do not evaluate, an iterated integral expression whose value determines the exact probability that a person spends at least 10 minutes total both waiting in line and checking out, but not more than 20 minutes.

11.5: Double Integrals in Polar Coordinates

1.

For each set of Polar coordinates, match the equivalent Cartesian coordinates.

2.

(a) The Cartesian coordinates of a point are $(-1,-\sqrt{3}).$

(i) Find polar coordinates $(r,\theta)$ of the point, where $r>0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

(ii) Find polar coordinates $(r,\theta)$ of the point, where $r\lt 0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

(b) The Cartesian coordinates of a point are $(-2,3).$

(i) Find polar coordinates $(r,\theta)$ of the point, where $r>0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

(ii) Find polar coordinates $(r,\theta)$ of the point, where $r\lt 0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

Answer. 1

$2$

Answer. 2

$4.18879020478639$

Answer. 3

$-2$

Answer. 4

$1.0471975511966$

Answer. 5

$3.60555127546399$

Answer. 6

$2.15879893034246$

Answer. 7

$-3.60555127546399$

Answer. 8

$5.30039158393226$

3.

(a) You are given the point $(1,\pi/2)$ in polar coordinates.

(i) Find another pair of polar coordinates for this point such that $r > 0$ and $2\pi \le \theta \lt 4\pi.$

$r =$

$\theta =$

(ii) Find another pair of polar coordinates for this point such that $r \lt 0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

(b) You are given the point $(-2,\pi/4)$ in polar coordinates.

(i) Find another pair of polar coordinates for this point such that $r > 0$ and $2\pi \le \theta \lt 4\pi.$

$r =$

$\theta =$

(ii) Find another pair of polar coordinates for this point such that $r \lt 0$ and $-2\pi \le \theta \lt 0.$

$r =$

$\theta =$

(i) Find another pair of polar coordinates for this point such that $r > 0$ and $2\pi \le \theta \lt 4\pi.$

$r =$

$\theta =$

(ii) Find another pair of polar coordinates for this point such that $r \lt 0$ and $0 \le \theta \lt 2\pi.$

$r =$

$\theta =$

Answer. 1

$1$

Answer. 2

$7.85398163397448$

Answer. 3

$-1$

Answer. 4

$4.71238898038469$

Answer. 5

$2$

Answer. 6

$10.2101761241668$

Answer. 7

$-2$

Answer. 8

$-5.49778714378214$

Answer. 9

$3$

Answer. 10

$8.28318530717959$

Answer. 11

$-3$

Answer. 12

$5.14159265358979$

4.

Decide if the points given in polar coordinates are the same. If they are the same, enter T . If they are different, enter F .

a.) $(5, \frac{\pi}{3}), (-5, \frac{-\pi}{3})$

b.) $(2, \frac{35 \pi}{4}), (2,- \frac{35 \pi}{4})$

c.) $(0, 5 \pi), (0, \frac{4 \pi}{4})$

d.) $(1, \frac{141 \pi}{4}), (-1, \frac{\pi}{4})$

e.) $(2, \frac{92 \pi}{3}), (-2, \frac{- \pi}{3})$

f.)$(5,15 \pi), (-5, 15 \pi)$

Answer. 1

Answer. 2

Answer. 3

Answer. 4

Answer. 5

Answer. 6

5.

A curve with polar equation

\[ r=\frac{17 }{7 \sin \theta+57 \cos \theta} \nonumber \]

represents a line. Write this line in the given Cartesian form.

$y =$

Note: Your answer should be a function of $x$.

Answer.

$2.42857-8.14286x$

6.

Find a polar equation of the form $r=f(\theta)$ for the curve represented by the Cartesian equation $x=-y^2.$

Note: Since $\theta$ is not a symbol on your keyboard, use $t$ in place of $\theta$ in your answer.

$r =$

Answer.

$\frac{\frac{-1\cos\!\left(t\right)}{\sin\!\left(t\right)}}{\sin\!\left(t\right)}$

7.

By changing to polar coordinates, evaluate the integral

\[ \iint_D (x^2 + y^2)^{3/2}\, dx dy \nonumber \]

where $D$ is the disk $x^2 + y^2 \le 36\text{.}$

Answer =

Answer.

$9771.60978972569$

8.

Convert the integral

\[ \int_0^{\sqrt{10}}\int_{-x}^x\,dy\,dx \nonumber \]

to polar coordinates and evaluate it (use $t$ for $\theta$):

With $a =$, $b =$, $c =$ and $d =$,

$\int_0^{\sqrt{10}}\int_{-x}^x\,dy\,dx = \int_{a}^{b}\int_{c}^{d}$ $dr\,dt$

$= \int_{a}^{b}$ $\,dt$

$=$ $\bigg|_{a}^{b}$

$=$.

Answer. 1

$\frac{-\pi }{4}$

Answer. 2

$\frac{\pi }{4}$

Answer. 3

$0$

Answer. 4

$\frac{\sqrt{10}}{\cos\!\left(t\right)}$

Answer. 5

$r$

Answer. 6

$\frac{5}{\cos^{2}\!\left(t\right)}$

Answer. 7

$5\tan\!\left(t\right)$

Answer. 8

$10$

9.

For each of the following, set up the integral of an arbitrary function $f(x,y)$ over the region in whichever of rectangular or polar coordinates is most appropriate. (Use $t$ for $\theta$ in your expressions.)

(a) The region

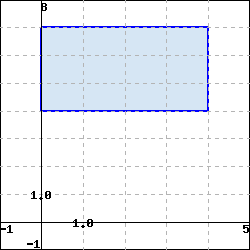
$webwork-226-image-1.png$

With $a =$, $b =$,

$c =$, and $d =$,

integral = $\int_a^b \int_c^d$ $d$ $d$

(b) The region

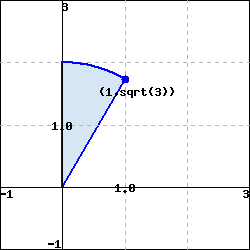
$webwork-226-image-2.png$

With $a =$, $b =$,

$c =$, and $d =$,

integral = $\int_a^b \int_c^d$ $d$ $d$

Answer. 1

$0$

Answer. 2

$4$

Answer. 3

$4$

Answer. 4

$7$

Answer. 5

$f\!\left(x,y\right)$

Answer. 6

$y$

Answer. 7

$x$

Answer. 8

$1.0472$

Answer. 9

$1.5708$

Answer. 10

$0$

Answer. 11

$2$

Answer. 12

$rf\!\left(r\cos\!\left(t\right),r\sin\!\left(t\right)\right)$

Answer. 13

$r$

Answer. 14

$t$

10.

A Cartesian equation for the polar equation $r=3$ can be written as:

$x^2+y^2 =$

Answer.

$9$

11.

Using polar coordinates, evaluate the integral which gives the area which lies in the first quadrant between the circles $x^2 + y^2 = 36$ and $x^2 - 6x + y^2 = 0\text{.}$

Answer.

$14.1371669411541$

12.

(a) Graph $r=1/(4\cos\theta)$ for $-\pi/2\le\theta\le\pi/2$ and $r=1\text{.}$ Then write an iterated integral in polar coordinates representing the area inside the curve $r=1$ and to the right of $r=1/(4\cos\theta)\text{.}$ (Use $t$ for $\theta$ in your work.)

With $a =$, $b =$,

$c =$, and $d =$,

area = $\int_a^b\int_c^d\,$$d$ $d$

(b) Evaluate your integral to find the area.

area =

Answer. 1

$-\cos^{-1}\!\left(\frac{1}{4}\right)$

Answer. 2

$\cos^{-1}\!\left(\frac{1}{4}\right)$

Answer. 3

$\frac{1}{4\cos\!\left(t\right)}$

Answer. 4

$1$

Answer. 5

$r$

Answer. 6

$r$

Answer. 7

$t$

Answer. 8

$\cos^{-1}\!\left(\frac{1}{4}\right)-\frac{\tan\!\left(\cos^{-1}\!\left(\frac{1}{4}\right)\right)}{4^{2}}$

13.

Using polar coordinates, evaluate the integral $\displaystyle \int \!\! \int_{R} \sin (x^2+y^2) dA$ where R is the region $4 \leq x^2 + y^2 \leq 25\text{.}$

Answer.

$-5.16743746933879$

14.

Sketch the region of integration for the following integral.

$\displaystyle \int_{0}^{\pi/4} \int_{0}^{5 / \cos(\theta)} f(r,\theta) \, r \, dr \, d\theta$

The region of integration is bounded by

$\displaystyle y = 0, y = x, \mbox{ and } y = 5$
$\displaystyle y = 0, x = \sqrt{25 - y^2}, \mbox{ and } y = 5$
$\displaystyle y = 0, y = \sqrt{25 - x^2}, \mbox{ and } x = 5$
$\displaystyle y = 0, y = x, \mbox{ and } x = 5$
None of the above

15.

Use the polar coordinates to find the volume of a sphere of radius 7.

Answer.

$1436.75504024173$

16.

Consider the solid under the graph of $z = e^{-x^2-y^2}$ above the disk $x^2 + y^2 \leq a^2\text{,}$ where $a > 0\text{.}$

(a) Set up the integral to find the volume of the solid.

Instructions: Please enter the integrand in the first answer box, typing theta for $\theta\text{.}$ Depending on the order of integration you choose, enter dr and dtheta in either order into the second and third answer boxes with only one dr or dtheta in each box. Then, enter the limits of integration.

$\displaystyle \int_A^B \int_C^D$

A =

B =

C =

D =

(b) Evaluate the integral and find the volume. Your answer will be in terms of $a\text{.}$

Volume V =

$\displaystyle \lim_{a \to \infty} V =$

Answer. 1

$e^{-r^{2}}r;\,dr;\,dtheta;\,0;\,2\pi ;\,0;\,a$

Answer. 2

$\pi \!\left(1-e^{-a^{2}}\right)$

Answer. 3

$3.14159$

17.

Consider the iterated integral $I = \int_{-3}^{0} \int_{-\sqrt{9-y^2}}^{0} \frac{y}{x^2 + y^2+1} \, dx \, dy.$

Sketch (and label) the region of integration.
Convert the given iterated integral to one in polar coordinates.
Evaluate the iterated integral in (b).
State one possible interpretation of the value you found in (c).

18.

Let $D$ be the region that lies inside the unit circle in the plane.

Set up and evaluate an iterated integral in polar coordinates whose value is the area of $D\text{.}$
Determine the exact average value of $f(x,y) = y$ over the upper half of $D\text{.}$
Find the exact center of mass of the lamina over the portion of $D$ that lies in the first quadrant and has its mass density distribution given by $\delta(x,y) = 1\text{.}$ (Before making any calculations, where do you expect the center of mass to lie? Why?)
Find the exact volume of the solid that lies under the surface $z = 8-x^2-y^2$ and over the unit disk, $D\text{.}$

19.

For each of the following iterated integrals,

sketch and label the region of integration,
convert the integral to the other coordinate system (if given in polar, to rectangular; if given in rectangular, to polar), and
choose one of the two iterated integrals to evaluate exactly.

$\displaystyle \int_{\pi}^{3\pi/2} \int_{0}^{3} r^3 \, dr \, d\theta$
$\displaystyle \int_{0}^{2} \int_{-\sqrt{1-(x-1)^2}}^{\sqrt{1-(x-1)^2}} \sqrt{x^2 + y^2} \, dy \, dx$
$\displaystyle \int_0^{\pi/2} \int_0^{\sin(\theta)} r \sqrt{1-r^2} \, dr \, d\theta.$
$\displaystyle \int_0^{\sqrt{2}/2} \int_y^{\sqrt{1-y^2}} \cos(x^2 + y^2) \, dx \, dy.$

11.6: Surfaces Defined Parametrically and Surface Area

1.

Consider the cone shown below.

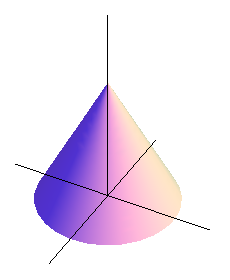
$webwork-236-image-1.png$

If the height of the cone is 8 and the base radius is 9, write a parameterization of the cone in terms of $r = s$ and $\theta = t\text{.}$

$x(s,t) =$,

$y(s,t) =$, and

$z(s,t) =$, with

$\le s\le$ and

$\le t\le$.

Answer. 1

$s\cos\!\left(t\right)$

Answer. 2

$s\sin\!\left(t\right)$

Answer. 3

$8-\frac{8}{9}s$

Answer. 4

$0$

Answer. 5

$9$

Answer. 6

$0$

Answer. 7

$2\pi $

2.

Parameterize the plane through the point $(-5, -1, 3)$ with the normal vector $\left\lt -5,4,2\right>$

$\vec r(s,t) =$

(Use $s$ and $t$ for the parameters in your parameterization, and enter your vector as a single vector, with angle brackets: e.g., as \lt 1 + s + t, s - t, 3 - t \gt.)

Answer.

$\left<-\left(5+4s+2t\right),-\left(1+5s\right),3-5t\right>$

3.

Parameterize a vase formed by rotating the curve $z= 2 \sqrt{x-1},\,1\leq x\leq 2\text{,}$ around the $z$-axis. Use $s$ and $t$ for your parameters.

$x(s,t) =$,

$y(s,t) =$, and

$z(s,t) =$, with

$\le s\le$ and

$\le t\le$

Answer. 1

$s\cos\!\left(t\right)$

Answer. 2

$s\sin\!\left(t\right)$

Answer. 3

$2\sqrt{s-1}$

Answer. 4

$1$

Answer. 5

$2$

Answer. 6

$0$

Answer. 7

$2\pi $

4.

Find parametric equations for the sphere centered at the origin and with radius 4. Use the parameters $s$ and $t$ in your answer.

$x(s,t) =$,

$y(s,t) =$, and

$z(s,t) =$, where

$\le s\le$ and

$\le t\le$.

Answer. 1

$4\cos\!\left(t\right)\sin\!\left(s\right)$

Answer. 2

$4\sin\!\left(t\right)\sin\!\left(s\right)$

Answer. 3

$4\cos\!\left(s\right)$

Answer. 4

$0$

Answer. 5

$2\pi $

Answer. 6

$0$

Answer. 7

$\pi $

5.

Find the surface area of that part of the plane $5 x + 10 y + z = 3$ that lies inside the elliptic cylinder $\frac{x^2}{16} + \frac{y^2}{81} =1$

Surface Area =

Answer.

$1269.51444272221$

6.

Find the surface area of the part of the circular paraboloid $z = x^{2} + y^{2}$ that lies inside the cylinder $x^{2} + y^{2} = 9\text{.}$

Answer.

$117.318700709818$

7.

Find the surface area of the part of the plane $3 x + 4 y + z = 5$ that lies inside the cylinder $x^{2} + y^{2} = 16\text{.}$

Answer.

$256.304675910625$

8.

Write down the iterated integral which expresses the surface area of $z = y^{6}\cos^{4}x$ over the triangle with vertices (-1,1), (1,1), (0,2):

\[ \int_a^b\int_{f(y)}^{g(y)} \sqrt{h(x,y)}\,dx dy \nonumber \]

$a =$

$b =$

$f(y) =$

$g(y) =$

$h(x,y) =$

Answer. 1

$1$

Answer. 2

$2$

Answer. 3

$y-2$

Answer. 4

$2-y$

Answer. 5

$1+y^{12}\cdot 16\cos^{6}\!\left(x\right)\sin^{2}\!\left(x\right)+36y^{10}\cos^{8}\!\left(x\right)$

9.

A decorative oak post is 60 inches long and is turned on a lathe so that its profile is sinusoidal as shown in the figure below.

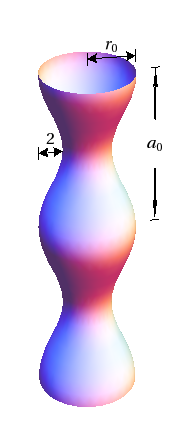
$webwork-244-image-1.png$

In this figure, $r_0 = 6$ inches and $a_0 = 12$ inches.

(a) Describe the surface of the post parametrically using cylindrical coordinates and the parameters $s$ and $t\text{.}$

$x(s,t) =$,

$y(s,t) =$, and

$z(s,t) =$, where

$\le s\le$ and

$\le t\le$.

(b) Find the volume of the post.

volume =

(Include units.)

Answer. 1

$\left(5+\cos\!\left(\frac{\pi s}{6}\right)\right)\cos\!\left(t\right)$

Answer. 2

$\left(5+\cos\!\left(\frac{\pi s}{6}\right)\right)\sin\!\left(t\right)$

Answer. 3

$s$

Answer. 4

$0$

Answer. 5

$60$

Answer. 6

$0$

Answer. 7

$2\pi $

Answer. 8

$4806.64\ {\rm in^{3}}$

10.

Consider the ellipsoid given by the equation

\[ \frac{x^2}{16} + \frac{y^2}{25} + \frac{z^2}{9} = 1. \nonumber \]

In Activity 11.6.2, we found that a parameterization of the sphere $S$ of radius $R$ centered at the origin is

\[ x(r,s) = R\cos(s) \cos(t), \ y(s,t) = R \cos(s) \sin(t), \ \text{ and } \ z(s,t) = R\sin(s) \nonumber \]

for $-\frac{\pi}{2} \leq s \leq \frac{\pi}{2}$ and $0 \leq t \leq 2\pi\text{.}$

Let $(x,y,z)$ be a point on the ellipsoid and let $X = \frac{x}{4}\text{,}$ $Y = \frac{y}{5}\text{,}$ and $Z = \frac{z}{3}\text{.}$ Show that $(X,Y,Z)$ lies on the sphere $S\text{.}$ Hence, find a parameterization of $S$ in terms of $X\text{,}$ $Y\text{,}$ and $Z$ as functions of $s$ and $t\text{.}$
Use the result of part (a) to find a parameterization of the ellipse in terms of $x\text{,}$ $y\text{,}$ and $z$ as functions of $s$ and $t\text{.}$ Check your parametrization by substituting $x\text{,}$ $y\text{,}$ and $z$ into the equation of the ellipsoid. Then check your work by plotting the surface defined by your parameterization.

11.

In this exercise, we explore how to use a parametrization and iterated integral to determine the surface area of a sphere.

Set up an iterated integral whose value is the portion of the surface area of a sphere of radius $R$ that lies in the first octant (see the parameterization you developed in Activity 11.6.2).
Then, evaluate the integral to calculate the surface area of this portion of the sphere.
By what constant must you multiply the value determined in (b) in order to find the total surface area of the entire sphere.
Finally, compare your result to the standard formula for the surface area of sphere.

12.

Consider the plane generated by $z = f(x,y) = 24 - 2x - 3y$ over the region $D = [0,2]\times[0,3]\text{.}$

Sketch a picture of the overall solid generated by the plane over the given domain.
Determine a parameterization $\mathbf{r}(s,t)$ for the plane over the domain $D\text{.}$
Use Equation (11.6.2) to determine the surface area generated by $f$ over the domain $D\text{.}$
Observe that the vector $\mathbf{u} = \langle 2, 0, -4 \rangle$ points from $(0,0,24)$ to $(2,0,20)$ along one side of the surface generated by the plane $f$ over $D\text{.}$ Find the vector $\mathbf{v}$ such that $\mathbf{u}$ and $\mathbf{v}$ together span the parallelogram that represents the surface defined by $f$ over $D\text{,}$ and hence compute $| \mathbf{u} \times \mathbf{v} |\text{.}$ What do you observe about the value you find?

13.

A cone with base radius $a$ and height $h$ can be realized as the surface defined by $z = \frac{h}{a} \sqrt{x^2+y^2}\text{,}$ where $a$ and $h$ are positive.

Find a parameterization of the cone described by $z = \frac{h}{a} \sqrt{x^2+y^2}\text{.}$ (Hint: Compare to the parameterization of a cylinder as seen in Activity 11.6.3.)
Set up an iterated integral to determine the surface area of this cone.
Evaluate the iterated integral to find a formula for the lateral surface area of a cone of height $h$ and base $a\text{.}$

11.7: Triple Integrals

Exercises 11.7.3 Exercises

1.

Find the triple integral of the function $f(x,y,z) = x^{2}\cos\!\left(y+z\right)$ over the cube $6 \leq x \leq 8\text{,}$ $0 \leq y \leq \pi\text{,}$ $0 \leq z \leq \pi.$

Answer.

$-394.667$

2.

Evaluate the triple integral

\[ \int \!\! \int \!\! \int_{\mathbf{E}} xyz \, dV \nonumber \]

where E is the solid: $0 \leq z \leq 1 , \ \ 0 \leq y \leq z, \ \ 0 \leq x \leq y\text{.}$

Answer.

$0.0208333333333333$

3.

Find the mass of the rectangular prism $0 \leq x \leq 1, \ \ 0 \leq y \leq 4, \ \ 0 \leq z \leq 4\text{,}$ with density function $\rho \left( x, y, z \right) = x\text{.}$

Answer.

$8$

4.

Find the average value of the function $f \left( x, y, z \right) = y e^{-xy}$ over the rectangular prism $0 \leq x \leq 2\text{,}$ $0 \leq y \leq 3\text{,}$ $0 \leq z \leq 2$

Answer.

$0.416873229348056$

5.

Find the volume of the solid bounded by the planes x = 0, y = 0, z = 0, and x + y + z = 4.

Answer.

$10.6666666666667$

6.

Find the mass of the solid bounded by the $xy$-plane, $yz$-plane, $xz$-plane, and the plane $(x/3)+(y/4)+(z/12) = 1\text{,}$ if the density of the solid is given by $\delta (x,y,z)=x + 2 y\text{.}$

mass =

Answer.

$\frac{3\cdot 3\cdot 4\cdot 4\cdot \left(3+4\cdot 2\right)}{24}$

7.

The moment of inertia of a solid body about an axis in 3-space relates the angular acceleration about this axis to torque (force twisting the body). The moments of inertia about the coordinate axes of a body of constant density and mass $m$ occupying a region $W$ of volume $V$ are defined to be

\[ I_x = \frac{m}{V}\int_W (y^2+z^2) \,dV\qquad I_y = \frac{m}{V}\int_W (x^2+z^2) \,dV\qquad I_z = \frac{m}{V}\int_W (x^2+y^2) \,dV \nonumber \]

Use these definitions to find the moment of inertia about the $z$-axis of the rectangular solid of mass $27$ given by $0 \le x \le 3\text{,}$ $0 \le y \le 3\text{,}$ $0 \le z \le 3\text{.}$

$I_x =$

$I_y =$

$I_z =$

Answer. 1

$\frac{1\cdot 3\cdot 3\cdot 3\cdot \left(3\cdot 3+3\cdot 3\right)}{3}$

Answer. 2

$\frac{1\cdot 3\cdot 3\cdot 3\cdot \left(3\cdot 3+3\cdot 3\right)}{3}$

Answer. 3

$\frac{1\cdot 3\cdot 3\cdot 3\cdot \left(3\cdot 3+3\cdot 3\right)}{3}$

8.

Express the integral $\displaystyle \iiint_E f(x,y,z) dV$ as an iterated integral in six different ways, where E is the solid bounded by $z =0, x = 0, z = y - 6 x$ and $y = 12\text{.}$

1. $\displaystyle \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{h_1(x,y)}^{h_2(x,y)}f(x,y,z) dz dy dx$

$a =$ $b =$

$g_1(x) =$ $g_2(x) =$

$h_1(x,y) =$ $h_2(x,y) =$

2. $\displaystyle \int_a^b \int_{g_1(y)}^{g_2(y)} \int_{h_1(x,y)}^{h_2(x,y)}f(x,y,z) dz dx dy$

$a =$ $b =$

$g_1(y) =$ $g_2(y) =$

$h_1(x,y) =$ $h_2(x,y) =$

3. $\displaystyle \int_a^b \int_{g_1(z)}^{g_2(z)} \int_{h_1(y,z)}^{h_2(y,z)}f(x,y,z) dx dy dz$

$a =$ $b =$

$g_1(z) =$ $g_2(z) =$

$h_1(y,z) =$ $h_2(y,z) =$

4. $\displaystyle \int_a^b \int_{g_1(y)}^{g_2(y)} \int_{h_1(y,z)}^{h_2(y,z)}f(x,y,z) dx dz dy$

$a =$ $b =$

$g_1(y) =$ $g_2(y) =$

$h_1(y,z) =$ $h_2(y,z) =$

5. $\displaystyle \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{h_1(x,z)}^{h_2(x,z)}f(x,y,z) dy dz dx$

$a =$ $b =$

$g_1(x) =$ $g_2(x) =$

$h_1(x,z) =$ $h_2(x,z) =$

6. $\displaystyle \int_a^b \int_{g_1(z)}^{g_2(z)} \int_{h_1(x,z)}^{h_2(x,z)}f(x,y,z) dy dx dz$

$a =$ $b =$

$g_1(z) =$ $g_2(z) =$

$h_1(x,z) =$ $h_2(x,z) =$

Answer. 1

$0$

Answer. 2

$2$

Answer. 3

$6x$

Answer. 4

$12$

Answer. 5

$0$

Answer. 6

$y-6x$

Answer. 7

$0$

Answer. 8

$12$

Answer. 9

$0$

Answer. 10

$\frac{y}{6}$

Answer. 11

$0$

Answer. 12

$y-6x$

Answer. 13

$0$

Answer. 14

$12$

Answer. 15

$z$

Answer. 16

$12$

Answer. 17

$0$

Answer. 18

$\frac{y-z}{6}$

Answer. 19

$0$

Answer. 20

$12$

Answer. 21

$0$

Answer. 22

$y$

Answer. 23

$0$

Answer. 24

$\frac{y-z}{6}$

Answer. 25

$0$

Answer. 26

$2$

Answer. 27

$0$

Answer. 28

$12-6x$

Answer. 29

$6x+z$

Answer. 30

$12$

Answer. 31

$0$

Answer. 32

$12$

Answer. 33

$0$

Answer. 34

$2-\frac{z}{6}$

Answer. 35

$6x+z$

Answer. 36

$12$

9.

Calculate the volume under the elliptic paraboloid $z = 4x^2 + 8y^2$ and over the rectangle $R = [-2, 2] \times [-3, 3]\text{.}$

Answer.

$704$

10.

The motion of a solid object can be analyzed by thinking of the mass as concentrated at a single point, the center of mass. If the object has density $\rho(x,y,z)$ at the point $(x,y,z)$ and occupies a region $W\text{,}$ then the coordinates $(\overline{x},\overline{y},\overline{z})$ of the center of mass are given by

\[ \overline{x} = \frac{1}{m}\int_W x\rho \, dV \quad \overline{y} = \frac{1}{m}\int_W y\rho \, dV \quad \overline{z} = \frac{1}{m}\int_W z\rho \, dV, \nonumber \]

Assume $x\text{,}$ $y\text{,}$ $z$ are in cm. Let $C$ be a solid cone with both height and radius 5 and contained between the surfaces $z=\sqrt{x^2+y^2}$ and $z=5\text{.}$ If $C$ has constant mass density of 3 g/cm$^3\text{,}$ find the $z$-coordinate of $C$'s center of mass.

$\overline z =$

(Include units.)

Answer.

$3.75\ {\rm cm}$

11.

Without calculation, decide if each of the integrals below are positive, negative, or zero. Let W be the solid bounded by $z = \sqrt{x^2 + y^2}$ and $z = 2\text{.}$

$\displaystyle \displaystyle \iiint\limits_W \left( z - \sqrt{x^2+y^2} \right) \, dV$
$\displaystyle \displaystyle \iiint\limits_W \left( z - 2 \right) \, dV$
$\displaystyle \displaystyle \iiint\limits_W e^{-xyz} \, dV$

12.

Set up a triple integral to find the mass of the solid tetrahedron bounded by the xy-plane, the yz-plane, the xz-plane, and the plane $x/3 + y/2 + z/6 = 1\text{,}$ if the density function is given by $\delta(x,y,z) = x + y\text{.}$ Write an iterated integral in the form below to find the mass of the solid.

$\displaystyle \iiint\limits_R f(x,y,z) \, dV = \int_A^B \!\! \int_C^D \!\! \int_E^F$ $\, dz \, dy \, dx$

with limits of integration

A =

B =

C =

D =

E =

F =

Answer. 1

$x+y$

Answer. 2

$0$

Answer. 3

$3$

Answer. 4

$0$

Answer. 5

$2-0.666667x$

Answer. 6

$0$

Answer. 7

$6-2x-3y$

13.

Consider the solid $S$ that is bounded by the parabolic cylinder $y = x^2$ and the planes $z=0$ and $z=1-y$ as shown in Figure 11.7.8.

$fig_11_7_solid.svg$

Figure 11.7.8. The solid bounded by $y = x^2$ and the planes $z=0$ and $z=1-y\text{.}$

Assume the density of $S$ is given by $\delta(x,y,z) = z$

Set up (but do not evaluate) an iterated integral that represents the mass of $S\text{.}$ Integrate first with respect to $z\text{,}$ then $y\text{,}$ then $x\text{.}$ A picture of the projection of $S$ onto the $xy$-plane is shown at left in Figure 11.7.9.
Set up (but do not evaluate) an iterated integral that represents the mass of $S\text{.}$ In this case, integrate first with respect to $y\text{,}$ then $z\text{,}$ then $x\text{.}$ A picture of the projection of $S$ onto the $xz$-plane is shown at center in Figure 11.7.9.
Set up (but do not evaluate) an iterated integral that represents the mass of $S\text{.}$ For this integral, integrate first with respect to $x\text{,}$ then $y\text{,}$ then $z\text{.}$ A picture of the projection of $S$ onto the $yz$-plane is shown at right in Figure 11.7.9.
Which of these three orders of integration is the most natural to you? Why?

$fig_11_7_solid_proj_1.svg$ $fig_11_7_solid_proj_2.svg$ $fig_11_7_solid_proj_3.svg$

Figure 11.7.9. Projections of $S$ onto the $xy\text{,}$ $xz\text{,}$ and $yz$-planes.

14.

This problem asks you to investigate the average value of some different quantities.

Set up, but do not evaluate, an iterated integral expression whose value is the average sum of all real numbers $x\text{,}$ $y\text{,}$ and $z$ that have the following property: $y$ is between 0 and 2, $x$ is greater than or equal to 0 but cannot exceed $2y\text{,}$ and $z$ is greater than or equal to 0 but cannot exceed $x+y\text{.}$
Set up, but do not evaluate, an integral expression whose value represents the average value of $f(x,y,z) = x + y + z$ over the solid region in the first octant bounded by the surface $z = 4 - x - y^2$ and the coordinate planes $x=0\text{,}$ $y=0\text{,}$ $z=0\text{.}$
How are the quantities in (a) and (b) similar? How are they different?

15.

Consider the solid that lies between the paraboloids $z = g(x,y) = x^2 + y^2$ and $z = f(x,y) = 8 - 3x^2 - 3y^2\text{.}$

By eliminating the variable $z\text{,}$ determine the curve of intersection between the two paraboloids, and sketch this curve in the $xy$-plane.
Set up, but do not evaluate, an iterated integral expression whose value determines the mass of the solid, integrating first with respect to $z\text{,}$ then $y\text{,}$ then $x\text{.}$ Assume the the solid's density is given by $\delta(x,y,z) = \frac{1}{x^2 + y^2 + z^2 + 1}\text{.}$
Set up, but do not evaluate, iterated integral expressions whose values determine the mass of the solid using all possible remaining orders of integration. Use $\delta(x,y,z) = \frac{1}{x^2 + y^2 + z^2 + 1}$ as the density of the solid.
Set up, but do not evaluate, iterated integral expressions whose values determine the center of mass of the solid. Again, assume the the solid's density is given by $\delta(x,y,z) = \frac{1}{x^2 + y^2 + z^2 + 1}\text{.}$
Which coordinates of the center of mass can you determine without evaluating any integral expression? Why?

16.

In each of the following problems, your task is to

sketch, by hand, the region over which you integrate
set up iterated integral expressions which, when evaluated, will determine the value sought
use appropriate technology to evaluate each iterated integral expression you develop

Note well: in some problems you may be able to use a double rather than a triple integral, and polar coordinates may be helpful in some cases.

Consider the solid created by the region enclosed by the circular paraboloid $z = 4 - x^2 - y^2$ over the region $R$ in the $xy$-plane enclosed by $y = -x$ and the circle $x^2 + y^2 = 4$ in the first, second, and fourth quadrants. Determine the solid's volume.
Consider the solid region that lies beneath the circular paraboloid $z = 9 - x^2 - y^2$ over the triangular region between $y = x\text{,}$ $y = 2x\text{,}$ and $y = 1\text{.}$ Assuming that the solid has its density at point $(x,y,z)$ given by $\delta(x,y,z) = xyz + 1\text{,}$ measured in grams per cubic cm, determine the center of mass of the solid.
In a certain room in a house, the walls can be thought of as being formed by the lines $y = 0\text{,}$ $y = 12 + x/4\text{,}$ $x = 0\text{,}$ and $x = 12\text{,}$ where length is measured in feet. In addition, the ceiling of the room is vaulted and is determined by the plane $z = 16 - x/6 - y/3\text{.}$ A heater is stationed in the corner of the room at $(0,0,0)$ and causes the temperature in the room at a particular time to be given by
\[ T(x,y,z) = \frac{80}{1 + \frac{x^2}{1000} + \frac{y^2}{1000} + \frac{z^2}{1000}} \nonumber \]
What is the average temperature in the room?
Consider the solid enclosed by the cylinder $x^2 + y^2 = 9$ and the planes $y + z = 5$ and $z = 1\text{.}$ Assuming that the solid's density is given by $\delta(x,y,z) = \sqrt{x^2 + y^2}\text{,}$ find the mass and center of mass of the solid.

11.8: Triple Integrals in Cylindrical and Spherical Coordinates

1.

What are the rectangular coordinates of the point whose cylindrical coordinates are

$(r= 4 ,\ \theta = \frac{2 \pi}{7} ,\ z= -1 )$ ?

Answer. 1

$2.49395920743493$

Answer. 2

$3.12732592987212$

Answer. 3

$-1$

2.

What are the rectangular coordinates of the point whose spherical coordinates are

$\left( 2 , -{\textstyle\frac{2}{3}} \pi, 0 \pi \right)$ ?

$x =$

$y =$

$z =$

Answer. 1

$2\cos\!\left(\frac{-2}{3}\pi \right)\sin\!\left(0\pi \right)$

Answer. 2

$2\sin\!\left(\frac{-2}{3}\pi \right)\sin\!\left(0\pi \right)$

Answer. 3

$2\cos\!\left(0\pi \right)$

3.

What are the cylindrical coordinates of the point whose spherical coordinates are

$(3 ,\ 3 ,\ \frac{5 \pi}{6} )$ ?

$r$ =

$\theta$ =

$z$=

Answer. 1

$1.5$

Answer. 2

$3$

Answer. 3

$-2.59807621135332$

4.

Find an equation for the paraboloid $z = x^{2}+y^{2}$ in spherical coordinates. (Enter rho, phi and theta for $\rho\text{,}$ $\phi$ and $\theta\text{,}$ respectively.)

equation:

Answer.

$rho = \frac{\cos\!\left(phi\right)}{\sin^{2}\!\left(phi\right)}$

5.

Match the given equation with the verbal description of the surface:

Plane
Half plane
Circular Cylinder
Elliptic or Circular Paraboloid
Cone
Sphere

$\displaystyle r =4$
$\displaystyle z = r^2$
$\displaystyle \rho = 2\cos(\phi )$
$\displaystyle \phi = \frac{\pi}{3}$
$\displaystyle r = 2\cos(\theta )$
$\displaystyle r^2 + z^2 =16$
$\displaystyle \rho \cos(\phi )= 4$
$\displaystyle \theta = \frac{\pi}{3}$
$\displaystyle \rho = 4$

6.

Match the integrals with the type of coordinates which make them the easiest to do. Put the letter of the coordinate system to the left of the number of the integral.

$\displaystyle \int \!\! \int \!\! \int_E \ z \ dV$ where E is: $1 \leq x \leq 2, \ \ 3 \leq y \leq 4, \ \ 5 \leq z \leq 6$
$\displaystyle \displaystyle \int_{0}^{1} \! \int^{y^2}_{0} \ \frac{1}{x} \ dx \ dy$
$\displaystyle \int \!\! \int \!\! \int_E \ z^2 \ dV$ where E is: $-2 \leq z \leq 2, \ \ 1 \leq x^2+y^2 \leq 2$
$\displaystyle \int \!\! \int_D \ \frac{1}{x^2+y^2} \ dA$ where D is: $x^2+y^2 \leq 4$
$\displaystyle \int \!\! \int \!\! \int_E \ dV$ where E is: $x^2+y^2+z^2 \leq 4, \ \ x \geq 0, \ \ y \geq 0, \ \ z \geq 0$

polar coordinates
cylindrical coordinates
spherical coordinates
cartesian coordinates

7.

Evaluate the integral.

$\displaystyle \int_{0}^{7} \int_{-\sqrt{49-x^2}}^{\sqrt{49-x^2}} \int_{-\sqrt{49-x^2-z^2}}^{\sqrt{49-x^2-z^2}} \frac{1}{(x^2+y^2+z^2)^{1/2}} \, dy \, dz \, dx$ =

Answer.

$49\pi $

8.

Use cylindrical coordinates to evaluate the triple integral $\displaystyle \int \!\! \int \!\! \int_{\mathbf{E}} \, \sqrt{x^{2} + y^{2}} \, dV\text{,}$ where E is the solid bounded by the circular paraboloid $z = 1 - 1 \left( x^{2} + y^{2} \right)$ and the $xy$ -plane.

Answer.

$0.837758040957278$

9.

Use spherical coordinates to evaluate the triple integral $\displaystyle \int \!\! \int \!\! \int_{\mathbf{E}} \, x^{2} + y^{2} + z^{2} \, dV\text{,}$ where E is the ball: $x^{2} + y^{2} + z^{2} \leq 4\text{.}$

Answer.

$80.4247719318987$

10.

Find the volume of the solid enclosed by the paraboloids $z = 1 \left( x^{2} + y^{2} \right)$ and $z = 8 - 1 \left( x^{2} + y^{2} \right)\text{.}$

Answer.

$50.2654824574367$

11.

FInd the volume of the ellipsoid $x^2 + y^2 + 6 z^2 = 100\text{.}$

Answer.

$1710.06644021582$

12.

The density, $\delta\text{,}$ of the cylinder $x^2+y^2\le 9\text{,}$ $0\le z\le 4$ varies with the distance, $r\text{,}$ from the $z$-axis:

\[ \delta = 4 + r\mbox{ g}/\mbox{cm}^3. \nonumber \]

Find the mass of the cylinder, assuming $x,y,z$ are in cm.

mass =

(Include units.)

Answer.

$678.584\ {\rm g}$

13.

Suppose $\displaystyle f(x,y,z) = \frac{1}{\sqrt{x^2+y^2+z^2}}$ and $W$ is the bottom half of a sphere of radius $4\text{.}$ Enter $\rho$ as rho, $\phi$ as phi, and $\theta$ as theta.

(a) As an iterated integral,

$\displaystyle \iiint\limits_{W} f \, dV = \int_A^B \!\! \int_C^D \!\! \int_E^F$ $d\rho \, d\phi \, d\theta$

with limits of integration

A =

B =

C =

D =

E =

F =

(b) Evaluate the integral.

Answer. 1

$rho\sin\!\left(phi\right)$

Answer. 2

$0$

Answer. 3

$2\pi $

Answer. 4

$\frac{\pi }{2}$

Answer. 5

$\pi $

Answer. 6

$0$

Answer. 7

$4$

Answer. 8

$\pi \cdot 4^{2}$

14.

In each of the following questions, set up an iterated integral expression whose value determines the desired result. Then, evaluate the integral first by hand, and then using appropriate technology.

Find the volume of the “cap” cut from the solid sphere $x^2 + y^2 + z^2 = 4$ by the plane $z=1\text{,}$ as well as the $z$-coordinate of its centroid.
Find the $x$-coordinate of the center of mass of the portion of the unit sphere that lies in the first octant (i.e., where $x\text{,}$ $y\text{,}$ and $z$ are all nonnegative). Assume that the density of the solid given by $\delta(x,y,z) = \frac{1}{1+x^2+y^2+z^2}\text{.}$
Find the volume of the solid bounded below by the $xy$-plane, on the sides by the sphere $\rho=2\text{,}$ and above by the cone $\phi = \pi/3\text{.}$
Find the $z$ coordinate of the center of mass of the region that is bounded above by the surface $z = \sqrt{\sqrt{x^2 + y^2}}\text{,}$ on the sides by the cylinder $x^2 + y^2 = 4\text{,}$ and below by the $xy$-plane. Assume that the density of the solid is uniform and constant.
Find the volume of the solid that lies outside the sphere $x^2 + y^2 + z^2 = 1$ and inside the sphere $x^2 + y^2 + z^2 = 2z\text{.}$

15.

For each of the following questions,

sketch the region of integration,
change the coordinate system in which the iterated integral is written to one of the remaining two,
evaluate the iterated integral you deem easiest to evaluate by hand.

$\displaystyle \int_{0}^{1} \int_{0}^{\sqrt{1-x^2}} \int_{\sqrt{x^2 + y^2}}^{\sqrt{2-x^2-y^2}} xy\, dz \, dy \, dx$
$\displaystyle \int_{0}^{\pi/2} \int_{0}^{\pi} \int_{0}^{1} \rho^2 \sin(\phi) \, d\rho \, d\phi \, d\theta$
$\displaystyle \int_{0}^{2\pi} \int_{0}^{1} \int_{r}^{1} r^2 \cos(\theta) \, dz \, dr \, d\theta$

16.

Consider the solid region $S$ bounded above by the paraboloid $z = 16 - x^2 - y^2$ and below by the paraboloid $z = 3x^2 + 3y^2\text{.}$

Describe parametrically the curve in $\mathbb{R}^3$ in which these two surfaces intersect.
In terms of $x$ and $y\text{,}$ write an equation to describe the projection of the curve onto the $xy$-plane.
What coordinate system do you think is most natural for an iterated integral that gives the volume of the solid?
Set up, but do not evaluate, an iterated integral expression whose value is average $z$-value of points in the solid region $S\text{.}$
Use technology to plot the two surfaces and evaluate the integral in (c). Write at least one sentence to discuss how your computations align with your intuition about where the average $z$-value of the solid should fall.

11.9: Change of Variables

1.

Find the absolute value of the Jacobian, $\left|\frac{\partial (x,y)}{\partial (s,t)}\right|\text{,}$ for the change of variables given by $x = 6s+8t, y = 4s+8t$

$\left|\frac{\partial(x,y)}{\partial(s,t)}\right| =$

Answer.

$\left|6\cdot 8-8\cdot 4\right|$

2.

Find the Jacobian. $\frac{\partial (x,y,z)}{\partial (s,t,u)}\text{,}$ where $x = 3s+t+4u, y = 2s-t+u, z = 3s+t-5u\text{.}$

$\frac{\partial (x,y,z)}{\partial (s,t,u)} =$

Answer.

$3\cdot \left(-1\cdot \left(-5\right)-1\cdot 1\right)-1\cdot \left(2\cdot \left(-5\right)-1\cdot 3\right)+4\cdot \left(2\cdot 1--1\cdot 3\right)$

3.

Consider the transformation $T: x = \frac{40}{41}u - \frac{9}{41}v, \ \ y = \frac{9}{41}u + \frac{40}{41}v$

A. Compute the Jacobian:

$\frac{\partial(x, y)}{\partial(u, v)} =$

B. The transformation is linear, which implies that it transforms lines into lines. Thus, it transforms the square $S:-41 \leq u \leq 41, -41 \leq v \leq 41$ into a square $T(S)$ with vertices:

T(41, 41) = (, )

T(-41, 41) = (, )

T(-41, -41) = (, )

T(41, -41) = (, )

C. Use the transformation $T$ to evaluate the integral $\int \!\! \int_{T(S)} \ x^2 + y^2 \ {dA}$

Answer. 1

$1$

Answer. 2

$31$

Answer. 3

$49$

Answer. 4

$-49$

Answer. 5

$31$

Answer. 6

$-31$

Answer. 7

$-49$

Answer. 8

$49$

Answer. 9

$-31$

Answer. 10

$7535362.66666667$

4.

Use the change of variables $s=y\text{,}$ $t=y-x^2$ to evaluate $\int\int_R x \,dx\,dy$ over the region $R$ in the first quadrant bounded by $y=0\text{,}$ $y=36\text{,}$ $y=x^2\text{,}$ and $y=x^2-1\text{.}$

$\int\int_R x \,dx\,dy =$

Answer.

$\frac{1\cdot 36}{2}$

5.

Use the change of variables $s = x + y\text{,}$ $t = y$ to find the area of the ellipse $x^2 + 2 x y + 2 y^2 \le 1\text{.}$

area =

Answer.

$\pi $

6.

Use the change of variables $s=xy\text{,}$ $t=xy^2$ to compute $\int_R xy^2\,dA\text{,}$ where $R$ is the region bounded by $xy=1,\ xy=2,\ xy^2=1,\ xy^2=2\text{.}$

$\int_R xy^2\,dA =$

Answer.

$1\cdot 1$

7.

Find positive numbers $a$ and $b$ so that the change of variables $s=ax, t=by$ transforms the integral $\int\int_R \,dx\,dy$ into

\[ \int\int_T \left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert \,ds\,dt \nonumber \]

for the region $R\text{,}$ the rectangle $0\le x \le 30\text{,}$ $0\le y \le 65$ and the region $T\text{,}$ the square $0\le s, t \le 1\text{.}$

$a =$

$b =$

What is $\left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert$ in this case?

$\left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert =$

Answer. 1

$\frac{1}{30}$

Answer. 2

$\frac{1}{65}$

Answer. 3

$30\cdot 65$

8.

Find a number $a$ so that the change of variables $s=x+ay, t=y$ transforms the integral $\int\int_R \,dx\,dy$ over the parallelogram $R$ in the $xy$-plane with vertices $(0,0)\text{,}$ $(18,0)\text{,}$ $(-24,8)\text{,}$ $(-6,8)$ into an integral

\[ \int\int_T \left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert\,ds\,dt \nonumber \]

over a rectangle $T$ in the $st$-plane.

$a =$

What is $\left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert$ in this case?

$\left\vert \frac{\partial(x,y)}{\partial(s,t)}\right\vert =$

Answer. 1

$\frac{-1\cdot \left(-24\right)}{8}$

Answer. 2

$1$

9.

In this problem we use the change of variables $x=4 s + t\text{,}$ $y = s - 3 t$ to compute the integral $\int_R (x+y)\,dA\text{,}$ where $R$ is the parallelogram with vertices $(x,y)=(0,0)\text{,}$ $(4,1)\text{,}$ $(7,-8)\text{,}$ and $(3,-9)\text{.}$

First find the magnitude of the Jacobian, $\left|\frac{\partial(x,y)}{\partial(s,t)}\right| =$.

Then, with $a =$, $b =$,

$c =$, and $d =$,

$\int_R (x+y)\,dA = \int_a^b\,\int_c^d\, ($ $s +$ $t +$ $)\; dt\, ds$ =

Answer. 1

$4\cdot 3+1$

Answer. 2

$0$

Answer. 3

$\frac{3\cdot 4+1}{1+4\cdot 3}$

Answer. 4

$0$

Answer. 5

$\frac{3-4\cdot \left(-9\right)}{4\cdot 3+1}$

Answer. 6

$13\cdot \left(4+1\right)$

Answer. 7

$13\cdot \left(1-3\right)$

Answer. 8

$0$

Answer. 9

$\frac{\left(3\cdot 4+1\right)\!\left(3-4\cdot \left(-9\right)\right)\!\left(3+1+4\cdot 1-4\cdot \left(-9\right)+3\cdot \left(4+4\cdot 4-3+4\cdot \left(-9\right)\right)\right)}{2\cdot \left(1+4\cdot 3\right)^{2}}$

10.

Let $D'$ be the region in the $xy$-plane that is the parallelogram with vertices $(3,3)\text{,}$ $(4,5)\text{,}$ $(5,4)\text{,}$ and $(6,6)\text{.}$

Sketch and label the region $D'$ in the $xy$-plane.
Consider the integral $\iint_{D'} (x+y) \, dA\text{.}$ Explain why this integral would be difficult to set up as an iterated integral.
Let a change of variables be given by $x = 2u + v\text{,}$ $y = u + 2v\text{.}$ Using substitution or elimination, solve this system of equations for $u$ and $v$ in terms of $x$ and $y\text{.}$
Use your work in (c) to find the pre-image, $D\text{,}$ which lies in the $uv$-plane, of the originally given region $D'\text{,}$ which lies in the $xy$-plane. For instance, what $uv$ point corresponds to $(3,3)$ in the $xy$-plane?
Use the change of variables in (c) and your other work to write a new iterated integral in $u$ and $v$ that is equivalent to the original $xy$ integral $\iint_{D'} (x+y) \, dA\text{.}$
Finally, evaluate the $uv$ integral, and write a sentence to explain why the change of variables made the integration easier.

11.

Consider the change of variables

\[ x(\rho, \theta, \phi) = \rho \sin(\phi) \cos(\theta) \ \ \ \ \ y(\rho, \theta, \phi) = \rho \sin(\phi) \sin(\theta) \ \ \ \ \ z(\rho, \theta, \phi) = \rho \cos(\phi), \nonumber \]

which is the transformation from spherical coordinates to rectangular coordinates. Determine the Jacobian of the transformation. How is the result connected to our earlier work with iterated integrals in spherical coordinates?

12.

In this problem, our goal is to find the volume of the ellipsoid $\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1\text{.}$

Set up an iterated integral in rectangular coordinates whose value is the volume of the ellipsoid. Do so by using symmetry and taking 8 times the volume of the ellipsoid in the first octant where $x\text{,}$ $y\text{,}$ and $z$ are all nonnegative.
Explain why it makes sense to use the substitution $x = as\text{,}$ $y = bt\text{,}$ and $z = cu$ in order to make the region of integration simpler.
Compute the Jacobian of the transformation given in (b).
Execute the given change of variables and set up the corresponding new iterated integral in $s\text{,}$ $t\text{,}$ and $u\text{.}$
Explain why this new integral is better, but is still difficult to evaluate. What additional change of variables would make the resulting integral easier to evaluate?
Convert the integral from (d) to a new integral in spherical coordinates.
Finally, evaluate the iterated integral in (f) and hence determine the volume of the ellipsoid.

	\(x = 3\)	\(x = 3.3\)	\(x = 3.6\)
\(y = 4\)	7	9	12
\(y = 4.4\)	5	7	9
\(y = 4.8\)	3	5	18

\(v \backslash T\)	\(-20\)	\(-15\)	\(-10\)	\(-5\)	\(0\)	\(5\)	\(10\)	\(15\)	\(20\)
\(5\)	\(-34\)	\(-28\)	\(-22\)	\(-16\)	\(-11\)	\(-5\)	\(1\)	\(7\)	\(13\)
\(10\)	\(-41\)	\(-35\)	\(-28\)	\(-22\)	\(-16\)	\(-10\)	\(-4\)	\(3\)	\(9\)
\(15\)	\(-45\)	\(-39\)	\(-32\)	\(-26\)	\(-19\)	\(-13\)	\(-7\)	\(0\)	\(6\)
\(20\)	\(-48\)	\(-42\)	\(-35\)	\(-29\)	\(-22\)	\(-15\)	\(-9\)	\(-2\)	\(4\)
\(25\)	\(-51\)	\(-44\)	\(-37\)	\(-31\)	\(-24\)	\(-17\)	\(-11\)	\(-4\)	\(3\)
\(30\)	\(-53\)	\(-46\)	\(-39\)	\(-33\)	\(-26\)	\(-19\)	\(-12\)	\(-5\)	\(1\)
\(35\)	\(-55\)	\(-48\)	\(-41\)	\(-34\)	\(-27\)	\(-21\)	\(-14\)	\(-7\)	\(0\)