2.14: Project- Hard Definition of Derivative Problems
( \newcommand{\kernel}{\mathrm{null}\,}\)
Purpose of the project: Struggle through a difficult but important calculus problem.
Each of the following is a difficult definition of the derivative problem. Your group will be assigned one of the following, and then you can present the solution to the class. In each case, the “stuff in the example box” is not your problem, but look at it and hopefully it will help with your problem.
- Let f(x)=x4. Using the definition of the derivative, find f′(x).
Simplify (x+1)4.We can do this problem by splitting it up into (x+1)2(x+1)2. We know (x+1)2=x2+2x+1 — that means
(x+1)4=(x2+2x+1)(x2+2x+1)
To solve from here, we need to multiply every term of (x2+2x+1) by x2, then every term by 2x, then every term by 1, and add it all up. Here we go:
(x+1)4=(x2+2x+1)(x2+2x+1)=(x2+2x+1)x2+(x2+2x+1)2x+(x2+2x+1)1=x4+2x3+x2+2x3+4x2+2x+x2+2x+1=x4+4x3+6x2+4x+1.
- Let f(x)=√x. Using the definition of the derivative, find f′(x) (which can also be written ddxf(x) or dfdx).
Rationalize the numerator of √x+1−√xx.
To “rationalize the numerator”, the trick is to multiply top and bottom by what is known as the conjugate: it is the same as the numerator, only the sign is flipped so that subtraction becomes addition or vice versa. In this case, the conjugate is √x+1+√x. We see
√x+1−√xx=(√x+1−√x)(x)⋅(√x+1+√x)(√x+1+√x)=(√x+1−√x)(√x+1+√x)(x)(√x+1+√x)=(√x+1)2−(√x)2x(√x+1+√x)=x+1−xx(√x+1+√x)=1x(√x+1+√x)
The numerator is now rationalized.
- Let f(x)=sin(x). Using the definition of the derivative, find f′(x) (which can also be written ddxf(x) or dfdx). There are three facts we need to compute this derivative:
- sin(A+B)=sin(A)cos(B)+cos(A)sin(B)
- limh→0sin(h)h=1
- limh→0cos(h)−1h=0
Find limh→0sin(y+h)−sin(y)cos(h)h.In this example, we use the first fact listed above to write sin(y+h)=sin(y)cos(h)+cos(y)sin(h). We have the original problem is equal to
=limh→0sin(y)cos(h)+cos(y)sin(h)−sin(y)cos(h)h=limh→0cos(y)sin(h)h=limh→0sin(h)h⋅cos(y)=1⋅cos(y)=cos(y)
Notice towards the end we used limh→0sin(h)h=1.
- Let f(x)=ex. Using the definition of the derivative, find f′(x) (which can also be written ddxf(x) or dfdx). Use the limit we found on the homework yesterday: limh→0eh−1h=1.
Helpful example: Simplify ex+1+e1ex+1.
Recall that ex+1=exe1. Hence this becomes
ex+1+e1ex+1=exe1+e1ex+1=e1(ex+1)ex+1=e1=e
- Let f(x)=1x. Using the definition of the derivative, find f′(x) (which can also be written ddxf(x) or dfdx).
Simplify 1x+1−1xx.
In this example, we want to clear the denominators from this tricky double fraction. To do this, we will multiply by both denominators: x(x+1).
1x+1−1xx=(1x+1−1x)x⋅x(x+1)x(x+1)=(1x+1−1x)x(x+1)(x)(x)(x+1)=(x(x+1)x+1−x(x+1)x)x2(x+1)=x−(x+1)x2(x+1)=−1x2(x+1)
- Let f(x)=ln(x). Using the definition of the derivative, find f′(x) (which can also be written ddxf(x) or dfdx). We will need the following facts:
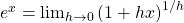
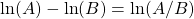
- nln(A)=ln(An)
- ln(ex)=x
(Example 1): Rewrite ln(x+5)−ln(x)2 as the natural log of a single quantity.We need to use some log rules to simplify this. First we use
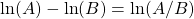 .
.ln(x+5)−ln(x)2=ln(x+5x)2=ln(1+5x)2
Now we use nln(A)=ln(An), thinking of the division by 2 as a multiplication by
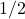 .(Example 2): Simplify
.(Example 2): Simplify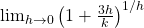 .
.
In this example, we know from our facts above that
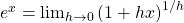 . We also see that
. We also see thatNotice now that 3k is playing the same role as x in the ex equation. So this simplifies to
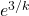 .
.


