7.7: Integration by Parts

Last updated
Save as PDF

Page ID: 88690

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Recall the product rule:

$\cfrac{d}{dx} f \cdot g = f g' + g f'$

If we use $u$ and $v$ instead of $f$ and $g$, this becomes

$\frac{d}{dx} u \cdot v = u v' + v u'.$

Now let’s integrate both sides and solve for $u v'$

\[\begin{align*} \frac{d}{dx} u \cdot v & = u v' + v u' \\ \int \frac{d}{dx} uvdx & = \int u v' + v u'dx \\ uv & = \int u v'dx + \int v u' dx \\ uv - \int v u'dx & = \int u v'dx, \end{align*}\]

Flipping this around, we have the inverse product rule, also called integration by parts.

$\boxed{\int u v'dx = uv - \int u' v}$

The tricky part is what to use as $u$, and what to use as $v'$. Here are some steps and guidelines to follow, but it takes some intuition building before you know how to use it sometimes, and some product integrals cannot be solved with integration by parts.

Integration by parts:

Think of your original integral as a product. Identify a function that is easy to integrate, and set it equal to $v'$. The other function should be something that will simplify nicely once you take the derivative.
Find $u'$ (take the derivative of $u$) and find $v$ (integrate $v'$)
Using substitution, plug in the values for $u$, $v$, $v$ and $u'$ in the integration by parts formula.
This gives you another integral — hopefully this one is easier. If not, you may need to use $u$-substitution, or even integration by parts a second time.

Integration by parts

Find $\int_0^2 x e^xdx$.

Let’s follow the integration by parts steps:

The function we are integrating is $x e^x$, which is a product in two pieces: $x$ and $e^x$. While $x$ is easy to integrate, $e^x$ is even nicer. We will start with $v' = e^x$, and $u = x$.
We see $u' = \frac{d}{dx} x = 1$, and $v = \int e^xdx = e^x$ (you don’t need to worry about the $+ C$ for now).
Using the formula with $u = x$, $u' = 1$, $v = e^x$, and $v' = e^x$, we have
\[\begin{align*} \int_0^2 x e^xdx & = uv - \int u' vdx \\ & = (x)(e^x) - \int_0^2 (1)(e^x)dx \\ & = x e^x - \int_0^2 e^xdx \\ \end{align*}\]
We now have reduce the problem to an easier one: $\int e^xdx$. We continue:
\[\begin{align*} \int_0^2 x e^xdx & = x e^x - \int_0^2 e^xdx \\ & = x e^x - e^x \Big|_0^2 \\ & = (2 e^2 - e^2) - (0e^0 - e^0) \\ & = (e^2) - (0 - 1) \\ & = e^2 + 1 \end{align*}\]

So the answer is $e^2 + 1 \approx \boxed{8.389}$.

Notice if the problem contains an $x$ variable, then this is usually a good choice for $u$ since it will go away once you take the derivative $u'$.

Integration by parts

Compute $\int (2x + 3) \cos(x)dx$.

We following the steps of integration by parts.

Set $u = (2x + 3)$, which simplifies nicely with the derivative, and let $v' = \cos(x)$ which is easy to integrate.
We have $u' = 2$, and $v = \sin(x)$.
Applying the formula, we have
\[\begin{align*} \int (2x + 3) \cos(x)dx & = uv - \int u' vdx \\ & = (2x + 3) \sin(x) - \int 2 \sin(x)dx \\ \end{align*}\]
Continuing …
\[\begin{align*} \int (2x + 3) \cos(x)dx & = (2x + 3) \sin(x) - \int 2 \sin(x)dx \\ & = (2x + 3) \sin(x) - 2 (-\cos(x)) \\ & = \boxed{(2x + 3) \sin(x) + 2 \cos(x) + C}. \end{align*}\]

Integration by parts

Use integration by parts to find $\int x \sqrt{2x + 1}dx$

This one will involve integration by parts and a $u$-substitution shortcut. Here are the steps of integration by parts:

We can integrate either function, but just like the previous case it’s best to set $u = x$. This leaves $v' = \sqrt{2x + 1}$.
We see $u' = \frac{d}{dx} x = 1$. Notice $v = \int \sqrt{2x + 1}dx$ is a bit harder — this is a $u$-sub shortcut though. Let’s write it as $\frac{1}{m}$ factor from the $u$-sub shortcut, we have
$quicklatex.com-4e50229ea75bc36d45c4b803fa999895_l3.png$
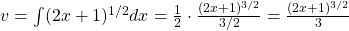
Applying the formula with $u = x$, $u' = 1$, $v' = \sqrt{2x + 1}$, we see

At this point, doing the integral of $u$-sub shortcut problem. Watch.

Search

Text Color

Text Size

Margin Size

Font Type