3.6: Derivatives of Logarithmic Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
As with the sine, we do not know anything about derivatives that allows us to compute the derivatives of the exponential and logarithmic functions without going back to basics. Let's do a little work with the definition again:
ddxax=limΔx→0ax+Δx−axΔx=limΔx→0axaΔx−axΔx=limΔx→0axaΔx−1Δx=axlimΔx→0aΔx−1Δx.
There are two interesting things to note here: As in the case of the sine function we are left with a limit that involves Δx but not x, which means that whatever limΔx→0(aΔx−1)/Δx is, we know that it is a number, that is, a constant. This means that ax has a remarkable property: its derivative is a constant times itself.
We earlier remarked that the hardest limit we would compute is limx→0sinx/x=1; we now have a limit that is just a bit too hard to include here. In fact the hard part is to see that limΔx→0(aΔx−1)/Δx even exists---does this fraction really get closer and closer to some fixed value? Yes it does, but we will not prove this fact.
We can look at some examples. Consider (2x−1)/x for some small values of x: 1, 0.828427124, 0.756828460, 0.724061864, 0.70838051, 0.70070877 when x is 1, 1/2, 1/4, 1/8, 1/16, 1/32, respectively. It looks like this is settling in around 0.7, which turns out to be true (but the limit is not exactly 0.7). Consider next (3x−1)/x: 2, 1.464101616, 1.264296052, 1.177621520, 1.13720773, 1.11768854, at the same values of x. It turns out to be true that in the limit this is about 1.1.
Two examples don't establish a pattern, but if you do more examples you will find that the limit varies directly with the value of a: bigger a, bigger limit; smaller a, smaller limit. As we can already see, some of these limits will be less than 1 and some larger than 1. Somewhere between a=2 and a=3 the limit will be exactly 1; the value at which this happens is called e, so that
limΔx→0eΔx−1Δx=1.
As you might guess from our two examples, e is closer to 3 than to 2, and in fact e≈2.718.
Now we see that the function ex has a truly remarkable property:
ddxex=limΔx→0ex+Δx−exΔx=limΔx→0exeΔx−exΔx=limΔx→0exeΔx−1Δx=exlimΔx→0eΔx−1Δx=ex.
That is, ex is its own derivative, or in other words the slope of ex is the same as its height, or the same as its second coordinate: The function f(x)=ex goes through the point (z,ez) and has slope ez there, no matter what z is. It is sometimes convenient to express the function ex without an exponent, since complicated exponents can be hard to read. In such cases we use exp(x), e.g., exp(1+x2) instead of e1+x2.
What about the logarithm function? This too is hard, but as the cosine function was easier to do once the sine was done, so the logarithm is easier to do now that we know the derivative of the exponential function. Let's start with logex, which as you probably know is often abbreviated lnx and called the "natural logarithm'' function.
Consider the relationship between the two functions, namely, that they are inverses, that one "undoes'' the other. Graphically this means that they have the same graph except that one is "flipped'' or "reflected'' through the line y=x, as shown in Figure 3.6.1.
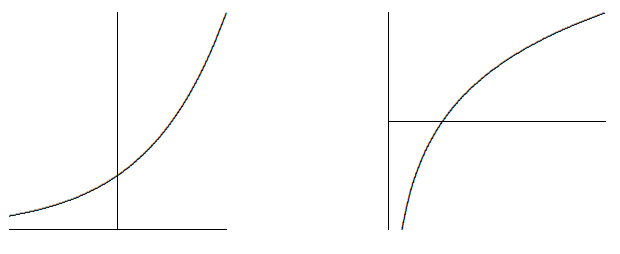
This means that the slopes of these two functions are closely related as well: For example, the slope of ex is e at x=1; at the corresponding point on the ln(x) curve, the slope must be 1/e, because the "rise'' and the "run'' have been interchanged. Since the slope of ex is e at the point (1,e), the slope of ln(x) is 1/e at the point (e,1).
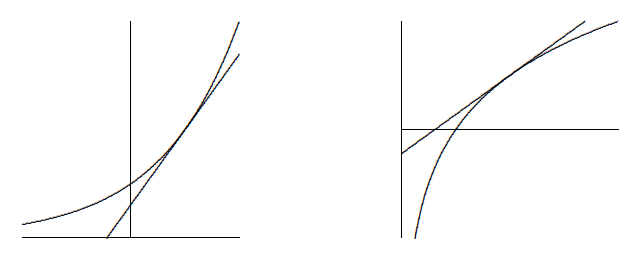
More generally, we know that the slope of ex is ez at the point (z,ez), so the slope of ln(x) is 1/ez at (ez,z), as indicated in Figure 3.6.2. In other words, the slope of lnx is the reciprocal of the first coordinate at any point; this means that the slope of lnx at (x,lnx) is 1/x. The upshot is: ddxlnx=1x. We have discussed this from the point of view of the graphs, which is easy to understand but is not normally considered a rigorous proof---it is too easy to be led astray by pictures that seem reasonable but that miss some hard point. It is possible to do this derivation without resorting to pictures, and indeed we will see an alternate approach soon.
Note that lnx is defined only for x>0. It is sometimes useful to consider the function ln|x|, a function defined for x≠0. When x<0, ln|x|=ln(−x) and
ddxln|x|=ddxln(−x)=1−x(−1)=1x.
Thus whether x is positive or negative, the derivative is the same.
What about the functions ax and logax? We know that the derivative of ax is some constant times ax itself, but what constant? Remember that "the logarithm is the exponent'' and you will see that a=elna. Then ax=(elna)x=exlna, and we can compute the derivative using the chain rule:
ddxax=ddx(elna)x=ddxexlna=(lna)exlna=(lna)ax.
The constant is simply lna. Likewise we can compute the derivative of the logarithm function logax. Since x=elnx we can take the logarithm base a of both sides to get loga(x)=loga(elnx)=lnxlogae. Then
ddxlogax=1xlogae.
This is a perfectly good answer, but we can improve it slightly. Since
a=elnaloga(a)=loga(elna)=lnalogae1=lnalogae1lna=logae,
we can replace logae to get ddxlogax=1xlna.
You may if you wish memorize the formulas
ddxax=(lna)axandddxlogax=1xlna.
Because the "trick'' a=elna is often useful, and sometimes essential, it may be better to remember the trick, not the formula.
Compute the derivative of f(x)=2x.
Solution
ddx2x=ddx(eln2)x=ddxexln2=(ddxxln2)exln2=(ln2)exln2=2xln2
Compute the derivative of f(x)=2x2=2(x2).
ddx2x2=ddxex2ln2=(ddxx2ln2)ex2ln2=(2ln2)xex2ln2=(2ln2)x2x2
Compute the derivative of f(x)=xx. At first this appears to be a new kind of function: it is not a constant power of x, and it does not seem to be an exponential function, since the base is not constant. But in fact it is no harder than the previous example.
ddxxx=ddxexlnx=(ddxxlnx)exlnx=(x1x+lnx)xx=(1+lnx)xx
Recall that we have not justified the power rule except when the exponent is a positive or negative integer. We can use the exponential function to take care of other exponents.
ddxxr=ddxerlnx=(ddxrlnx)erlnx=(r1x)xr=rxr−1

