Applications: Free Falling Bodies

An object in motion is characterized by a changing position as a function of time. The derivative of the distance function with respect to time gives us the velocity of the object as a function of time. Furthermore the derivative of the velocity function, gives us the acceleration of the object as a function of time. But what causes an object to move? To understand particle dynamics we need to first understand the concept of force.

Newton's first law of motion states that an object in motion will remain in motion until acted on by a force. This observation is one of most important ones ever made as it offers a way of defining what a force is. According to this law, an object traveling in space at 100,000 km/hr will remain at that velocity forever provided no force acts on it.

For example, if you were to throw a ball in space it would forever continue in the samedirection along with the same velocity with which it left your hand. Here, space refers to anywhere that is free from the influence of any gravitational force, electro-magnetic force, air-resistance or any other forces. Once set in motion an object will continue with that same velocity forever.

Since no force is required to keep an object in motion, then a force can be defined as that which changes the velocity of the object. Thus force is a measure of a resistance to a change in motion. Since motion is characterized by a constant velocity, then a change in motion results in a change in velocity. By definition, a change in velocity is an acceleration.

This simple, yet profound conclusion tells us that forces are defined by accelerations. The force required to accelerate an object is proportional to the magnitude of the acceleration. The mass of the object is also a factor since the greater the mass, the greater its resistance to motion. Observation shows that the resistance to a change in motion is directly dependent on the amount of matter being accelerated.

We can define a Newton as the force equipped accelerate a body of unit mass, 1 kg, \(a\frac{m}{s^2}\) Therefore to accelerate a body of mass, \(m\), the required force would be \(m\) times \(a\).

\[\text{Force}=\text{mass}\times\text{acceleration} \nonumber \]

\[F(m,a)=ma \nonumber \]

This is read as, the force required to accelerate a body is directly related to its mass and the magnitude of the acceleration of the mass. The important concept to understand is that forces are defined as accelerations or changes in velocity. It requires no force to keep a body in motion Once in motion it will remain in motion. A force is required only to change its velocity or accelerate it. Thus force is a quantifiable measurement of a mass’s resistance to a change in motion. If an object had no resistance to a change in motion then there would be no such thing as force!

This might seem to contradict reason. One can better understand this by considering an airplane flying in space, where space is some imaginary place that contains no matter or force fields inside it. If its four engines produce an acceleration \(5\frac{m}{s^2}\) and the mass of the plane is \(8x10^6\) kg, then the thrust or force acting on the plane is \((5)\cdot(8x10^6=4x10^7)\). If we assume an inexhaustible and weightless fuel source then theoretically the engines will push the plane forward with a constant force of 4 million newtons.

Now since the plane is flying in an imaginary space under a constant force, it is free to accelerate forever. Remember forces are defined as accelerations and not velocities. The plane will accelerate at a constant acceleration of \(5\frac{m}{s^2}\). This means the planes velocity would increases and increase at the rate of \(5\dfrac{\frac{m}{s}}{s}\). The graph of its velocity as a function of time would be a linearly increasing function:

\[v(t)=5{\cdot}t \nonumber \]

The derivative of the velocity function is the acceleration function:

\[a(t)=\dfrac{dv}{dt}=5 \nonumber \]

The fundamental concept to understand here is that a force is required only to change an objects velocity. A change in velocity is by definition an acceleration. Therefore forces are required only to accelerate an object. A constant force acting on a body will accelerate the body with a constant acceleration, which means the body’s velocity will increase and increase forever, all due to a constant force. Furthermore the greater the mass, the greater its resistance to a change in velocity. Thus, the force required to accelerate a mass is directly proportional to its mass.

Understanding Free Fall Motion

Having laid down the conceptual basis of what velocity, acceleration and forces are, we can now study the motion of free falling bodies on earth. An object falls to earth because of the gravitational force of attraction that the earth experiences for the object. What then is gravity? From Newton’s law of gravitation, the force attracting two bodies is given by:

\[F_{\text{gravitational}}=G \cdot \dfrac{m_1{\cdot}m_2}{d^2} \;\text{ ( G is the gravitational constant) } \nonumber \]

To derive this, think of a unit mass of 1 kg separated a distance from a larger mass, M. The gravitational force is the force of attraction the larger mass expresses for the unit mass and vice-versa. Observation confirms that the gravitational force is proportional to mass the larger body and decreases with the square of the distance separating them. The reason it is distance squared and not just directly related to the distance is because masses are 3-dimensional. In 3-dimensional space, properties are related to the projected areas as opposed to 2-dimensional geometry that are dependent on the length only. Therefore, the gravitational force between the two masses is:

\[ F_{\text{gravitational}}=c \cdot \dfrac{M\cdot1}{d^2} \;\text{ ( c is the some constant) } \nonumber \]

If the unit mass was replaced by a mass m, the force of attraction would be m times the amount it was with the unit mass.

\[ F_{\text{gravitational}}=G \cdot \dfrac{M_1 {\cdot} m_2}{d^2} \nonumber \]

\(G\) replaces \(c\) as a gravitational constant determined from experiments. The gravitational force of earth acting on a body of mass \(m_1\) located near the surface of the earth is then:

\[F_\text{gravity} =G \cdot \dfrac{m_{earth} {\cdot} m_1}{d^2} \nonumber \]

Since most of our free falling bodies occur near the surface of the earth, we can take \(d\), to be the radius of the earth. Substituting the known values in along with the value for \(G\), reduces the equation to:

\[F_\text{gravity} =9.8 {\cdot} m_1 \nonumber \]

Since force equal \(ma\), we have:

\[\begin{align} m_1 {\cdot} a&=9.8{\cdot}m_1 \\ a=9.8 \end{align} \nonumber \]

This important result tells us that the acceleration of a body of any mass is 9.8 meters per second per second near the surface of the earth. The gravitational force acting on a body near the surface of the earth would be its mass, m, times the constant acceleration, 9.8. For those who have a ground to hold them up this does not mean much but for a free-falling body in air its acceleration as it falls toward the earth will be a constant \(9.8\frac{m}{s^2}\), regardless of its mass. A body of twice the mass will be pulled in by twice the force, but the acceleration due to the force of gravity remains the same.

This may sound a bit confusing but just remember any body will fall to the earth with a constant acceleration, independent of its mass. In terms of particle motion, mass means nothing for a falling body! While the gravitational force increases with mass, the acceleration remains the same.

We can now write the acceleration function for a falling body near the earth’s surface as:

\[a(t)= 9.8\frac{m}{s^2} \;\text{ (Constant)} \nonumber \]

Since acceleration as a function of time is by definition the derivative of the velocity function with respect to time then what we have is the same as:

\[\begin{align} a(t)=\dfrac{dv}{dt}&=v'(t) \\ {\therefore} v'(t)&=9.8 \end{align} \nonumber \]

The derivative of the velocity function (acceleration) is 9.8. Since we know that the derivative of any function \(c {\cdot} x^n\) is \(c{\cdot}nx^{n-1}\), then we can easily find the velocity function since we know what its derivative is.

The process of finding a function, given its derivative is known as anti-differentiation. In this case 9.8 can also be written as \(9.8{\cdot}t^0 \; (t^0=1)\). We see that:

\[(n-1)=0 \nonumber \]

Therefore \(n\) equals 1. Consequently the anti-derivative of \(9.8{\cdot}t^0\) is \(9.8{\cdot}t\). This should hopefully be obvious since the derivative of \(v(t)=9.8{\cdot}t\) is just \(v'(t)=9.8\). We now know that velocity as a function of time is:

\[v(t)=9.9{\cdot}t \nonumber \]

whose derivative with respect to time is:

\[v'(t)=a(t)=9.8 \nonumber \]

The graph of the velocity function is a linearly increasing function with constant rate of change or slope \(9.8 \frac{m}{s^2}\)

This graph of the velocity function gives us the objects velocity as any time \(t\), assuming that air-resistance is negligible. For example at \(t= 10\) seconds, the object’s velocity is:

\[v(t)=9.8{\cdot}10-98\frac{m}{s} \nonumber \]

At \(t= 94\) seconds its velocity is:

\[ v(94)=9.8 \cdot 94 = 921 \,\dfrac{m}{s} \nonumber \]

Or almost \(30,000 \frac{km}{hr}\). Due to air-resistance no object reaches such high velocities. Remember the greater the height it is dropped from the more time it has to increase its velocity or accelerate before it slams into the earth.

Now how do we find the distance function or the distance covered from the point of dropping the object. From the definition of velocity we know that:

\[\begin{align} v(t)=\frac{ds}{dt}&=s'(t) \\ {\therefore}s'(t)=9.8t \end{align} \nonumber \]

Since \(s'(t)=9.8{\cdot}t\), we have \(n=1\) so its anti-derivative will be \(9.8{\cdot}\frac{t^2}{2}\), where the derivative of \(c{\cdot}\frac{t^2}{2}\) is \(c{\cdot}t\), \(ct = 9.8t\). The solution is then:

\[d(t)=9.8{\cdot}\frac{t^2}{2} (\text{ or } \; 4.9{\cdot}t^2) \nonumber \]

The derivative of this function is the velocity function or

\[v(t) = 9.8\,t \nonumber \]

We can graph the distance function \(d(t)=9.8{\cdot}\frac{t^2}{2}\). The graph gives us the vertical distance traveled from where it was dropped at any time \(t\).

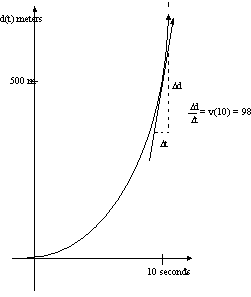
Clearly as time, \(t\), increases, the rate at which distance is being covered is very great . For example between \(t= 0 s\) to \(t =5s\), the object has covered totally.

\[d(5)-d(t)=9.8{\cdot}5^2-0=122.5 \text{ meters} \nonumber \]

Or the object has covered 112.5 meters in the first five seconds of its free-fall. However from \(t = 20s \) to \(t = 25 s\), the object has covered:

\[d(25) -d(20) = 9.8{\cdot}\dfrac{25^2}{2}-9.8{\cdot}\dfrac{20^2}{2} = 1102.5 \text{ meters} \nonumber \]

The object has covered more than a kilometer during this five second interval!! This should make sense because initially the body’s velocity is small and thus does not cover much distance over a time interval \({\Delta} t\). However, after some time its velocity has increased (look at the graph of the velocity function graph), such that over a same interval \({\Delta}t\), the object covers a greater distance. Remember constant acceleration means that the velocity is increasing linearly with time and distance increases with the half square of time.

Initial Conditions of Motion

The concepts of forces, accelerations, velocities and distance are not limited to free-fall motion. Constant accelerations exist in many other physical phenomena’s. Before ending we need to understand how we can modify our equations of motion to be consistent with any initial conditions that may exist. For example, a ball may be dropped with an initial velocity or a car may accelerate from a certain distance from a starting point.

If an object was moving at constant velocity, \(v_c\), its velocity function would be

\[ v(t) = v_c \nonumber \]

that is, a constant at any time, \(t\).

From the definition of the derivative, the derivative of a constant function of the form \(f(x)=c\) is zero because:

\[ \lim_{\Delta{x} \rightarrow 0} \dfrac{f(x+\Delta{x}) - f(x)}{\Delta{x}} = \dfrac{c-c}{\Delta{x}}=\dfrac{0}{\Delta{x}}=0 \nonumber \]

Therefore the derivative of the velocity function is:

\[ v'(t)=a(t)=0 \nonumber \]

when \(v_c\) is a constant

Looking back at our free-falling body, we know that its acceleration was \(9.8\, \frac{m}{s^2}\). This can now be written as:

\[v('(t)=a(t)=9.8 \, \dfrac{m}{s^2} + 0 \nonumber \]

The anti-derivative of this acceleration function is then:

\[ v(t) - 9.8 \, t + v_i \nonumber \]

Remember that the anti-derivative of zero is a constant. At \(t=0\) we have the initial condition:

\[v(0)=0+v_i \nonumber \]

\[v(0)=v_i \nonumber \]

With \(v_i\) is the velocity of the object at \(t = 0\). It represents a situation that may exist when the initial condition is zero. When anti-differentiating we need to remember to add a constant along to reflect the initial conditions that may exist in the situation. For example if a car is traveling down the highway at 82 mph, suddenly sees a cop, and then steps on the pedal, accelerating the cart at 3 mph/s, then its velocity at any time t, were t is measured as soon as he steps on the gas is:

\[ v(t) = 82 + 3\,t \nonumber \]

We know that the velocity function of a free-falling body is:

\[ v(t) = 9.8\,t + v_i + 0 \nonumber \]

The anti-derivative of this function gives us the distance covered as a function of time:

\[ d(t) = 9.8 \dfrac{t^2}{2}+v_i\,t+d_i \nonumber \]

\(d_i\) is the objects initial position at \(t=0\). Our result can be generalized for initial acceleration \((a_i)\; (v_i)\) or distance as follows:

\[a(t)=a+0+0 \nonumber \]

\[v(t)=a{\cdot}t+v_i+0 \nonumber \]

\[d(t)=a{\cdot}\dfrac{t^2}{2}+v_i{\cdot}t+d_i \nonumber \]

Questions

1. Consider the following three cases for a free-falling body:

   1 - A ball is dropped from rest from the top of a building.

   2 - A similar ball is dropped from the same spot with an initial velocity of 10 m/s

   Find the distance function (distance covered as a function of time) for each case.

2. Consider three cars that pass a certain starting point.

   Car 1 - starts from rest with a constant acceleration of 6 m/s/s

   Car 2 - Has an initial velocity of 50 km/hr and maintains this constant velocity with no acceleration.

   Car 3 - Has an initial velocity of 20 km/hr and an acceleration of 4 km/hr/ sec

   Car 4 - starts 5 km in front of all the other cars with no initial velocity but an acceleration of 7 km/hr/sec.

   Derive the distance function for each car with reference to the distance covered from the staring point.

   Graph the distance function for each car.

3. Last, determine at which distance each car will pass each other. You can do this by either looking at where the graphs of the paths intersect or by setting the distance functions equal to each other and solving for time.

Solutions

• \(d(t) = 4.9t^2\)
• \(d(t) = 4.9t^2 + 10t\)
• \(car1: d(t)=10.8t^2\)
• car2: \(d(t)=50t\)
• car3: \(d(t)=2t^2 + 20t\)
• car4: \(d(t)=3.5t^2 + 5\)
• car1 and car2 intersect at about 235 m at a time of about 4.8 seconds
• car1 and car3 intersect at about 55 m at a time of about 2.4 seconds
• car1 and car4 intersect at about 10 m at a time of about 1 second
• car3 and car4 intersect at about 6 m at a time of about .5 seconds
• car2 and car3 seem to never intersect, unless the intersection is at time much greater than 6 seconds

• Faraz Hussain, Copied in whole or part from UnderstandingCalculus.com