2.2.E: Best Affine Approximations (Exercises)

Exercise \(\PageIndex{1}\)

Find the derivative of each of the following functions.

(a) \(f(t)=\left(t^{3}, t, 2 t+4\right)\)

(b) \(g(t)=(3 t \cos (2 t), 4 t \sin (2 t))\)

(c) \(h(t)=\left(4 t^{3}-3, \sin (t), e^{-2 t}\right)\)

(d) \(f(t)=\left(e^{-t} \sin (3 t), e^{-t} \cos (3 t), t e^{-t}\right)\)

Answer

(a) \(D f(t)=\left(3 t^{2}, 1,2\right)\)

(c) \(D h(t)=\left(12 t^{2}, \cos (t),-2 e^{-2 t}\right)\)

Exercise \(\PageIndex{2}\)

For each of the following, find the best affine approximation to \(f\) at the given point.

(a) \(f(t)=\left(t, t^{3}\right), t=2\)

(b) \(f(t)=(3 \sin (2 t), 4 \cos (2 t)), t=\frac{\pi}{6}\)

(c) \(f(t)=(\cos (t), \sin (t), \cos (2 t)), t=\frac{\pi}{3}\)

(d) \(f(t)=(2 \cos (2 t), 3 \sin (2 t), 3 t), t=0\)

Answer

(a) \(A(t)=(1,12)(t-2)+(2,8)\)

(c) \(A(t)=\left(-\frac{\sqrt{3}}{2}, \frac{1}{2},-\sqrt{3}\right)\left(t-\frac{\pi}{3}\right)+\left(\frac{1}{2}, \frac{\sqrt{3}}{2},-\frac{1}{2}\right)\)

Exercise \(\PageIndex{3}\)

Let \(f(t)=(2 \cos (\pi t), 3 \sin (\pi t))\) parametrize an ellipse \(E\) in \(\mathbb{R}^2\). Plot \(E\) along with the tangent line at \(f\left(\frac{2}{3}\right)\).

Exercise \(\PageIndex{4}\)

Let \(f(t)=((1+2 \cos (t)) \cos (t),(1+2 \cos (t)) \sin (t))\) parametrize a curve \(C\) in \(\mathbb{R}^2\). Plot \(C\) along with the tangent line at \(f\left(\frac{\pi}{6}\right)\).

Exercise \(\PageIndex{5}\)

Let \(h(t)=\left(\sin (2 \pi t), \cos (2 \pi t), \frac{t}{2}\right)\) parametrize a circular helix \(H\) in \(\mathbb{R}^3\). Plot \(H\) along with the tangent line at \(h\left(\frac{3}{2}\right)\).

Exercise \(\PageIndex{6}\)

Let \(g(t)=(\cos (\pi t), \sqrt{t}, \sin (\pi t))\) parametrize a curve \(C\) in \(\mathbb{R}^3\). Plot \(C\) along with the tangent line at \(g\left(\frac{1}{4}\right)\).

Exercise \(\PageIndex{7}\)

Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}^{2}\) is defined by \(f(t)=(t, \varphi(t))\), where \(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) is differentiable, and let \(C\) be the curve in \(\mathbb{R}^2\) parametrized by \(f\). Show that the tangent line to \(C\) at \(f(c)\) is the same as the line tangent to the graph of \(\varphi\) at \((c, \varphi(c)\).

Answer

Note that the tangent line to \(C\) at \(f(c)\) is parametrized by

\[ A(t)=\left(1, \varphi^{\prime}(c)\right)(t-c)+(c, \varphi(c))=\left(t, \varphi^{\prime}(c)(t-c)+\varphi(c)\right) \nonumber \]

Exercise \(\PageIndex{8}\)

Let \(C\) be the curve in \(\mathbb{R}^2\) parametrized by \(f(t)=\left(t^{3}, t^{6}\right),-\infty<t<\infty .\) Is \(f\) a smooth parametrization of \(C\)? If not, can you find a smooth parametrization of \(C\)?

Answer

No, \(f\) is not a smooth parametrization of \(C\) since \(D f(0)=(0,0)\). However, \(g(t)=\left(t, t^{2}\right),-\infty<t<\infty\), is a smooth parametrization of \(C\).

Exercise \(\PageIndex{9}\)

Let \(C\) be the curve in \(\mathbb{R}^2\) parametrized by \(f(t)=\left(t^{2}, t^{2}\right),-\infty<t<\infty\). Show that \(f\) is not a smooth parametrization of \(C\). Where is the problem? Plot \(C\) and identify the location of the problem.

Answer

\(f\) is not a smooth parametrization of \(C\) since \(D f(0)=(0,0)\).

Exercise \(\PageIndex{10}\)

Let \(\mathbf{v} \neq \mathbf{0}\) and \(\mathbf{p}\) be vectors in \(\mathbb{R}^n\) and let \(C\) be the curve in \(\mathbb{R}^n\) parametrized by \(f(t)=t \mathbf{v}+\mathbf{p}\). What is the best affine approximation to \(f\) at \(t=t_{0}\)?

Exercise \(\PageIndex{11}\)

For each of the following, find the unit tangent vector and the principal unit normal vector at the indicated point.

(a) \(f(t)=\left(t, t^{2}\right), t=1\)

(b) \(g(t)=(3 \sin (2 t), 3 \cos (2 t)), t=\frac{\pi}{3}\)

(c) \(f(t)=(2 \cos (t), 4 \sin (t)), t=\frac{\pi}{4}\)

(d) \(h(t)=(\cos (\pi t), 2 \sin (\pi t)), t=\frac{3}{4}\)

(e) \(g(t)=(\cos (t), \sin (t), t), t=\frac{\pi}{3}\)

(f) \(f(t)=(2 \sin (t), 3 \cos (2 t), 2 t), t=\frac{\pi}{4}\)

(g) \(f(t)=(\sin (\pi t),-\cos (\pi t), 3 t), t=\frac{1}{2}\)

(h) \(g(t)=\left(\cos \left(\pi t^{2}\right), \sin \left(\pi t^{2}\right), t^{2}\right), t=1\)

(i) \(f(t)=\left(t, t^{2}, t^{3}\right), t=2\)

Answer

(a) \(T(1)=\frac{1}{\sqrt{5}}(1,2) ; N(1)=\frac{1}{\sqrt{5}}(-2,1)\)

(c) \(T\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{5}}(-1,2) ; N\left(\frac{\pi}{4}\right)=-\frac{1}{\sqrt{5}}(2,1)\)

(e) \(T\left(\frac{\pi}{3}\right)=\left(-\frac{1}{2} \sqrt{\frac{3}{2}}, \frac{1}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}\right) ; N\left(\frac{\pi}{3}\right)=\left(-\frac{1}{2},-\frac{\sqrt{3}}{2}, 0\right)\)

(g) \(T\left(\frac{1}{2}\right)=\left(0, \frac{\pi}{\sqrt{9+\pi^{2}}}, \frac{3}{\sqrt{9+\pi^{2}}}\right) ; N\left(\frac{1}{2}\right)=(-1,0,0)\)

(i) \(T(2)=\frac{1}{\sqrt{161}}(1,4,12) ; N(2)=\frac{1}{\sqrt{29141}}(-76,-143,54)\)

Exercise \(\PageIndex{12}\)

Use the fact that \(f(t)=(b \cos (t), b \sin (t))\) parametrizes a circle of radius \(b\) to show that a radius of a circle is always perpendicular to the tangent line at the point where the radius touches the circle.

Exercise \(\PageIndex{13}\)

Verify (2.2.21); that is, show that if \(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) and \(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) are both differentiable, then

\[D(\varphi(t) f(t))=\varphi(t) D f(t)+\varphi^{\prime}(t) f(t). \nonumber \]

Exercise \(\PageIndex{14}\)

Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}^{3}\) and \(g: \mathbb{R} \rightarrow \mathbb{R}^{3}\) are both differentiable. Show that

\[ D(f(t) \times g(t))=f(t) \times D g(t)+D f(t) \times g(t), \nonumber \]

yet another version of the product rule.

Exercise \(\PageIndex{15}\)

The following figure illustrates a curve in R² parametrized by some function \(f: \mathbb{R} \rightarrow \mathbb{R}^{2}\). If \(\mathbf{T}\) is the unit tangent vector at the indicated point on the curve, then either \(\mathbf{M}\) or \(\mathbf{N}\) is the principal unit normal vector at that point. Which one is it?

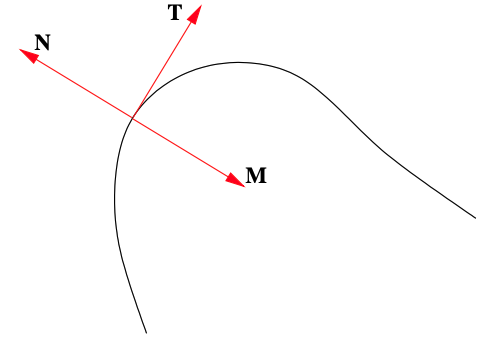
Answer

\(M\)