2.3.E: Motion Along a Curve (Exercises)

Exercise \(\PageIndex{1}\)

For each of the following, suppose a particle is moving along a curve so that its position at time \(t\) is given by \(\mathbf{x}=f(t)\). Find the velocity and acceleration of the particle.

(a) \(f(t)=\left(t^{2}+3, \sin (t)\right)\)

(b) \(f(t)=\left(t^{2} e^{-2 t}, t^{3} e^{-2 t}, 3 t\right)\)

(c) \(f(t)=\left(\cos \left(3 t^{2}\right), \sin \left(3 t^{2}\right)\right)\)

(d) \(f(t)=\left(t \cos \left(t^{2}\right), t \sin \left(t^{2}\right), 3 t \cos \left(t^{2}\right)\right)\)

Answer

(a) \(\mathbf{v}=(2 t, \cos (t)) ; \mathbf{a}=(2,-\sin (t)\)

(c) \(\mathbf{v}=\left(-6 t \sin \left(3 t^{2}\right), 6 t \cos \left(3 t^{2}\right)\right)\); \(\mathbf{a}=\left(-36 t^{2} \cos \left(3 t^{2}\right)-6 \sin \left(3 t^{2}\right),-36 t^{2} \sin \left(3 t^{2}\right)+6 \cos \left(3 t^{2}\right)\right)\)

Exercise \(\PageIndex{2}\)

Find the curvature of the following curves at the given point.

(a) \(f(t)=\left(t, t^{2}\right), t=1\)

(b) \(f(t)=(3 \cos (t), \sin (t)), t=\frac{\pi}{4}\)

(c) \(f(t)=(\cos (t), \sin (t), t), t=\frac{\pi}{3}\)

(d) \(f(t)=\left(\cos (t), \sin (t), e^{-t}\right), t=0\)

Answer

(a) \(\frac{2}{5 \sqrt{5}}\)

(c) \(\frac{1}{2}\)

Exercise \(\PageIndex{3}\)

Plot the curvature for each of the following curves over the given interval \(I\).

(a) \(f(t)=\left(t, t^{2}\right), I=[-2,2]\)

(b) \(f(t)=(\cos (t), 3 \sin (t)), I=[0,2 \pi]\)

(c) \(g(t)=((1+2 \cos (t)) \cos (t),(1+2 \cos (t)) \sin (t)), I=[0,2 \pi]\)

(d) \(h(t)=(2 \cos (t), \sin (t), 2 t), I=[0,2 \pi] \)

(e) \(f(t)=(4 \cos (t)+\sin (4 t), 4 \sin (t)+\sin (4 t)), I=[0,2 \pi]\)

Exercise \(\PageIndex{4}\)

For each of the following, suppose a particle is moving along a curve so that its position at time \(t\) is given by \(\mathbf{x}=f(t)\). Find the coordinates of acceleration in the direction of the unit tangent vector and in the direction of the principal unit normal vector at the specified point. Write the acceleration as a sum of scalar multiples of the unit tangent vector and the principal unit normal vector.

(a) \(f(t)=(\sin (t), \cos (t)), t=\frac{\pi}{3}\)

(b) \(f(t)=(\cos (t), 3 \sin (t)), t=\frac{\pi}{4}\)

(c) \(f(t)=\left(t, t^{2}\right), t=1\)

(d) \(f(t)=(\sin (t), \cos (t), t), t=\frac{\pi}{3}\)

Answer

(a) \(a_{T}=0 ; a_{N}=1 ; a\left(\frac{\pi}{3}\right)=N\left(\frac{\pi}{3}\right)\)

(c) \(a_{T}=\frac{4}{\sqrt{5}} ; a_{N}=\frac{2}{\sqrt{5}} ; a(1)=\frac{4}{\sqrt{5}} T(1)+\frac{2}{\sqrt{5}} N(1)\)

Exercise \(\PageIndex{5}\)

Suppose a particle moves along a curve \(C\) in \(\mathbb{R}^{3}\) so that its position at time \(t\) is given by \(\mathbf{x}=f(t)\). Let \(\mathbf{v}\), \(s\), and \(\mathbf{a}\) denote the velocity, speed, and acceleration of the particle, respectively, and let \(\boldsymbol{\kappa}\) be the curvature of \(C\).

(a) Using the facts \(\mathbf{v}=s T(t)\) and

\[ \mathbf{a}=\frac{d s}{d t} T(t)+s^{2} \kappa N(t) , \nonumber \]

show that \[ \mathbf{v} \times \mathbf{a}=s^{3} \kappa(T(t) \times N(t)) . \nonumber \]

(b) Use the result of part (a) to show that

\[ \kappa=\frac{\|\mathbf{v} \times \mathbf{a}\|}{\|\mathbf{v}\|^{3}}. \nonumber \]

Exercise \(\PageIndex{6}\)

Let \(H\) be the helix in \(\mathbb{R}^{3}\) parametrized by \(f(t)=(\cos (t), \sin (t), t)\). Use the result from Exercise 5 to compute the curvature \(\boldsymbol{\kappa}\) of \(H\) for any time \(t\).

Answer

\( \frac{1}{2}\)

Exercise \(\PageIndex{7}\)

Let \(C\) be the elliptical helix in \(\mathbb{R}^{3}\) parametrized by \(f(t)=(4 \cos (t), 2 \sin (t), t)\). Use the result from Exercise 5 to compute the curvature \(\boldsymbol{\kappa}\) of \(C\) at \(t=\frac{\pi}{4}\)

Answer

\(\frac{\sqrt{74}}{11 \sqrt{11}}\)

Exercise \(\PageIndex{8}\)

Let \(C\) be the curve in \(\mathbb{R}^{2}\) which is the graph of the function \(\varphi: \mathbb{R} \rightarrow \mathbb{R}\). Use the result from Exercise 5 to show that the curvature of \(C\) at the point \((t, \varphi(t))\) is

\[\kappa=\frac{\left|\varphi^{\prime \prime}(t)\right|}{\left(1+\left(\varphi^{\prime}(t)\right)^{2}\right)^{\frac{3}{2}}} . \nonumber \]

Exercise \(\PageIndex{9}\)

Let \(P\) be the graph of \(f(t)=t^{2}\). Use the result from Exercise 8 to find the curvature of \(P\) at (1,1) and (2,4).

Answer

\(\frac{2}{5 \sqrt{5}}\) and \(\frac{2}{17 \sqrt{17}}\)

Exercise \(\PageIndex{10}\)

Let \(C\) be the graph of \(f(t)=t^{3}\). Use the result from Exercise 8 to find the curvature of \(C\) at (1,1) and (2,8).

Exercise \(\PageIndex{11}\)

Let \(C\) be the graph of \(g(t)=\sin (t)\). Use the result from Exercise 8 to find the curvature of \(C\) at \(\left(\frac{\pi}{2}, 1\right)\) and \(\left(\frac{\pi}{4}, \frac{1}{\sqrt{2}}\right)\).

Answer

1 and \(\frac{2}{3 \sqrt{3}}\)

Exercise \(\PageIndex{12}\)

For each of the following, suppose a particle is moving along a curve so that its positionat time \(t\) is given by \(\mathbf{x}=f(t)\). Find the distance traveled by the particle over the given time interval.

(a) \(f(t)=(\sin (t), 3 \cos (t)), I=[0,2 \pi]\)

(b) \(f(t)=(\cos (\pi t), \sin (\pi t), 2 t), I=[0,4]\)

(c) \(f(t)=\left(t, t^{2}\right), I=[0,2]\)

(d) \(f(t)=(t \cos (t), t \sin (t)), I=[0,2 \pi]\)

(e) \(f(t)=\left(\cos (2 \pi t), \sin (2 \pi t), 3 t^{2}, t\right), I=[0,1]\)

(f) \(f(t)=\left(e^{-t} \cos (\pi t), e^{-t} \sin (\pi t)\right), I=[-2,2]\)

(g) \(f(t)=(4 \cos (t)+\sin (4 t), 4 \sin (t)+\sin (4 t)), I=[0,2 \pi]\)

Answer

(a) \(13.3649\)

(c) \(\sqrt{17}+\frac{1}{4} \sinh ^{-1}(4) \approx 4.64678\)

(e) \(\frac{1}{2} \sqrt{37+4 \pi^{2}}+\frac{1}{12}\left(1+4 \pi^{2}\right) \sinh ^{-1}\left(\frac{6}{\sqrt{1+4 \pi^{2}}}\right) \approx 7.20788\)

(g) \(32.2744\)

Exercise \(\PageIndex{13}\)

Verify that the circumference of a circle of radius \(r\) is \(2\pi r\).

Exercise \(\PageIndex{14}\)

The curve parametrized by

\[ f(t)=(\sin (2 t) \cos (t), \sin (2 t) \sin (t)) \nonumber \]

has four “petals.” Find the length of one of these petals.

Answer

2.4221

Exercise \(\PageIndex{15}\)

The curve \(C\) parametrized by \(h(t)=\left(\cos ^{3}(t), \sin ^{3}(t)\right)\) is called a hypocycloid (see Figure 2.2.3 in Section 2.2). Find the length of \(C\).

Answer

6

Exercise \(\PageIndex{16}\)

Suppose \(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) is continuously differentiable and let \(C\) be the part of the graph of \(\varphi\) over the interval \([a,b]\). Show that the length of \(C\) is

\[ \int_{a}^{b} \sqrt{1+\left(\varphi^{\prime}(t)\right)^{2}} d t . \nonumber \]

Exercise \(\PageIndex{17}\)

Use the result from Exercise 16 to find the length of one arch of the graph of \(f(t)= \sin (t)\).

Answer

3.8202

Exercise \(\PageIndex{18}\)

Let \(h: \mathbb{R} \rightarrow \mathbb{R}^{n}\) parametrize a curve \(C\). We say \(C\) is parametrized by arc length if \(\|D h(t)\|=1\) for all \(t\).

(a) Let \(\sigma\) be the arc length function for \(C\) using the parametrization \(f\) and let \(\sigma^{-1}\) be its inverse function. Show that the function \(g: \mathbb{R} \rightarrow \mathbb{R}^{n}\) defined by \(g(u)=f\left(\sigma^{-1}(u)\right)\) parametrizes \(C\) by arc length.

(b) Let \(C\) be the circular helix in \(\mathbb{R}^{3}\) with parametrization \(f(t)=(\cos (t), \sin (t), t)\). Find a function \(g: \mathbb{R} \rightarrow \mathbb{R}^{n}\) which parametrizes \(C\) by arc length.

Exercise \(\PageIndex{19}\)

Suppose \(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) is continuous on the closed interval \([a,b]\) and has coordinate functions \(f_{1}, f_{2}, \ldots, f_{n}\). We define the definite integral of f over the interval \([a,b]\) to be

\[ \int_{a}^{b} f(t) d t=\left(\int_{a}^{b} f_{1}(t) d t, \int_{a}^{b} f_{2}(t) d t, \ldots, \int_{a}^{b} f_{n}(t) d t\right) . \nonumber \]

Show that if a particle moves so its velocity at time \(t\) is \(\mathbf{v}(t)\), then, assuming \(\mathbf{v}\) is a continuous function on an interval \([a,b]\), the position of the particle for any time \(t\) in \([a,b]\) is given by

\[ \mathbf{x}(t)=\int_{a}^{t} \mathbf{v}(s) d s+\mathbf{x}(a) . \nonumber \]

Exercise \(\PageIndex{20}\)

Suppose a particle moves along a curve in \(\mathbb{R}^{3}\) so that its velocity at any time \(t\) is

\[ \mathbf{v}(t)=(\cos (2 t), \sin (2 t), 3 t) . \nonumber \]

If the particle is at (0,1,0) when \(t=0\), use Exercise 19 to determine its position for any other time \(t\).

Answer

\(\mathbf{x}(t)=\left(\frac{1}{2} \sin (2 t), \frac{3}{2}-\frac{1}{2} \cos (2 t), \frac{3}{2} t^{2}\right)\)

Exercise \(\PageIndex{21}\)

Suppose a particle moves along a curve in \(\mathbb{R}^{3}\) so that its acceleration at any time \(t\) is

\[ \mathbf{a}(t)=(\cos (t), \sin (t), 0) .\nonumber \]

If the particle is at (1,2,0) with velocity (0,1,1) at time \(t=0\), use Exercise 19 to determine its position for any other time \(t\).

Answer

\(\mathbf{x}(t)=(2-\cos (t), 2+2 t-\sin (2 t), t)\)

Exercise \(\PageIndex{22}\)

Suppose a projectile is fired from the ground at an angle \(\alpha\) with an initial speed \(v_0\), as shown in Figure 2.3.5. Let \(\mathbf{x}(t)\), \(\mathbf{v}(t)\), and \(\mathbf{a}(t)\) be the position, velocity, and acceleration, respectively, of the projectile at time \(t\).

Figure \(\PageIndex{5}\): The path of a projectile

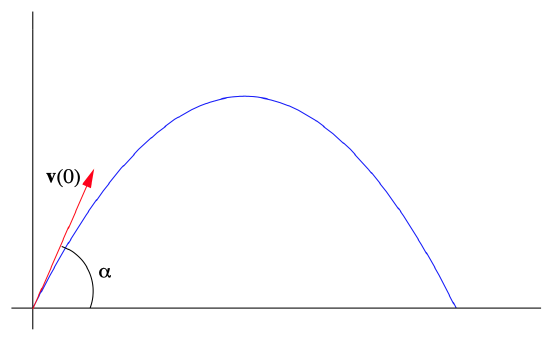
(a) Explain why \(\mathbf{x}(0)=(0,0)\), \(\mathbf{v}(0)=\left(v_{0} \cos (\alpha), v_{0} \sin (\alpha)\right)\), and \(\mathbf{a}(t)=(0,-g)\) for all \(t\), where \(g=9.8\) meters per second per second is the acceleration due to gravity.

(b) Use Exercise 19 to find \(\mathbf{v}(t)\).

(c) Use Exercise 19 to find \(\mathbf{x}(t)\).

(d) Show that the curve parametrized by \(\mathbf{x}(t)\) is a parabola. That is, let \(\mathbf{x}(t)=(x, y)\) and show that \(y=a x^{2}+b x+c\) for some constants \(a\), \(b\), and \(c\).

(e) Show that the range of the projectile, that is, the horizontal distance traveled, is

\[ R=\frac{v_{0} \sin (2 \alpha)}{g} \nonumber \]

and conclude that the range is maximized when \(\alpha=\frac{\pi}{4}\)

(f) When does the projectile hit the ground?

(g) What is the maximum height reached by the projectile? When does it reach this height?

Exercise \(\PageIndex{23}\)

Suppose \(\mathbf{a}_{1}, \mathbf{a}_{2}, \ldots, \mathbf{a}_{m}\) are unit vectors in \(\mathbb{R}^{n}\), \(m \leq n,\) which are mutually orthogonal (that is, \(a_{i} \perp a_{j}\) when \(i \neq j\)). If \(\mathbf{x}\) is a vector in \(\mathbb{R}^{n}\) with

\[ \mathbf{x}=x_{1} \mathbf{a}_{1}+x_{2} \mathbf{a}_{2}+\cdots+x_{m} \mathbf{a}_{m} , \nonumber \]

show that \(x_{i}=\mathbf{x} \cdot \mathbf{a}_{i}, i=1,2, \ldots, m\).