2.6: Exercises

Last updated
Save as PDF

Page ID: 60305

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Exercise $\PageIndex{1}$

Apply the division algorithm to the following number pairs. (Hint: replace negative numbers by positive ones.)

$110, 7$.
$51, -30$.
$-138, 24$.
$272, 119$.
$2378, 1769$.
$270, 175560$.

Exercise $\PageIndex{2}$

In this exercise we will exhibit the division algorithm applied to polynomials $x+1$ and $3x^3+2x+1$ with coefficients in $\mathbb{Q}, \mathbb{R}$, or $\mathbb{C}$.

Apply long division to divide $3021$ by $11$. (Hint: $3021 = 11 \cdot 275 -4$.)
Apply the exact same algorithm to divide $3x^3+2x+1$ by $x+1$. In this algorithm, $x^k$ behaves as $10^k$ in (a). (Hint: every step, cancel the highest power of $x$.)
Verify that you obtain $3x^3+2x+1 = (x+1)(3x^2-3x+5)-4$.
Show that in general, if $p_{1}$ and $p_{2}$ are polynomials such that the degree of $p_{1}$ is greater or equal to the degree of $p_{2}$, then $p_{1} = q_{2}p_{2}+p_{3}$, where the degree of $p_{3}$ is less than the degree of $p_{2}$. (Hint: perform long division as in (b). Stop when the degree of the remainder is less than that of $p_{2}$.)
Why does this division not work for polynomials with coefficients in $\mathbb{Z}$? (Hint: replace $x+1$ by $2x+1$.)

Exercise $\PageIndex{3}$
Compute by long division that $3021 = 11 \cdot 274+7$.
Conclude from exercise 2.2 that $3021 = 11(300-30+5)-4$. (Hint: let $x = 10$.)
Conclude from exercise 2.2 that $3 \cdot 163 +2 \cdot 16+1 = 17(3 \cdot 162-3 \cdot 16+5)-4$. (Hint: let $x = 16$.)

Exercise $\PageIndex{4}$

Use unique factorization to show that any composite number $n$ must have a prime factor less than or equal to $\sqrt{n}$.
Use that fact to prove: If we apply Eratosthenes’ sieve to $\{2, 3, \cdots, n\}$, it is sufficient to sieve out numbers less than or equal to $\sqrt{n}$.

Exercise $\PageIndex{5}$

We give an elementary proof of Corollary 2.15.

Show that $a \cdot \frac{b}{\gcd (a,b)}$ is a multiple of $a$.
Show that $\frac{b}{\gcd (a,b)} \cdot b$ is a multiple of $b$.
Conclude that $\frac{ab}{\gcd (a,b)}$ is a multiple of both $a$ and $b$ and thus greater than or equal to $\mbox{lcm} (a,b)$.
Show that $a/(\frac{ab}{\mbox{lcm} (a,b)}) = \frac{\mbox{lcm} (a,b)}{b}$ is an integer. Thus $\frac{ab}{\mbox{lcm} (a,b)}$ is a divisor of $a$.
Similarly, show that $\frac{ab}{\mbox{lcm} (a,b)}$ is a divisor of $b$.
Conclude that $\frac{ab}{\mbox{lcm} (a,b)} \le \gcd (a,b)$.
Finish the proof.

Exercise $\PageIndex{6}$

It is possible to extend the definition of $\gcd$ and $\mbox{lcm}$ to more than two integers (not all of which are zero). For example $\gcd (24, 27, 54) = 3$.

Compute $\gcd (6,10,15)$ and $\mbox{lcm} (6,10,15)$.
Give an example of a triple whose $\gcd$ is one, but every pair of which has a $\gcd$ greater than one.
Show that there is no triple $\{a,b,c\}$ whose $\mbox{lcm}$ equals $abc$, but every pair of which has lcm less than the product of that pair. (Hint: consider $\mbox{lcm} (a \cdot b) \cdot c$.)

Exercise $\PageIndex{7}$

Give the prime factorization of the following numbers: $12, 392, 1043, 31, 128, 2160, 487$.
Give the prime factorization of the following numbers: $12 \cdot 392, 1043 \cdot 31, 128 \cdot 2160$.
Give the prime factorization of: $1, 250000, 63^3, 720$, and the product of the last three numbers.

Exercise $\PageIndex{8}$

Use the Fundamental Theorem of Arithmetic to prove:

Be ́zout’s Lemma.
Euclid’s Lemma.

Exercise $\PageIndex{9}$

For positive integers $m$ and $n$, suppose that $m^{\alpha} = n$. Show that $\alpha = \frac{p}{q}$ with $\gcd(p,q) = 1$ if and only if

\[\begin{array}{ccccc} {m = \prod_{i=1}^{s} p_{i}^{k_{i}}}&{and}&{n = \prod_{i=1}^{s} p_{i}^{l_{i}}}&{with}&{\forall i pk_{i} = ql_{i}} \end{array} \nonumber\]

Exercise $\PageIndex{10}$

We develop the proof of Theorem 2.16 as it was given by Euler. We start by assuming that there is a finite list $L$ of $k$ primes. We will show in the following steps how that assumption leads to a contradiction. We order the list according to ascending order of magnitude of the primes. So $L = \{p_{1}, p_{2}, \cdots, p_{k}\}$ where $p_{1} = 2, p_{2} = 3, p_{3} = 5$, and so forth, upto the last prime $p_{k}$.

Show that $\prod_{i=1}^{k} \frac{p_{i}}{p_{i}-1}$ is finite, say $M$.
Show that for $r > 0$, \[\prod_{i=1}^{k} \frac{p_{i}}{p_{i}-1} = \prod_{i=1}^{k} \frac{1}{1-p_{i}^{-1}} > \prod_{i=1}^{k} \frac{1-p_{i}^{-r-1}}{1-p_{i}^{-1}} = \prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) \nonumber\]
Use the fundamental theorem of arithmetic to show that there is an $\alpha (r) > 0$ such that \[\prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) = \sum_{l=1}^{\alpha (r)} \frac{1}{l}+R \nonumber\], where $R$ is a non-negative remainder.
Show that for all $K$ there is an $r$ such that $\alpha (r) > K$.
Thus for any $K$, there is an $r$ such that \[\prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) \ge \sum_{l=1}^{K} \frac{1}{l} \nonumber\]
Conclude with a contradiction between a) and e). (Hint: the harmonic series $\sum \frac{1}{l}$ diverges or see exercise 2.11 c).)

Exercise $\PageIndex{11}$

In this exercise we consider the Riemann zeta function for real values of $s$ greater than $1$.

Show that for all $x > -1$, we have $\mbox{ln} (1+x) \le x$.
Use Proposition 2.20 and a) to show that \[\mbox{ln} \zeta (s) \le \sum_{\mbox{p prime}} \frac{p^{-s}}{1-p^{-s}} \le \sum_{\mbox{p prime}} \frac{p^{-s}}{1-2^{-s}} \nonumber\]
Use the following argument to show that $\lim_{s \rightarrow 1} \zeta (s) = \infty$. \[\sum_{n=1}^{\infty} n^{-1} \ge \sum_{n=1}^{\infty} n^{-s} \ge \int_{1}^{\infty} x^{-s} dx \nonumber\] (For the last inequality, see Figure 4.)
Show that b) and c) imply that $\sum_{\mbox{p prime}} p^{-s}$ diverges as $s \rightarrow 1$.
Show that – in some sense – primes are more frequent than squares in the natural numbers. (Hint: $\sum_{n=1}^{\infty} n^{-2}$ converges.)

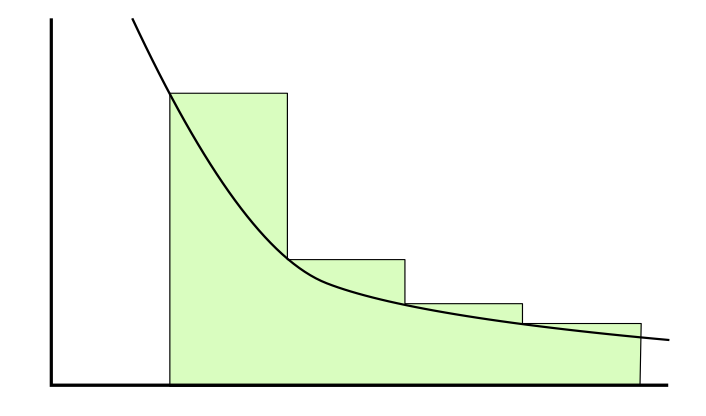
$Screen Shot 2021-04-08 at 10.43.50 PM.png$

Figure 4. Proof that $\sum_{n=1}^{\infty} f(n)$ is greater than $\int_{1}^{\infty} x^{-s} dx$ if $f$ is positive and decreasing.

Exercise $\PageIndex{12}$

Let $E$ be the set of even numbers. Let $a, c$ in $E$, then $c$ is divisible by $a$ if there is $ab \in E$ so that $ab = c$. Define a prime $p$ in $E$ as a number in $E$ such that there are no $a$ and $b$ in $E$ with $ab = p$.

List the first $30$ primes in $E$.
Does Euclid’s lemma hold in $E$? Explain.
Factor 60 into primes (in $E$) in two different ways.

Exercise $\PageIndex{13}$

See exercise 2.12. Show that any number in $E$ is a product of primes in $E$. (Hint: follow the proof of Theorem 2.14, part (1).)

Exercise $\PageIndex{14}$

See exercise 2.12 which shows that unique factorization does not hold in $E = \{2, 4, 6, \dots\}$. The proof of unique factorization uses Euclid’s lemma. In turn, Euclid’s lemma was a corollary of Be ́zout’s lemma, which depends on the division algorithm. Where exactly does the chain break down in this case?

Exercise $\PageIndex{15}$

Let $L = \{p_{1}, p_{2}, \cdots\}$ be the list of all primes, ordered according ascending magnitude. Show that $p_{n+1} \le \prod_{i=1}^{n} p_{i}$. (Hint: consider $d$ as in the proof of Theorem 2.16, let $p_{n+1}$ be the smallest prime divisor of $d-1$.)

A much stronger version of exercise 2.15 is the so-called Bertrand’s Postulate. That theorem says that for every $n \ge 1$, there is a prime in $\{n+1, \dots, 2n\}$. It was proved by Chebyshev. Subsequently the proof was simplified by Ramanujan and Erdo ̈s [18].

Exercise $\PageIndex{16}$

Let $p$ and $q$ primes greater than or equal to $5$.

Show that $p = 12q+r$ where $r \in \{1,5,7,11\}$. (The same holds for $q$.)
Show that $24|p^2-q^2$. (Hint: use (a) to reduce this to ${4 \choose 2} = 6$ cases.)

Exercise $\PageIndex{17}$

A square full number is a number $n > 1$ such that each prime factor occurs with a power at least $2$. A square free number is a number $n > 1$ such that each prime factor occurs with a power at most $1$.

If $n$ is square full, show that there are positive integers $a) and \(b$ such that $n = a^{2}b^{3}$.
Show that every integer greater than one is the product of a square free number and a square number.

Exercise $\PageIndex{18}$

Let $L = \{p_{1}, p_{2},\dots\}$ be the list of all primes, ordered ac- cording ascending magnitude. The numbers $E_{n} = 1 + \prod_{i=1}^{n} p_{i}$ are called Euclid numbers.

Check the primality of $E_{1}$ through $E_{6}$.
Show that $E_{n} = _{4} 3\_. (Hint: \(E_{n}-1$ is twice an odd number.)
Show that for $n \le 3$ the decimal representation of $E_{n}$ ends in a $1$. (Hint: look at the factors of $E_{n}$.)

Exercise $\PageIndex{19}$

Twin primes are a pair of primes of the form $p$ and $p+2$.

Show that the product of two twin primes plus one is a square.
Show that $p > 3$, the sum of twin primes is divisible by $12$. (Hint: see exercise 2.16)

Exercise $\PageIndex{20}$

Show that there arbitrarily large gaps between successive primes. More precisely, show that every integer in $\{n!+2, n!+3, \dots n!+n\}$ is composite.

The usual statement for the fundamental theorem of arithmetic includes only natural numbers $n \in \mathbb{N}$ (i.e. not $\mathbb{Z}$) and the common proof uses induction on n. We review that proof in the next two problems.

Exercise $\PageIndex{21}$

Prove that $2$ can be written as a product of primes.
Let $k > 2$. Suppose all numbers in $\{1, 2, \dots k\}$ can be written as a product of primes (or $1$). Show that $k+1$ is either prime or composite.
If in (b), $k+1$ is prime, then all numbers in $\{1, 2, \dots k+1\}$ can be written as a product of primes (or $1$).
If in (b), $k+1$ is composite, then there is a divisor $d \in \{2,\dots k\}$ such that $k+1 = dd'$.
Show that the hypothesis in (b) implies also in this case, all numbers in $\{1, 2, \dots k+1\}$ can be written as a product of primes (or $1$).
Use the above to formulate the inductive proof that all elements of $\mathbb{N}$ can be written as a product of primes.

Exercise $\PageIndex{22}$

The set-up of the proof is the same as in exercise 2.21. Use induction on $n$. We assume the result of that exercise.

Show that $n = 2$ has a unique factorization.
Suppose that if for $k > 2, \{2, \dots k\}$ can be uniquely factored. Then there are primes $p_{i}$ and $q_{i}$, not necessarily distinct, such that \[k+1 = \prod_{i=1}^{s} p_{i} = \prod_{i=1}^{r} q_{i} \nonumber\]
Show that then $p_{1}$ divides $\prod_{i=1}^{r} q_{i}$ and so, Corollary 2.12 implies that there is a $j \le r$ such that $p_{1} = q_{j}$.
Relabel the $q_{i}'$s, so that $p_{1} = q_{1}$ and divide $n$ by $p_{1} = q_{1}$. Show that \[\frac{k+1}{q_{1}} = \prod_{i=2}^{s} p_{i} = \prod_{i=2}^{r} q_{i} \nonumber\]
Show that the hypothesis in (b) implies that the remaining $p_{i}$ equal the remaining $q_{i}$. (Hint: $\frac{k}{q_{1}} \le k$.)
Use the above to formulate the inductive proof that all elements of $\mathbb{N}$ can be uniquely factored as a product of primes.

Here is a different characterization of gcd and lcm. We prove it as a corollary of the prime factorization theorem.

Corollary 2.23

A common divisor $d > 0$ of $a$ and $b$ equals $\gcd(a, b)$ if and only if every common divisor of $a$ and $b$ is a divisor of $d$.
Also, a common multiple $d > 0$ of $a$ and $b$ equals $\mbox{lcm} (a, b)$ if and only if every common multiple of $a$ and $b$ is a multiple of $d$.

Exercise $\PageIndex{23}$

Use the characterization of $\gcd(a, b)$ and $\mbox{lcm} (a,b)$ given in the proof of Corollary 2.15 to prove Corollary 2.23.

Exercise $\PageIndex{24}$

Let $p$ be a fixed prime. Show that the probability that two independently chosen integers in $\{1,2,\cdots,n\}$ are divisible by $p$ tends to $\frac{1}{p^2}$ as $n \rightarrow \infty$. Equivalently, the probability that they are not divisible by $p$ tends to $1-\frac{1}{p^2}$.
Make the necessary assumptions, and show that the probability that two independently chosen integers in $\{1,2,\cdots,n\}$ are not divisible by any prime tends to $\prod_{p prime} (1-p^{-2})$. (Hint: you need to assume that the probabilities in 1. are independent and so they can be multiplied.)
Show that from 2. and Euler's product formula, it follows that for 2 random (positive) integers $a$ and $b$ to have $\gcd (a,b) = 1$ has probability $1/\zeta (2) \approx 0.61$
Show that $d >1$ integers $\{a_{1}, a_{2}, \cdots, a_{d}\}$ that probability equals $1/\zeta(d)$. (Hint: the reasoning is the same as in 1., 2., 3.)
Show that for $d \ge 2$: \[1 < \zeta (d) < 1+\int_{1}^{\infty} x^{-d} dx \nonumber\] For the last inequality, see Figure 5.
Show that for large $d$, the probability that $\gcd (a_{1},a_{2},\cdots,a_{d}) = 1$ tends to $1$.

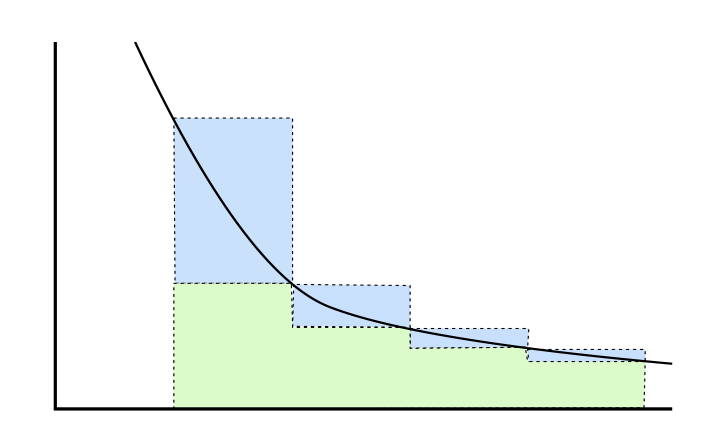
$Screen Shot 2021-04-16 at 4.31.15 PM.png$

Figure 5. Proof that $\sum_{n=1}^{\infty} f(n)$ (shaded) minus $f(1)$ (shaded in blue) is less than $\int_{1}^{\infty} x^{-s} dx$ is positive and decreasing.

Exercise $\PageIndex{25}$

This exercise in based on exercise 2.24.

In the $\{-4,\cdots, 4\}^2 \backslash (0,0)$ grid in $\mathbb{Z}^{2}$, find out which propotion of the lattice points is visible from the origin, see Figure 6.
Show that in a large grid, this propotion tends to $1/\zeta (2)$.
Show that as the dimension increases to infinity, the propotion of the lattice points $\mathbb{Z}^{d}$ that are visible from the origin, increases to 1.

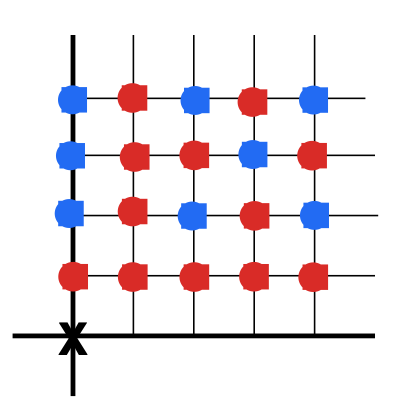
$Screen Shot 2021-04-16 at 4.36.53 PM.png$

Figure 6. The origin is marked by “$\times$”. The red dots are visible from $\times$; between any blue dot and $\times$ there is a red dot. The picture shows exactly one quarter of $\{-4,\cdots ,4\}^{2} \backslash (0,0) \subset \mathbb{Z}^2$.