15.1: Cyclic Groups
( \newcommand{\kernel}{\mathrm{null}\,}\)
Groups are classified according to their size and structure. A group's structure is revealed by a study of its subgroups and other properties (e.g., whether it is abelian) that might give an overview of it. Cyclic groups have the simplest structure of all groups.
Definition
Group
Example
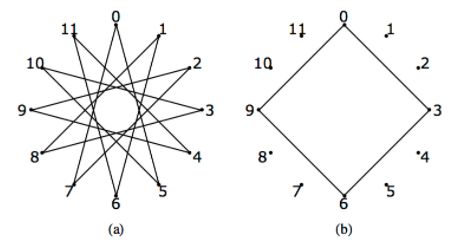 Figure
Figure Figure
Example
The additive group of integers,
This observation does not mean that every integer is the product of an integer times 1. It means that
Theorem
If
- Proof
-
Let
One of the first steps in proving a property of cyclic groups is to use the fact that there exists a generator. Then every element of the group can be expressed as some multiple of the generator. Take special note of how this is used in theorems of this section.
Up to now we have used only additive notation to discuss cyclic groups. Theorem
Example
The group of positive integers modulo 11 with modulo 11 multiplication,
Example
The real numbers with addition,
 Figure
Figure The next two proofs make use of the Theorem 11.4.1.
The following theorem shows that a cyclic group can never be very complicated.
Theorem
If
- Proof
-
Case 1:
Since
Therefore
Case 2:
Theorem
Every subgroup of a cyclic group is cyclic.
- Proof
-
Let
Example
The only proper subgroups of
Example
With the exception of
We now cite a useful theorem for computing the order of cyclic subgroups of a cyclic group:
Theorem
If
- Proof
-
The proof of this theorem is left to the reader.
Example
To compute the order of
At this point, we will introduce the idea of a fast adder, a relatively modern application (Winograd, 1965) of an ancient theorem, the Chinese Remainder Theorem. We will present only an overview of the theory and rely primarily on examples.
Out of necessity, integer addition with a computer is addition modulo
Now we will introduce a hypothetical problem that we will use to illustrate the idea of a fast adder. Suppose that we had to add 1,000 numbers modulo
Theorem
Let
by
where for
The Chinese Remainder Theorem can be stated in several different forms, and its proof can be found in many abstract algebra texts.
As we saw in Chapter 11,
Let's consider a somewhat larger case. We start by selecting a modulus that can be factored into a product of relatively prime integers: x += a is interpreted as the instruction to add the value of a to the variable x.
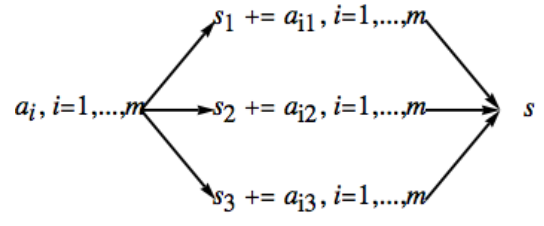 Figure
Figure Assume we have several integers s to compare our result with this true sum.
1 | a=[1878,1384,84,2021,784,1509,1740,1201,2363,1774, |
2 | 1865,33,1477,894,690,520,198,1349,1278,650] |
3 | s =0 |
4 | for t in a: |
5 | s+=t |
6 | s |
Although our sum is an integer calculation, we will put our calculation in the context of the integers modulo 21600. The isomophism from theta. In addition we demonstrate that the operations in these groups are preserved by theta.
1 | G=cartesian_product([Integers(32),Integers(27),Integers(25)]) |
2 | def theta(x): |
3 | return G((x%32,x%27,x%25)) |
4 | [theta(1878)+theta(1384),theta(1878+1384)] |
We initialize the sums in each factor of the range of theta to zero and decompose each summand
1 | sum=G((0,0,0)) |
2 | for t in a: |
3 | sum+=theta(t) |
4 | sum |
Addition in theta is built into most mathematics programs, including Sage. In Sage the function is crt. We use this function to compute the inverse of our triple, which is an element of
1 | isum=crt([12,13,17],[32,27,25]) |
2 | [isum,(s-isum)%(21600)] |
In order to get the true sum from our scheme, the modulus would need to be increased by moving from 21600 to, for example, crt, but adding the summands that are in the form of quadruples can be done with no additional time.
The computation of crt can be accomplished in a variety of ways. All of them ultimately are simplified by the fact that
The inverse images of the “unit vectors” can be computed ahead of time.
1 | u=[crt([1,0,0],[32,27,25]), |
2 | crt([0,1,0],[32,27,25]),crt([0,0,1],[32,27,25])] |
3 | u |
The result we computed earlier can be computed directly by in the larger modulus.
1 | (7425*12 + 6400*13+ 7776* 17)%21600 |
To further illustrate the potential of fast adders, consider increasing the modulus to
Exercises
Exercise
What generators besides 1 does
- Answer
-
The only other generator is
Exercise
Suppose
Exercise
Prove that if
- Answer
-
If
Similarly, if
Exercise
If you wanted to list the generators of
Exercise
Which of the following groups are cyclic? Explain.
- Answer
-
- No. Assume that
- No. Similar reasoning to part a.
- Yes. 6 is a generator of
- No.
- Yes,
- No. Assume that
Exercise
For each group and element, determine the order of the cyclic subgroup generated by the element:
Exercise
How can Theorem
- Answer
-
Theorem
Exercise
Prove that if the greatest common divisor of
Exercise
- Illustrate how the fast adder can be used to add the numbers 21, 5, 7, and 15 using the isomorphism between
- If the same isomorphism is used to add the numbers 25, 26, and 40, what would the result be, why would it be incorrect, and how would the answer differ from the answer in part a?
- Answer
-
The final sum, 48, is obtained by using the facts that
- Using the same isomorphism:
The actual sum is 91. Our result is incorrect, since 91 is not in
Exercise
Prove that if


