15.2: Cosets and Factor Groups

Consider the group $\left[\mathbb{Z}_{12};+_{12}\right]\text{.}$ As we saw in the previous section, we can picture its cyclic properties with the string art of Figure 15.1.1. Here we will be interested in the non-generators, like 3. The solid lines in Figure $\PageIndex{1}$ show that only one-third of the tacks have been reached by starting at zero and jumping to every third tack. The numbers of these tacks correspond to $\langle 3 \rangle = \{0, 3, 6, 9\}\text{.}$

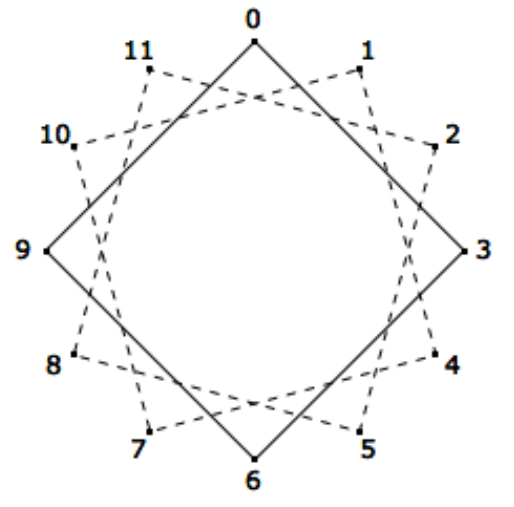Figure $\PageIndex{1}$: "String art" cosets

What happens if you start at one of the unused tacks and again jump to every third tack? The two broken paths on Figure $\PageIndex{1}$ show that identical squares are produced. The tacks are thus partitioned into very similar subsets. The subsets of $\mathbb{Z}_{12}$ that they correspond to are $\{0, 3, 6, 9\}\text{,}$ $\{1, 4, 7, 10\}\text{,}$ and $\{2, 5, 8, 11\}\text{.}$ These subsets are called cosets. In particular, they are called cosets of the subgroup $\{0, 3, 6, 9\}\text{.}$ We will see that under certain conditions, cosets of a subgroup can form a group of their own. Before pursuing this example any further we will examine the general situation.

Definition $\PageIndex{1}$: Coset

If $[G;*]$ is a group, $H \leq G$ and $a \in G\text{,}$ the left coset of $H$ generated by $a$ is

$$\begin{equation*} a*H = \{ a*h | h \in H\} \end{equation*}$$

and the right coset of $H$ generated by $a$ is

$$\begin{equation*} H*a = \{h*a | h\in H\}. \end{equation*}$$

Note $\PageIndex{1}$

1. $H$ itself is both a left and right coset since $e*H = H*e = H\text{.}$
2. If $G$ is abelian, $a*H = H*a$ and the left-right distinction for cosets can be dropped. We will normally use left coset notation in that situation.

Definition $\PageIndex{2}$: Cost Representative

Any element of a coset is called a representative of that coset.

One might wonder whether $a$ is in any way a special representative of $a*H$ since it seems to define the coset. It is not, as we shall see.

Remark $\PageIndex{1}$: A Duality Principle

A duality principle can be formulated concerning cosets because left and right cosets are defined in such similar ways. Any theorem about left and right cosets will yield a second theorem when “left” and “right” are exchanged for “right” and “left.”

Theorem $\PageIndex{1}$

If $b\in a*H\text{,}$ then $a*H = b*H\text{,}$ and if $b \in H*a\text{,}$ then $H*a = H*b\text{.}$

Proof

In light of the remark above, we need only prove the first part of this theorem. Suppose that $x \in a*H\text{.}$ We need only find a way of expressing $x$ as “$b$ times an element of $H\text{.}$” Then we will have proven that $a*H \subseteq b*H\text{.}$ By the definition of $a*H\text{,}$ since $b$ and $x$ are in $a*H\text{,}$ there exist $h_1$ and $h_2$ in $H$ such that $b = a*h_1$ and $x = a*h_2\text{.}$ Given these two equations, $a = b h_1^{-1}$ and

$$\begin{equation*} x = a*h_2 = (b *h_1^{-1})*h_2 = b*(h_1^{-1}*h_2) \end{equation*}$$

Since $h_1,h_2 \in H\text{,}$ $h_1^{-1}*h_2 \in H\text{,}$ and we are done with this part of the proof. In order to show that $b*H \subseteq a*H\text{,}$ one can follow essentially the same steps, which we will let the reader fill in.

Example $\PageIndex{1}$

In Figure $\PageIndex{1}$, you can start at either 1 or 7 and obtain the same path by taking jumps of three tacks in each step. Thus,

$$\begin{equation*} 1+_{12} \{0, 3, 6, 9\} = 7 +_{12} \{0, 3, 6, 9\} = \{1, 4, 7, 10\}. \end{equation*}$$

The set of left (or right) cosets of a subgroup partition a group in a special way:

Theorem $\PageIndex{2}$: Cosets Partition a Group

If $[G; *]$ is a group and $H\leq G\text{,}$ the set of left cosets of $H$ is a partition of $G\text{.}$ In addition, all of the left cosets of $H$ have the same cardinality. The same is true for right cosets.

Proof

That every element of $G$ belongs to a left coset is clear because $a \in a*H$ for all $a \in G\text{.}$ If $a*H$ and $b*H$ are left cosets, we will prove that they are either equal or disjoint. If $a*H$ and $b*H$ are not disjoint, $a*H\cap b*H$ is nonempty and some element $c \in G$ belongs to the intersection. Then by Theorem $\PageIndex{1}$, $c\in a*H \Rightarrow a*H = c*H$ and $c \in b*H \Rightarrow b*H = c*H\text{.}$ Hence $a*H = b*H\text{.}$

We complete the proof by showing that each left coset has the same cardinality as $H\text{.}$ To do this, we simply observe that if $a \in G\text{,}$ $\rho:H \to a*H$ defined by $\rho(h)= a*h$ is a bijection and hence $\lvert H\rvert =\lvert a *H\rvert\text{.}$ We will leave the proof of this statement to the reader.

The function $\rho$ has a nice interpretation in terms of our opening example. If $a \in \mathbb{Z}_{12}\text{,}$ the graph of $\{0, 3, 6, 9\}$ is rotated $(30a)^{\circ}$ to coincide with one of the three cosets of $\{0, 3, 6, 9\}\text{.}$

Corollary $\PageIndex{1}$: A Coset Counting Formula

If $\lvert G\rvert < \infty$ and $H\leq G\text{,}$ the number of distinct left cosets of $H$ equals $\frac{\lvert G\rvert }{\lvert H\rvert }\text{.}$ For this reason we use $G/H$ to denote the set of left cosets of $H$ in $G$

Proof

This follows from the partitioning of $G$ into equal sized sets, one of which is $H\text{.}$

Example $\PageIndex{2}$

The set of integer multiples of four, $4\mathbb{Z}\text{,}$ is a subgroup of $[\mathbb{Z}; +]\text{.}$ Four distinct cosets of $4\mathbb{Z}$ partition the integers. They are $4\mathbb{Z}\text{,}$ $1+4\mathbb{Z}\text{,}$ $2+4\mathbb{Z}\text{,}$ and $3+4\mathbb{Z}\text{,}$ where, for example, $1+4\mathbb{Z} = \{1+4k | k \in \mathbb{Z}\}\text{.}$ $4\mathbb{Z}$ can also be written $0+4\mathbb{Z}\text{.}$

Convention $\PageIndex{1}$: Distinguished Representatives

Although we have seen that any representative can describe a coset, it is often convenient to select a distinguished representative from each coset. The advantage to doing this is that there is a unique name for each coset in terms of its distinguished representative. In numeric examples such as the one above, the distinguished representative is usually the smallest nonnegative representative. Remember, this is purely a convenience and there is absolutely nothing wrong in writing $-203+4\mathbb{Z}\text{,}$ $5+4\mathbb{Z}\text{,}$ or $621+4\mathbb{Z}$ in place of $1+4\mathbb{Z}$ because $-203, 5, 621 \in 1+4\mathbb{Z}\text{.}$

Before completing the main thrust of this section, we will make note of a significant implication of Theorem $\PageIndex{2}$. Since a finite group is divided into cosets of a common size by any subgroup, we can conclude:

Theorem $\PageIndex{3}$: Lagrange's Theorem

The order of a subgroup of a finite group must divide the order of the group.

One immediate implication of Lagrange's Theorem is that if $p$ is prime, $\mathbb{Z}_p$ has no proper subgroups.

We will now describe the operation on cosets which will, under certain circumstances, result in a group. For most of this section, we will assume that $G$ is an abelian group. This is one sufficient (but not necessary) condition that guarantees that the set of left cosets will form a group.

Definition $\PageIndex{3}$: Operation on Cosets

Let $C$ and $D$ be left cosets of $H\text{,}$ a subgroup of $G$ with representatives $c$ and $d\text{,}$ respectively. Then

$$\begin{equation*} C\otimes D = (c*H) \otimes (d*H) = (c*d)*H \end{equation*}$$

The operation $\otimes$ is called the operation induced on left cosets by $*\text{.}$

In Theorem $\PageIndex{4}$, later in this section, we will prove that if $G$ is an abelian group, $\otimes$ is indeed an operation. In practice, if the group $G$ is an additive group, the symbol $\otimes$ is replaced by $+\text{,}$ as in the following example.

Example $\PageIndex{3}$: Computing with Cosets of $4\mathbb{Z}$

Consider the cosets described in Example $\PageIndex{2}$. For brevity, we rename $0+4\mathbb{Z}\text{,}$ $1+4\mathbb{Z}\text{,}$ $2+4\mathbb{Z}\text{,}$ and $3+4\mathbb{Z}$ with the symbols $\bar{0}\text{,}$ $\bar{1}\text{,}$ $\bar{2}\text{,}$ and $\bar{3}\text{.}$ Let's do a typical calculation, $\bar{1}+\bar{3}\text{.}$ We will see that the result is always going to be $\bar{0}$ , no matter what representatives we select. For example, $9 \in \bar{1}\text{,}$ $7\in \bar{3}\text{,}$ and $9+7=16 \in \bar{0}\text{.}$ Our choice of the representatives $\bar{1}$ and $\bar{3}$ were completely arbitrary.

In general, $C \otimes D$ can be computed in many ways, and so it is necessary to show that the choice of representatives does not affect the result. When the result we get for $C \otimes D$ is always independent of our choice of representatives, we say that “$\otimes$ is well defined.” Addition of cosets is a well-defined operation on the left cosets of 4$\mathbb{Z}$ and is summarized in the following table. Do you notice anything familiar?

$$\begin{equation*} \begin{array}{c|cccc} \otimes & \bar{0} & \bar{1} & \bar{2} & \bar{3}\\ \hline \bar{0} & \bar{0} & \bar{1} & \bar{2} & \bar{3}\\ \bar{1} & \bar{1} & \bar{2} & \bar{3} & \bar{0}\\ \bar{2} & \bar{2} &\bar{3} & \bar{0} & \bar{1}\\ \bar{3} & \bar{3}& \bar{0} & \bar{1} & \bar{2} \\ \end{array} \end{equation*}$$

Example $\PageIndex{4}$: Cosets of the Integers in the Group of Real Numbers

Consider the group of real numbers, $[\mathbb{R}; +]\text{,}$ and its subgroup of integers, $\mathbb{Z}\text{.}$ Every element of $\mathbb{R}/\mathbb{Z}$ has the same cardinality as $\mathbb{Z}\text{.}$ Let $s, t\in \mathbb{R}\text{.}$ $s\in t+\mathbb{Z}$ if $s$ can be written $t+n$ for some $n \in \mathbb{Z}\text{.}$ Hence $s$ and $t$ belong to the same coset if they differ by an integer. (See Exercise $\PageIndex{6}$ for a generalization of this fact.)

Now consider the coset $0.25+\mathbb{Z}\text{.}$ Real numbers that differ by an integer from 0.25 are $1.25, 2.25, 3.25, \ldots$ and $-0.75, -1.75, -2.75, \ldots\text{.}$ If any real number is selected, there exists a representative of its coset that is greater than or equal to 0 and less than 1. We will call that representative the distinguished representative of the coset. For example, 43.125 belongs to the coset represented by 0.125; $-6.382+\mathbb{Z}$ has 0.618 as its distinguished representative. The operation on $\mathbb{R}/\mathbb{Z}$ is commonly called addition modulo 1. A few typical calculations in $\mathbb{R}/\mathbb{Z}$ are

$$\begin{equation*} \begin{array}{c} (0.1+\mathbb{Z})+(0.48+\mathbb{Z}) = 0.58+\mathbb{Z}\\ (0.7+\mathbb{Z})+(0.31+\mathbb{Z}) = 0.01+\mathbb{Z}\\ -(0.41+\mathbb{Z}) = -0.41+\mathbb{Z} = 0.59+\mathbb{Z}\\ \textrm{and in general, } -(a+\mathbb{Z}) = (1 - a)+\mathbb{Z} \end{array}\text{.} \end{equation*}$$

Example $\PageIndex{5}$: Cosets in a Direct Product

Consider $F = (\mathbb{Z}_4\times \mathbb{Z}_2 )/H\text{,}$ where $H=\{(0,0),(0,1)\}\text{.}$ Since $\mathbb{Z}_4 \times \mathbb{Z}_2$ is of order 8, each element of $F$ is a coset containing two ordered pairs. We will leave it to the reader to verify that the four distinct cosets are $(0, 0)+H\text{,}$ $(1,0) +H\text{,}$ $(2, 0)+H$ and $(3, 0)+H\text{.}$ The reader can also verify that $F$ is isomorphic to $\mathbb{Z}_4$ , since $F$ is cyclic. An educated guess should give you a generator.

Example $\PageIndex{6}$

Consider the group $\mathbb{Z}_2{}^4 = \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2$ . Let $H$ be $\langle (1,0,1, 0)\rangle\text{,}$ the cyclic subgroup of $\mathbb{Z}_2{}^4$ generate by (1,0,1,0). Since

$$\begin{equation*} (1,0,1, 0)+(1,0,1, 0)=(1+_21,0+_20,1+_21,0+_20) = (0,0,0,0) \end{equation*}$$

the order of $H$ is 2 and , $\mathbb{Z}_2{}^4/H$ has $\lvert \mathbb{Z}_2^4 /H\rvert =\frac{\lvert \mathbb{Z}_2^4\rvert }{\lvert H\rvert }=\frac{16}{2}= 8$ elements. A typical coset is

$$\begin{equation*} C = (0, 1, 1, 1)+H = \{(0, 1, 1, 1), (1, 1, 0, 1)\} \end{equation*}$$

Note that since $2(0, 1, 1, 1) = (0, 0, 0, 0)\text{,}$ $2C = C\otimes C = H\text{,}$ the identity for the operation on $\mathbb{Z}_2{}^4/H\text{.}$ The orders of non-identity elements of this factor group are all 2, and it can be shown that the factor group is isomorphic to $\mathbb{Z}_2{}^3\text{.}$

Theorem $\PageIndex{4}$: Coset Operation is Well-Defined (Abelian Case)

If $G$ is an abelian group, and $H \leq G\text{,}$ the operation induced on cosets of $H$ by the operation of $G$ is well defined.

Proof

Suppose that $a\text{,}$ $b\text{,}$ and $a'\text{,}$ $b'\text{.}$ are two choices for representatives of cosets $C$ and $D\text{.}$ That is to say that $a, a' \in C\text{,}$ $b, b' \in D\text{.}$ We will show that $a*b$ and $a'*b'$ are representatives of the same coset. Theorem $\PageIndex{1}$ implies that $C = a*H$ and $D = b*H\text{,}$ thus we have $a' \in a*H$ and $b' \in b*H\text{.}$ Then there exists $h_1, h_2 \in H$ such that $a' = a*h_1$ and $b' = b*h_2$ and so

$$\begin{equation*} a'*b' = (a*h_1)*(b*h_2) = (a*b)*(h_1*h_2) \end{equation*}$$

by various group properties and the assumption that $G$ is abelian, which lets us reverse the order in which $b$ and $h_1$ appear in the chain of equalities. This last expression for $a'*b'$ implies that $a'*b' \in (a*b)*H$ since $h_1*h_2 \in H$ because $H$ is a subgroup of $G\text{.}$ Thus, we get the same coset for both pairs of representatives.

Theorem $\PageIndex{5}$

Let $G$ be a group and $H \leq G\text{.}$ If the operation induced on left cosets of $H$ by the operation of $G$ is well defined, then the set of left cosets forms a group under that operation.

Proof

Let $C_1$$,C_2\text{,}$ and $C_3$ be the left cosets with representatives $r_1\text{,}$ $r_2\text{,}$ and $r_3\text{,}$ respectively. The values of $C_1 \otimes \left(C_2 \otimes C_3\right)$ and $\left(C_1\ \otimes C_2\right)\otimes C_3$ are determined by $r_1 * \left(r_2 * r_3\right)$ and $\left(r_1 * r_2\right) * r_3\text{,}$ respectively. By the associativity of $*$ in $G\text{,}$ these two group elements are equal and so the two coset expressions must be equal. Therefore, the induced operation is associative. As for the identity and inverse properties, there is no surprise. The identity coset is $H\text{,}$ or $e*H\text{,}$ the coset that contains $G$'s identity. If $C$ is a coset with representative $a\text{;}$ that is, if $C = a*H\text{,}$ then $C^{-1}$ is $a^{-1}*H\text{.}$

$$\begin{equation*} (a*H)\otimes \left(a^{-1}*H\right) = \left(a*a^{-1}\right)*H = e*H = \textrm{ identity} \textrm{ coset}\text{.} \end{equation*}$$

Definition $\PageIndex{4}$: Factor Group

Let $G$ be a group and $H \leq G\text{.}$ If the set of left cosets of $H$ forms a group, then that group is called the factor group of “$G$ modulo $H\text{.}$” It is denoted $G/H\text{.}$

Note $\PageIndex{2}$

If $G$ is abelian, then every subgroup of $G$ yields a factor group. We will delay further consideration of the non-abelian case to Section 15.4.

Remark $\PageIndex{2}$: On Notation

It is customary to use the same symbol for the operation of $G/H$ as for the operation on $G\text{.}$ The reason we used distinct symbols in this section was to make the distinction clear between the two operations.

Exercises

Exercise $\PageIndex{1}$

Consider $\mathbb{Z}_{10}$ and the subsets of $\mathbb{Z}_{10}\text{,}$ $\{0, 1, 2, 3, 4\}$ and $\{5, 6, 7, 8, 9\}\text{.}$ Why is the operation induced on these subsets by modulo 10 addition not well defined?

Answer

An example of a valid correct answer: Call the subsets $A$ and $B$ respectively. If we choose $0 \in A$ and $5 \in B$ we get $0 +_{10} 5 =5 \in B\text{.}$ On the other hand, if we choose $3 \in A$ and $8 \in B\text{,}$ we get $3 +_{10} 8 = 1 \in A\text{.}$ Therefore, the induced operation is not well defined on $\{A,B\}\text{.}$

Exercise $\PageIndex{2}$

Can you think of a group $G\text{,}$ with a subgroup $H$ such that $\lvert H\rvert = 6$ and $\lvert G/H\rvert = 6\text{?}$ Is your answer unique?

Exercise $\PageIndex{3}$

For each group and subgroup, what is $G/H$ isomorphic to?

1. $G = \mathbb{Z}_4 \times \mathbb{Z}_2$ and $H = \langle (2, 0)\rangle\text{.}$ Compare to Example $\PageIndex{5}$.
2. $G = [\mathbb{C}; +]$ and $H = \mathbb{R}\text{.}$
3. $G$ = $\mathbb{Z}_{20}$ and $H = \langle 8\rangle\text{.}$

Answer

1. The four distinct cosets in $G/H$ are $H = \{(0, 0), (2, 0)\}\text{,}$ $(1, 0) + H= \{(1,0),(3,0)\}\text{,}$ $(0, 1) + H= \{(0,1),(2,1)\}\text{,}$ and $(1, 1) + H= \{(1,1),(3,1)\}\text{.}$ None of these cosets generates $G/H\text{;}$ therefore $G/H$ is not cyclic. Hence $G/H$ must be isomorphic to $\mathbb{Z}_2\times \mathbb{Z}_2\text{.}$
2. The factor group is isomorphic to $[\mathbb{R}; +]\text{.}$ Each coset of $\mathbb{R}$ is a line in the complex plane that is parallel to the x-axis: $\tau :\mathbb{C}/\mathbb{R}\to \mathbb{R}\text{,}$ where $T(\{a + b i\mid a\in \mathbb{R}\}) = b$ is an isomorphism.
3. $\langle 8\rangle = \{0, 4, 8, 12, 16\}$$\Rightarrow$ $\lvert \mathbb{Z}_{20}/\langle 8\rangle \rvert =4\text{.}$ The four cosets are: $\bar{0}\text{,}$ $\bar{1}\text{,}$ $\bar{2}\text{,}$ and $\bar{3}\text{.}$ 1 generates all four cosets. The factor group is isomorphic to $[\mathbb{Z}_4; +_4]$ because $\bar{1}$ is a generator.

Exercise $\PageIndex{4}$

For each group and subgroup, what is $G/H$ isomorphic to?

1. $G = \mathbb{Z}\times \mathbb{Z}$ and $H = \{(a, a) | a \in \mathbb{Z}\}\text{.}$
2. $G = \left[\mathbb{R}^*; \cdot \right]$ and $H = \{1, -1\}\text{.}$
3. $G =\mathbb{Z}_2{}^5$ and $H = \langle (1, 1, 1, 1, 1)\rangle\text{.}$

Exercise $\PageIndex{5}$

Assume that $G$ is a group, $H \leq G\text{,}$ and $a, b \in G\text{.}$ Prove that $a*H= b*H$ if and only if $b^{-1}*a \in H\text{.}$

Answer

$$\begin{equation*} \begin{split} a*H= b*H &\Leftrightarrow a \in b H\\ &\Leftrightarrow a = b * h \textrm{ for some }h \in H\\ &\Leftrightarrow b^{-1}*a = h \textrm{ for some }h \in H\\ & \Leftrightarrow b^{-1}*a \in H\\ \end{split} \end{equation*}$$

Exercise $\PageIndex{6}$

1. Real addition modulo $r\text{,}$ $r > 0\text{,}$ can be described as the operation induced on cosets of $\langle r\rangle$ by ordinary addition. Describe a system of distinguished representatives for the elements of $\mathbb{R}/\langle r\rangle\text{.}$
2. Consider the trigonometric function sine. Given that $\sin (x+2\pi k) = \sin x$ for all $x\in \mathbb{R}$ and $k\in \mathbb{Z}\text{,}$ show how the distinguished representatives of $\mathbb{R}/\langle 2\pi \rangle$ can be useful in developing an algorithm for calculating the sine of a number.

Exercise $\PageIndex{7}$

Complete the proof of Theorem $\PageIndex{2}$ by proving that if $a \in G\text{,}$ $\rho:H \to a*H$ defined by $\rho(h)= a*h$ is a bijection.