6.4: Onto Functions

One-to-one functions focus on the elements in the domain. We do not want any two of them sharing a common image. Onto functions focus on the codomain. We want to know if it contains elements not associated with any element in the domain.

Definition: surjection

A function \(f :{A}\to{B}\) is onto if, for every element \(b\in B\), there exists an element \(a\in A\) such that \[f(a) = b. \nonumber\] An onto function is also called a surjection, and we say it is surjective.

Example \(\PageIndex{1}\label{eg:ontofcn-01}\)

The graph of the piecewise-defined functions \(h :{[1,3]}\to{[2,5]}\) defined by

\[h(x) = \cases{ 3x- 1 & if $1\leq x\leq 2$, \cr -3x+11 & if $2 < x\leq 3$, \cr} \nonumber\]

is displayed on the left in Figure \(\PageIndex{1}\). It is clearly onto, because, given any \(y\in[2,5]\), we can find at least one \(x\in[1,3]\) such that \(h(x)=y\). Likewise, the function \(k :{[1,3]}\to{[2,5]}\) defined by

\[k(x) = \cases{ 3x- 1 & if $1\leq x\leq 2$, \cr 5 & if $2 < x\leq 3$, \cr}\nonumber\]

is also onto. Its graph is displayed on the right of Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\): Two onto functions from [1,3] to [2,5].

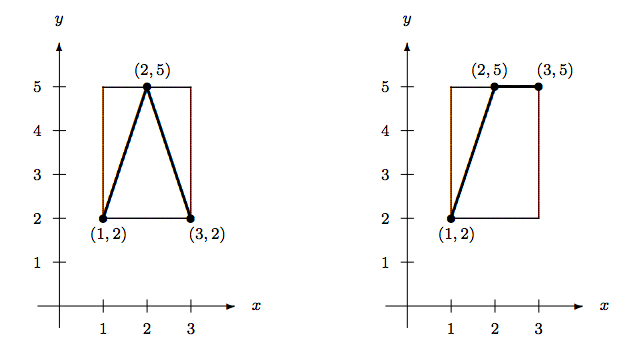
exercise \(\PageIndex{1}\label{he:ontofcn-01}\)

The two functions in Example 6.4.1 are onto but not one-to-one. Construct a one-to-one and onto function \(f\) from \([1,3]\) to \([2,5]\).

exercise \(\PageIndex{2}\label{he:ontofcn-02}\)

Construct a function \(g :{[1,3]}\to{[2,5]}\) that is one-to-one but not onto.

exercise \(\PageIndex{3}\label{he:ontofcn-03}\)

Find a subset \(B\) of \(\mathbb{R}\) that would make the function \(s :{\mathbb{R}}\to{B}\) defined by \(s(x) = x^2\) an onto function.

Example \(\PageIndex{2}\label{eg:ontofcn-02}\)

Construct a function \(g :{(5,8)}\to{\mathbb{R}}\) that is both one-to-one and onto

Remark

This is a challenging problem. Since the domain is an open interval, a straight line graph does not work, because it will not cover every number in the codomain.

Solution

The solution is based on the observation that the function \(h :{(-\frac{\pi}\to{2},\frac{\pi}{2})}{\mathbb{R}}\) defined by \(h(x)=\tan x\) is one-to-one and onto. For this to work in this problem, we need to shift and scale the interval \((5,8)\) to the same size as \((-\frac{\pi}{2},\frac{\pi}{2})\).

First, we have to shift the center of the interval \((5,8)\) to the center of the interval \((-\frac{\pi}{2},\frac{\pi}{2})\). The midpoint of the interval \((5,8)\) is \(\frac{5+8}{2}=\frac{13}{2}\), and the midpoint of \((-\frac{\pi}{2},\frac{\pi}{2})\) is 0. Hence, we need to shift the interval \((5,8)\) to the left \(\frac{13}{2}\) units. This means we need to use the transformation \(x-\frac{13}{2}\). The two endpoints 5 and 8 become \(-\frac{3}{2}\) and \(\frac{3}{2}\), respectively:

\[\begin{array}{|c||c|c|c|} \hline x & 5 & \frac{13}{2} & 8 \\ \hline x-\frac{13}{2} &-\frac{3}{2} & 0 & \frac{3}{2} \\ \hline \end{array} \nonumber\]

After the transformation \(x-\frac{13}{2}\), the original interval \((5,8)\) becomes the interval \((-\frac{3}{2},\frac{3}{2})\). Next, we want to stretch the interval \((-\frac{3}{2},\frac{3}{2})\) into \((-\frac{\pi}{2},\frac{\pi}{2})\). This calls for a scaling factor of \(\frac{\pi}{3}\).

\[\begin{array}{|c||c|c|c|} \hline x & 5 & \frac{13}{2}& 8 \\ \hline \frac{\pi}{3}\left(x-\frac{13}{2}\right) &-\frac{\pi}{2}& 0 &\frac{\pi}{2}\\ \hline \end{array} \nonumber\]

Putting these transformations together, we conclude that \[g(x) = \tan\left[\frac{\pi}{3}\left(x-\frac{13}{2}\right)\right] \nonumber\] gives a one-to-one and onto function from \((5,8)\) to \(\mathbb{R}\).

exercise \(\PageIndex{4}\label{he:ontofcn-04}\)

Construct a function \(h :{(2,9)}\to{\mathbb{R}}\) that is both one-to-one and onto.

In general, how can we tell if a function \(f :{A}\to{B}\) is onto? The key question is: given an element \(y\) in the codomain, is it the image of some element \(x\) in the domain? If it is, we must be able to find an element \(x\) in the domain such that \(f(x)=y\). Mathematically, if the rule of assignment is in the form of a computation, then we need to solve the equation \(y=f(x)\) for \(x\). If we can always express \(x\) in terms of \(y\), and if the resulting \(x\)-value is in the domain, the function is onto.

Example \(\PageIndex{3}\label{eg:ontofcn-03}\)

Is the function \(p :{\mathbb{R}}\to{\mathbb{R}}\) defined by \(p(x)=3x^2-4x+5\) onto?

Solution 1

Let \(y=3x^2-4x+5\), we want to know if we can always express \(x\) in terms of \(y\). Rearranging the equation, we find \[3x^2-4x+(5-y) = 0. \nonumber\] We want this equation to be solvable over \(\mathbb{R}\), that is, we want its solutions to be real. This requires its discriminant to be nonnegative. So we need

\[(-4)^2-4\cdot3\cdot(5-y) = 12y-44 \geq 0. \nonumber\]

We have real solutions only when \(y\geq\frac{11}{3}\). This means, when \(y<\frac{11}{3}\), we cannot find an \(x\)-value such that \(p(x)=y\). Therefore, \(p\) is not onto.

Solution 2

By completing the square, we find

\[p(x) = 3x^2-4x+5 = 3\left(x-\frac{2}{3}\right)^2 + \frac{11}{3} \geq \frac{11}{3}. \nonumber\]

Since \(p(x)\not<\frac{11}{3}\), it is clear that \(p\) is not onto.

exercise \(\PageIndex{5}\label{he:ontofcn-05}\)

The function \(g :{\mathbb{R}}\to{\mathbb{R}}\) is defined as \(g(x)=3x+11\). Prove that it is onto.

Example \(\PageIndex{4}\label{eg:ontofcn-04}\)

Is the function \(p :{\mathbb{R}}\to{\mathbb{R}}\) defined by

\[p(x) = \cases{ 4x+1 & if $x\leq3$ \cr \frac{1}{2} \,x & if $x>3$ \cr} \nonumber\]

\[p(x) = \cases{ 4x+1 & if $x\leq3$ \cr \frac{1}{2} & if $x > 3$ \cr}\nonumber\]

an onto function?

Solution

The graphs \(y=4x+1\) and \(y=\frac{1}{2}\,x\) are both increasing. For \(x\leq3\), the \(y\)-values cover the range \((-\infty,13)\), and for \(x>3\), the \(y\)-values cover the range \(\big(\frac{3}{2},\infty\big)\). Since these two \(y\)-ranges overlap, all the \(y\)-values are being covered by the images. Therefore, \(p\) is onto.

exercise \(\PageIndex{6}\label{he:ontofcn-06}\)

Determine whether \[f(x) = \cases{ 3x+1 & if $x\leq2$ \cr 4x & if $x > 2$ \cr}\nonumber\] is an onto function.

Example \(\PageIndex{5}\label{eg:ontofcn-05}\)

Consider the function \(g :{\mathbb{Z}_{43}}\to{\mathbb{Z}_{43}}\) defined by

\[g(x) \equiv 11x-5 \pmod{43}.\nonumber\]

Let \[y = g(x) \equiv 11x-5 \pmod{43},\nonumber\]

then \[x \equiv 11^{-1}(y+5) \equiv 4(y+5) \pmod{43}.\nonumber\]

This shows that \(g\) is onto.

exercise \(\PageIndex{7}\label{he:ontofcn-07}\)

Show that the function \(h :{\mathbb{Z}_{23}}\to{\mathbb{Z}_{23}}\) defined by \(h(x) \equiv 5x+8\) (mod 23) is onto.

Example \(\PageIndex{6}\label{eg:ontofcn-06}\)

Is the function \({u}:{\mathbb{Z}}\to{\mathbb{Z}}\) defined by

\[u(n) = \cases{ 2n & if $n\geq0$ \cr -n & if $n < 0$ \cr} \nonumber\]

one-to-one? Is it onto?

Solution

Since \(u(-2)=u(1)=2\), the function \(u\) is not one-to-one. Since \(u(n)\geq0\) for any \(n\in\mathbb{Z}\), the function \(u\) is not onto.

exercise \(\PageIndex{8}\label{he:ontofcn-08}\)

Is the function \(v:{\mathbb{N}}\to{\mathbb{N}}\) defined by \(v(n)=n+1\) onto? Explain.

Example \(\PageIndex{7}\label{eg:oneonefcn-07}\)

The function \(s\) in Example 6.4.10 is both one-to-one and onto. It provides a one-to-one correspondence between the elements of \(A\) by matching a married individual to his/her spouse.

exercise \(\PageIndex{9}\label{he:ontofcn-09}\)

Is the function \(h_1\) in Exercises 1.2, Problem 6.4.8, an onto function? Explain.

Summary and Review

• A function \(f :{A}\to{B}\) is onto if, for every element \(b\in B\), there exists an element \(a\in A\) such that \(f(a)=b\).
• To show that \(f\) is an onto function, set \(y=f(x)\), and solve for \(x\), or show that we can always express \(x\) in terms of \(y\) for any \(y\in B\).
• To show that a function is not onto, all we need is to find an element \(y\in B\), and show that no \(x\)-value from \(A\) would satisfy \(f(x)=y\).

exercise \(\PageIndex{1}\label{ex:ontofcn-01}\)

Which of the following functions are onto? Explain!

1. \(f :{\mathbb{R}}\to{\mathbb{R}}\), \(f(x)=x^3-2x^2+1\).
2. \(g :{[\,2,\infty)}\to{\mathbb{R}}\), \(g(x)=x^3-2x^2+1\).

exercise \(\PageIndex{2}\label{ex:ontofcn-02}\)

Which of the following functions are onto? Explain!

1. \(p :{\mathbb{R}}\to{\mathbb{R}}\), \(p(x)=e^{1-2x}\).
2. \(q :{\mathbb{R}}\to{\mathbb{R}}\), \(q(x)=|1-3x|\).

exercise \(\PageIndex{3}\label{ex:ontofcn-03}\)

Construct a one-to-one function \(f :{[1,3]}\to{[2,5]}\) that is not onto.

exercise \(\PageIndex{4}\label{ex:ontofcn-04}\)

Construct an onto function \(g :{[\,2,5)}\to{(1,4\,]}\) that is not one-to-one.

exercise \(\PageIndex{5}\label{ex:ontofcn-05}\)

Determine which of the following are onto functions.

1. \(f :{\mathbb{Z}}\to{\mathbb{Z}}\); \(f(n)=n^3+1\)
2. \(g :{\mathbb{Q}}\to{\mathbb{Q}}\); \(g(x)=n^2\)
3. \(h :{\mathbb{R}}\to{\mathbb{R}}\); \(h(x)=x^3-x\)
4. \(k :{\mathbb{R}}\to{\mathbb{R}}\); \(k(x)=5^x\)

exercise \(\PageIndex{6}\label{ex:ontofcn-06}\)

Determine which of the following are onto functions.

1. \(p :{\wp(\{1,2,3,\ldots,n\})}\to{\{0,1,2,\ldots,n\}}\); \(p(S)=|S|\)
2. \(q :{\wp(\{1,2,3,\ldots,n\})}\to{\wp(\{1,2,3,\ldots,n\})}\); \(q(S)=\overline{S}\)

exercise \(\PageIndex{7}\label{ex:ontofcn-07}\)

Determine which of the following functions are onto.

1. \({f_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d\}}\); \(f_1(1)=b\), \(f_1(2)=c\), \(f_1(3)=a\), \(f_1(4)=a\), \(f_1(5)=c\)
2. \({f_2}:{\{1,2,3,4\}}\to{\{a,b,c,d,e\}}\); \(f_2(1)=c\), \(f_2(2)=b\), \(f_2(3)=a\), \(f_2(4)=d\)
3. \({f_3}:{\mathbb{Z}}\to{\mathbb{Z}}\); \(f_5(n)=-n\)
4. \({f_4}:{\mathbb{Z}}\to{\mathbb{Z}}\); \(f_4(n) = \cases{ 2n & if $n < 0$, \cr -3n & if $n\geq0$,\cr}\)

exercise \(\PageIndex{8}\label{ex:ontofcn-08}\)

Determine which of the following functions are onto.

1. \({g_1}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_1(1)=b\), \(g_1(2)=b\), \(g_1(3)=b\), \(g_1(4)=a\), \(g_1(5)=d\)
2. \({g_2}:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}\); \(g_2(1)=d\), \(g_2(2)=b\), \(g_2(3)=e\), \(g_2(4)=a\), \(g_2(5)=c\)
3. \(g_3: \mathbb{N} \rightarrow \mathbb{N}\); \(g_3 (n) = \cases{ \frac{n+1}{2} & if $n$ is odd \cr \frac{n}{2} & if $n$ is even \cr}\)
4. \(g_4: \mathbb{N} \rightarrow \mathbb{N}\); \(g_4 (n) = \cases{ n+1 & if $n$ is odd \cr n-1 & if $n$ is even \cr}\)

exercise \(\PageIndex{9}\label{ex:ontofcn-09}\)

Is it possible for a function from \(\{1,2\}\) to \(\{a,b,c,d\}\) to be onto? Explain.

exercise \(\PageIndex{10}\label{ex:ontofcn-10}\)

List all the onto functions from \(\{1,2,3,4\}\) to \(\{a,b\}\)?

Hint

List the images of each function.

exercise \(\PageIndex{11}\label{ex:ontofcn-11}\)

Determine which of the following functions are onto.

1. \(f :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(h(n)\equiv 3n\) (mod 10).
2. \(g :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(g(n)\equiv 5n\) (mod 10).
3. \(h :{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(h(n)\equiv 3n\) (mod 36).

exercise \(\PageIndex{12}\label{ex:ontofcn-12}\)

Determine which of the following functions are onto.

1. \(r:{\mathbb{Z}_{36}}\to{\mathbb{Z}_{36}}\); \(r(n)\equiv 5n\) (mod 36).
2. \(s :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(s(n)\equiv n+5\) (mod 10).
3. \(t :{\mathbb{Z}_{10}}\to{\mathbb{Z}_{10}}\); \(t(n)\equiv 3n+5\) (mod 10).

exercise \(\PageIndex{13}\label{ex:ontofcn-13}\)

Determine which of the following functions are onto.

1. \({\alpha}:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{ 7}}\); \(\alpha(n)\equiv 2n\) (mod 7).
2. \({\beta} :{\mathbb{Z}_{ 8}}\to{\mathbb{Z}_{12}}\); \(\beta (n)\equiv 3n\) (mod 12).
3. \({\gamma}:{\mathbb{Z}_{ 6}}\to{\mathbb{Z}_{12}}\); \(\gamma(n)\equiv 2n\) (mod 12).
4. \({\delta}:{\mathbb{Z}_{12}}\to{\mathbb{Z}_{36}}\); \(\delta(n)\equiv 6n\) (mod 36).

exercise \(\PageIndex{14}\label{ex:ontofcn-14}\)

Give an example of a function \(f :{\mathbb{N}}{\mathbb{N}}\) that is

1. neither one-to-one nor onto
2. one-to-one but not onto
3. onto but not one-to-one
4. both one-to-one and onto