5.7: Connectivity

We have seen examples of connected graphs and graphs that are not connected. While "not connected'' is pretty much a dead end, there is much to be said about "how connected'' a connected graph is. The simplest approach is to look at how hard it is to disconnect a graph by removing vertices or edges. We assume that all graphs are simple.

If it is possible to disconnect a graph by removing a single vertex, called a cutpoint, we say the graph has connectivity 1. If this is not possible, but it is possible to disconnect the graph by removing two vertices, the graph has connectivity 2.

Definition $\PageIndex{1}$: Cutset

If a graph $G$ is connected, any set of vertices whose removal disconnects the graph is called a cutset. $G$ has connectivity $k$ if there is a cutset of size $k$ but no smaller cutset. If there is no cutset and $G$ has at least two vertices, we say $G$ has connectivity $n-1$; if $G$ has one vertex, its connectivity is undefined. If $G$ is not connected, we say it has connectivity $0$. $G$ is $k$-connected if the connectivity of $G$ is at least $k$. The connectivity of $G$ is denoted $\kappa(G)$.

As you should expect from the definition, there are graphs without a cutset: the complete graphs $K_n$. If $G$ is connected but not a $K_n$, it has vertices $v$ and $w$ that are not adjacent, so removing the $n-2$ other vertices leaves a non-connected graph, and so the connectivity of $G$ is at most $n-2$. Thus, only the complete graphs have connectivity $n-1$.

We do the same thing for edges:

Definition $\PageIndex{2}$: Cut

If a graph $G$ is connected, any set of edges whose removal disconnects the graph is called a cut. $G$ has edge connectivity $k$ if there is a cut of size $k$ but no smaller cut; the edge connectivity of a one-vertex graph is undefined. $G$ is $k$-edge-connected if the edge connectivity of $G$ is at least $k$. The edge connectivity is denoted $\lambda(G)$.

Any connected graph with at least two vertices can be disconnected by removing edges: by removing all edges incident with a single vertex the graph is disconnected. Thus, $\lambda(G)\le \delta(G)$, where $\delta(G)$ is the minimum degree of any vertex in $G$. Note that $\delta(G)\le n-1$, so $\lambda(G)\le n-1$.

Removing a vertex also removes all of the edges incident with it, which suggests that $\kappa(G)\le\lambda(G)$. This turns out to be true, though not as easy as you might hope. We write $G-v$ to mean $G$ with vertex $v$ removed, and $G-\{v_1,v_2,\ldots,v_k\}$ to mean $G$ with all of $\{v_1,v_2,\ldots,v_k\}$ removed, and similarly for edges.

Theorem $\PageIndex{1}$

$\kappa(G)\le\lambda(G)$.

Proof

We use induction on $\lambda=\lambda(G)$. If $\lambda=0$, $G$ is disconnected, so $\kappa=0$. If $\lambda=1$, removal of edge $e$ with endpoints $v$ and $w$ disconnects $G$. If $v$ and $w$ are the only vertices of $G$, $G$ is $K_2$ and has connectivity $1$. Otherwise, removal of one of $v$ and $w$ disconnects $G$, so $\kappa=1$.

As a special case we note that if $\lambda=n-1$ then $\delta=n-1$, so $G$ is $K_n$ and $\kappa=n-1$.

Now suppose $n-1>\lambda=k>1$, and removal of edges $e_1,e_2,\ldots,e_k$ disconnects $G$. Remove edge $e_k$ with endpoints $v$ and $w$ to form $G_1$ with $\lambda(G_1)=k-1$. By the induction hypothesis, there are at most $k-1$ vertices $v_1,v_2,\ldots,v_j$ such that $G_2=G_1-\{v_1,v_2,\ldots,v_j\}$ is disconnected. Since $k< n-1$, $k-1\le n-3$, and so $G_2$ has at least $3$ vertices.

If both $v$ and $w$ are vertices of $G_2$, and if adding $e_k$ to $G_2$ produces a connected graph $G_3$, then removal of one of $v$ and $w$ will disconnect $G_3$ forming $G_4$, and $G_4=G-\{v_1,v_2,\ldots,v_j,v\}$ or $G_4=G-\{v_1,v_2,\ldots,v_j,w\}$, that is, removing at most $k$ vertices disconnects $G$. If $v$ and $w$ are vertices of $G_2$ but adding $e_k$ does not produce a connected graph, then removing $v_1,v_2,\ldots,v_j$ disconnects $G$. Finally, if at least one of $v$ and $w$ is not in $G_2$, then $G_2=G-\{v_1,v_2,\ldots,v_j\}$ and the connectivity of $G$ is less than $k$. So in all cases, $\kappa\le k$.

Graphs that are 2-connected are particularly important, and the following simple theorem is useful.

Theorem $\PageIndex{2}$

If $G$ has at least three vertices, the following are equivalent:

1. $G$ is 2-connected
2. $G$ is connected and has no cutpoint
3. For all distinct vertices $u$, $v$, $w$ in $G$ there is a path from $u$ to $v$ that does not contain $w$.

Proof

$\bf 1\Rightarrow3$: Since $G$ is 2-connected, $G$ with $w$ removed is a connected graph $G'$. Thus, in $G'$ there is a path from $u$ to $v$, which in $G$ is a path from $u$ to $v$ avoiding $w$.

$\bf 3\Rightarrow2$: If $G$ has property 3 it is clearly connected. Suppose that $w$ is a cutpoint, so that $G'=G-w$ is disconnected. Let $u$ and $v$ be vertices in two different components of $G'$, so that no path connects them in $G'$. Then every path joining $u$ to $v$ in $G$ must use $w$, a contradiction.

$\bf 2\Rightarrow1$: Since $G$ has at least 3 vertices and has no cutpoint, its connectivity is at least 2, so it is 2-connected by definition.

There are other nice characterizations of 2-connected graphs.

Theorem $\PageIndex{3}$

If $G$ has at least three vertices, then $G$ is 2-connected if and only if every two vertices $u$ and $v$ are contained in a cycle.

Proof

if: Suppose vertex $w$ is removed from $G$, and consider any other vertices $u$ and $v$. In $G$, $u$ and $v$ lie on a cycle; even if $w$ also lies on this cycle, then $u$ and $v$ are still connected by a path when $w$ is removed.

only if: Given $u$ and $v$ we want to show there is a cycle containing both. Let $U$ be the set of vertices other than $u$ that are contained in a cycle with $u$. First, we show that $U$ is non-empty. Let $w$ be adjacent to $u$, and remove the edge $e$ between them. Since $\lambda(G)\ge \kappa(G)\ge 2$, $G-e$ is connected. Thus, there is a path from $u$ to $w$; together with $e$ this path forms a cycle containing $u$ and $w$, so $w\in U$.

For a contradiction, suppose $v\notin U$. Let $w$ be in $U$ with $\text{d}(w,v)\ge 1$ as small as possible, fix a cycle $C$ containing $u$ and $w$ and a path $P$ of length $\text{d}(w,v)$ from $w$ to $v$. By the previous theorem, there is a path $Q$ from $u$ to $v$ that does not use $w$. Following this path from $u$, there is a last vertex $x$ on the path that is also on the cycle containing $u$ and $w$, and there is a first vertex $y$ on the path, after $x$, with $y$ also on the path from $w$ to $v$ (it is possible that $y=v$, but not that $y=w$); see Figure $\PageIndex{1}$. Now starting at $u$, proceeding on cycle $C$ to $x$ without using $w$, then from $x$ to $y$ on $Q$, then to $w$ on $P$, and finally back to $u$ on $C$, we see that $y\in U$. But $y$ is closer to $v$ than is $w$, a contradiction. Hence $v\in U$.

Figure $\PageIndex{1}$: Point $y$ closer to $v$ than $w$ is a contradition; path $Q$ is shown dashed. (See Theorem $\PageIndex{3}$.)

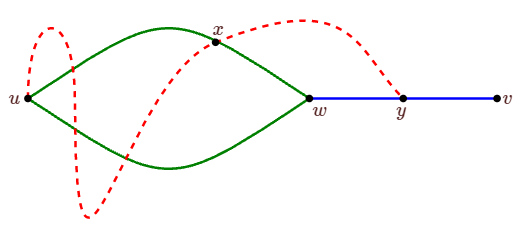
The following corollary is an easy restatement of this theorem.

Corollary $\PageIndex{1}$

If $G$ has at least three vertices, then $G$ is 2-connected if and only if between every two vertices $u$ and $v$ there are two internally disjoint paths between $v$ and $w$, that is, paths that share only the vertices $v$ and $w$.

This version of the theorem suggests a generalization:

Theorem $\PageIndex{4}$: Menger's Theorem

If $G$ has at least $k+1$ vertices, then $G$ is $k$-connected if and only if between every two vertices $u$ and $v$ there are $k$ pairwise internally disjoint paths.

Proof

Suppose first that between every two vertices $v$ and $w$ in $G$ there are $k$ internally disjoint paths. If $G$ is not $k$-connected, the connectivity of $G$ is at most $k-1$, and because $G$ has at least $k+1$ vertices, there is a cutset $S$ of $G$ with size at most $k-1$. Let $v$ and $w$ be vertices in two different components of $G-S$; in $G$ these vertices are joined by $k$ internally disjoint paths. Since there is no path from $v$ to $w$ in $G-S$, each of these $k$ paths contains a vertex of $S$, but this is impossible since $S$ has size less than $k$, and the paths share no vertices other than $v$ and $w$. This contradiction shows that $G$ is $k$-connected.

Now suppose $G$ is $k$-connected.

If $v$ and $w$ are not adjacent, $\kappa_G(v,w)\ge k$ and by the previous theorem there are $p_G(v,w)=\kappa_G(v,w)$ internally disjoint paths between $v$ and $w$.

If $v$ and $w$ are connected by edge $e$, consider $G-e$. If there is a cutset of $G-e$ of size less than $k-1$, call it $S$, then either $S\cup\{v\}$ or $S\cup\{w\}$ is a cutset of $G$ of size less than $k$, a contradiction. (Since $G$ has at least $k+1$ vertices, $G-S$ has at least three vertices.) Thus, $\kappa_{G-e}(v,w)\ge k-1$ and by the previous theorem there are at least $k-1$ internally disjoint paths between $v$ and $w$ in $G-e$. Together with the path $v$, $w$ using edge $e$, these form $k$ internally disjoint paths between $v$ and $w$ in $G$.

We first prove Menger's original version of this, a "local'' version.

Definition $\PageIndex{3}$: Separating Set

If $v$ and $w$ are non-adjacent vertices in $G$, $\kappa_G(v,w)$ is the smallest number of vertices whose removal separates $v$ from $w$, that is, disconnects $G$ leaving $v$ and $w$ in different components. A cutset that separates $v$ and $w$ is called a separating set for $v$ and $w$. $p_G(v,w)$ is the maximum number of internally disjoint paths between $v$ and $w$.

Theorem $\PageIndex{5}$

If $v$ and $w$ are non-adjacent vertices in $G$, $\kappa_G(v,w)=p_G(v,w)$.

Proof

If there are $k$ internally disjoint paths between $v$ and $w$, then any set of vertices whose removal separates $v$ from $w$ must contain at least one vertex from each of the $k$ paths, so $\kappa_G(v,w)\ge p_G(v,w)$.

To finish the proof, we show that there are $\kappa_G(v,w)$ internally disjoint paths between $v$ and $w$. The proof is by induction on the number of vertices in $G$. If $G$ has two vertices, $G$ is not connected, and $\kappa_G(v,w)=p_G(v,w)=0$. Now suppose $G$ has $n>2$ vertices and $\kappa_G(v,w)=k$.

Note that removal of either $N(v)$ or $N(w)$ separates $v$ from $w$, so no separating set $S$ of size $k$ can properly contain $N(v)$ or $N(w)$. Now we address two cases:

Case 1: Suppose there is a set $S$ of size $k$ that separates $v$ from $w$, and $S$ contains a vertex not in $N(v)$ or $N(w)$. $G-S$ is disconnected, and one component $G_1$ contains $v$. Since $S$ does not contain $N(v)$, $G_1$ has at least two vertices; let $X=V(G_1)$ and $Y=V(G)-S-X$. Since $S$ does not contain $N(w)$, $Y$ contains at least two vertices. Now we form two new graphs: Form $H_X$ by starting with $G-Y$ and adding a vertex $y$ adjacent to every vertex of $S$. Form $H_Y$ by starting with $G-X$ and adding a vertex $x$ adjacent to every vertex of $S$; see Figure $\PageIndex{2}$. Since $X$ and $Y$ each contain at least two vertices, $H_X$ and $H_Y$ are smaller than $G$, and so the induction hypothesis applies to them.

Clearly $S$ separates $v$ from $y$ in $H_X$ and $w$ from $x$ in $H_Y$. Moreover, any set that separates $v$ from $y$ in $H_X$ separates $v$ from $w$ in $G$, so $\kappa_{H_X}(v,y)=\kappa_G(v,w)=k$. Similarly, $\kappa_{H_Y}(x,w)=\kappa_G(v,w)=k$. Hence, by the induction hypothesis, there are $k$ internally disjoint paths from $v$ to $y$ in $H_X$ and $k$ internally disjoint paths from $x$ to $w$ in $H_Y$. Each of these paths uses one vertex of $S$; by eliminating $x$ and $y$ and joining the paths at the vertices of $S$, we produce $k$ internally disjoint paths from $v$ to $w$.

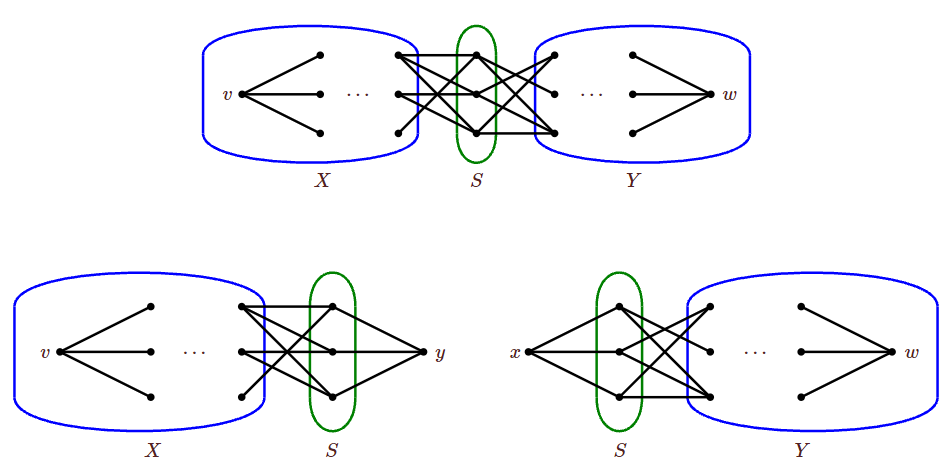
Figure $\PageIndex{2}$: Case 1: Top figure is $G$, lower left is $H_X$, lower right is $H_Y$.

Case 2: Now we suppose that any set $S$ separating $v$ and $w$ is a subset of $N(v)\cup N(w)$; pick such an $S$. If there is a vertex $u$ not in $\{v,w\}\cup N(v)\cup N(w)$, consider $G-u$. This $u$ is not in any set of size $k$ that separates $v$ from $w$, for if it were we would be in Case 1. Since $S$ separates $v$ from $w$ in $G-u$, $\kappa_{G-u}(v,w)\le k$. But if some smaller set $S'$ separates $v$ from $w$ in $G-u$, then $S'\cup\{u\}$ separates $v$ from $w$ in $G$, a contradiction, so $\kappa_{G-u}(v,w)=k$. By the induction hypothesis, there are $k$ internally disjoint paths from $v$ to $w$ in $G-u$ and hence in $G$.

We are left with $V(G)=\{v,w\}\cup N(v)\cup N(w)$. Suppose there is a vertex $u$ in $N(v)\cap N(w)$. Then $u$ is in every set that separates $v$ from $w$, so $\kappa_{G-u}=k-1$. By the induction hypothesis, there are $k-1$ internally disjoint paths from $v$ to $w$ in $G-u$ and together with the path $v,u,w$, they comprise $k$ internally disjoint paths from $v$ to $w$ in $G$. Finally, suppose that $N(v)\cap N(w)=\emptyset$. Form a bipartite graph $B$ with vertices $N(v)\cup N(w)$ and any edges of $G$ that have one endpoint in $N(v)$ and the other in $N(w)$. Every set separating $v$ from $w$ in $G$ must include one endpoint of every edge in $B$, that is, must be a vertex cover in $B$, and conversely, every vertex cover in $B$ separates $v$ from $w$ in $G$. Thus, the minimum size of a vertex cover in $B$ is $k$, and so there is a matching in $B$ of size $k$, by Theorem 4.6.4. The edges of this matching, together with the edges incident at $v$ and $w$, form $k$ internally disjoint paths from $v$ to $w$ in $G$.

$$\bullet\quad\bullet\quad\bullet\nonumber$$

We return briefly to 2-connectivity. The next theorem can sometimes be used to provide the induction step in an induction proof.

Theorem $\PageIndex{6}$: The Handle Theorem

Suppose $G$ is 2-connected and $K$ is a 2-connected proper subgraph of $G$. Then there are subgraphs $L$ and $H$ (the handle) of $G$ such that $L$ is 2-connected, $L$ contains $K$, $H$ is a simple path, $L$ and $H$ share exactly the endpoints of $H$, and $G$ is the union of $L$ and $H$.

Proof

Given $G$ and $K$, let $L$ be a maximal proper subgraph of $G$ containing $K$. If $V(L)=V(G)$, let $e$ be an edge not in $L$. Since $L$ plus the edge $e$ is 2-connected, it must be $G$, by the maximality of $L$. Hence $H$ is the path consisting of $e$ and its endpoints.

Suppose that $v$ is in $V(G)$ but not $V(L)$. Let $u$ be a vertex of $L$. Since $G$ is 2-connected, there is a cycle containing $v$ and $u$. Following the cycle from $v$ to $u$, Let $w$ be the first vertex in $L$. Continuing on the cycle from $u$ to $v$, let $x$ be the last vertex in $L$. Let $P$ be the path continuing around the cycle: $(x,v_1,v_2,\ldots,v_k,v=v_{k+1},v_{k+2},\ldots,v_m,w)$. If $x\not=w$, let $H=P$. Since $L$ together with $H$ is 2-connected, it is $G$, as desired.

If $x=w$ then $x=w=u$. Let $y$ be a vertex of $L$ other than $u$. Since $G$ is 2-connected, there is a path $P_1$ from $v$ to $y$ that does not include $u$. Let $v_j$ be the last vertex on $P_1$ that is in $\{v_1,\ldots,v,\ldots,v_m\}$; without loss of generality, suppose $j\ge k+1$. Then let $H$ be the path $(u,v_1,\ldots,v=v_{k+1},\ldots, v_j,\ldots,y)$, where from $v_j$ to $y$ we follow path $P_1$. Now $L\cup H$ is a 2-connected subgraph of $G$, but it is not $G$, as it does not contain the edge $\{u,v_m\}$, contradicting the maximality of $L$. Thus $x\not=w$.

A graph that is not connected consists of connected components. In a theorem reminiscent of this, we see that connected graphs that are not 2-connected are constructed from 2-connected subgraphs and bridges.

Definition $\PageIndex{4}$: Block

A block in a graph $G$ is a maximal induced subgraph on at least two vertices without a cutpoint.

As usual, maximal here means that the induced subgraph $B$ cannot be made larger by adding vertices edges. A block is either a 2-connected induced subgraph or a single edge together with its endpoints. Blocks are useful in large part because of this theorem:

Theorem $\PageIndex{7}$

The blocks of $G$ partition the edges.

Proof

We need to show that every edge is in exactly one block. If an edge is in no 2-connected induced subgraph of $G$, then, together with its endpoints, it is itself a block. Thus, every edge is in some block.

Now suppose that $B_1$ and $B_2$ are distinct blocks. This implies that neither is a subgraph of the other, by the maximality condition. Hence, the induced subgraph $G[V(B_1)\cup V(B_2)]$ is larger than either of $B_1$ and $B_2$. Suppose $B_1$ and $B_2$ share an edge, so that they share the endpoints of this edge, say $u$ and $v$. Supppose $w$ is a vertex in $V(B_1)\cup V(B_2)$. Since $B_1-w$ and $B_2-w$ are connected, so is $G[(V(B_1)\cup V(B_2))\backslash\{w\}]$, because either $u$ or $v$ is in $(V(B_1)\cup V(B_2))\backslash\{w\}$. Thus $G[V(B_1)\cup V(B_2)]$ has no cutpoint and so it is 2-connected and strictly contains $B_1$ and $B_2$, contradicting the maximality property of blocks. Thus, every edge is in at most one block.

If $G$ has a single block, it is either $K_2$ or is 2-connected, and any 2-connected graph has a single block.

Theorem $\PageIndex{8}$

If $G$ is connected but not 2-connected, then every vertex that is in two blocks is a cutpoint of $G$.

Proof

Suppose $w$ is in $B_1$ and $B_2$, but $G-w$ is connected. Then there is a path $v_1,v_2,\ldots,v_k$ in $G-w$, with $v_1\in B_1$ and $v_k\in B_2$. But then $G[V(B_1)\cup V(B_2)\cup \{v_1,v_2,\ldots,v_k\}]$ is 2-connected and contains both $B_1$ and $B_2$, a contradiction.