11.2: Basic Definitions, Terminology, and Notation
- Page ID
- 60128
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now that we have an intuitive understanding of what a graph is, it is time to make a formal definition.
Definitions: Graph, Vertex, and Edge
A graph \(G\) consists of two sets:
\(V\), whose elements are referred to as the vertices of \(G\) (the singular of vertices is vertex); and
\(E\), whose elements are unordered pairs from \(V\) (i.e., \(E ⊆ \{\{v_1, v_2\} | v_1, v_2 ∈ V \}\)). The elements of \(E\) are referred to as the edges of \(G\).
For clarity in situations where more than one graph is being studied, we may use \(E(G)\) for \(E\) and \(V(G)\) for \(V\).
According to this definition, Euler’s model of the bridges of Königsberg is not actually a graph, because some of the vertices have more than one edge between them (for example, there are two edges between \(A\) and \(B\)), which makes \(E\) a multiset rather than a set. This leads naturally to another definition.
Definition: Multiple Edge and Multigraph
For some purposes, we may allow \(E\) to be a multiset rather than a set. When we do this, an element that appears more than once in \(E\) is called a multiple edge or multiedge. A graph that includes at least one multiple edge is called a multigraph.
Another situation that we might like to allow for some purposes but not allow for others, is the possibility of a connection that goes from a node back to itself.
Definition: Loop and Simple Graph
An edge of the form \(\{v, v\}\) for some \(v ∈ V\), is called a loop.
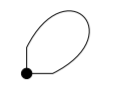
A simple graph is a graph that has no loops or multiple edges.
For most of the graph theory we cover in this course, we will only consider simple graphs. However, there are some results for which the proof is identical whether or not the graph is simple, and other results that actually become easier to prove if we allow multigraphs and/or loops, than if we only allow simple graphs. It is worthwhile and sometimes important to think about which of our results apply to multigraphs (and/or graphs with loops), and which do not. From this point on, unless otherwise specified, you should assume that any time the word “graph” is used, it means a simple graph. However, be aware that many of our definitions and results generalise to multigraphs and to graphs or multigraphs with loops, even where we don’t specify this.
There is still more basic terminology that we need to establish before we can say much about a graph.
Definition: Endvertex
If \(e = \{u, v\}\) is an edge of a graph (or a multigraph, with or without loops), then we say that \(u\) and \(v\) are endvertices (singular: endvertex) of \(e\). We say that \(e\) is incident with \(u\) and \(v\) (or vice versa, the vertices are also incident with the edge), and that \(u\) and \(v\) are adjacent since there is an edge joining them, or that \(u\) is a neighbour of \(v\).
Notation
We use the notation \(u ∼ v\) to denote that \(u\) is adjacent to \(v\). We may also denote the edge \(e = \{u, v\}\) by \(uv\) or by \(vu\).
After one more definition, we will go through some examples using the terminology we have established.
Definition: Valency and Isolated Vertex
If \(v ∈ V\) is a vertex of a graph (simple or multi, with or without loops), then the number of times \(v\) appears as the endvertex of some edge is called the valency of \(v\) in \(G\). (Many sources use degree rather than valency, but the word degree has many meanings in mathematics, making valency a preferable term for this.) A vertex of valency \(0\) is called an isolated vertex.
Note
In a graph without loops, we can define the valency of any vertex \(v\) as the number of edges incident with \(v\). For most purposes, this is a good way to think of the valency. However, when a graph has loops, many formulas work out more nicely if we consider each loop to contribute \(2\) to the valency of its endvertex. This fits the definition we have given, since a vertex \(v\) appears twice as the endvertex of any loop incident with \(v\).
Notation
The valency of \(v\) is denoted by \(\text{val}(v)\) or \(\text{deg}(v)\) or \(d(v)\) or \(d_G(v)\).
Example \(\PageIndex{1}\)
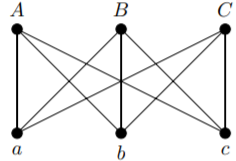
In Figure 11.2.2, the vertices are \(a\), \(b\), \(c\), \(A\), \(B\), and \(C\), and
\(E = \{\{a, A\}, \{a, B\}, \{a, C\}, \{b, A\}, \{b, B\}, \{b, C\}, \{c, A\}, \{c, B\}, \{c, C\}\}\).
Perhaps you can see already why most people prefer to use a diagram rather than a list of vertices and edges to describe a graph!
The vertex a is adjacent to \(A\), \(B\) and \(C\). The vertex \(C\) is not adjacent to \(B\). The edge \(\{a, C\}\) is incident with the vertex \(a\); the vertex \(C\) is also an endvertex of this edge. Every vertex in this graph has valency \(3\), so none of the vertices is isolated. This is a simple graph, as it has no loops or multiple edges.
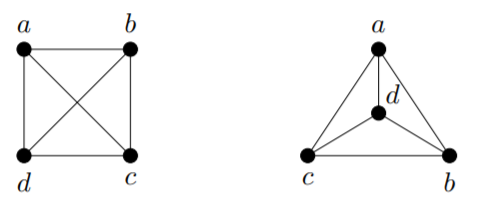
Although a diagram is a convenient and often helpful way to visualise a graph, it is important to note that because a graph is defined by the sets \(V\) and \(E\), it is often possible to draw a particular graph in ways that look quite different. Despite the different-looking drawings, as long as \(V\) and \(E\) are the same, the graph is also the same. In Figure 11.2.3, we see two different drawings of the graph given by \(V = \{a, b, c, d\}\) and \(E = \{\{a, b\}, \{a, c\}, \{a, d\}, \{b, c\}, \{b, d\}, \{c, d\}\}\).
Example \(\PageIndex{2}\)
Let the graph \(G\) be defined by \(V = \{w, x, y, z\}\) and \(E = \{e_1, e_2\}\), where \(e_1 = \{w, x\}\) and \(e_2 = \{w, y\}\). There are no loops or multiple edges, so \(G\) is a simple graph. The edge \(e_2\) has endvertices \(w\) and \(y\). The vertex \(w\) is incident with both \(e_1\) and \(e_2\). The vertices \(x\) and \(y\) are not adjacent. The vertex \(z\) is an isolated vertex, as it has no neighbours. The vertex \(y\) has only one neighbour, \(w\). The valency of \(w\) is \(2\). The valency of \(x\) and the valency of \(y\) are both \(1\). In verifying all of these statements, drawing a diagram of the graph might help you.
Exercise \(\PageIndex{1}\)
For each of the following graphs (which may or may not be simple, and may or may not have loops), find the valency of each vertex. Determine whether or not the graph is simple, and if there is any isolated vertex. List the neighbours of \(a\), and all edges with which \(a is incident.
- Let \(G\) be defined by \(V = \{a, b, c, d, e\}\) and \(E = \{e_1, e_2, e_3, e_4, e_5, e_6\}\) with \(e_1 = \{a, c\}\), \(e_2 = \{b, d\}\), \(e_3 = \{c, d\}\), \(e_4 = \{c, e\}\), \(e_5 = \{d, e\}\), and \(e_6 = \{e, e\}\).
- Let \(G\) be defined by \(V = \{a, b, c\}\) and \(E = \{e_1, e_2, e_3\}\) with \(e_1 = \{a, b\}\), \(e_2 = \{a, c\}\), and \(e_3 = \{a, c\}\).
- Let \(G\) be defined by \(V = \{a, b, c, d\}\) and \(E = \{e_1, e_2, e_3\}\) with \(e_1 = \{a, b\}\), \(e_2 = \{a, c\}\), and \(e_3 = \{b, c\}\).
Exercise \(\PageIndex{2}\)
- Let \(G\) be the graph whose vertices are the \(2\)-element subsets of \(\{1, 2, 3, 4, 5\}\), with vertices \(\{a, b\}\) and \(\{c, d\}\) adjacent if and only if \(\{a, b\} ∩ \{c, d\} = ∅\). Draw \(G\).
- The number of edges in the \(k\)-dimensional cube \(Q_k\) (which is an important structure in network design, but you do not need to know the structure to solve this) can be found by the recurrence relation:
\(e(Q_0) = 0; e(Q_n) = 2e(Q_{n−1}) + 2^{n−1}\) for \(n ≥ 1\).
Use generating functions to solve this recurrence relation and therefore determine the number of edges in the \(k\)-dimensional cube


