11.3: Deletion, Complete Graphs, and the Handshaking Lemma

Last updated
Save as PDF

Page ID: 60129

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

We’ll begin this section by introducing a basic operation that can change a graph (or a multigraph, with or without loops) into a smaller graph: deletion.

Definition: Vertex Deletion

Start with a graph (or multigraph, with or without loops) $G$ with vertex set $V$ and edge set $E$, and some vertex $v ∈ V$. If we delete the vertex $v$ from the graph $G$, the resulting graph has vertex set $V \setminus \{v\}$ and edge set

\[E \setminus \{e | e \text{ is incident with } v\}.\]

Notation

The graph obtained by deleting the vertex $v$ from $G$ is denoted by $G \setminus \{v\}$. We can delete more than one vertex; for any set $S ⊆ V$ of vertices of $G$, we use $G \setminus S$ to denote the graph obtained by deleting all of the vertices of $S$ from $G$.

The graph $G \setminus \{v\}$ might be a multigraph, but only if $G$ is. It could have loops, but only if $G$ has loops.

If we begin with the graph

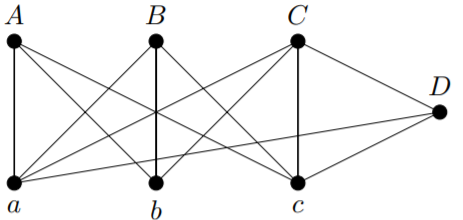
$clipboard_e12f51aab5e48ecbef92186e86f2688f2.png$

and delete the vertex $D$, then we obtain the graph shown in Figure 11.2.2.

We can also delete edges, rather than vertices.

Definition: Edge Deletion

Start with a graph (or multigraph, with or without loops) $G$ with vertex set $V$ and edge set $E$, and some edge $e ∈ E$. If we delete the edge $e$ from the graph $G$, the resulting graph has vertex set $V$ and edge set $E \setminus \{e\}$.

Vertex and edge deletion will be very useful for using proofs by induction on graphs (and multigraphs, with or without loops). It is handy to have terminology for a graph that can be obtained from another graph by deleting vertices and/or edges.

Notation

The graph obtained by deleting the edge $e$ from $G$ is denoted by $G \setminus {e}$. We can delete more than one edge; for any set $T ⊆ E$ of edges of $G$, we use $G \setminus T$ to denote the graph obtained by deleting all of the edges of $T$ from $G$.

The graph $G \setminus \{e\}$ might be a multigraph, but only if $G$ is. It could have loops, but only if $G$ has loops.

Notice that deleting the edges $\{C, D\}$, $\{a, D\}$ and $\{c, D\}$ from the graph drawn above, does not result in the graph shown in Figure 11.2.2, because the graph we obtain by deleting these edges still has the vertex $D$ (as an isolated vertex), whereas the graph shown in Figure 11.2.2 has only the six vertices $\{a, b, c, A, B, C\}$.

Definition: Subgraph

Let $G$ be a graph. If $H$ can be obtained from $G$ by deleting vertices and/or edges, then $H$ is a subgraph of $G$. A subgraph $H$ of $G$ is proper if $H \neq G$.

We now define a very important family of graphs, called complete graphs.

Definition: Complete Graph

A (simple) graph in which every vertex is adjacent to every other vertex, is called a complete graph. If this graph has $n$ vertices, then it is denoted by $K_n$.

The notation $K_n$ for a complete graph on $n$ vertices comes from the name of Kazimierz Kuratowski, a Polish mathematician who lived from 1896–1980. Although his main area of research was logic, Kuratowski proved an important theorem that involves a complete graph. We’ll study his theorem later in the course.

With this setup, we are ready to prove our first result about graphs.

Proposition $\PageIndex{1}$

The number of edges of $K_n$ is $\dfrac{n(n−1)}{2} = \binom{n}{2}$

We present two proofs of this proposition: first, a combinatorial proof; then, a proof by induction

Proof

1) Combinatorial Proof: A complete graph has an edge between any pair of vertices. From n vertices, there are $\binom{n}{2}$ pairs that must be connected by an edge for the graph to be complete. Thus, there are $\binom{n}{2}$ edges in $K_n$.

Before giving the proof by induction, let’s show a few of the small complete graphs. In particular, we’ll need to have $K_1$ in mind as it will be the base case for our induction.

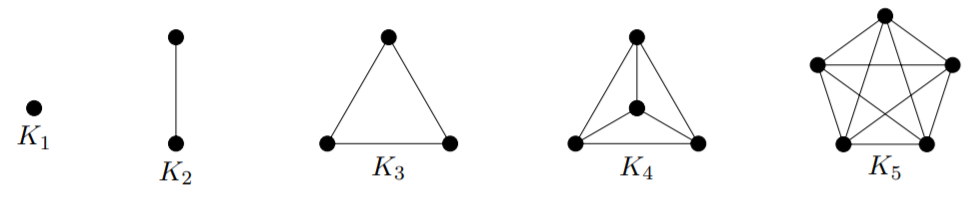
$clipboard_e01137f0e1224b6424dc16e61d5864afe.png$

2) Proof By Induction: Base case: $n = 1$. As we can see above, the graph $K_1$ has $0$ edges. Also,

$\dfrac{n(n−1)}{2} = \dfrac{1(0)}{2} = 0 $

So the equality holds for $n = 1$. This completes the proof of the base case.

Inductive step: We begin with the inductive hypothesis. Let $k ≥ 1$ be arbitrary, and suppose that $K_k$ has $\binom{k}{2}$ edges.

We want to deduce that $K_{k+1}$ has $\binom{k+1}{2}$ edges. Start with $K_{k+1}$, and let the number of edges of this graph be $t$. Now we delete a vertex $v$ from $K_{k+1}$. By the definition of vertex deletion, we must delete every edge incident with $v$. Since $K_{k+1}$ is complete, $v$ is adjacent to every other vertex, so there are $k$ edges incident with $v$, and it is precisely these edges that we have deleted. There must be $t − k$ edges remaining.

Notice that deleting $v$ does not affect edges that are not incident with $v$. Therefore, if we consider any two vertices in the remaining graph, they will still be adjacent (since they were adjacent in $K_{k+1}$ and the edge between them was not deleted). Thus, the remaining graph is $K_k$.

Using our inductive hypothesis, we know that $K_k$ has $\dfrac{k(k − 1)}{2}$ edges. We have shown that $t − k = \dfrac{k(k − 1)}{2}$, so

$t = \dfrac{k(k − 1)}{2} + k = k \left( \dfrac{(k-1)}{2} + 1 \right) = \dfrac{k(k + 1)}{2} = \binom{k+1}{2} $

which is what we wanted to deduce. This completes the proof of the inductive step.

By the Principle of Mathematical Induction, $K_n$ has $\binom{n}{2}$ vertices for every $n ≥ 1$.

Although this proof by induction may seem ridiculously long and complicated in comparison with the combinatorial proof, it serves as a relatively simple illustration of how proofs by induction can work on graphs. This can be a very powerful technique for proving results about graphs.

Here is another result that can be proven using either a combinatorial proof, or a proof by induction.

Lemma $\PageIndex{1}$: Euler's Handshaking Lemma

For any graph (or multigraph, with or without loops).

\[\sum_{v∈V} d(v) = 2|E| \]

This is called the handshaking lemma because it is often explained using vertices to represent people, and edges as handshakes between people. In this explanation, the lemma says that if you add up all of the hands shaken by all of the people, you will get twice the number of handshakes that took place. This is an example of using two ways to count pairs $(v, e) ∈ V \times E$ such that $v$ is incident with $e$, a notion that we discussed briefly when we introduced combinatorial proofs.

Proof: For the left-hand side of the equation, at every vertex we count the number of edges incident with that vertex. To get the right-hand side from this, observe that this process results in every edge having been counted exactly twice (once at each of its two endvertices; or, in the case of a loop, twice at its single endvertex since both ends are there).

Although from the right perspective the handshaking lemma might seem obvious, it has a very important and useful corollary.

Corollary $\PageIndex{1}$

Every graph has an even number of vertices of odd valency.

Proof: Since the sum of all of the valencies in the graph is even (by Euler’s handshaking lemma, Lemma 11.3.1), the number of odd summands in this sum must be even. That is, the number of vertices that have odd valency must be even.

Exercise $\PageIndex{1}$

Give a proof by induction of Euler’s handshaking lemma for simple graphs.
Draw $K_7$.
Show that there is a way of deleting an edge and a vertex from $K_7$ (in that order) so that the resulting graph is complete. Show that there is a way of deleting an edge and a vertex from $K_7$ (in that order) so that the resulting graph is not complete.
Prove Corollary 11.3.1 by induction on the number of edges. (Use edge deletion, and remember that the base case needs to be when there are no edges.)
Use graphs to give a combinatorial proof that

$\sum_{i=1}^{k} \binom{n_i}{2} ≤ \binom{n}{2} $

where $n_1, n_2, . . . , n_k$ are positive integers with $\sum_{i=1}^{k} n_i = n$. Under what circumstances does equality hold?