13.1: Euler Tours and Trails

Last updated
Save as PDF

Page ID: 60138

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

To introduce these concepts, we need to know about some special kinds of walks.

Definition: Special Kinds of Works

A walk is closed if it begins and ends with the same vertex.
A trail is a walk in which no two vertices appear consecutively (in either order) more than once. (That is, no edge is used more than once.)
A tour is a closed trail.
An Euler trail is a trail in which every pair of adjacent vertices appear consecutively. (That is, every edge is used exactly once.)
An Euler tour is a closed Euler trail.

Recall the historical example of the bridges of Königsberg. The problem of finding a route that crosses every bridge exactly once, is equivalent to finding an Euler trail in the corresponding graph. If we want the route to begin and end at the same place (for example, someone’s home), then the problem is equivalent to finding an Euler tour in the corresponding graph.

Euler tours and trails are important tools for planning routes for tasks like garbage collection, street sweeping, and searches.

Example $\PageIndex{1}$

In the graph

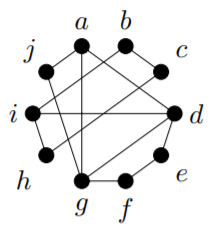
$clipboard_e3cd58b54ec3a63d6d80d1c8521bd96d7.png$

$(i, b, c, h, i, d, e, f, g, d, a, g, j, a)$ is an Euler trail. In the graph

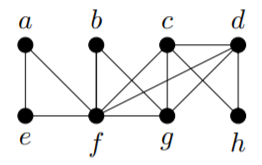
$clipboard_e02e0cfb483c7c7c0bc2b01885cf4a1b8.png$

$(a, e, f, b, g, f, c, d, h, c, g, d, f, a)$ is an Euler tour.

Here is Euler’s method for finding Euler tours. We will state it for multigraphs, as that makes the corresponding result about Euler trails a very easy corollary.

Theorem $\PageIndex{1}$

A connected graph (or multigraph, with or without loops) has an Euler tour if and only if every vertex in the graph has even valency.

Proof

As the statement is if and only if, we must prove both implications.

\((⇒) Suppose we have a multigraph (possibly with loops) that has an Euler tour,

\[(u_1, u_2, . . . , u_{e+1} = u_1),\]

where $e = |E|$. Let $u$ be an arbitrary vertex of the multigraph. Every time $u$ appears in the tour, exactly two of the edges incident with $u$ are used: if $u = u_j$, then the edges used are $u_{j−1}u_j$ and $u_ju_{j−1}$ unless $j = 1$ or $j = e + 1$ in which case $u = u_1 = u_{e+1}$ and the edges are $u_eu$ and $uu_2$ (and we consider this as one appearance of u in the tour). Therefore, if $u$ appears $k$ times in the tour, then since by the definition of an Euler tour all edges incident with $u$ are used exactly once, we conclude that $u$ must have valency $2k$. Since $u$ was an arbitrary vertex of the multigraph and $k$ (the number of times $u$ appears in the tour) must be an integer, this shows that the valency of every vertex must be even.

$(⇐)$ Suppose we have a connected multigraph in which the valency of every vertex is even. Consider the following algorithm (which will be the first stage of our final algorithm):

Make $u$ (some arbitrary vertex) our active vertex, with a list $L$ of all of the edges of $E$. Make $u$ the first vertex in a new sequence $C$ of vertices. Repeat the following step as many times as possible:

Call the active vertex $v$. Choose any edge $vx$ in $L$ that is incident with $v$. Add $x$ (the other endvertex of this edge) to the end of $C$, and make $x$ the new active vertex. Remove $vx$ from $L$.

We claim that when this algorithm terminates, the sequence $C$ will be a tour (though not necessarily an Euler tour) in the multigraph. By construction, $C$ is a walk, and $C$ cannot use any edge more than once since each edge appears in $L$ only once and is removed from $L$ once it has been used, so $C$ is a trail. We need to show that the walk $C$ is closed.

The only way the algorithm can terminate is if $L$ contains no edge that is incident with the active vertex. Towards a contradiction, suppose that this happens at a time when the active vertex is $y \neq u$. Now, $y$ has valency $2r$ in the multigraph for some integer $r$, so there were $2r$ edges in $L$ that were incident with $y$ when we started the algorithm. Since $y \neq u$, every time $y$ appears in $C$ before this appearance, we removed $2$ edges incident with $y$ from $L$ (one in the step when we made $y$ the active vertex, and one in the following step). Furthermore, we removed one additional edge incident with $y$ from $L$ in the final step, when we made $y$ the active vertex again. Thus if there are $t$ previous appearances of $y$ in $C$, we have removed $2t + 1$ edges incident with $y$ from $L$. Since $2r$ is even and $2t+ 1$ is odd, there must still be at least one edge incident with $y$ that is in $L$, contradicting the fact that the algorithm terminated. This contradiction shows that, when the algorithm terminates, the active vertex must be $u$, so the sequence $C$ is a closed walk. Since $C$ is a trail, we see that $C$ must be a tour.

If the tour $C$ is not an Euler tour, let $y$ be the first vertex that appears in $C$ for which there remains an incident edge in $L$. Repeat the previous algorithm starting with $y$ being the active vertex, and with $L$ starting at its current state (not all of $E$). The result will be a tour beginning and ending at y that uses only edges that were not in $C$. Insert this tour into $C$ as follows: if $C = (u = u_1 . . . , y = u_i , . . . , u_k = u)$ and the new tour is $(y = v_1, . . . , v_j = y)$, then the result of inserting the new tour into $C$ will be

\[(u = u_1, . . . , y = u_i = v_1, v_2, . . . , v_j = y = u_i , u_{i+1}, . . . , u_k = u).\]

Replace $C$ by this extended tour.

Repeat the process described in the previous paragraph as many times as possible (this is the second and last stage of our final algorithm). Since $E$ is finite and the multigraph is connected, sooner or later all of the edges of $L$ must be exhausted. At this point, we must have an Euler tour.

Example $\PageIndex{2}$

Use the algorithm described in the proof of the previous result, to find an Euler tour in the following graph.

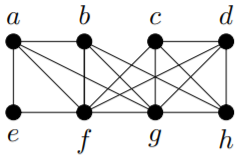
$clipboard_e84ae166bb6b63fa2823d3add61f6d47e.png$

Solution

Let’s begin the algorithm at $a$. As $E = L$ is a large set, we won’t list the remaining elements every time we choose a new active vertex in the early stages. An easy method for you to keep track of the edges still in $L$ is to colour the edges that are no longer in $L$ (the edges we use) with a different colour as we go.

There are many different possible outcomes for the algorithm since there are often many acceptable choices for the next active vertex. One initial set of choices could be

$C = (a, b, f, e, a, f, g, a).$

The first stage of the algorithm terminates at this point since all four edges incident with $a$ have been used. At this point, we have

$L = \{bg, bh, cd, cf, cg, ch, df, dg, dh, gh\}.$

The first vertex in $C$ that is incident with an edge in $L$ is $b$. We run the first stage of the algorithm again with $b$ as the initial active vertex and this list for $L$. Again, there are many possible outcomes; one is $(b, g, h, b)$.

We insert $(b, g, h, b)$ into $C$, obtaining a new $C = (a, b, g, h, b, f, e, a, f, g, a)$. At this point, we have

$L = \{cd, cf, cg, ch, df, dg, dh\}.$

Now $g$ is the first vertex in $C$ that is incident with an edge in $L$. We run the first stage of the algorithm again with $g$ as the initial active vertex and the current $L$. One possible outcome is $(g, c, f, d, g)$.

Inserting this into $C$ yields a new

$C = (a, b, g, c, f, d, g, h, b, f, e, a, f, g, a).$

At this point, we have $L = \{cd, ch, dh\}$. The first vertex in $C$ that is incident with an edge in $L$ is $c$. We run the first stage of the algorithm one final time with $c$ as the initial active vertex and $L = \{cd, ch, dh\}$. This time there are only two possible outcomes: $(c, d, h, c)$ or $(c, h, d, c)$. We choose $(c, d, h, c)$.

Inserting this into $C$ yields our Euler tour:

$C = (a, b, g, c, d, h, c, f, d, g, h, b, f, e, a, f, g, a).$

Corollary $\PageIndex{1}$

A connected graph (or multigraph, with or without loops) has an Euler trail if and only if at most two vertices have odd valency.

Proof

Suppose we have a connected graph (or multigraph, with or without loops), $G$. Since the statement is if and only if, there are two implications to prove.

$(⇒)$ Suppose that $G$ has an Euler trail. If the trail is closed then it is a tour, and by Theorem 13.1.1, there are no vertices of odd valency. If the trail is not closed, say it is a $u − v$ walk. Add an edge between $u$ and $v$ to $G$, creating a new graph $G^∗$ (note that $G^∗$ may be a multigraph if $uv$ was already an edge of $G$, even if $G$ wasn’t a multigraph), and add $u$ to the end of the Euler trail in $G$, to create an Euler tour in $G^∗$. By Theorem 13.1.1, the fact that $G^∗$ has an Euler tour means that every vertex of $G^∗$ has even valency. Now, the vertices of $G$ all have the same valency in $G^∗$ as they have in $G$, with the exception that the valencies of $u$ and $v$ are one higher in $G^∗$ than in $G$. Therefore, in this case there are exactly two vertices of odd valency in $G$; namely, $u$ and $v$.

$(⇐)$ Now we suppose that $G$ has at most $2$ vertices of odd valency. By Corollary 11.3.1 (the corollary to Euler’s handshaking lemma), if there are at most two vertices of odd valency, then there are either $0$ or $2$ vertices of odd valency. We consider these two cases.

If there are $0$ vertices of odd valency, then by Theorem 13.1.1, $G$ has an Euler tour.

If there are two vertices of odd valency, say $u$ and $v$, add an edge between $u$ and $v$ to $G$, creating a new graph $G^∗$ (note that $G^∗$ may be a multigraph if $uv$ was already an edge of $G$, even if $G$ wasn’t a multigraph). Now in $G^∗$ every vertex has even valency, so $G^∗$ has an Euler tour. In fact, a careful look at the algorithm given in the proof of Theorem 13.1.1 shows that we may choose $u$ and $v$ (in that order) to be the first two vertices in this Euler tour, so that $uv$ (the edge that is in $G^∗$ but not $G$) is the first edge used in the tour. Now if we delete $u$ from the start of this Euler tour, the result is an Euler trail in $G$ that starts at $v$ and ends at $u$.

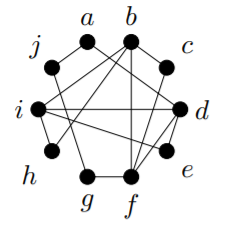
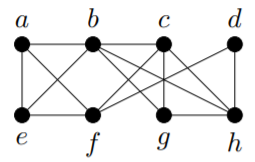
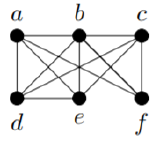
Exercise $\PageIndex{1}$

For each of the following graphs, is there an Euler tour? Is there an Euler trail? If either exists, find one; if not, explain why not.

1) $clipboard_e04a984a60fcc07768fbca28bc192555f.png$

2) $clipboard_e18c4f00db6996c9494e395719a293956.png$

3) $clipboard_e1a2e43eefd75f4509db7865025f31d16.png$

4) If it is possible, draw a graph that has an even number of vertices and an odd number of edges, that also has an Euler tour. If that isn’t possible, explain why there is no such graph.

5) Which complete graphs have an Euler tour? Of the complete graphs that do not have an Euler tour, which of them have an Euler trail?

Exercise $\PageIndex{2}$

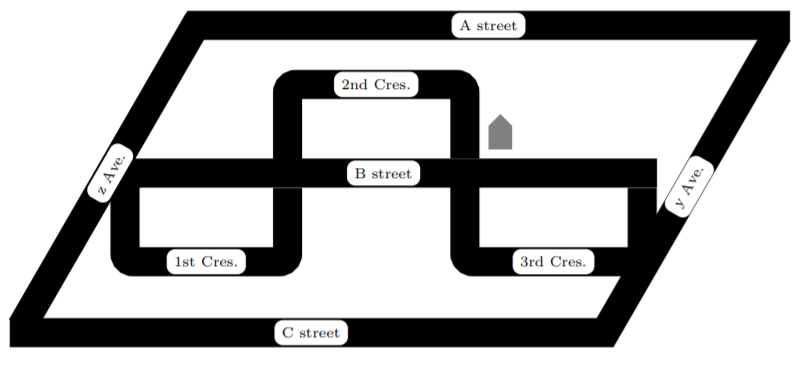
Sylvia’s cat is missing. She wants to look for it in all the nearby streets, but she is tired and doesn’t want to walk any farther than she must. Find an efficient route for Sylvia to take through her neighbourhood so that she starts and ends at home and walks through each street exactly once. The location of Sylvia’s house is marked with a house-shaped symbol ( $clipboard_e0c4a6e4818032f2055d6be635c0cc852.png$ ).

$clipboard_e48652834b9e6ce5d6af5703579b98f29.png$