9.4: Complement, union, and intersection

First, it is often convenient to restrict the scope of the discussion.

Definition: Universal set

a set that contains all objects currently under consideration

We will consider all of the following set operations to be performed within a universal set \(U\text{.}\) In particular, suppose \(A,B\subseteq U\text{.}\)

9.4.1: Universal and relative complement

Definition: Complement

the set of elements of \(U\) which are not in \(A\)

Definition: \(A^{C}\)

the complement of \(A\) (in \(U\)), so that

\begin{equation*} A^{C} = \{ x \in U \vert x \notin A \} \end{equation*}

Definition: Relative complement

if \(A,B \subseteq U\text{,}\) the complement of \(A\) in \(B\) is the set of elements of \(B\) which are not in \(A\)

Definition: \(B \setminus A\)

the complement of \(A\) in \(B\text{,}\) so that

\begin{equation*} B \setminus A = \{ x \in B \vert x \notin A \} \end{equation*}

Figure \(\PageIndex{1}\): Venn diagrams of universal and relative set complements.

 

 

Note \(\PageIndex{1}\)

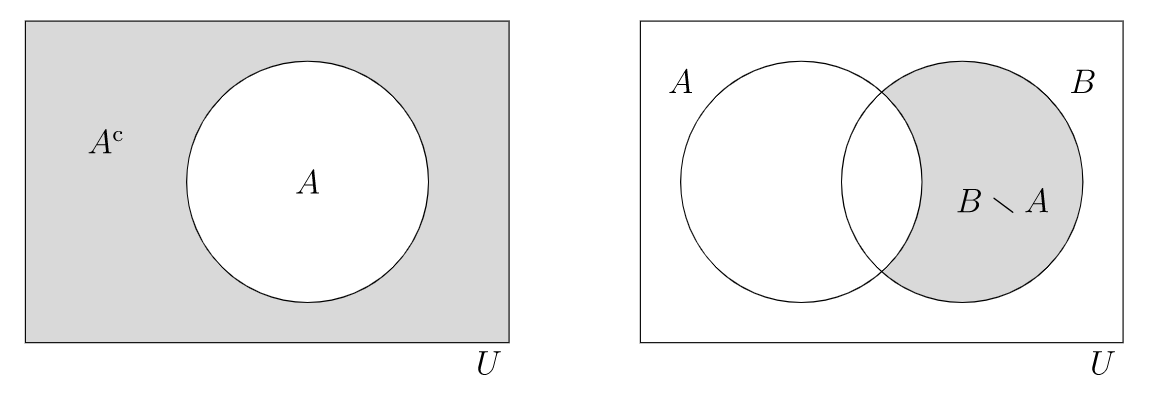
Another common notation for relative complement is \(B - A\text{.}\) However, this conflicts with the notation for the algebraic operation of subtraction in certain contexts, so we will prefer the notation \(B \setminus A\text{.}\)

Example \(\PageIndex{1}\): Some examples of relative complement involving number sets

• Suppose \(B = \{ 1, 2, 3, 4, 5, 6 \}\) and \(A = \{ 1, 3, 5 \}\text{.}\) Then \(B \setminus A = \{ 2, 4, 6 \}\text{.}\)
• The complement of the set of rational numbers \(\mathbb{Q}\) inside the set of real numbers \(\mathbb{R}\) is called the set of irrational numbers, and we write \(\mathbb{I} = \mathbb{R} \setminus \mathbb{Q} \) for this set. If you are thinking of real numbers in terms of their decimal expanions, the irrational numbers are precisely those that have nonterminating, nonrepeating decimal expansions.

9.4.2: Union, intersection, and disjoint sets

Definition: Union

the combined collection of all elements in a pair of sets

Definition: \(A \cup B\)

the union of sets \(A\) and \(B\text{,}\) so that

\begin{equation*} A \cup B = \{ x\in U \vert x\in A \text{ or } x\in B \text{ (or both)}\} \end{equation*}

Definition: Intersection

the collection of only those elements common to a pair of sets

Definition: \(A \cap B\)

the intersection of \(A\) and \(B\text{,}\) so that

\begin{equation*} A \cap B = \{x\in U \vert x\in A \text{ and } x\in B \} \end{equation*}

Figure \(\PageIndex{1}\): Venn diagrams of set union and intersection.

Note \(\PageIndex{2}\)

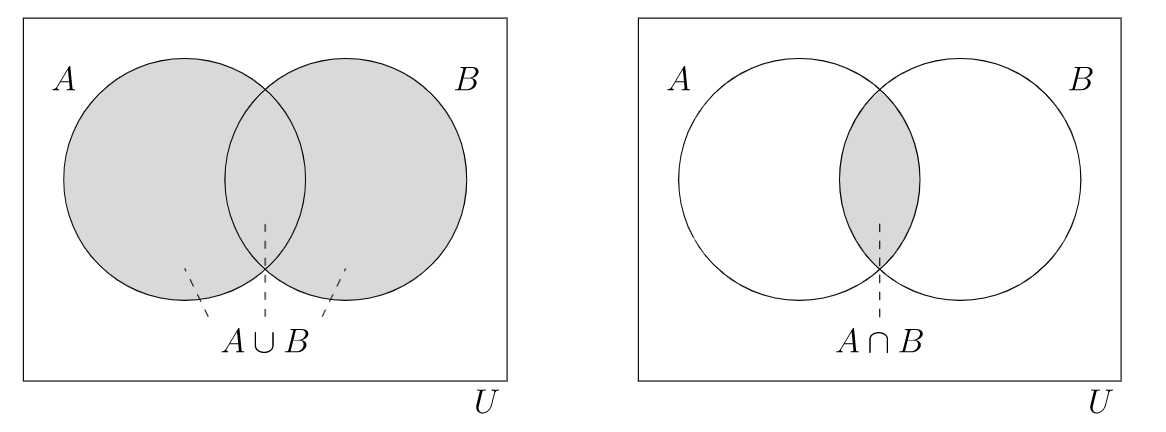
A union contains every element from both sets, so it contains both sets as subsets:

\begin{equation*} A, B \subseteq A \cup B \text{.} \end{equation*}

On the other hand, every element in an intersection is in both sets, so the intersection is a subset of both sets:

\begin{equation*} A \cap B \subseteq A, B \text{.} \end{equation*}

Example \(\PageIndex{2}\)

For subsets \(A = \{1,2,3,4\}\) and \(B = \{3,4,5,6\}\) of \(\mathbb{N}\text{,}\) we have

\begin{align*} A \cup B & = \{1,2,3,4,5,6\}, & A \cap B & = \{3,4\}. \end{align*}

Example \(\PageIndex{3}\)

Consider the following subsets of \(\mathbb{N}\text{.}\)

\begin{align*} \scr{E} & = \{ n\in\mathbb{N} \vert n\text{ even}\} & \scr{P} & = \{n\in\mathbb{N} \vert n\text{ prime, } n\mathbb{N}e 0\} \\ \scr{O} & = \{ n\in\mathbb{N} \vert n\text{ odd} \} & \scr{T} & = \{3n \vert n\in\mathbb{N} \} = \{ 0,\, 3,\, 6,\, 9,\, \ldots \} \end{align*}
Then,

\begin{align*} \scr{E} \cup\scr{O} & = \mathbb{N}, & \scr{E} \cap \scr{P} & = \{2\}, & \scr{E} \cap \scr{T} & = \{6n \vert n\in\mathbb{N} \}, \\ \scr{E} \cap \scr{O} & = \emptyset, & \scr{O} \cap \scr{P} & = \scr{P} \setminus \{2\}, & \scr{O} \cap \scr{T} & = \{6n+3 \vert n\in\mathbb{N}\}. \end{align*}

Definition: Disjoint Sets

sets that have no elements in common, i.e. sets \(A,B\) such that \(A\cap B = \emptyset\)

Definition: Disjoint Union

a union \(A \cup B\) where \(A\) and \(B\) are disjoint

Definition: \(A \sqcup B\)

the disjoint union of sets \(A\) and \(B\)

Figure \(\PageIndex{2}\): A Venn diagram of a disjoint set union.

Example \(\PageIndex{4}\)

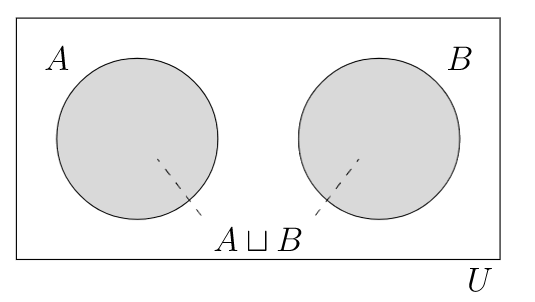
Sets \(\scr{E},\scr{O}\) from Example \(\PageIndex{3}\) are disjoint, and \(\mathbb{N} = \scr{E} \sqcup \scr{O}\text{.}\)

Remark \(\PageIndex{1}\)

If \(A \subseteq U\text{,}\) then we can express \(U\) as a disjoint union \(U = A \sqcup A^{C}\text{.}\) Similarly, if \(U = A \sqcup B\text{,}\) then we must have \(B = A^{C}\text{.}\)

9.4.3: Rules for set operations

Proposition \(\PageIndex{1}\): Rules for Operations on Sets

Suppose \(A,B,C\) are subsets of a universal set \(U\text{.}\) Then the following set equalities hold.

1. Properties of the universal set.
   1. \(\displaystyle A \cup U = U \)
   2. \(\displaystyle A \cap U = A \)
2. Properties of the empty set.
   1. \(\displaystyle A \cup \emptyset = A \)
   2. \(\displaystyle A \cap \emptyset = \emptyset \)
3. Duality of universal and empty sets.
   1. \(\displaystyle U^{C} = \emptyset \)
   2. \(\displaystyle \emptyset ^{C} = U \)
4. \(\displaystyle (A^{C})^C = A \)
5. Idempotence.
   1. \(\displaystyle A \cup A = A \)
   2. \(\displaystyle A \cap A = A \)
6. Commutativity.
   1. \(\displaystyle A \cup B = B \cup A \)
   2. \(\displaystyle A \cap B = B \cap A \)
7. Associativity.
   1. \(\displaystyle (A \cup B) \cup C = A \cup (B \cup C) \)
   2. \(\displaystyle (A \cap B) \cap C = A \cap (B \cap C) \)
8. Distributivity.
   1. \(\displaystyle A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
   2. \(\displaystyle A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
   3. \(\displaystyle (A \cup B) \cap C = (A \cap C) \cup (B \cap C) \)
   4. \(\displaystyle (A \cap B) \cup C = (A \cup C) \cap (B \cup C) \)
9. DeMorgan's Laws.
   1. \(\displaystyle (A \cup B)^C = A^{C} \cap B^C \)
   2. \(\displaystyle (A \cap B)^C = A^{C} \cup B^C \)

 

Proof of Rule 9.a.

Recall that to prove this set equality, we need to show both

\begin{align*} (A \cup B)^C & \subseteq A^{C} \cap B^C \text{,} & A^{C} \cap B^C & \subseteq (A \cup B)^C \text{.} \end{align*}

Show \((A \cup B)^C \subseteq A^{C} \cap B^C\).
We need to show

\begin{equation*} x \in (A \cup B)^C \Rightarrow x \in A^{C} \cap B^C \text{.} \end{equation*}

If \(x \in (A \cup B)^C\) then by definition of complement, \(x\in U\) but \(x \notin A \cup B\text{.}\) Then \(x \notin A\) must be true, since if \(x\) were in \(A\) then it would also be in \(A \cup B\text{.}\) Similarly, \(x \notin B\) must also be true. So \(x \in A^{C}\) and \(x\in B^C\text{;}\) i.e. \(x\in A^{C} \cap B^C\text{.}\)

Show \(A^{C} \cap B^C \subseteq (A \cup B)^C \). We need to show

\begin{equation*} x \in A^{C} \cap B^C \Rightarrow x \in (A \cup B)^C \text{.} \end{equation*}

If \(x \in A^{C} \cap B^C\) then by definition of intersection, both \(x \in A^{C}\) and \(x \in B^C\) are true.; i.e. \(x \notin A\) and \(x \notin B\text{.}\) Since \(A \cup B\) is all elements of \(U\) which are in one (or both) of \(A,B\text{,}\) we must have \(x \notin A \cup B\text{.}\) Thus \(x \in (A \cup B)^C\text{.}\)

Proofs of the other rules.

These are left to you, the reader, in the Exercise 9.9.1.

 

Remark \(\PageIndex{2}\)

Compare the set operation rules of the proposition above with the Rules of Propositional Calculus.