3.5.7: The Coefficient of Drag
- Page ID
- 103782
WE HAVE SEEN THAT AIR DRAG can play a role in interesting physics problems in differential equations. This also is an important concept in fluid flow and fluid mechanics when looking at flows around obstacles, or when the obstacle is moving with respect to the background fluid. The simplest such object is a sphere, such as a baseball, soccer ball, golf ball, or ideal spherical raindrop. The resistive force is characterized by the dimensionless drag coefficient
\[C_{D}=\dfrac{F_{D}}{\dfrac{1}{2} \rho U^{2} L^{2}}\nonumber \]
where \(L\) and \(U\) are the characteristic length and speed of the object moving through the fluid.
There has been much attention focussed on relating the drag coefficient to the Reynolds number. The Reynolds number is given by
\[R e=\dfrac{\rho L U}{\eta}=\dfrac{L V}{v}\nonumber \]
where \(\eta\) is the viscosity and \(v=\dfrac{\eta}{\rho}\) is the kinematic viscosity. It is a measure of the size of the kinematic to viscous forces in the problem at hand. There are different ranges of fluid behavior depending on the order of the Reynolds number. These range from laminar flow \((R e<1000)\) to turbulent flow \(\left(\operatorname{Re}>2.5 \times 10^{5}\right)\). There are a range of other types of flows such as creeping flow \((\mathrm{Re}<<1)\) and transitional flows, which are a mix of laminar and turbulent flow.
For low Reynolds number, the inertial forces are small compared to the viscous forces, leading to the Stokes drag force, \(C_{D}=24 R e^{-1}\). This result can be determined analytically. Similarly, for large Reynolds number the drag coefficient is a constant. This is the Newtonian regime. Somewhere in between the form of the drag coefficient is found through empirical studies. There have been many empirical expressions developed and all are within a few percent of the data in the range of applicability. Some of the commonly used expressions are given below.
Models that are useful for \(R e<10^{3}:\)
\[C_{2} =\dfrac{24}{R e}+\dfrac{4}{R e^{1 / 3}}, \quad \text{ Putnam }(1961) \nonumber \]
\[C_{3}=\dfrac{24}{R e}\left(1+0.15 R e^{0.687}\right), \quad \text{ Schiller-Naumann }(1933), \nonumber \]
\[C_{4} =12 R e^{-.5} ; \quad \text{ Edwards et al. }(2000), \nonumber \]
Models that are useful for \(R e<2 \times 10^{5}\) are the White (1991) and CliftGavin (1970), respectively,
\[C_{1} =\dfrac{24}{R e}+\dfrac{6 .}{1+\sqrt{R e}}+0.4 \nonumber \]
\[C_{5} =\dfrac{24}{R e}\left(1+0.15 R e^{0.687}\right)+\dfrac{.42}{1+42500 / R e^{1.16}} \nonumber \]
A more recent model was proposed by Morrison (2010) for \(R e<10^{6}:\)
\[C_{6}=\dfrac{24}{R e}+\dfrac{2.6\left(\dfrac{R e}{5.0}\right)}{1+\left(\dfrac{R e}{5.0}\right)^{1.52}}+\dfrac{.411\left(\dfrac{R e}{263000}\right)^{-7.94}}{1+\left(\dfrac{R e}{263000}\right)^{-8.00}}+\dfrac{R e^{0.80}}{461000} \nonumber \]
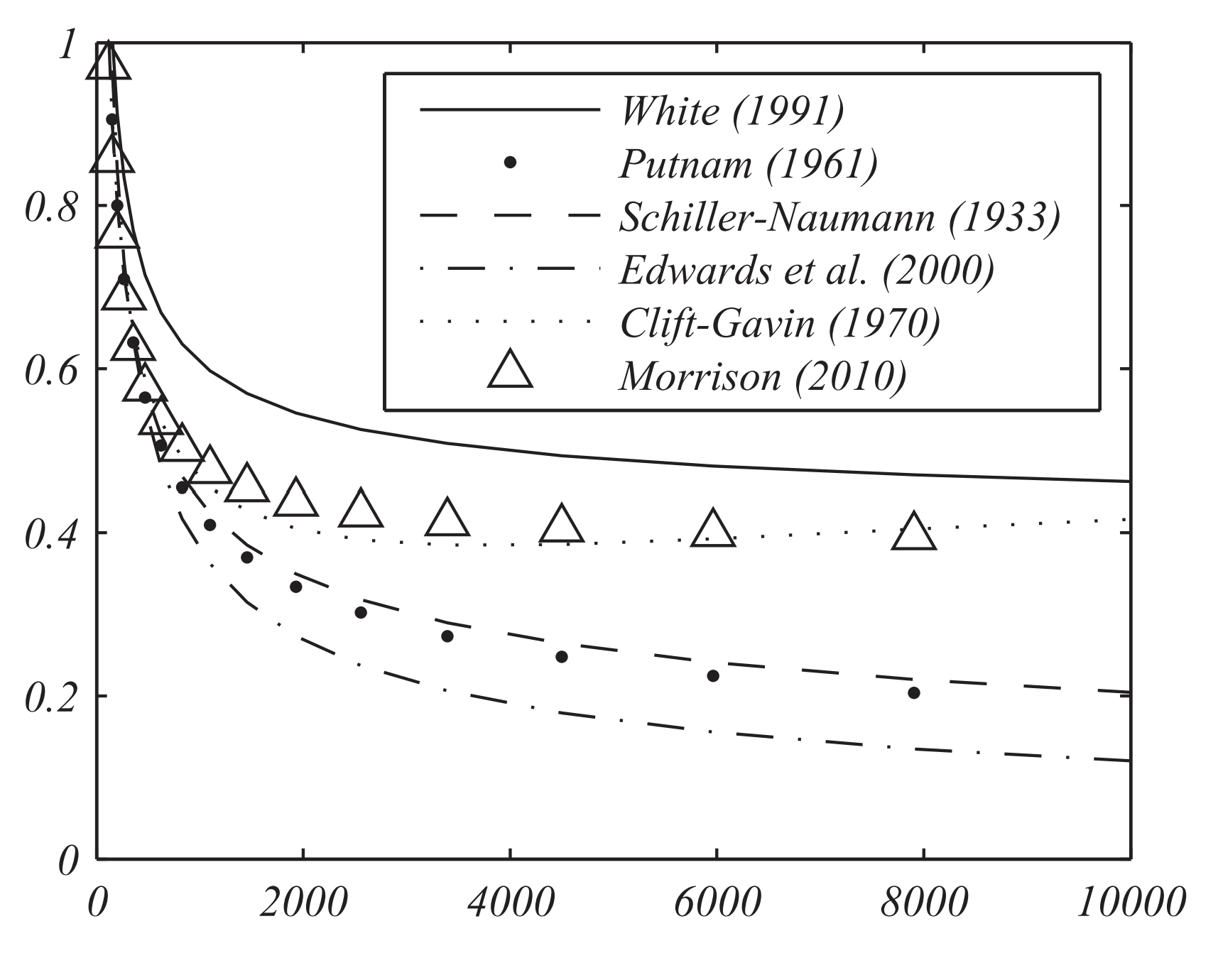
Plots for these models are shown in Figures \(\PageIndex{1} - \PageIndex{2}\). In Figure \(\PageIndex{1}\) we see that the models differ significantly for large Reynolds numbers.
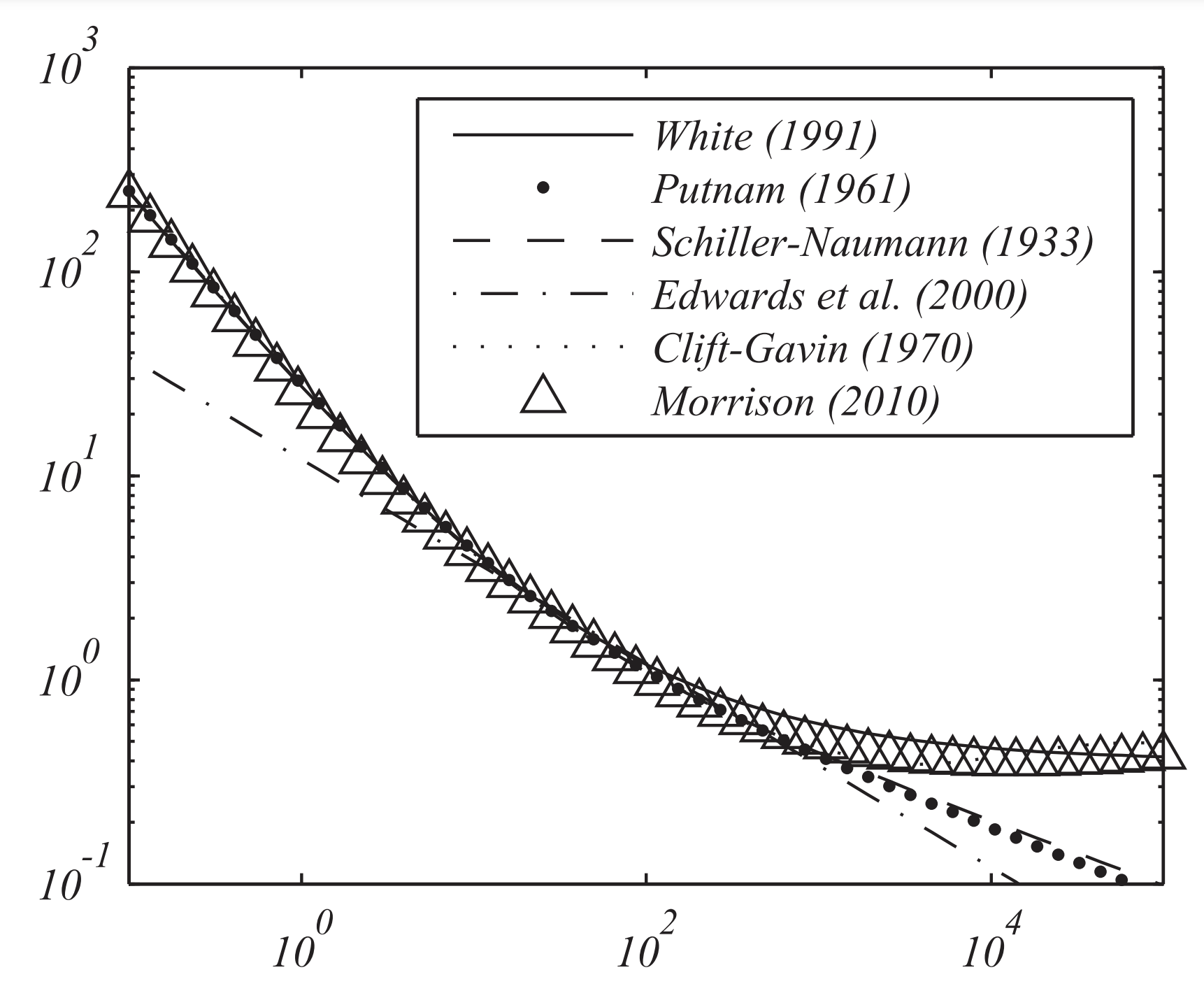
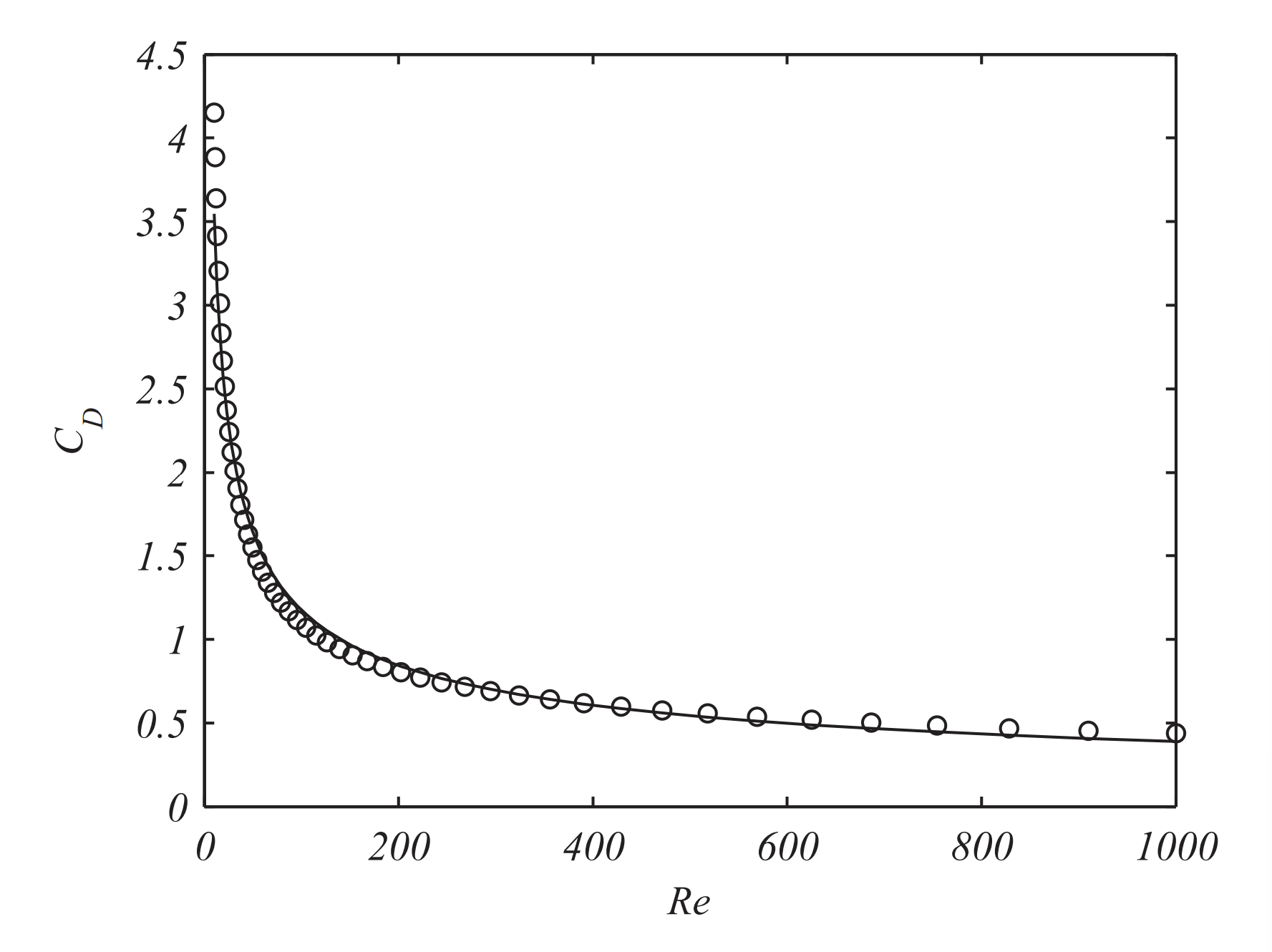
Figure \(\PageIndex{2}\) shows a log-log plot of the drag coefficient as a function of Reynolds number. In Figure \(\PageIndex{3}\) we show a power law fit for Reynolds number less than 1000 confirming the model used by Edwards, Wilder, and Scime (2001) as described in the raindrop problem.