3.8: Limit Cycles

So far we have just been concerned with equilibrium solutions and their behavior. However, asymptotically stable fixed points are not the only attractors. There are other types of solutions, known as limit cycles, towards which a solution may tend. In this section we will look at some examples of these periodic solutions.

Such solutions are common in nature. Rayleigh investigated the problem

\[x'' + c \left( \dfrac{1}{3} (x')^2 - 1 \right) x' + x = 0 \label{3.38} \]

in the study of the vibrations of a violin string. Van der Pol studied an electrical circuit, modelling this behavior. Others have looked into biological systems, such as neural systems, chemical reactions, such as Michaelis-Menton kinetics or systems leading to chemical oscillations. One of the most important models in the historical study of dynamical systems is that of planetary motion and investigating the stability of planetary orbits. As is well known, these orbits are periodic.

Limit cycles are isolated periodic solutions towards which neighboring states might tend when stable. A key example exhibiting a limit cycle is given by the system

\[\begin{aligned}
&x^{\prime}=\mu x-y-x\left(x^{2}+y^{2}\right) \\[4pt]
&y^{\prime}=x+\mu y-y\left(x^{2}+y^{2}\right)
\end{aligned} \label{3.39} \]

It is clear that the origin is a fixed point. The Jacobian matrix is given as

\[\operatorname{Df}(0,0)=\left(\begin{array}{cc}
\mu & -1 \\[4pt]
1 & \mu
\end{array}\right) \label{3.40} \]

The eigenvalues are found to be \(\lambda=\mu \pm i\). For \(\mu=0\) we have a center For \(\mu<0\) we have a stable spiral and for \(\mu>0\) we have an unstable spiral. However, this spiral does not wander off to infinity. We see in Figure 3.18 that equilibrium point is a spiral. However, in Figure 3.19 it is clear that the solution does not spiral out to infinity. It is bounded by a circle.

Figure 3.18. Phase plane for system (3.39) with \(\mu = 0.4\).

Figure 3.19. Phase plane for system (3.39) with \(\mu = 0.4\) showing that the inner spiral is bounded by a limit cycle.

One can actually find the radius of this circle. This requires rewriting the system in polar form. Recall from Chapter 2 that this is done using

\[r r^{\prime}=x x^{\prime}+y y^{\prime}, \label{3.41} \]

\[r^{2} \theta^{\prime}=x y^{\prime}-y x^{\prime}. \label{3.42} \]

Inserting the system (3.39) into these expressions, we have

\[r r^{\prime}=\mu r^{2}-r^{4}, \quad r^{2} \theta^{\prime}=r^{2}, \nonumber \]

or

\[r^{\prime}=\mu r-r^{3}, \theta^{\prime}=1. \label{3.43} \]

Of course, for a circle \(r=\) const, therefore we need to look at the equilibrium solutions of Equation (3.43). This amounts to solving \(\mu r-r^{3}=0\) for \(r\). The solutions of this equation are \(r=0, \pm \sqrt{\mu}\). We need only keep the one positive radius solution, \(r=\sqrt{\mu}\). In Figures 3.18-3.19 \(\mu=0.4\), so we expect a circle with \(r=\sqrt{0.4} \approx 0.63\). The \(\theta\) equation just tells us that we follow the limit cycle in a counterclockwise direction.

Limit cycles are not always circles. In Figures 3.20-3.21 we show the behavior of the Rayleigh system (3.38) for \(c=0.4\) and \(c=2.0\). In this case we see that solutions tend towards a noncircular limit cycle.

A slight change of the Rayleigh system leads to the van der Pol equation:

\[x^{\prime \prime}+c\left(x^{2}-1\right) x^{\prime}+x=0 \label{3.44} \]

Figure 3.20. Phase plane for the Rayleigh system (3.38) with \(c = 0.4\).

The limit cycle for \(c = 2.0\) is shown in Figure 3.22.

Figure 3.21. Phase plane for the Rayleigh system (3.38) with \(c = 2.0\).

Figure 3.22. Phase plane for the Rayleigh system (3.44) with \(c = 0.4\).

Can one determine ahead of time if a given nonlinear system will have a limit cycle? In order to answer this question, we will introduce some definitions.

Figure 3.23. A sketch depicting the idea of trajectory, or orbit, passing through x.

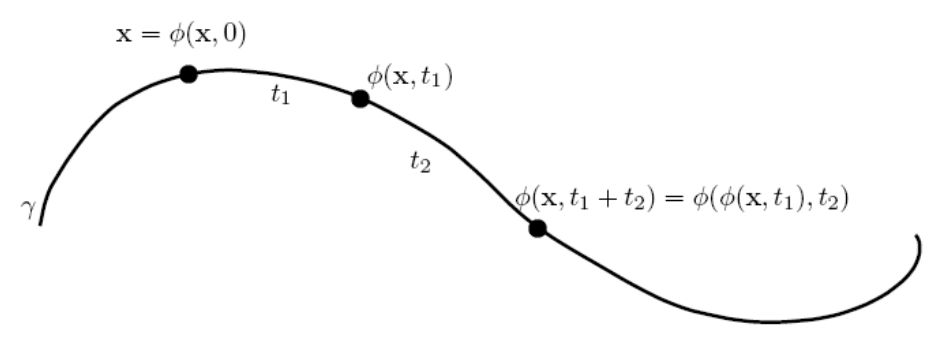
We first describe different trajectories and families of trajectories. A flow on \(R^2\) is a function \(\phi\) that satisfies the following

1. \(\phi(x,t)\) is continuous in both arguments.
2. \(\phi(x,0) = x\) for all \(x \in R^2\).
3. \(\phi(\phi(x,t_1),t_2) = \phi(x, t_1 + t_2)\).

The orbit, or trajectory, through x is defined as \(\gamma = {\phi(x,t)|t \in I}\). In Figure 3.23 we demonstrate these properties. For \(t=0, \phi(x,0) = x\). Increasing \(t\), one follows the trajectory until one reaches the point \(\phi\left(\mathbf{x}, t_{1}\right)\). Continuing \(t_{2}\) further, one is then at \(\phi\left(\phi\left(\mathbf{x}, t_{1}\right), t_{2}\right)\). By the third property, this is the same as going from \(\mathbf{x}\) to \(\phi\left(\mathbf{x}, t_{1}+t_{2}\right)\) for \(t=t_{1}+t_{2}\).

Having defined the orbits, we need to define the asymptotic behavior of the orbit for both positive and negative large times. We define the positive semiorbit through \(\mathbf{x}\) as \(\gamma^{+}=\{\phi(\mathbf{x}, t) \mid t>0\}\). The negative semiorbit through \(\mathbf{x}\) is defined as \(\gamma^{-}=\{\phi(\mathbf{x}, t) \mid t<0\}\). Thus, we have \(\gamma=\gamma^{+} \cup \gamma^{-}\).

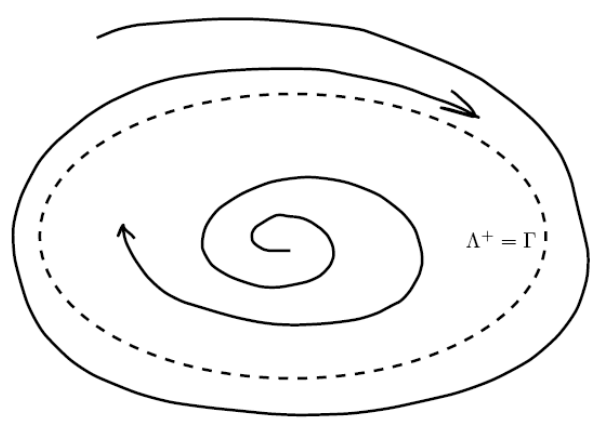
The positive limit set, or \(\omega\)-limit set, of point \(\mathbf{x}\) is defined as

\[\Lambda^{+}=\left\{\mathbf{y} \mid \text { there exists a sequence of } t_{n} \rightarrow \infty \text { such that } \phi\left(\mathbf{x}, t_{n}\right) \rightarrow \mathbf{y}\right\} . \nonumber \]

The \(\mathbf{y}\) 's are referred to as \(\omega\)-limit points. This is shown in Figure 3.24.

Figure 3.24. A sketch depicting an \(\omega\)-limit set. Note that the orbits tends towards the set as \(t\) increases.

Figure 3.25. A sketch depicting an \(\alpha\)-limit set. Note that the orbits tends away from the set as \(t\) increases.

Similarly, we define the negative limit set, or it alpha-limit sets, of point \(\mathbf{x}\) is defined as

\[\Lambda^{-}=\left\{\mathbf{y} \mid\right.$ there exists a sequences of $t_{n} \rightarrow-\infty \text{ such that } \left.\phi\left(\mathbf{x}, t_{n}\right) \rightarrow \mathbf{y}\right\} \nonumber \]

and the corresponding y's are \(\alpha\)-limit points. This is shown in Figure 3.25.
There are several types of orbits that a system might possess. A cycle or periodic orbit is any closed orbit which is not an equilibrium point. A periodic orbit is stable if for every neighborhood of the orbit such that all nearby orbits stay inside the neighborhood. Otherwise, it is unstable. The orbit is asymptotically stable if all nearby orbits converge to the periodic orbit.

A limit cycle is a cycle which is the \(\alpha\) or \(\omega\)-limit set of some trajectory other than the limit cycle. A limit cycle \(\Gamma\) is stable if \(\Lambda^{+}=\Gamma\) for all \(\mathbf{x}\) in some neighborhood of \(\Gamma\). A limit cycle \(\Gamma\) is unstable if \(\Lambda^{-}=\Gamma\) for all \(\mathbf{x}\) in some neighborhood of \(\Gamma\). Finally, a limits cycle is semistable if it is attracting on one side and repelling on the other side. In the previous examples, we saw limit cycles that were stable. Figures 3.24 and 3.25 depict stable and unstable limit cycles, respectively.

We now state a theorem which describes the type of orbits we might find in our system.

Theorem 3.7. Poincaré-Bendixon Theorem

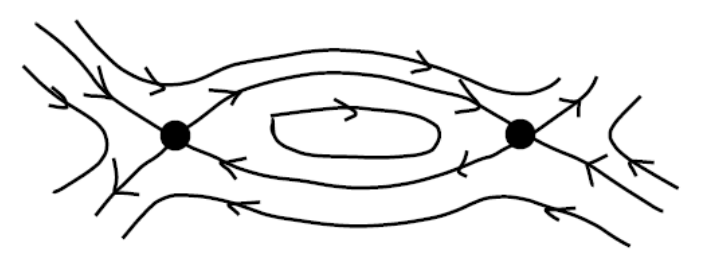
Let \(\gamma^{+}\) be contained in a bounded region in which there are finitely many critical points. Then \(\Lambda^{+}\) is either

1. a single critical point;
2. a single closed orbit;
3. a set of critical points joined by heteroclinic orbits [Compare Figures 3.27 and ??.]

Figure 3.26. A heteroclinic orbit connecting two critical points.

We are interested in determining when limit cycles may, or may not, exist. A consequence of the Poincaré-Bendixon Theorem is given by the following corollary.

Corollary Let \(D\) be a bounded closed set containing no critical points and suppose that \(\gamma^{+} \subset D\). Then there exists a limit cycle contained in \(D\).
More specific criteria allow us to determine if there is a limit cycle in a given region. These are given by Dulac's Criteria and Bendixon's Criteria.

Figure 3.27. A homoclinic orbit returning to the point it left.

Dulac's Criteria

Consider the autonomous planar system

\[x' = f(x,y), \quad y' = g(x,y) \nonumber \]

and a continuously differentiable function \(\psi\) defined on an annular region \(D\) contained in some open set. If

\[\dfrac{\partial}{\partial x}(\psi f) + \dfrac{\partial}{\partial y} (\psi g) \nonumber \]

does not change sign in \(D\), then there is at most one limit cycle contained entirely in \(D\).

Bendixon's Criteria

Consider the autonomous planar system

\[x' = f(x,y), \quad y' = g(x,y) \nonumber \]

defined on a simply connected domain \(D\) such that

\[\dfrac{\partial}{\partial x}(\psi f) + \dfrac{\partial}{\partial y}(\psi g) \neq 0 \nonumber \]

in \(D\). Then there are no limit cycles entirely in \(D\).

These are easily proved using Green's Theorem in the plane. We prove Bendixon's Criteria. Let \(\mathbf{f}=(f, g)\). Assume that \(\Gamma\) is a closed orbit lying in \(D\). Let \(S\) be the interior of \(\Gamma\). Then

\[\begin{aligned}
\int_{S} \nabla \cdot \mathbf{f} d x d y &=\oint_{\Gamma}(f d y-g d x) \\[4pt]
&=\int_{0}^{T}(f \dot{y}-g \dot{x}) d t \\[4pt]
&=\int_{0}^{T}(f g-g f) d t=0
\end{aligned} \label{3.45} \]

So, if \(\nabla \cdot \mathbf{f}\) is not identically zero and does not change sign in \(S\), then from the continuity of \(\nabla \cdot \mathbf{f}\) in \(S\) we have that the right side above is either positive or negative. Thus, we have a contradiction and there is no closed orbit lying in \(D\).

Example 3.8.

Consider the earlier example in (3.39) with \(\mu=1\).

\[\begin{aligned}
x^{\prime} &=x-y-x\left(x^{2}+y^{2}\right) \\[4pt]
y^{\prime} &=x+y-y\left(x^{2}+y^{2}\right) .
\end{aligned} \label{3.46} \]

We already know that a limit cycle exists at \(x^{2}+y^{2}=1\). A simple computation gives that

\[\nabla \cdot \mathbf{f}=2-4 x^{2}-4 y^{2}. \nonumber \]

For an arbitrary annulus \(a<x^{2}+y^{2}<b\), we have

\[2-4 b<\nabla \cdot \mathbf{f}<2-4 a. \nonumber \]

For \(a=3 / 4\) and \(b=5 / 4,-3<\nabla \cdot \mathbf{f}<-1\). Thus, \(\nabla \cdot \mathbf{f}<0\) in the annulus \(3 / 4<x^{2}+y^{2}<5 / 4\). Therefore, by Dulac's Criteria there is at most one limit cycle in this annulus.

Example 3.9.

Consider the system

\[\begin{aligned}
&x^{\prime}=y \\[4pt]
&y^{\prime}=-a x-b y+c x^{2}+d y^{2}
\end{aligned} \label{3.47} \]

Let \(\psi(x, y)=e^{-2 d x}\). Then,

\[\dfrac{\partial}{\partial x}(\psi y)+\dfrac{\partial}{\partial y}\left(\psi\left(-a x-b y+c x^{2}+d y^{2}\right)\right)=-b e^{-2 d x} \neq 0 \nonumber \]

We conclude by Bendixon's Criteria that there are no limit cycles for this system.