1.4: Rotation Matrices and Orthogonal Matrices
- Page ID
- 96140
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)View Rotation Matrix on YouTube
View Orthogonal Matrices on YouTube
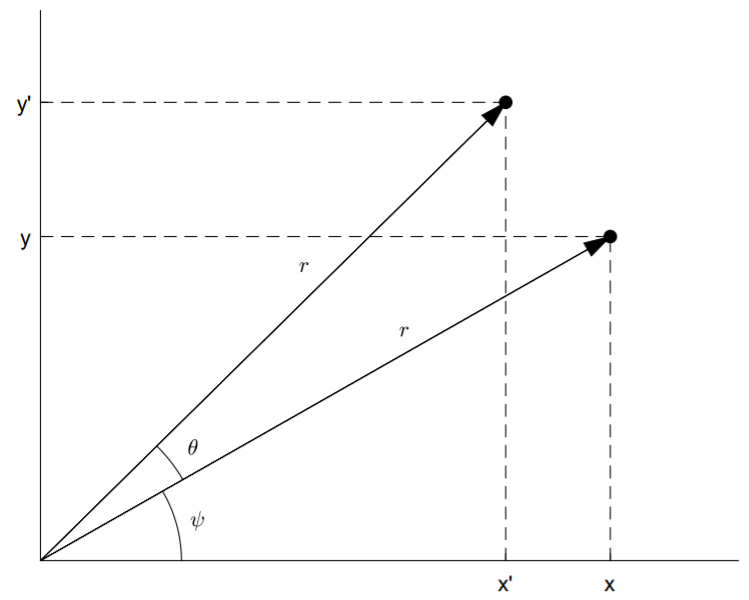
Consider the two-by-two rotation matrix that rotates a vector through an angle \(θ\) in the \(x\)-\(y\) plane, shown above. Trigonometry and the addition formula for cosine and sine results in
\[\begin{aligned} x'&=r\cos(\theta+\psi) \\ &=r(\cos\theta\cos\psi -\sin\theta\sin\psi )\\&=x\cos\theta-y\sin\theta \\ y'&=r\sin(\theta+\psi)\\&=r(\sin\theta\cos\psi+\cos\theta\sin\psi) \\ &=x\sin\theta+y\cos\theta.\end{aligned} \nonumber \]
Writing the equations for \(x'\) and \(y'\) in matrix form, we have
\[\left(\begin{array}{c}x'\\y'\end{array}\right)=\left(\begin{array}{rr}\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right).\nonumber \]
The above two-by-two matrix is called a rotation matrix and is given by
\[\text{R}_\theta =\left(\begin{array}{rr}\cos\theta&-\sin\theta \\ \sin\theta&\cos\theta\end{array}\right).\nonumber \]
Find the inverse of the rotation matrix \(\text{R}_\theta\).
Solution
The inverse of \(\text{R}_θ\) rotates a vector clockwise by \(θ\). To find \(\text{R}^{−1}_θ\), we need only change \(θ → −θ\):
\[\text{R}_\theta^{-1}=\text{R}_{-\theta}=\left(\begin{array}{rr}\cos\theta&\sin\theta \\ -\sin\theta&\cos\theta\end{array}\right).\nonumber \]
This result agrees with (1.4.4) since \(\det\text{ R}_\theta =1\).
Notice that \(\text{R}^{−1}_θ = \text{R}^{\text{T}}_θ\). In general, a square \(n\)-by-\(n\) matrix \(\text{Q}\) with real entries that satisfies
\[\text{Q}^{-1}=\text{Q}^{\text{T}}\nonumber \]
is called an orthogonal matrix. Since \(\text{QQ}^{\text{T}} = \text{I}\) and \(\text{Q}^{\text{T}}\text{Q} = \text{I}\), and since \(\text{QQ}^{\text{T}}\) multiplies the rows of \(\text{Q}\) against themselves, and \(\text{Q}^{\text{T}}\text{Q}\) multiplies the columns of \(\text{Q}\) against themselves, both the rows of \(\text{Q}\) and the columns of \(\text{Q}\) must form an orthonormal set of vectors (normalized and mutually orthogonal). For example, the column vectors of \(\text{R}\), given by
\[\left(\begin{array}{c}\cos\theta \\ \sin\theta\end{array}\right),\quad\left(\begin{array}{r}-\sin\theta \\ \cos\theta\end{array}\right),\nonumber \]
are orthonormal.
It is clear that rotating a vector around the origin doesn’t change its length. More generally, orthogonal matrices preserve inner products. To prove, let \(\text{Q}\) be an orthogonal matrix and \(x\) a column vector. Then
\[(\text{Qx})^{\text{T}}(\text{Qx})=\text{x}^{\text{T}}\text{Q}^{\text{T}}\text{Qx}=\text{x}^{\text{T}}\text{x}.\nonumber \]
The complex matrix analogue of an orthogonal matrix is a unitary matrix \(\text{U}\). Here, the relationship is
\[\text{U}^{-1}=\text{U}^\dagger .\nonumber \]
Like Hermitian matrices, unitary matrices also play a fundamental role in quantum physics.


