2.3.1: Initial Value Problem of Cauchy
( \newcommand{\kernel}{\mathrm{null}\,}\)
Let
x=x0(s), y=y0(s), z=z0(s), p=p0(s), q=q0(s), s1<s<s2,
be a given initial strip such that the strip condition
z′0(s)=p0(s)x′0(s)+q0(s)y′0(s)
is satisfied. Moreover, we assume that the initial strip satisfies the nonlinear equation, that is,
F(x0(s),y0(s),z0(s),p0(s),q0(s))=0.
Initial value problem of Cauchy: Find a C2-solution z=u(x,y) of F(x,y,z,p,q)=0 such that the surface S defined by z=u(x,y) contains the above initial strip.
Similar to the quasilinear case we will show that the set of strips defined by the characteristic system which are fixed onto the initial strip, see Figure 2.3.1.1, fit together and define the surface for which we are looking at.
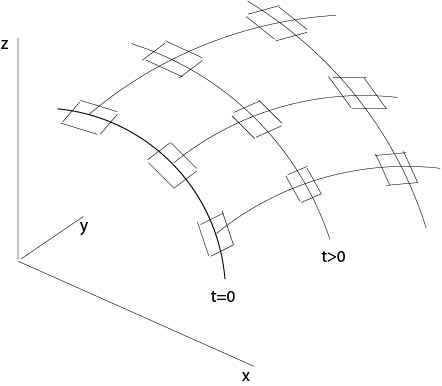
Figure 2.3.1.1: Construction of the solution
Definition. A strip (x(τ),y(τ),z(τ),p(τ),q(τ)), τ1<τ<τ2, is said to be non-characteristic if
$$x'(\tau)F_q(x(\tau),y(\tau),z(\tau),p(\tau),q(\tau))-y'(\tau)F_p(x(\tau),y(\tau),z(\tau),p(\tau),q(\tau))\not=0.\]
Theorem 2.2. For a given non-characteristic initial strip (2.3.1.1), x0, y0, z0∈C2 and p0, q0∈C1 which satisfies the strip condition (2.3.1.2) and the differential equation (2.3.1.3) there exists exactly one solution z=u(x,y) of the Cauchy initial value problem in a neighborhood of the initial curve (x0(s),y0(s),z0(s)), i. e., z=u(x,y) is the solution of the differential equation (2.3.1) and
u(x0(s),y0(s))=z0(s)ux(x0(s),y0(s))=p0(s)uy(x0(s),y0(s))=q0(s).
Proof. Consider the system (2.7)--(2.11) with initial data
x(s,0)=x0(s), y(s,0)=y0(s), z(s,0)=z0(s)p(s,0)=p0(s), q(s,0)=q0(s).
We will show that the surface defined by x=x(s,t), y(s,t) is the surface defined by z=u(x,y), where u is the solution of the Cauchy initial value problem. It turns out that u(x,y)=z(s(x,y),t(x,y)), where s=s(x,y), t=t(x,y) is the inverse of x=x(s,t), y=y(s,t) in a neighborhood of t=0. This inverse exists since the initial strip is non-characteristic by assumption:
$$\det\frac{\partial(x,y)}{\partial(s,t)}\Big|_{t=0}=x_0F_q -y_0F_q\not=0.\]
Set
$$P(x,y)=p(s(x,y),t(x,y)),\ \ Q(x,y)=q(s(x,y),t(x,y)).\]
From Proposition 2.3 and Proposition 2.4 it follows F(x,y,u,P,Q)=0. We will show that P(x,y)=ux(x,y) and Q(x,y)=uy(x,y). To see this, we consider the function
$$h(s,t)=z_s-px_s-qy_s.\]
One has
$$h(s,0)=z_0'(s)-p_0(s)x_0'(s)-q_0(s)y_0'(s)=0\]
since the initial strip satisfies the strip condition by assumption. In the following we will find that for fixed s the function h satisfies a linear homogeneous ordinary differential equation of first order. Consequently, h(s,t)=0 in a neighborhood of t=0. Thus the strip condition is also satisfied along transversal strips to the characteristic strips, see Figure 2.3.1.1.
Then the set of ''scales'' fit together and define a surface like the scales of a fish.
From the definition of h(s,t) and the characteristic equations we get
ht(s,t)=zst−ptxs−qtys−pxst−qyst=∂∂s(zt−pxt−qyt)+psxt+qsyt−qtys−ptxs=(pxs+qys)Fz+Fxxs+Fyzs+Fpps+Fqqs.
Since F(x(s,t),y(s,t),z(s,t),p(s,t),q(s,t))=0, it follows after differentiation of this equation with respect to s the differential equation
$$h_t=-F_zh.\]
Hence h(s,t)≡0, since h(s,0)=0.
Thus we have
zs=pxs+qyszt=pxt+qytzs=uxxs+uyyszt=uxyt+uyyt.
The first equation was shown above, the second is a characteristic equation and the last two follow from z(s,t)=u(x(s,t),y(s,t)). This system implies
(P−ux)xs+(Q−uy)ys=0(P−ux)xt+(Q−uy)yt=0.
It follows P=ux and Q=uy.
The initial conditions
u(x(s,0),y(s,0))=z0(s)ux(x(s,0),y(s,0))=p0(s)uy(x(s,0),y(s,0))=q0(s)
are satisfied since
u(x(s,t),y(s,t))=z(s(x,y),t(x,y))=z(s,t)ux(x(s,t),y(s,t))=p(s(x,y),t(x,y))=p(s,t)uy(x(s,t),y(s,t))=q(s(x,y),t(x,y))=q(s,t).
The uniqueness follows as in the proof of Theorem 2.1.
◻
Example 2.3.1.1:
A differential equation which occurs in the geometrical optic is
$$u_x^2+u_y^2=f(x,y),\]
where the positive function f(x,y) is the index of refraction. The level sets defined by u(x,y)=const. are called {\it wave fronts}. The characteristic curves (x(t),y(t)) are the rays of light. If n is a constant, then the rays of light are straight lines. In R3 the equation is
$$u_x^2+u_y^2+u_z^2=f(x,y,z).\]
Thus we have to extend the previous theory from R2 to Rn, n≥3.
Contributors and Attributions
Integrated by Justin Marshall.


