5.4: Gamma Function

A function that often occurs in the study of special functions is the Gamma function. We will need the Gamma function in the next section on Fourier-Bessel series.

Note

The name and symbol for the Gamma function were first given by Legendre in 1811. However, the search for a generalization of the factorial extends back to the 1720’s when Euler provided the first representation of the factorial as an infinite product, later to be modified by others like Gauß, Weierstraß, and Legendre.

For $x>$ we define the Gamma function as

$$\Gamma(x)=\int_{0}^{\infty} t^{x-1} e^{-t} d t, \quad x>0 .\label{eq:1}$$

The Gamma function is a generalization of the factorial function and a plot is shown in Figure $\PageIndex{1}$. In fact, we have

$$\Gamma(1)=1\nonumber$$

and

$$\Gamma(x+1)=x \Gamma(x) .\nonumber$$

The reader can prove this identity by simply performing an integration by parts. (See Problem 5.7.7.) In particular, for integers $n \in \mathrm{Z}^{+}$, we then have

$$\Gamma(n+1)=n \Gamma(n)=n(n-1) \Gamma(n-2)=n(n-1) \cdots 2 \Gamma(1)=n ! .\nonumber$$

Figure $\PageIndex{1}$: Plot of the Gamma function.

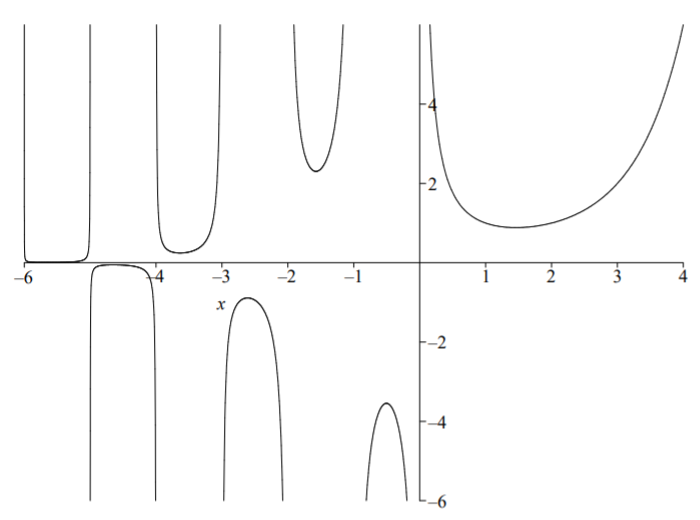
We can also define the Gamma function for negative, non-integer values of $x$. We first note that by iteration on $n \in \mathrm{Z}^{+}$, we have

$$\Gamma(x+n)=(x+n-1) \cdots(x+1) x \Gamma(x), \quad x+n>0 .\nonumber$$

Solving for $\Gamma(x)$, we then find

$$\Gamma(x)=\frac{\Gamma(x+n)}{(x+n-1) \cdots(x+1) x^{\prime}}, \quad-n<x<0\nonumber$$

Note that the Gamma function is undefined at zero and the negative integers.

Example $\PageIndex{1}$

We now prove that

$$\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi} \text {. }\nonumber$$

Solution

This is done by direct computation of the integral:

$$\Gamma\left(\frac{1}{2}\right)=\int_{0}^{\infty} t^{-\frac{1}{2}} e^{-t} d t .\nonumber$$

Letting $t=z^{2}$, we have

$$\Gamma\left(\frac{1}{2}\right)=2 \int_{0}^{\infty} e^{-z^{2}} d z .\nonumber$$

Due to the symmetry of the integrand, we obtain the classic integral

$$\Gamma\left(\frac{1}{2}\right)=\int_{-\infty}^{\infty} e^{-z^{2}} d z,\nonumber$$

which can be performed using a standard trick.$^{1}$ Consider the integral

$$I=\int_{-\infty}^\infty e^{-x^2}dx.\nonumber$$

Then,

$$I^{2}=\int_{-\infty}^{\infty} e^{-x^{2}} d x \int_{-\infty}^{\infty} e^{-y^{2}} d y .\nonumber$$

Note that we changed the integration variable. This will allow us to write this product of integrals as a double integral:

$$I^{2}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-\left(x^{2}+y^{2}\right)} d x d y .\nonumber$$

This is an integral over the entire $xy$-plane. We can transform this Cartesian integration to an integration over polar coordinates. The integral becomes

$$I^{2}=\int_{0}^{2 \pi} \int_{0}^{\infty} e^{-r^{2}} r d r d \theta\nonumber$$

This is simple to integrate and we have $I^{2}=\pi$. So, the final result is found by taking the square root of both sides.

$$\Gamma\left(\frac{1}{2}\right)=I=\sqrt{\pi} .\nonumber$$

Note

In Example 9.5 we show the more general result:

$$\int_{-\infty}^{\infty} e^{-\beta y^{2}} d y=\sqrt{\frac{\pi}{\beta}}\nonumber$$

In Problem 5.7.12 the reader will prove the identity

$$\Gamma\left(n+\frac{1}{2}\right)=\frac{(2 n-1) ! !}{2^{n}} \sqrt{\pi} .\nonumber$$

Another useful relation, which we only state, is

$$\Gamma(x) \Gamma(1-x)=\frac{\pi}{\sin \pi x} .\nonumber$$

The are many other important relations, including infinite products, which we will not need at this point. The reader is encouraged to read about these elsewhere. In the meantime, we move on to the discussion of another important special function in physics and mathematics.