5.3: Theorems of Hyperbolic Geometry
- Page ID
- 89859
Note when working on these problems the model may be useful in figuring out why something works. However the proofs should be directly based on the axioms. It is legitimate to prove a statement using the model description if the model has been proven to be equivalent to the axioms. For this course proofs using the model will be worth fewer points than proofs directly from the axioms.
Given a line and a point not on that line there exists infinitely many lines through that point parallel to the given line.
Given a line and a point not on that line there exists a first line through that point parallel to the given line.
A line is a sensed parallel if and only if it is the first line parallel to a given line on that side through a given point.
The smaller angle formed by a sensed parallel and a transversal through the given point is the angle of parallelism if and only if the transversal is perpendicular to the given line.
The angle of parallelism is the same on the left and right.
The angle of parallelism is less than π/2.
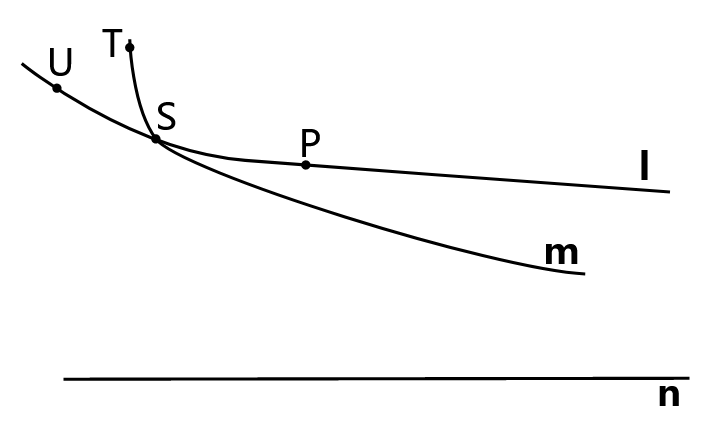
Consider the following illustrated in \(\PageIndex{1}\). ℓ is the right sensed parallel to n at P. Let S be on ℓ to the left of P. Suppose line m through S is the sensed parallel to n at S. Show that if T is on m to the left of S then must be below TP to the right of T. Further if U on ℓ such that U-S-P and A=TP∩n, then sensed parallel must be above SA to the right of A and above UA.
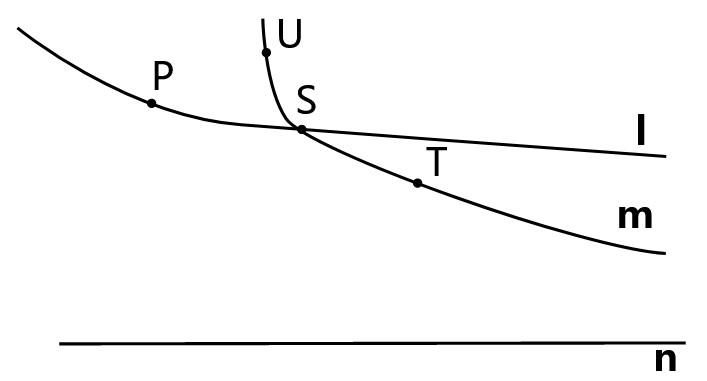
Consider the following illustrated in \(\PageIndex{2}\). ℓ is the right sensed parallel to n at P. Let S be on ℓ to the right of P. Suppose line m through S is the sensed parallel to n at S. Show that if U and T are on such that U-S-T and A=TP∩n then m is below UA to the right of U and above PA.
If ℓ is the right sensed parallel to m at P, then ℓ is the right sensed parallel to m at any point to the left of P on ℓ.
If ℓ is the sensed parallel to m at a point P, then ℓ is the sensed parallel to m at any point Q also on ℓ.
A pair of parallel lines and a transversal is a omega triangle if and only if the parallels are sensed parallels.
Draw an omega triangle using the Poincaré disc model.
If a line k contains a vertex and an interior point of an omega triangle, it intersects the side opposite the vertex.
Does a version of Pasch's Axiom work for omega triangles? Let ℓ and m be sensed parallels. Let AB be a transversal with A∈ℓ and B∈m Let M be the midpoint of AB and D be the foot of the perpendicular from M to ℓ. Also choose F∈m on the opposite side of AB from D such that BF≌AD Let C∈ℓ be such that C-A-D. Prove that ∠CAB≢∠ABω.
An exterior angle of an omega triangle is greater than the opposite interior angle.
Two omega triangles are congruent if the length of the finite sides and the measure of one pair of corresponding angles are congruent.
Two omega triangles are congruent if corresponding pairs of angles are congruent.