12.3: Auxiliary statements
- Page ID
- 23656
One may compare the conformal model with a telescope — it makes it possible to see the h-plane from the Euclidean plane. Continuing this analogy further, we may say that the following lemma will be used to aim the telescope at any particular point in the h-plane.
Consider an h-plane with a unit circle as the absolute. Let \(O\) be the center of the absolute and \(P\) be another h-point. Suppose that \(P'\) denotes the inverse of \(P\) in the absolute.
Then the circle \(\Gamma\) with the center \(P'\) and radius \(\dfrac{\sqrt{1-OP^2}}{OP}\) is perpendicular to the absolute. Moreover, \(O\) is the inverse of \(P\) in \(\Gamma\).
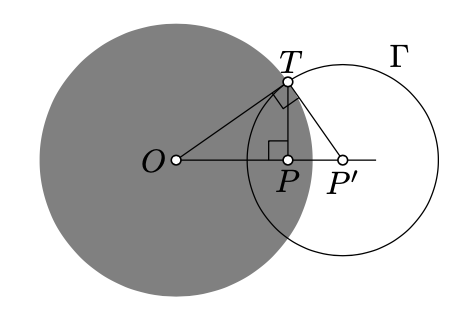
- Proof
-
Follows from Exercise 10.5.2.
Assume \(\Gamma\) is a circline that is perpendicular to the absolute. Consider the inversion \(X \mapsto X'\) in \(\Gamma\), or if \(\Gamma\) is a line, set \(X \mapsto X'\) to be the reflection across \(\Gamma\).
The following observation says that the map \(X \mapsto X'\) respects all the notions introduced in the previous section. Together with the lemma above, it implies that in any problem that is formulated entirely in h-terms we can assume that a given h-point lies in the center of the absolute.
The map \(X \mapsto X'\) described above is a bijection from the h-plane to itself. Moreover, for any h-points \(P\), \(Q\), \(R\) such that \(P\ne Q\) and \(Q\ne R\), the following conditions hold:
- The h-line \((PQ)_h\), h-half-line \([PQ)_h\), and h-segment \([PQ]_h\) are transformed into \((P'Q')_h\), \([P'Q')_h\), and \([P'Q']_h\) respectively.
- \(\delta(P',Q')=\delta(P,Q)\) and \(P'Q'_h=PQ_h\).
- \(\measuredangle_h P'Q'R' \equiv -\measuredangle_h PQR\).
It is instructive to compare this observation with Proposition [prop:reflection].
- Proof
-
According to Theorem 10.5.1, the map sends the absolute to itself. Note that the points on \(\Gamma\) do not move, it follows that points inside of the absolute remain inside after the mapping. Whence the \(X \mapsto X'\) is a bijection from the h-plane to itself.
Part (a) follows from Theorem 10.3.1 and Theorem 10.6.1.
Part (b) follows from Theorem 10.2.1.
Part (c) follows from Theorem 10.6.1.
Assume that the absolute is a unit circle centered at \(O\). Given an h-point \(P\), set \(x=OP\) and \(y=OP_h\). Then
\(y = \ln \dfrac{1 + x}{1 - x}\) and \(x = \dfrac{e^y - 1}{e^y + 1}.\)
Observe that according to lemma, \(OP_h \to \infty\) as \(OP \to 1\). That is if \(P\) approaches absolute in Euclidean sense, it escapes to infinity in the h-sense.
- Proof
-
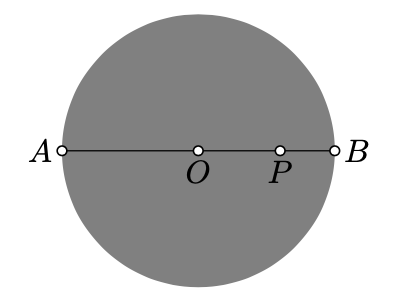
Note that the h-line \((OP)_h\) forms a diameter of the absolute. If \(A\) and \(B\) are the ideal points as in the definition of h-distance, then
\(\begin{array} {l} {OA = OB = 1,} \\ {PA = 1 + x,} \\ {PB = 1 - x.} \end{array}\)
In particular,
\(y = \ln \dfrac{AP \cdot BO}{PB \cdot OA} = \ln \dfrac{1 + x}{1 - x}.\)
Taking the exponential function of the left and the right hand side and applying obvious algebra manipulations, we get that
\(x=\dfrac{e^y-1}{e^y+1}\).
Assume the points \(P\), \(Q\), and \(R\) appear on one h-line in the same order. Then
\(PQ_h + QR_h = PR_h.\)
- Proof
-
Note that
\(PQ_h + QR_h = PR_h\)
is equivalent to
\[\delta (P, Q) \cdot \delta (Q,R) = \delta (P, R).\]
Let \(A\) and \(B\) be the ideal points of \((PQ)_h\). Without loss of generality, we can assume that the points \(A\), \(P\), \(Q\), \(R\), and \(B\) appear in the same order on the circline containing \((PQ)_h\). Then
\(\begin{array} {rcl} {\delta (P, Q) \cdot \delta (Q, R)} & = & {\dfrac{AQ \cdot BP}{QB \cdot PA} \cdot \dfrac{AR \cdot BQ}{RB \cdot QA} =} \\ {} & = & {\dfrac{AR \cdot BP}{RB \cdot PA} =} \\ {} & = & {\delta (P, R).} \end{array}\)
Hence 12.3.1 follows.
Let \(P\) be an h-point and \(\rho>0\). The set of all h-points \(Q\) such that \(PQ_h=\rho\) is called an h-circle with the center \(P\) and the h-radius \(\rho\).
Any h-circle is a Euclidean circle that lies completely in the h-plane.
More precisely for any h-point \(P\) and \(\rho\ge 0\) there is a \(\hat\rho\ge 0\) and a point \(\hat P\) such that
for any h-point \(Q\).
Moreover, if \(O\) is the center of the absolute, then
- \(\hat{O}=O\) for any \(\rho\) and
- \(\hat{P} \in (OP)\) for any \(P\ne O\).
- Proof
-
According to Lemma \(\PageIndex{2}\), \(OQ_h\z= \rho\) if and only if
Therefore, the locus of h-points \(Q\) such that \(OQ_h= \rho\) is a Euclidean circle, denote it by \(\Delta_{\rho}\).
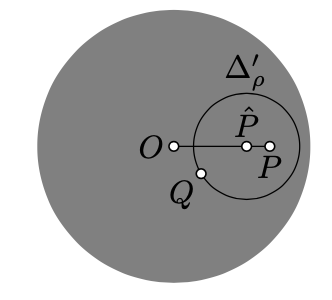
If \(P \ne O\), then by Lemma \(\PageIndex{1}\) and the main observation (Theorem \(\PageIndex{1}\)) there is inversion that respects all h-notions and sends \(O \mapsto P\).
Let \(\Delta_{\rho}'\) be the inverse of \(\Delta_{\rho}\). Since the inversion preserves the h-distance, \(PQ_h=\rho\) if and only if \(Q \in \Delta_{\rho}'\).
According to Theorem 10.3.1, \(\Delta_\rho'\) is a Euclidean circle. Let \(\hat P\) and \(\hat\rho\) denote the Euclidean center and radius of \(\Delta_\rho'\).
Finally, note that \(\Delta_\rho'\) reflects to itself across \((OP)\); that is, the center \(\hat P\) lies on \((OP)\).
Assume \(P\), \(\hat P\), and \(O\) are as in the Lemma \(\PageIndex{1}\) and \(P \ne O\). Show that \(\hat{P} \in [OP]\).
- Hint
-
Let \(X\) and \(Y\) denote the point of intersections of \((OP)\) and \(\Delta_{rho}'\). Consider an isometry \((OP) \to \mathbb{R}\) such that \(O\) corresponds to 0. Let \(x, y, p\), and \(\hat{p}\) denote the real number corresponding to \(X, Y, P\), and \(\hat{P}\).
We can assume that \(p > 0\) and \(x < y\). Note that \(\hat{p} = \dfrac{x + y}{2}\) and
\(\dfrac{(1 + x) \cdot (1 - p)}{(1 - x) \cdot (1 + p)} = \dfrac{(1 + p) \dot (1 - y)}{(1 - p) \cdot (1 + y)}\).
It remains to show that all this implies \(0 < \hat{p} < p\).


