13.3: Circles, Horocycles, and Equidistants
- Page ID
- 23663
Note that according to Lemma 12.3.4, any h-circle is a Euclidean circle that lies completely in the h-plane. Further, any h-line is an intersection of the h-plane with the circle perpendicular to the absolute. In this section we will describe the h-geometric meaning of the intersections of the other circles with the h-plane.
You will see that all these intersections have a perfectly round shape in the h-plane. One may think of these curves as trajectories of a car with a fixed position of the steering wheel. In the Euclidean plane, this way you either run along a circle or along a line. In the hyperbolic plane, the picture is different. If you turn the steering wheel to the far right, you will run along a circle. If you turn it less, at a certain position of the wheel, you will never come back to the same point, but the path will be different from the line. If you turn the wheel further a bit, you start to run along a path that stays at some fixed distance from an h-line.
Equidistants of h-lines. Consider the h-plane with the absolute \(\Omega\). Assume a circle \(\Gamma\) intersects \(\Omega\) in two distinct points, \(A\) and \(B\). Suppose that \(g\) denotes the intersection of \(\Gamma\) with the h-plane.
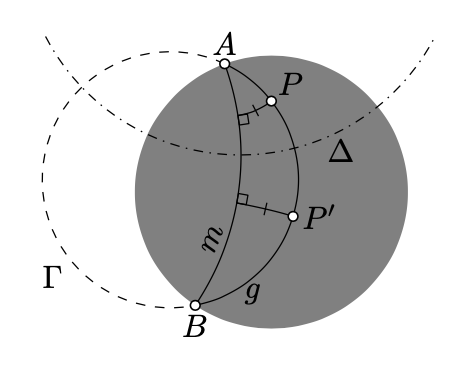
Let us draw an h-line \(m\) with the ideal points \(A\) and \(B\). According to Exercise 12.1.1, \(m\) is uniquely defined.
Consider any h-line \(\ell\) perpendicular to \(m\); let \(\Delta\) be the circle containing \(\ell\).
Note that \(\Delta\perp \Gamma\). Indeed, according to Corollary 10.5.1, \(m\) and \(\Omega\) invert to themselves in \(\Delta\). It follows that \(A\) is the inverse of \(B\) in \(\Delta\). Finally, by Corollary 10.5.2, we get that \(\Delta\perp \Gamma\).
Therefore, inversion in \(\Delta\) sends both \(m\) and \(g\) to themselves. For any two points \(P',P\in g\) there is a choice of \(\ell\) and \(\Delta\) as above such that \(P'\) is the inverse of \(P\) in \(\Delta\). By the main observation (Theorem 12.3.1) the inversion in \(\Delta\) is a motion of the h-plane. Therefore, all points of \(g\) lie on the same distance from \(m\).
In other words, \(g\) is the set of points that lie on a fixed h-distance and on the same side of \(m\).
Such a curve \(g\) is called equidistant to h-line \(m\). In Euclidean geometry, the equidistant from a line is a line; apparently in hyperbolic geometry the picture is different.
Horocycles. If the circle \(\Gamma\) touches the absolute from inside at one point \(A\), then the complement \(h=\Gamma\backslash\{A\}\) lies in the h-plane. This set is called a horocycle. It also has a perfectly round shape in the sense described above.
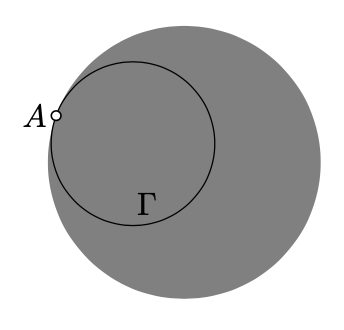
The shape of a horocycle is between shapes of circles and equidistants to h-lines. A horocycle might be considered as a limit of circles thru a fixed point with the centers running to infinity along a line. The same horocycle is a limit of equidistants thru a fixed point to sequence of h-lines that runs to infinity.
Since any three points lie on a circline, we have that any nondegenerate h-triangle is inscribed in an h-circle, horocycle or an equidistant.
Find the leg of an isosceles right h-triangle inscribed in a horocycle.
- Hint
-
As usual, we assume that the absolute is a unit circle.
Let \(PQR\) be a hyperbolic triangle with a right angle at \(Q\), such that \(PQ_h = QR_h\) and the vertices \(P, Q\), and \(R\) lie on a horocycle.
Without loss of generality, we may assume that \(Q\) is the center of the absolute. In this case \(\measuredangle_h PQR = \measuredangle PQR = \pm \dfrac{\pi}{2}\) and \(PQ = QR\).
Note that Euclidean circle passing thru \(P, Q\), and \(R\) is tangent to the absolute. Conclude that \(PQ = \dfrac{1}{\sqrt{2}}\). Apply Lemma 12.3.2 to find \(PQ_h\).


