13.2: Inradius of h-triangle

Last updated
Save as PDF

Page ID: 23662

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Theorem $\PageIndex{1}$

The inradius of any h-triangle is less than $\dfrac{1}{2} \cdot \ln3$.

Proof

Let $I$ and $r$ be the h-incenter and h-inradius of $\triangle_hXYZ$.

Note that the h-angles $XIY$, $YIZ$ and $ZIX$ have the same sign. Without loss of generality, we can assume that all of them are positive and therefore

$\measuredangle_hXIY+ \measuredangle_hYIZ+ \measuredangle_hZIX=2 \cdot \pi$

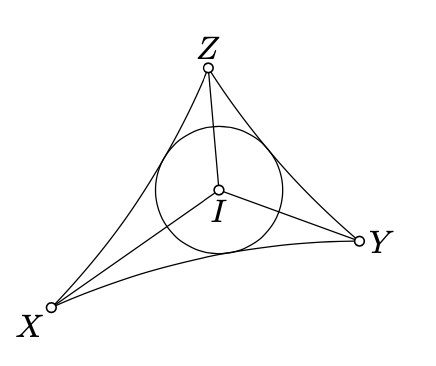
$截屏2021-02-24 下午3.30.51.png$

We can assume that $\measuredangle_hXIY \ge \dfrac{2}{3} \cdot \pi$; if not relabel $X$, $Y$, and $Z$.

Since $r$ is the h-distance from $I$ to $(XY)_h$, Proposition 13.1.1 implies that

$\begin{array} {rcl} {r} & < & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \cos \dfrac{\pi}{3}}{1 - \cos \dfrac{\pi}{3}}} \\ {} & = & {\dfrac{1}{2} \cdot \ln \dfrac{1 + \dfrac{1}{2}}{1 - \dfrac{1}{2}}} \\ {} & = & {\dfrac{1}{2} \cdot \ln 3.} \end{array}$

Exercise $\PageIndex{1}$

Let $\square_h ABCD$ be a quadrangle in the h-plane such that the h-angles at $A$, $B$, and $C$ are right and $AB_h=BC_h$. Find the optimal upper bound for $AB_h$.

Hint

Note that the angle of prarllelism of $B$ to $(CD)_h$ is bigger than $\dfrac{\pi}{4}$, and it converge to $\dfrac{\pi}{4}$ as $CD_h \to \infty$.

Applying Proposition 13.1.1, we get that

$BC_h < \dfrac{1}{2} \cdot \ln \dfrac{1 + \dfrac{1}{\sqrt{2}}}{1 - \dfrac{1}{\sqrt{2}}} = \ln (1 + \sqrt{2}).$

The right hand side is the limit of $BC_h$ if $CD_h \to \infty$. Therefore, $\ln (1 + \sqrt{2})$ is the optimal upper bound.