17.1: Special bijection on the h-plane
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider the conformal disc model with the absolute at the unit circle Ω centered at O. Choose a coordinate system (x,y) on the plane with the origin at O, so the circle Ω is described by the equation x2+y2=1.
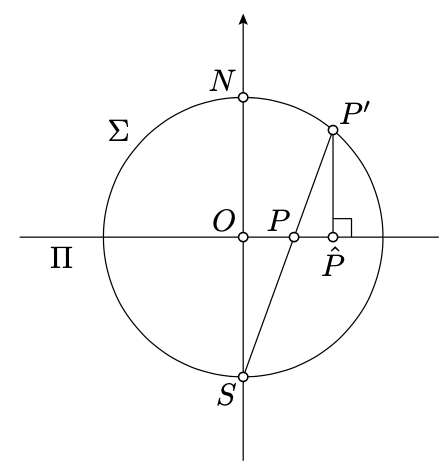
The plane thru P,O, and S.
Let us think that our plane is the coordinate xy-plane in the Euclidean space; denote it by Π. Let Σ be the unit sphere centered at O; it is described by the equation
x2+y2+z2=1.
Set S=(0,0,−1) and N=(0,0,1); these are the south and north poles of Σ.
Consider stereographic projection Π→Σ from S; given point P∈Π denote its image in Σ. Note that the h-plane is mapped to the north hemisphere; that is, to the set of points (x,y,z) in Σ described by the inequality z>0.
For a point P′∈Σ consider its foot point ˆP on Π; this is the closest point to P′.
Note that the composition P↔P′↔ˆP of these two maps gives a bijection from the h-plane to itself. Further note that P=ˆP if and only if P∈Ω or P=O.
Suppose that P↔ˆP is the bijection described above. Assume that P is a point of h-plane distinct from the center of absolute and Q is its inverse in the absolute. Show that the midpoint of [PQ] is the inversion of ˆP in the absolute.
- Hint
-
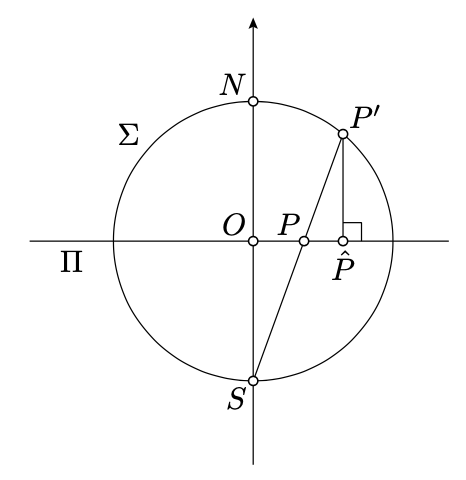
Let N,O,S,P,P′ and ˆP be as on the diagram above.
Note that QQ=1x and therefore we need to show that OˆP=2/(x+1x). To do this, show and use that △SOP∼△SP′N∼△P′ˆPP and 2⋅SO=NS.
Let (PQ)h be an h-line with the ideal points A and B. Then ˆP,ˆQ∈[AB].
Moreover,
AˆQ⋅BˆP^QB⋅ˆPA=(AQ⋅BPQB⋅PA)2.
In particular, if A,P,Q,B appear in the same order, then
PQh=12⋅lnAˆQ⋅BˆPˆQB⋅ˆPA.
- Proof
-
Consider the stereographic projection Π→Σ from the south pole S. Note that it fixes A and B; denote by P′ and Q′ the images of P and Q;
According to Theorem 16.3.1c,
AQ⋅BPQB⋅PA=AQ′⋅BP′Q′B⋅P′A.
By Theorem Theorem 16.3.1e, each circline in Π that is perpendicular to Ω is mapped to a circle in Σ that is still perpendicular to Ω. It follows that the stereographic projection sends (PQ)h to the intersection of the north hemisphere of Σ with a plane perpendicular to Π.
Suppose that Λ denotes the plane; it contains the points A, B, P′, ˆP and the circle Γ=Σ∩Λ. (It also contains Q′ and ˆQ but we will not use these points for a while.)
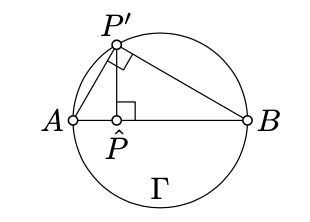
The plane Λ.Note that
- A,B,P′∈Γ,
- [AB] is a diameter of Γ,
- (AB)=Π∩Λ,
- ˆP∈[AB]
- (P′ˆP⊥(AB).
Since [AB] is the diameter of Γ, by Corollary 9.8, the angle AP′B is right. Hence △AˆPP′∼△AP′B∼△P′ˆPB. In particular
AP′BP′=AˆPP′ˆP=P′ˆPBˆP.
Therefore
AˆPBˆP=(AP′BP′)2.
The same way we get that
AˆQBˆQ=(AQ′BQ′)2.
Finally, note that 17.1.2+17.1.3+17.1.4 imply 17.1.1
The last statement follows from 17.1.1 and the definition of h-distance. Indeed,
PQh:=lnAQ⋅BPQB⋅PA==ln(AˆQ⋅BˆPˆQB⋅ˆPA)12==12⋅lnAˆQ⋅BˆPˆQB⋅ˆPA.
Let Γ1, Γ2, and Γ3 be three circles perpendicular to the circle Ω. Let [A1B1], [A2B2], and [A3B3] denote the common chords of Ω and Γ1, Γ2, Γ3 respectively. Show that the chords [A1B1], [A2B2], and [A3B3] intersect at one point inside Ω if and only if Γ1, Γ2, and Γ3 intersect at two points.
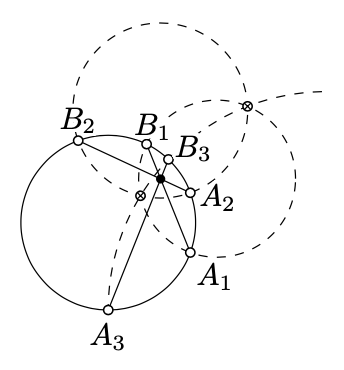
- Hint
-
Consider the bijection P↔ˆP of the h-plane with absolute Ω. Note that ˆP∈[AiBi] if and only if P∈Γi.


