17.1: Special bijection on the h-plane

Last updated
Save as PDF

Page ID: 23689

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Consider the conformal disc model with the absolute at the unit circle $\Omega$ centered at $O$. Choose a coordinate system $(x,y)$ on the plane with the origin at $O$, so the circle $\Omega$ is described by the equation $x^2+y^2=1$.

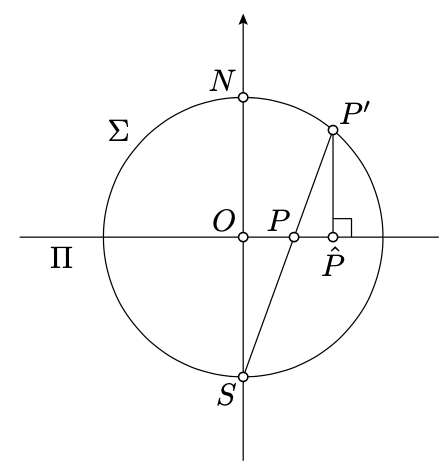
$截屏2021-03-01 上午10.40.49.png$
The plane thru $P, O$, and $S$.

Let us think that our plane is the coordinate $xy$-plane in the Euclidean space; denote it by $\Pi$. Let $\Sigma$ be the unit sphere centered at $O$; it is described by the equation

$x^2+y^2+z^2=1.$

Set $S=(0,0,-1)$ and $N=(0,0,1)$; these are the south and north poles of $\Sigma$.

Consider stereographic projection $\Pi\to\Sigma$ from $S$; given point $P\in\Pi$ denote its image in $\Sigma$. Note that the h-plane is mapped to the north hemisphere; that is, to the set of points $(x,y,z)$ in $\Sigma$ described by the inequality $z>0$.

For a point $P'\in \Sigma$ consider its foot point $\hat P$ on $\Pi$; this is the closest point to $P'$.

Note that the composition $P \leftrightarrow P' \leftrightarrow \hat{P}$ of these two maps gives a bijection from the h-plane to itself. Further note that $P=\hat{P}$ if and only if $P\in \Omega$ or $P=O$.

Exercise $\PageIndex{1}$

Suppose that $P\leftrightarrow \hat P$ is the bijection described above. Assume that $P$ is a point of h-plane distinct from the center of absolute and $Q$ is its inverse in the absolute. Show that the midpoint of $[PQ]$ is the inversion of $\hat{P}$ in the absolute.

Hint

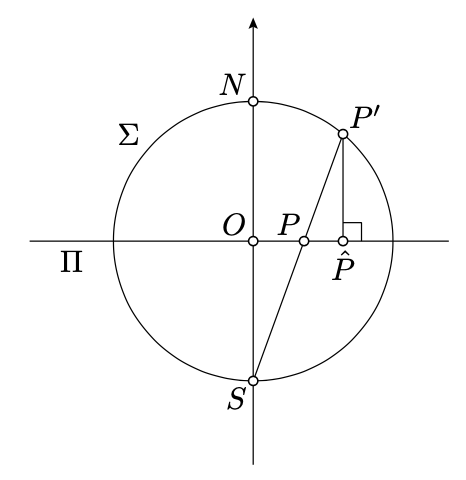
$截屏2021-03-01 上午11.23.55.png$

Let $N, O, S, P, P'$ and $\hat{P}$ be as on the diagram above.

Note that $QQ = \dfrac{1}{x}$ and therefore we need to show that $O\hat{P} = 2/(x + \dfrac{1}{x})$. To do this, show and use that $\triangle SOP \sim \triangle SP'N \sim \triangle P'\hat{P}P$ and $2 \cdot SO = NS$.

Lemma $\PageIndex{1}$

Let $(PQ)_h$ be an h-line with the ideal points $A$ and $B$. Then $\hat P,\hat Q\in[AB]$.

Moreover,

\[\dfrac{A \hat{Q} \cdot B \hat{P}}{\hat{QB}\cdot \hat{P}A} = (\dfrac{AQ\cdot BP}{QB\cdot PA})^2. \]

In particular, if $A,P,Q,B$ appear in the same order, then

$PQ_h=\dfrac{1}{2} \cdot \ln \dfrac{A\hat{Q}\cdot B\hat{P}}{\hat{Q}B\cdot \hat{P}A}.$

Proof

Consider the stereographic projection $\Pi \to \Sigma$ from the south pole $S$. Note that it fixes $A$ and $B$; denote by $P'$ and $Q'$ the images of $P$ and $Q$;

According to Theorem 16.3.1c,

\[\dfrac{AQ\cdot BP}{QB\cdot PA}=\dfrac{AQ'\cdot BP'}{Q'B\cdot P'A}.\]

By Theorem Theorem 16.3.1e, each circline in $\Pi$ that is perpendicular to $\Omega$ is mapped to a circle in $\Sigma$ that is still perpendicular to $\Omega$. It follows that the stereographic projection sends $(PQ)_h$ to the intersection of the north hemisphere of $\Sigma$ with a plane perpendicular to $\Pi$.

Suppose that $\Lambda$ denotes the plane; it contains the points $A$, $B$, $P'$, $\hat P$ and the circle $\Gamma=\Sigma\cap\Lambda$. (It also contains $Q'$ and $\hat{Q}$ but we will not use these points for a while.)

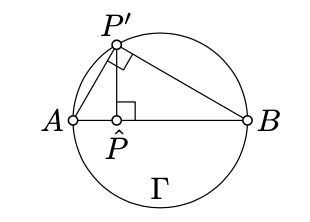
$截屏2021-03-01 上午11.16.24.png$
The plane $\Lambda$.

Note that

$A,B,P'\in\Gamma$,
$[AB]$ is a diameter of $\Gamma$,
$(AB)=\Pi\cap\Lambda$,
$\hat{P} \in [AB]$
$(P'\hat{P} \perp (AB).$

Since $[AB]$ is the diameter of $\Gamma$, by Corollary 9.8, the angle $AP'B$ is right. Hence $\triangle A\hat PP' \sim \triangle AP'B \sim \triangle P'\hat PB$. In particular

$\dfrac{AP'}{BP'}=\dfrac{A \hat{P}}{P'\hat{P}}=\dfrac{P'\hat{P}}{B\hat{P}}.$

Therefore

\[\dfrac{A\hat{P}}{B\hat{P}}=(\dfrac{AP'}{BP'})^2.\]

The same way we get that

\[\dfrac{A\hat{Q}}{B\hat{Q}}=(\dfrac{AQ'}{BQ'})^2.\]

Finally, note that 17.1.2+17.1.3+17.1.4 imply 17.1.1

The last statement follows from 17.1.1 and the definition of h-distance. Indeed,

$\begin{aligned} PQ_h&:=\ln\frac{A Q\cdot B P}{QB\cdot PA}= \\ &=\ln\left(\frac{A \hat Q\cdot B \hat P}{\hat QB\cdot \hat PA}\right)^{\frac12}= \\ &=\tfrac12\cdot\ln\frac{A \hat Q\cdot B \hat P}{\hat QB\cdot \hat PA}.\end{aligned}$

Exercise $\PageIndex{2}$

Let $\Gamma_1$, $\Gamma_2$, and $\Gamma_3$ be three circles perpendicular to the circle $\Omega$. Let $[A_1B_1]$, $[A_2B_2]$, and $[A_3B_3]$ denote the common chords of $\Omega$ and $\Gamma_1$, $\Gamma_2$, $\Gamma_3$ respectively. Show that the chords $[A_1B_1]$, $[A_2B_2]$, and $[A_3B_3]$ intersect at one point inside $\Omega$ if and only if $\Gamma_1$, $\Gamma_2$, and $\Gamma_3$ intersect at two points.

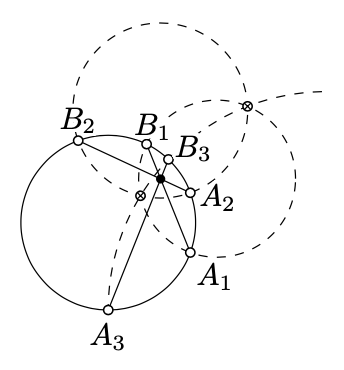
$截屏2021-03-01 上午11.21.52.png$

Hint: Consider the bijection $P \leftrightarrow \hat{P}$ of the h-plane with absolute $\Omega$. Note that $\hat{P} \in [A_iB_i]$ if and only if $P \in \Gamma_i$.

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{1}\)

Lemma \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)