4.5: Special Right Triangles
- Page ID
- 34139
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There are two kinds of right triangle which deserve special attention: the \(30^{\circ}-60^{\circ}-90^{\circ}\) right triangle and the \(45^{\circ}-45^{\circ}-90^{\circ}\) right triangle.
30°−60°−90° Right Triangles
A triangle whose angles are \(30^{\circ}, 60^{\circ},\) and \(90^{\circ}\) is called a \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle. \(\triangle ABC\) in Figure \(\PageIndex{1}\) is a \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle with side \(AC=1\).
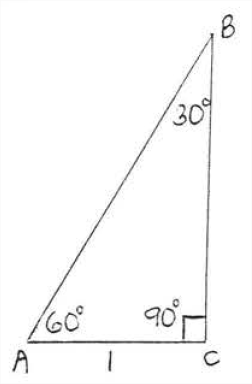
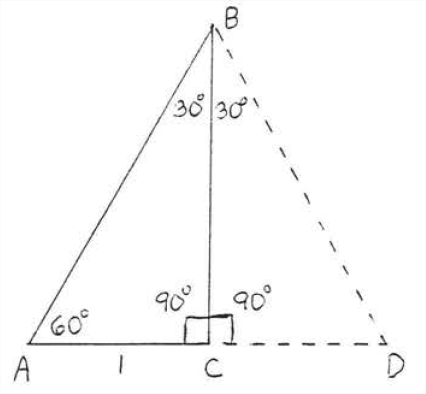
To learn more about this triangle let us draw lines \(BD\) and \(CD\) as in Figure \(\PageIndex{2}\). \(\triangle ABC \cong \triangle DBC\) by \(ASA = ASA\) so \(AC = DC = 1.\) \(\triangle ABD\) is an equiangular triangle so all the sides must be equal to \(2.\). Therefore \(AB=2\) (Figure \(\PageIndex{3}\)).
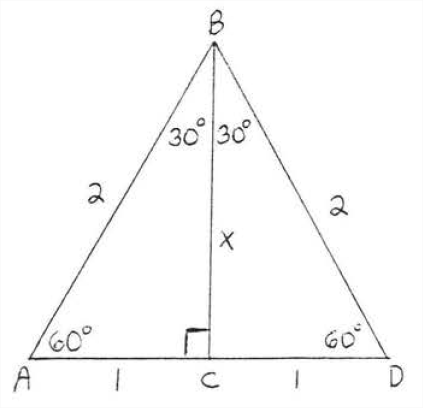
Let \(x = BC\). Let us find \(x\). Applying the Pythagorean Theorem to \(\triangle ABC\),
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {1^2 + x^2} & = & {x^2} \\ {1 + x^2} & = & {4} \\ {x^2} & = & {3} \\ {x} & = & {\sqrt{3}} \end{array}\)
Now suppose we are given another \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle \(\triangle DEF\), with side \(DF = 8\) (Figure \(\PageIndex{4}\)). \(\triangle DEF\) is similar to \(\triangle ABC\) of Figure \(\PageIndex{3}\) Therefore
\(\begin{array} {rcl} {\dfrac{DF}{AC}} & = & {\dfrac{DE}{AB}} \\ {\dfrac{8}{1}} & = & {\dfrac{DE}{2}} \\ {16} & = & {DE} \end{array}\) and \(\begin{array} {rcl} {\dfrac{DF}{AC}} & = & {\dfrac{EF}{BC}} \\ {\dfrac{8}{1}} & = & {\dfrac{EF}{\sqrt{3}}} \\ {8\sqrt{3}} & = & {EF} \end{array}\)
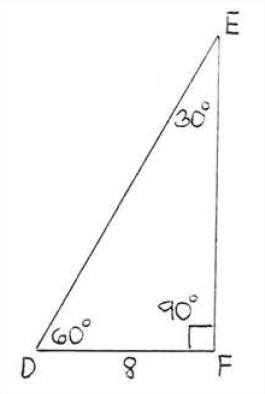
Our conclusions about triangles \(ABC\) and \(DEF\) suggest the following theorem:
In the \(30^{\circ} -60^{\circ}-90^{\circ}\) triangle the hypotenuse is always twice as large as the leg opposite the \(30^{\circ}\) angle (the shorter leg). The leg opposite the \(60^{\circ}\) angle (the longer leg) is always equal to the shorter leg times \(\sqrt{3}\).
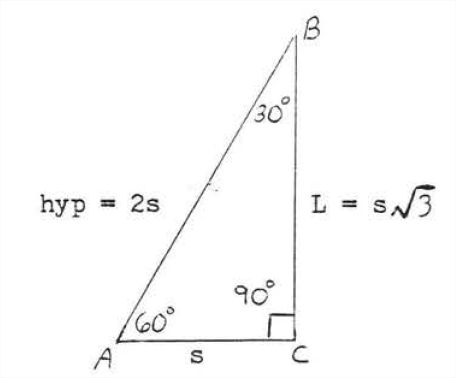
In Figure \(\PageIndex{5}\), \(s =\) shorter leg, \(L =\) longer leg, and hyp = hypotenuse. Theorem \(\PageIndex{1}\) says that
\[\boxed{ \begin{align*} \text{hyp} &= 2s \\[4pt] L &= s\sqrt{3} \end{align*}}\]
Note that the longer leg is always the leg opposite (furthest away from) the \(60^{\circ}\) angle and the shorter leg is always the leg opposite (furthest away from) the \(30^{\circ}\) angle.
Find \(x\) and \(y\):

Solution
\(\angle B = 180^{\circ} - (60^{\circ} + 90^{\circ}) = 180^{\circ} - 150^{\circ} = 30^{\circ}\), so \(\triangle ABC\) is a \(30^{\circ} - 60^{\circ} - 90^{\circ}\) triangle. By theorem \(\PageIndex{1}\),
\(\begin{array} {rcl} {\text{hyp}} & = & {2s} \\ {y} & = & {2(7) = 14.} \end{array}\) \(\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {x} & = & {7\sqrt{3}} \end{array}\)
Answer
\(x = 7\sqrt{3}\), \(y = 14\).
Find \(x\) and \(y\):
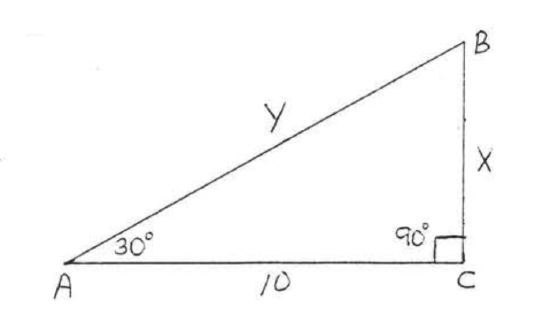
Solution
\(\angle B = 60^{\circ}\) so \(\triangle ABC\) is a \(30^{\circ} - 60^{\circ}-90^{\circ}\) triangle. By Theorem \(\PageIndex{1}\),
\(\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {10} & = & {x\sqrt{3}} \\ {\dfrac{10}{\sqrt{3}}} & = & {\dfrac{x\cancel{\sqrt{3}}}{\cancel{\sqrt{3}}}} \\ {x} & = & {\dfrac{10}{\sqrt{3}} = \dfrac{10}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}} = \dfrac{10\sqrt{3}}{3}.} \\ {\text{hyp}} & = & {2s} \\ {y} & = & {2x = 2(\dfrac{10\sqrt{3}}{3}) = \dfrac{20\sqrt{3}}{3}} \end{array}\)
Answer
\(x = \dfrac{10\sqrt{3}}{3}, y = \dfrac{20\sqrt{3}}{3}\).
45°−45°−90° Right Triangles
The second special triangle we will consider is the \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle. A triangle whose angles are \(45^{\circ}\), \(45^{\circ}\), and \(90^{\circ}\) is called a \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle or an isosceles right triangle. \(\triangle ABC\) in Figure \(\PageIndex{6}\) is a \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle with side \(AC = 1\).
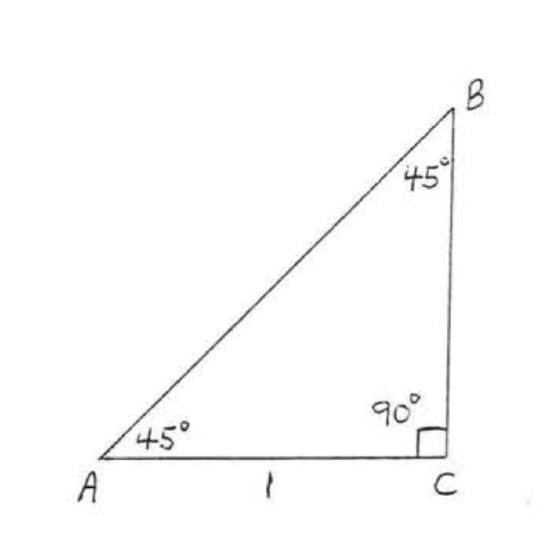
Since \(\angle A = \angle B = 45^{\circ}\), the sides opposite these angles must be equal (Theorem 2.5.2, Section 2.5). Therefore \(AC = BC = 1\).
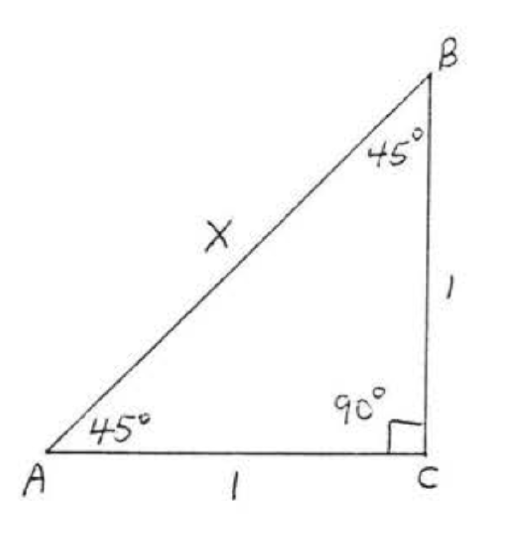
Let \(x = AB\) (Figure \(\PageIndex{7}\)). By the Pythagorean Theorem,
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {1^2 + 1^2} & = & {x^2} \\ {1 + 1} & = & {x^2} \\ {2} & = & {x^2} \\ {\sqrt{2}} & = & {x} \end{array}\)
Find \(x\):
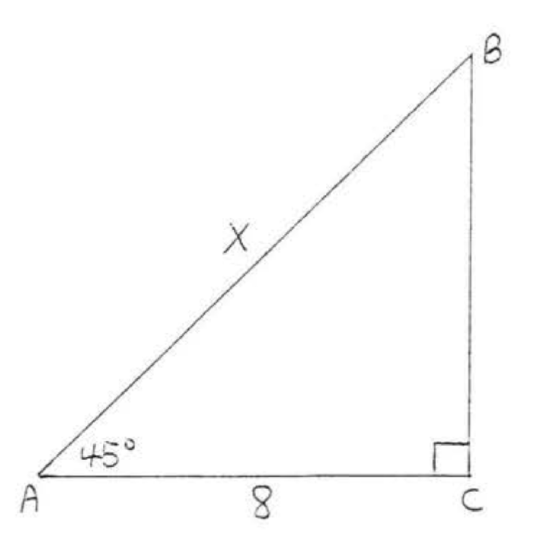
Solution
\(\angle B = 180^{\circ} - (45^{\circ} + 90^{\circ}) = 180^{\circ} - 135^{\circ} = 45^{\circ}\). So \(\triangle ABC\) is a \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle. \(AC = BC = 8\) because these sides are opposite equal angles. By the Pythagorean Theorem,
\(\begin{array} {rcl} {\text{leg}^2 + \text{leg}^2} & = & {\text{hyp}^2} \\ {8^2 + 8^2} & = & {x^2} \\ {64 + 64} & = & {x^2} \\ {128} & = & {x^2} \\ {x} & = & {\sqrt{128} = \sqrt{64} \sqrt{2} = 8 \sqrt{2}} \end{array}\)
Answer
\(x = 8\sqrt{2}\).
The triangles of Figure \(\PageIndex{6}\) and Example \(\PageIndex{3}\) suggest the following theorem:
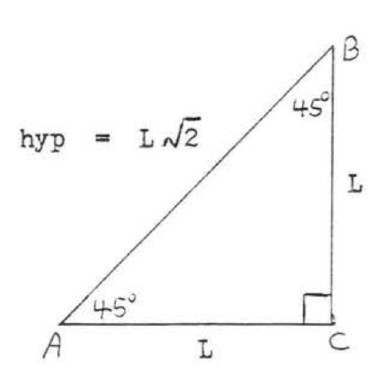
In the \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle the legs are equal and the hypotenuse is equal to either leg times \(\sqrt{2}\).
In Figure \(\PageIndex{8}\), \(\text{hyp}\) is the hypotenuse and \(L\) is the length of each leg. Theorem \(\PageIndex{2}\) says that
\[ \boxed{ \text{hyp} = \sqrt{2} L } \]
Find \(x\) and \(y\):
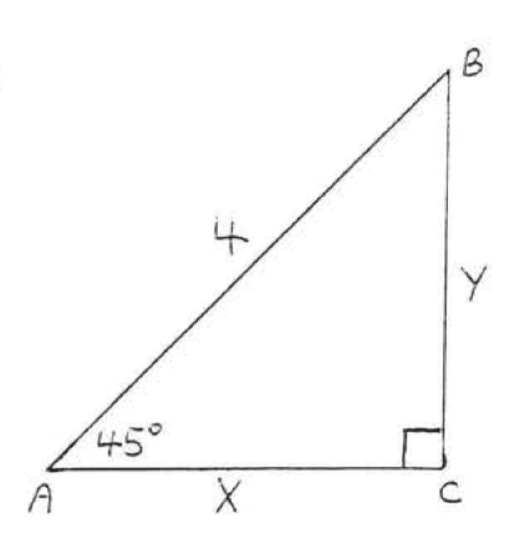
Solution
\(\angle B = 45^{\circ}\). So \(\triangle ABC\) is an isosceles right triangle and \(x = y\).
\(\begin{array} {rcl} {x^2 + y^2} & = & {4^2} \\ {x^2 + x^2} & = & {16} \\ {2x^2} & = & {16} \\ {x^2} & = & {8} \\ {x} & = & {\sqrt{8} = \sqrt{4} \sqrt{2} = 2\sqrt{2}} \end{array}\)
Answer: \(x = y = 2 \sqrt{2}\).
Another method:
\(\triangle ABC\) is a \(45^{\circ}-45^{\circ} -90^{\circ}\) triangle. Hence by Theorem \(\PageIndex{2}\),
\(\begin{array} {rcl} {\text{hyp}} & = & {L\sqrt{2}} \\ {4} & = & {x\sqrt{2}} \\ {\dfrac{4}{\sqrt{2}}} & = & {\dfrac{x\cancel{\sqrt{2}}}{\cancel{\sqrt{2}}}} \\ {x} & = & {\dfrac{4}{\sqrt{2}} = \dfrac{4}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}} = \dfrac{4\sqrt{2}}{2} = 2\sqrt{2}} \end{array}\)
Answer
\(x = y = 2\sqrt{2}\).
Find \(AB\):
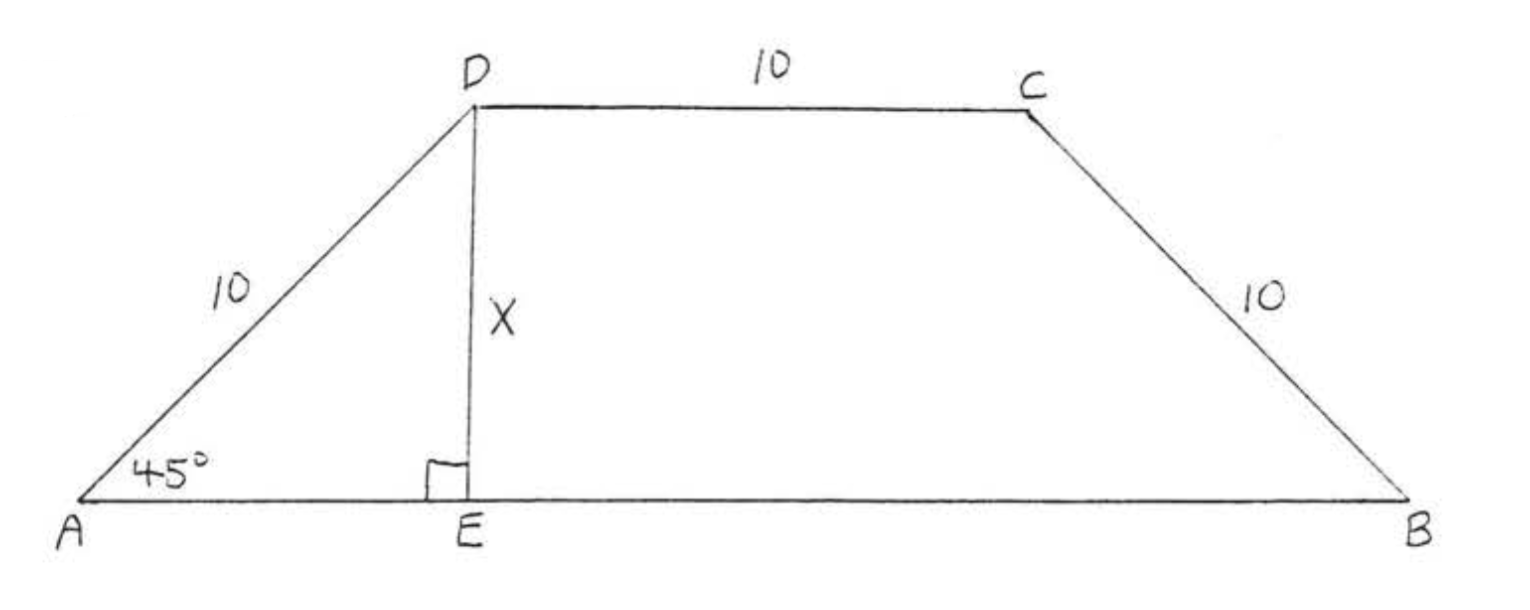
Solution
\(\triangle ADE\) is a \(45^{\circ}-45^{\circ}-90^{\circ}\) triangle. Hence
\(\begin{array} {rcl} {\text{hyp}} & = & {L \sqrt{2}} \\ {10} & = & {x\sqrt{2}} \\ {\dfrac{10}{\sqrt{2}}} & = & {\dfrac{x\cancel{\sqrt{2}}}{\cancel{\sqrt{2}}}} \\ {x} & = & {\dfrac{10}{\sqrt{2}} = \dfrac{10}{\sqrt{2}} \cdot \dfrac{\sqrt{2}}{\sqrt{2}} = \dfrac{10\sqrt{2}}{2} = 5\sqrt{2}} \\ {AE = x} & = & {5\sqrt{2}} \end{array}\)
Now draw \(CF\) perpendicular to \(AB\) (Figure \(\PageIndex{9}\)). \(\angle B = 45^{\circ}\) since \(ABCD\) is an isosceles trapezoid (Theorem 3.2.4, Section 3.2).
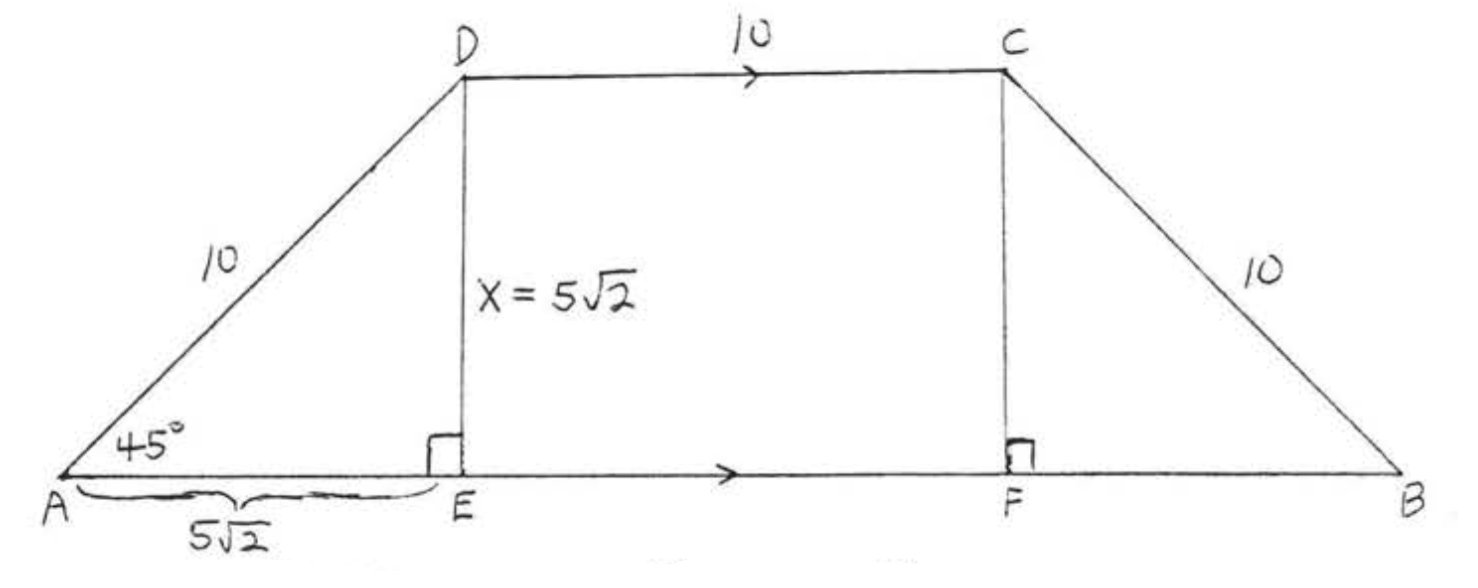
So \(\triangle BCF\) is a \(45^{\circ}-45^{\circ}-90^{\circ}\) triangle congruent to \(\triangle ADE\) and therefore \(BF = 5 \sqrt{2}\). \(CDEF\) is a rectangle and therefore \(EF = 10\). We have \(AB = AE + EF + FB = 5\sqrt{2} + 10 + 5\sqrt{2} = 10\sqrt{2} + 10\).
Answer
\(AB = 10\sqrt{2} + 10\).
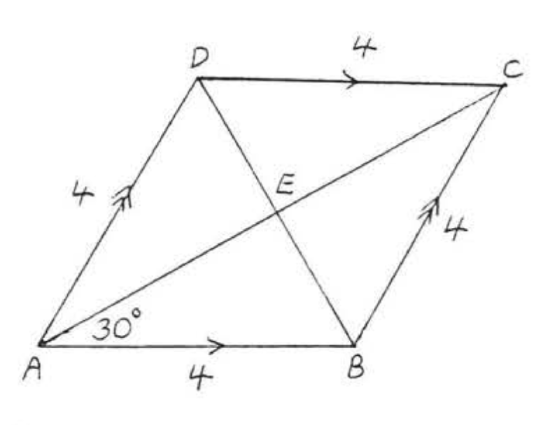
Find \(AC\) and \(BD\):
Solution
\(ABCD\) is a rhombus. The diagonals \(AC\) and \(BD\) are perpendicular and bisect each other. \(\angle AEB = 90^{\circ}\) and \(\angle ABE = 180^{\circ} - (90^{\circ} - 30^{\circ}) = 60^{\circ}\). So \(\triangle AEB\) is a \(30^{\circ}-60^{\circ}-90^{\circ}\) triangle.
\(\begin{array} {rcl} {\text{hyp}} & = & {2s} \\ {4} & = & {2(BE)} \\ {2} & = & {BE} \\ {bd} & = & {2 + 2 = 4} \end{array}\) \(\begin{array} {rcl} {L} & = & {s\sqrt{3}} \\ {AE} & = & {2\sqrt{3}} \\ {AC} & = & {2\sqrt{3} + 2\sqrt{3}} \\ {AC} & = & {4\sqrt{3}} \end{array}\)
Answer
\(AC = 4\sqrt{3}, BD = 4\).
The Pythagoreans believed that all physical relation ships could be expressed with whole numbers. However the sides of the special triangles described in this section are related by irrational numbers, \(\sqrt{2}\) and \(\sqrt{3}\). An irrational number is a number which can be approximated, but not expressed exactly, by a ratio of whole numbers. For example \(\sqrt{2}\) can be approximated with increasing accuracy by such ratios as \(1.4 = \frac{14}{10}\), \(1.41 = \frac{141}{100}\), \(1.414 = \frac{1414}{1000}\), etc., but there is no fraction of whole numbers which is exactly equal to \(\sqrt{2}\). (For more details and a proof, see the book by Richardson listed in the References). The Pythagoreans discovered that \(\sqrt{2}\) was irrational in about the 5th century B.C. It was a tremendous shock to them that not all triangles could be measured "exactly." They may have even tried to keep this discovery a secret for fear of the damage it would do to their philosophical credibility.
The inability of the Pythagoreans to accept irrational numbers had unfortunate consequences for the development of mathematics. Later Greek mathematicians avoided giving numerical values to lengths of line segments. Problems whose algebraic solutions might be irrational numbers, such as those involving quadratic equations, were instead stated and solved geometrically. The result was that geometry flourished at the expense of algebra. It was left for the Hindus and the Arabs to resurrect the study of algebra in the Middle Ages. And it was not until the 19th century that irrational numbers were placed in the kind of logical framework that the Greeks had given to geometry 2000 years before.
Problems
1 - 10. Find \(x\) and \(y\):
1.
2.
3.
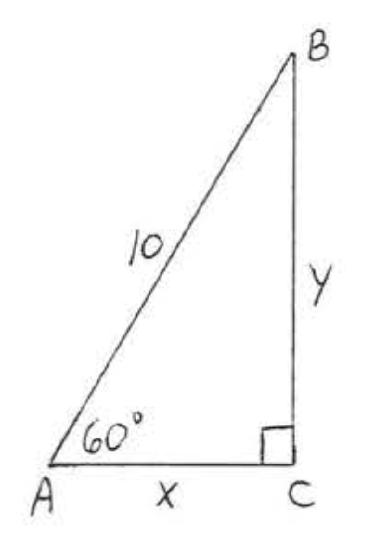
4.
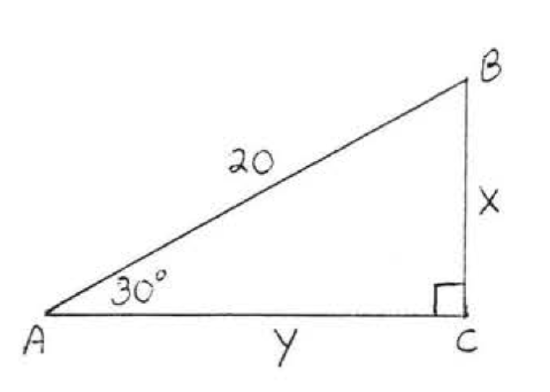
5.
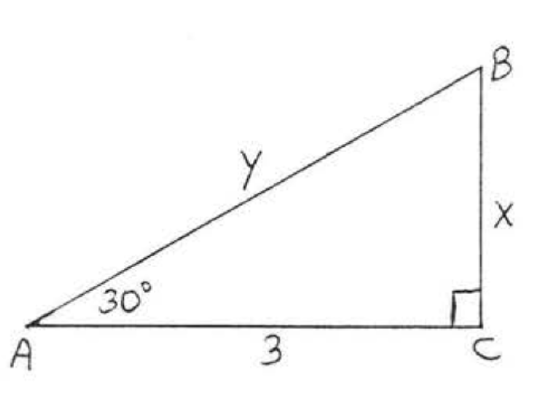
6.
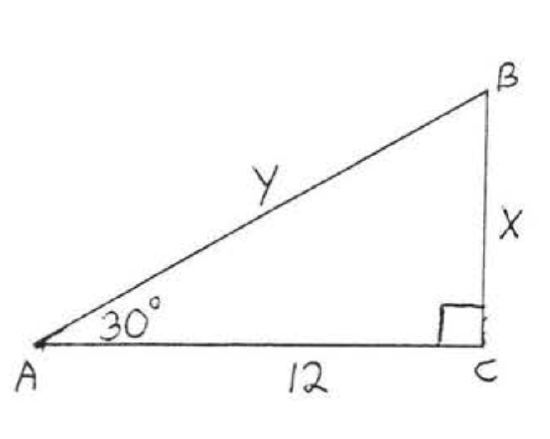
7.
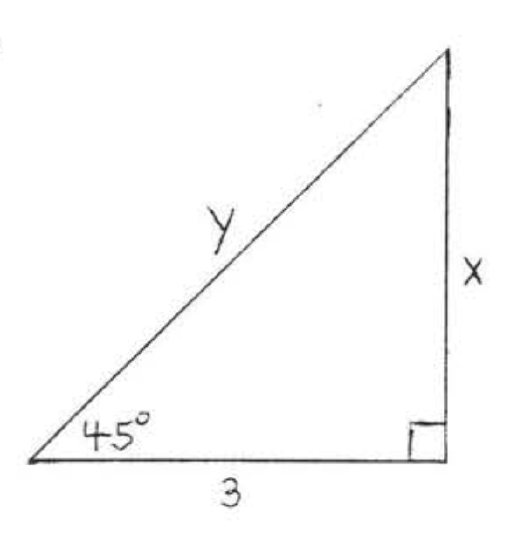
8.
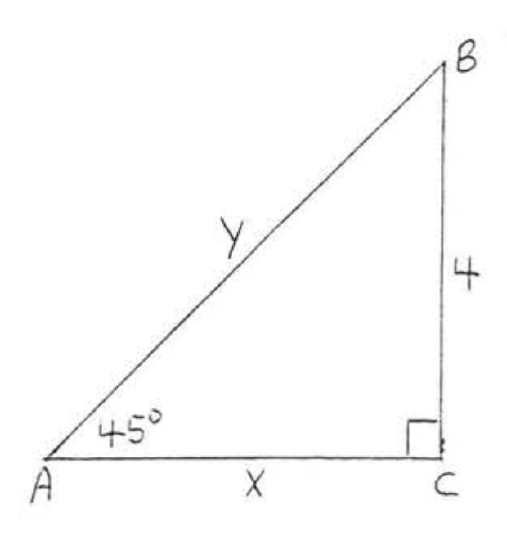
9.
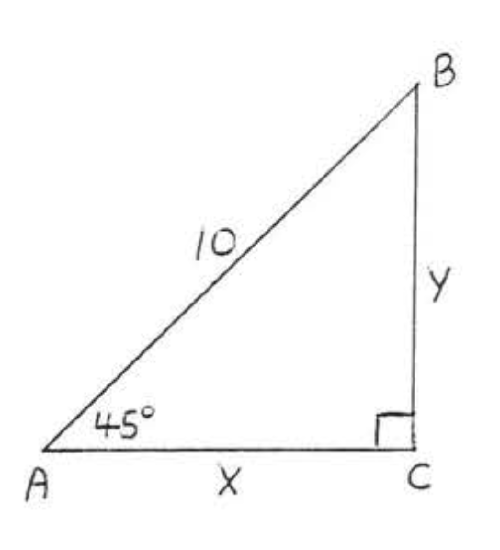
10.
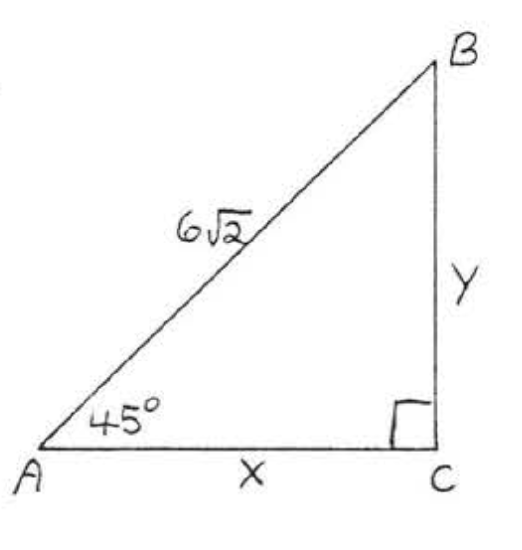
11 - 14. Find \(x\):
11.
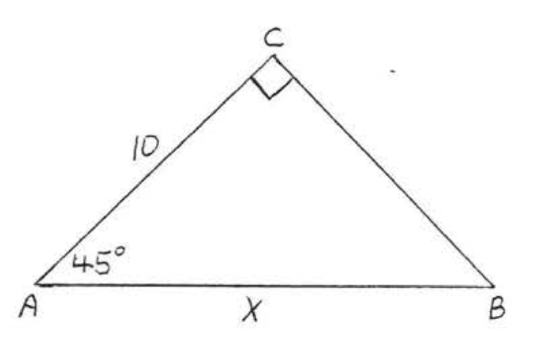
12.
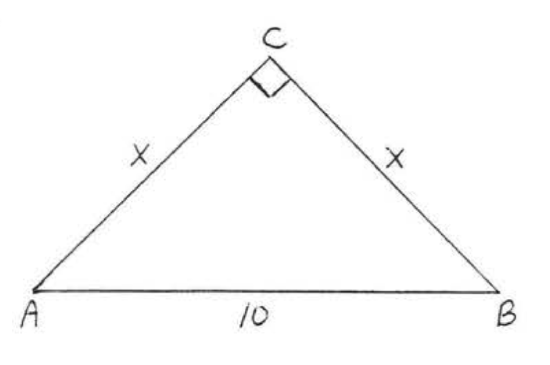
13.
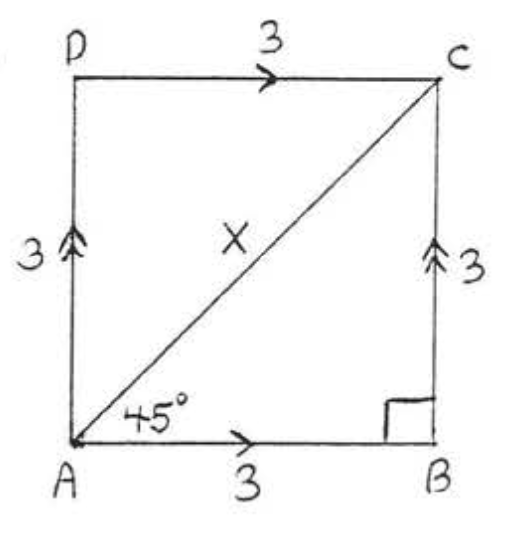
14.
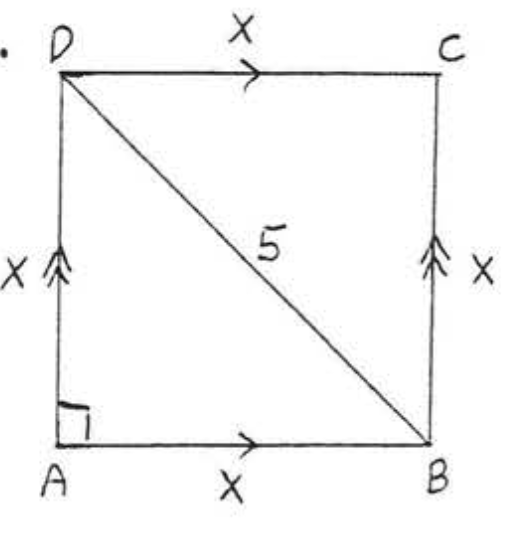
15 - 20. Find \(x\) and \(y\):
15.
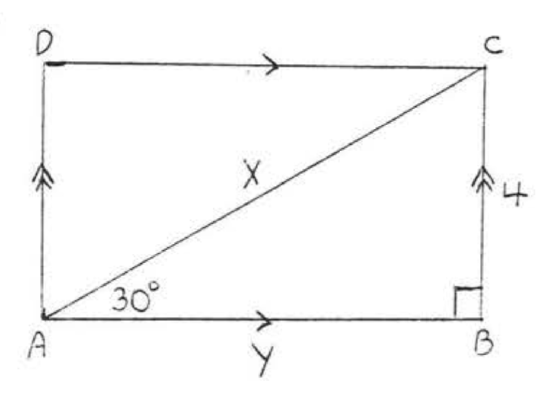
16.
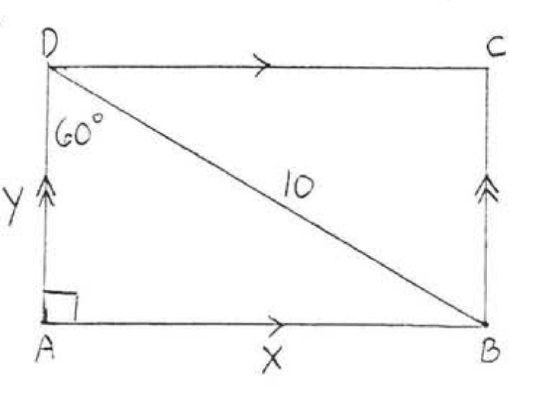
17.
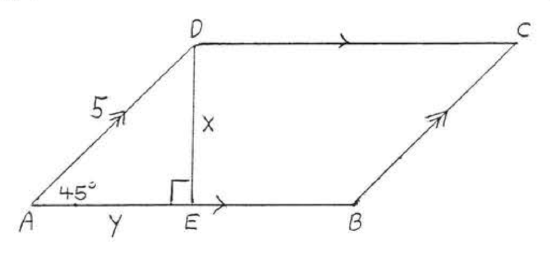
18.
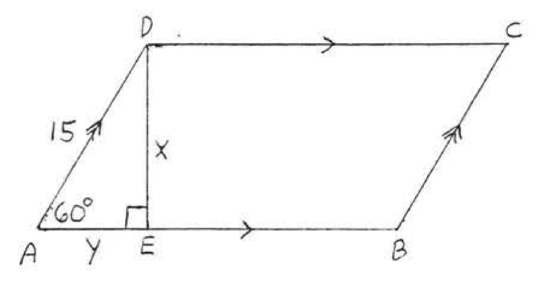
19.
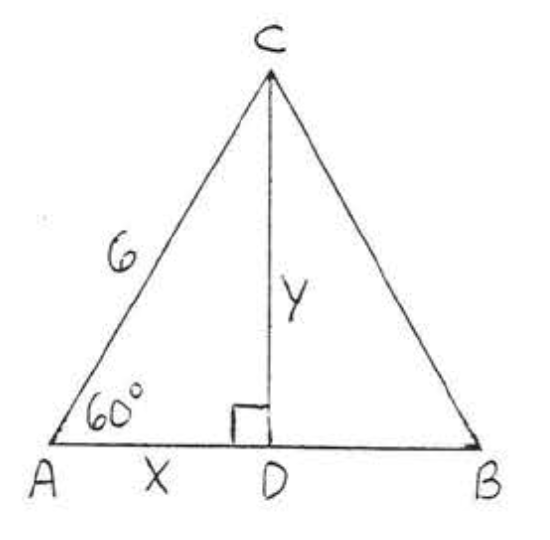
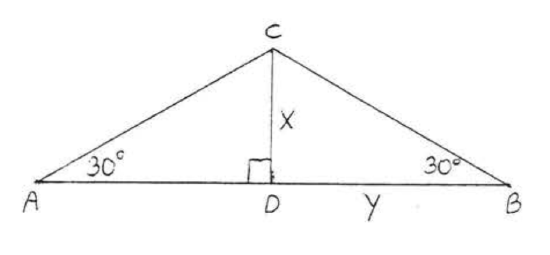
20.
21 - 22. Find \(x\) and \(AB\):
21.
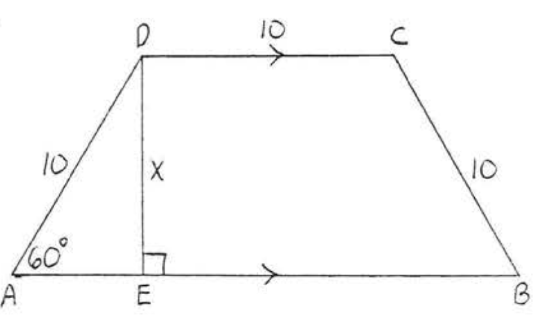
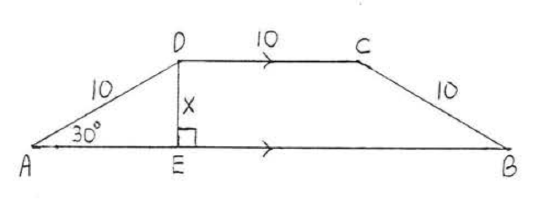
22.
23 - 24. Find \(x\) and \(y\):
23.
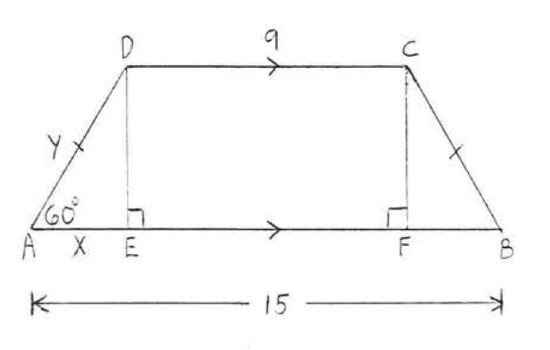
24.
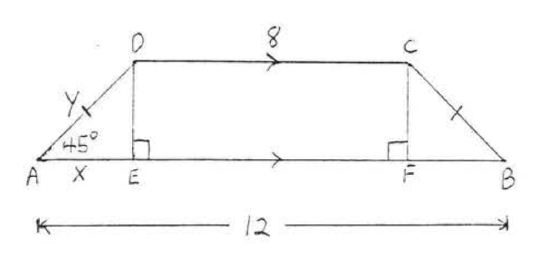
25. Find \(AC\) and \(BD\):
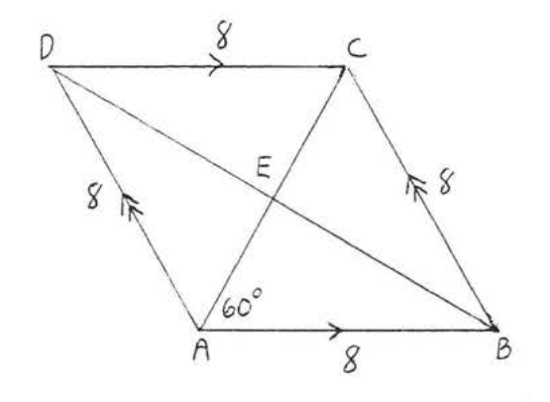
26. Find \(x, AC\) and \(BD\):



