4.6: Distance from a Point to a Line
( \newcommand{\kernel}{\mathrm{null}\,}\)
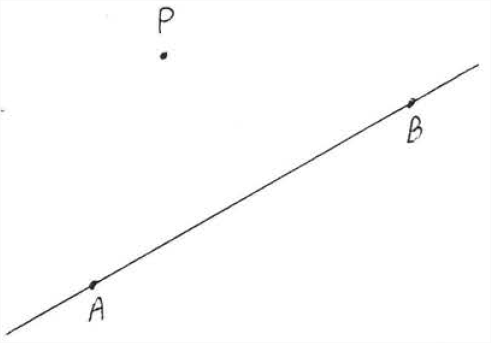
Suppose we are given a point P and a line ↔AB as in Figure 4.6.1. We would like to find the shortest line segment that can be drawn from P to ↔AB.
First we will prove a theorem:
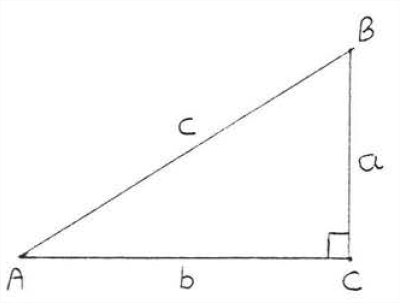
In a right triangle, the hypotenuse is larger than either leg. In Figure 4.6.1, c>a and c>b. (The symbol ">" means "is greater than.")
- Proof
-
By the Pythagorean Theorem,
c=√a2+b2>√a2=a.
c=√a2+b2>√b2=b.
Now we can give the answer to our question:
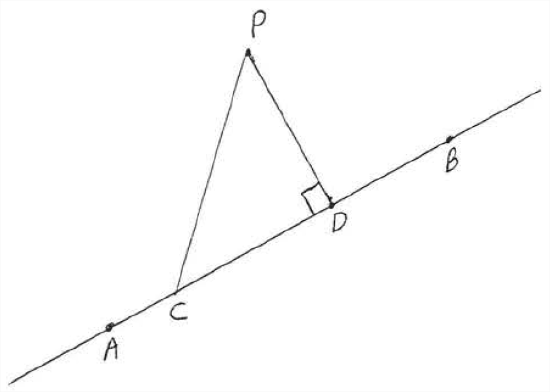
The perpendicular is the shortest line segment that can be drawn from a point to a straight line.
In Figure 4.6.3 the shortest line segment from P to ↔AB is PD. Any other line segment, such as PC, must be longer.
- Proof
-
PC is the hypotenuse of right triangle PCD. Therefore by Theorem 4.6.1, PC>PD.
We define the distance from a point to a line to be the length of the perpendicular.
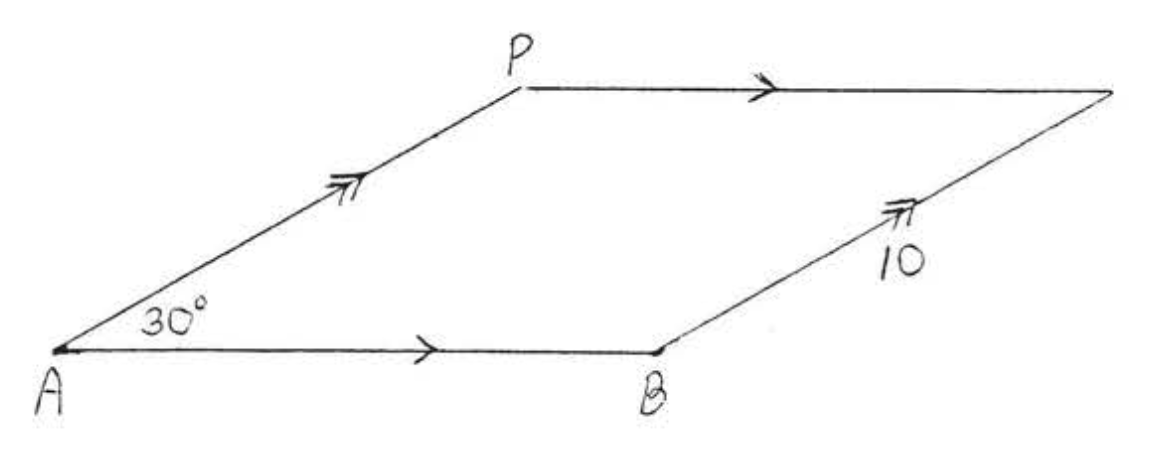
Find the distance from P to ↔AB:
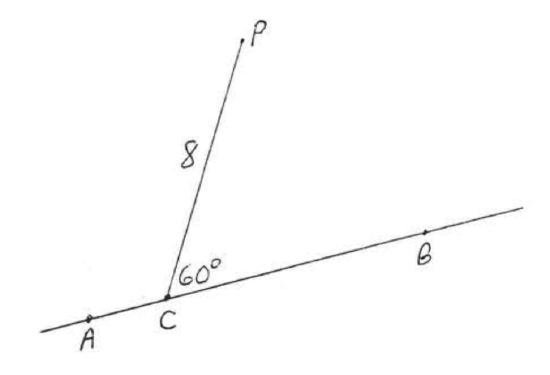
Solution
Draw PD perpendicular to ↔AB (Figure 4.6.4). △PCD is a 30∘−60∘−90∘ triangle.
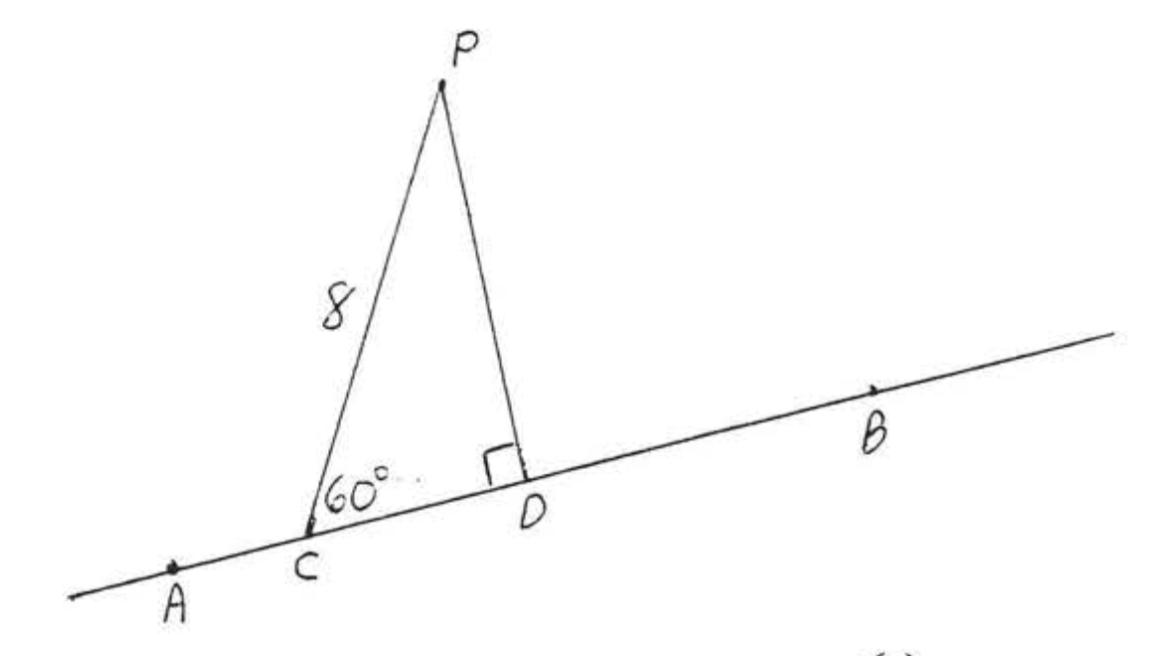
hyp=2s8=2(CD)4=CDL=s√3PD=4√3
Answer: 4√3
Problems
1 - 6. Find the distance from P to ↔AB:
1.
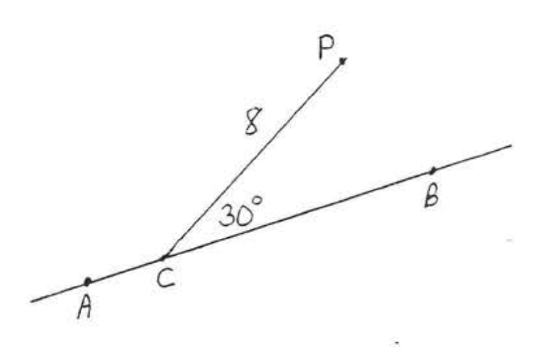
2.
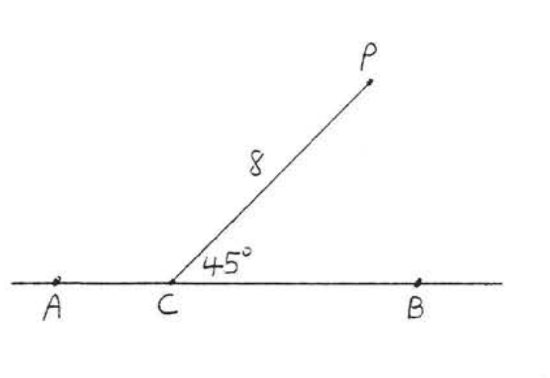
3.
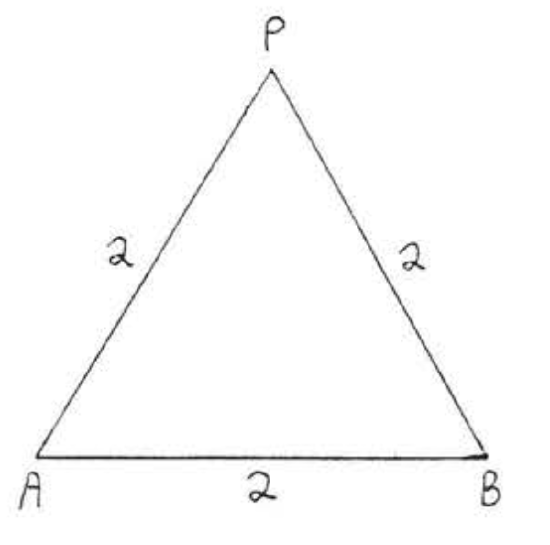
4.
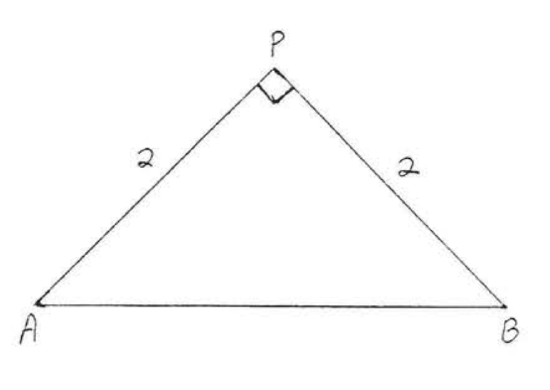
5.
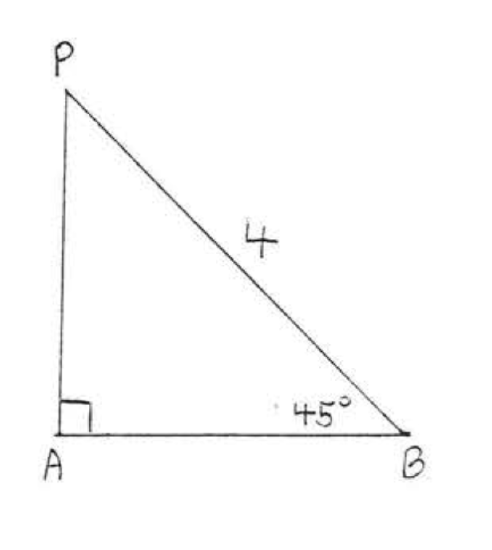
6.