7.1: Regular Polygons
- Page ID
- 34152
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A regular polygon is a polygon in which all sides are equal and all angles are equal, Examples of a regular polygon are the equilateral triangle (3 sides), the square (4 sides), the regular pentagon (5 sides), and the regular hexagon (6 sides). The angles of a regular polygon can easily be found using the methods of section 1.5.
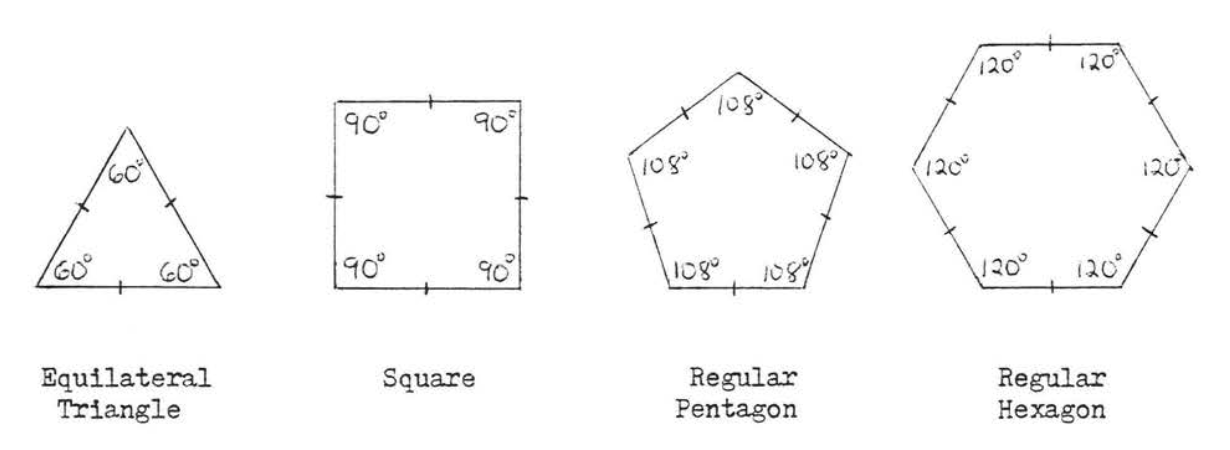
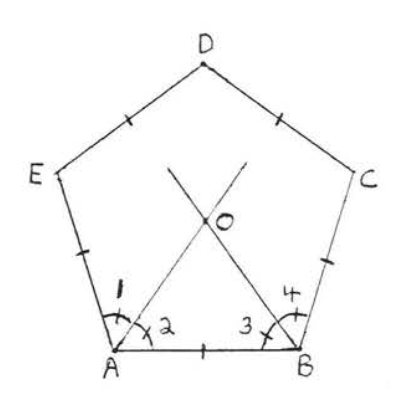
Suppose we draw the angle bisector of each angle of a regular polygon, We will find these angle bisectors all meet at the same point (Figure \(\PageIndex{2}\)).
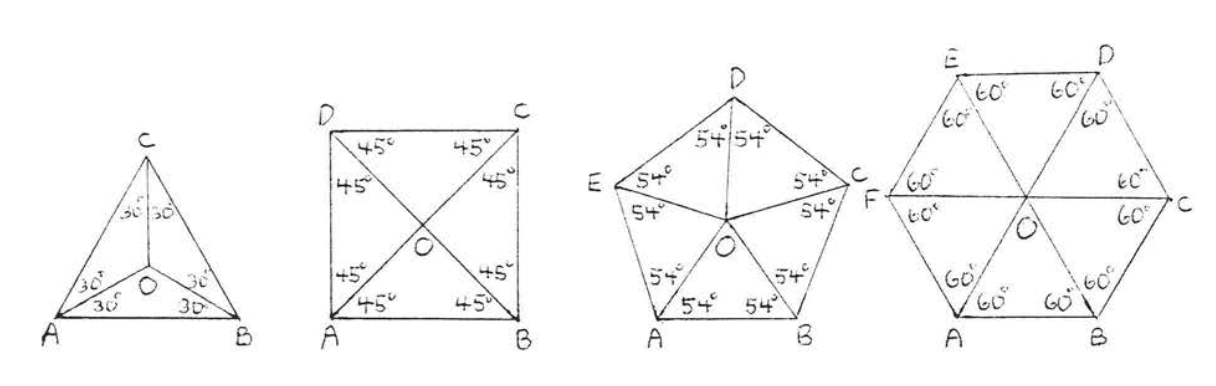
The angle bisectors of each angle of a regular polygon meet at the same point. This point is called the center of the regular polygon.
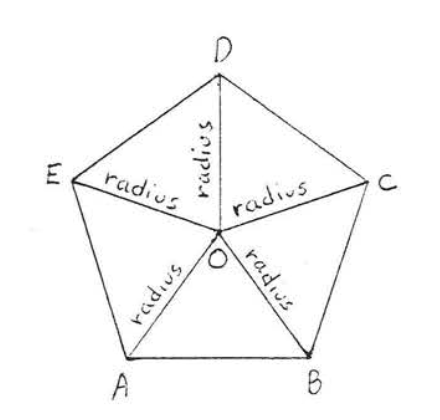
In Figure \(\PageIndex{2}\). \(O\) is the center of each regular polygon. The segment of each angle bisector from the center to the vertex is called a radius. For example, \(OA, OB, OC, OD\), and \(OE\) are the five radii of regular pentagon \(ABCDE\).
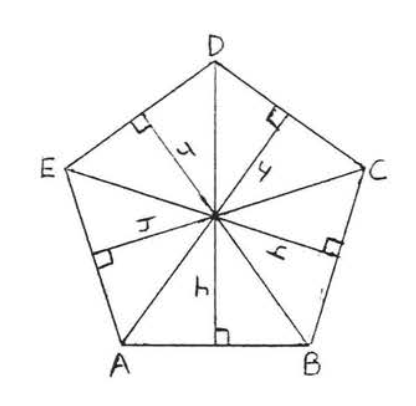
The radii of a regular polygon divide the polygon into congruent isosceles triangles. All the radii are equal.
In Figure \(\PageIndex{3}\), radii \(OA, OB, OC, OD\), and \(OE\) divide the regular pentagon into five isosceles triangles with \(OA = OB =OC = OD = OE\).
Find the radius \(CA\), and the angles \(x^{\circ}\), \(y^{\circ}\), and \(z^{\circ}\) in the regular octagon (eight-sided figure):
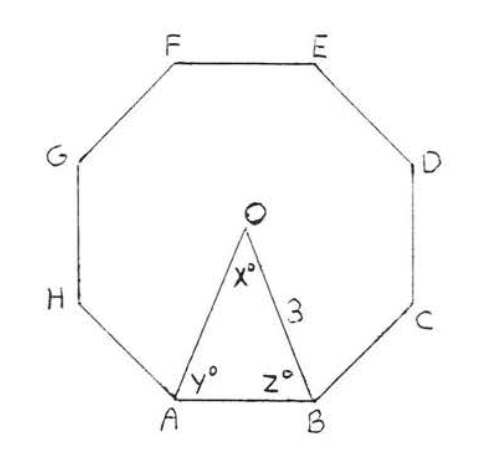
Solution
The radii divide the octagon into 8 congruent isosceles triangles. Therefore \(OA = OB = 3\).
\(x^{\circ} = \dfrac{1}{8} (360^{\circ}) = 45^{\circ}\).
\(y^{\circ}= z^{\circ} = \dfrac{1}{2}(180^{\circ} - 45^{\circ}) = \dfrac{1}{2} (135^{\circ}) = 67 \dfrac{1}{2}^{\circ}\).
Answer: \(OA = 3, x^{\circ} = 45^{\circ}, y^{\circ} = z^{\circ} = 67 \dfrac{1}{2}^{\circ}\).
Theorem \(\PageIndex{1}\) and Theorem \(\PageIndex{2}\) appear to be true intuitively, but we verify them with a formal proof:
Proof of Theorem \(\PageIndex{1}\) and Theorem \(\PageIndex{2}\): We will prove these theorems for the regular pentagon. The proof for other regular polygons is similar.
Draw the angle bisectors of \(\angle A\) and \(\angle B\) as in Figure \(\PageIndex{4}\) and call their point of intersection \(O\). We will show \(OC, OD\), and \(OE\) are the angle bisectors of \(\angle C\), \(\angle D\), and \(\angle E\) respectively.
\(\angle EAB = \angle ABC\) since the angles of a regular pentagon are equal. \(\angle 1 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle ABC = \angle 3 = \angle 4\) since \(OA\) and \(OB\) are angle bisectors.
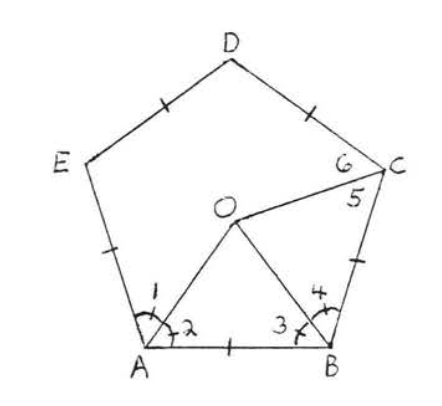
Draw \(OC\) (Figure \(\PageIndex{5}\)). \(AB = BC\) since the sides of a regular pentagon are equal. Therefore \(\triangle AOB \cong \triangle COB\) by \(SAS = SAS\). Therefore \(\angle 5 = \angle 2 = \dfrac{1}{2}\) of \(\angle EAB = \dfrac{1}{2}\) of \(\angle BCD\). So \(OC\) is the angle bisector of \(\angle BCD\).
Similarly we can show \(\triangle BOC \cong \triangle DOC\), \(\triangle COD \cong \triangle EOD\), \(\triangle DOE \cong \triangle AOE\) and that \(OD\) and \(OE\) are angle bisectors. The triangles are all isosceles because their base angles are equal. This completes the proof.
A line segment drawn from the center perpendicular to the sides of a regular polygon is called an apothem (see Figure \(PageIndex{6}\)).
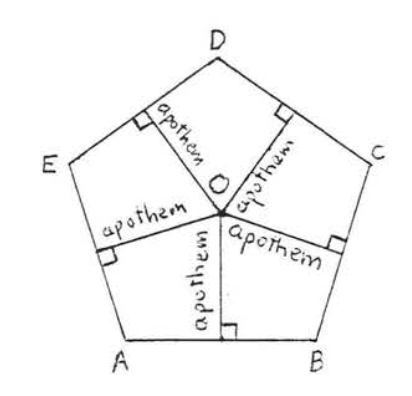
The apothems of a regular polygon are all equal, They bisect the sides of the regular polygon.
- Proof
-
The apothems are all equal because they are the heights of the congruent isosceles triangles formed by the radii (see Theorem \(\PageIndex{2}\)), Each apothem divides the isosceles triangle into two congruent right triangles, Therefore each apothem bisects a side of the polygon, which is what we wanted to prove.
Find the apothem of a regular pentagon with side 20, to the nearest tenth.
Solution
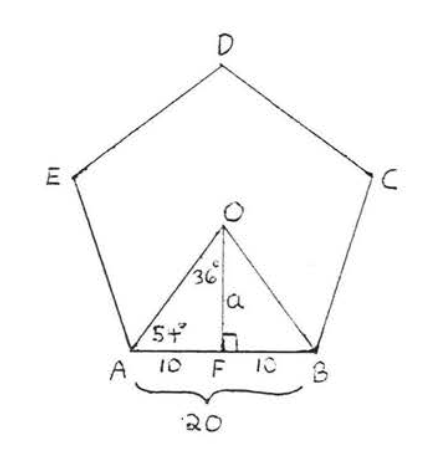
In Figure \(\PageIndex{8}\),
\(\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ}\),
\(\angle AOF = \dfrac{1}{2}\angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}\),
and \(\angle OAF = 90^{\circ} - 36^{\circ} = 54^{\circ}\).
\(\begin{array} {rcl} {\tan 54^{\circ}} & = & {\dfrac{a}{10}} \\ {(10)1.3764} & = & {\dfrac{a}{10}(10)} \\ {13.764} & = & {a} \\ {13.8} & = & {a} \end{array}\)
Answer: 13.8
The apothem of a regular polygon is important because it is used to find the area:
The area of a regular polygon is one-half the product of the apothem and the perimeter.
\[A = \dfrac{1}{2} a P\]
- Proof
-
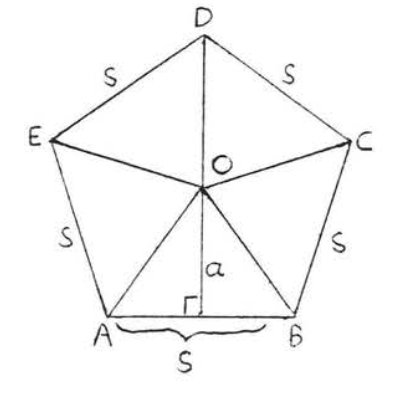
Figure \(PageIndex{9}\). The area of \(\triangle AOB\) is \(\dfrac{1}{2}\) as, where \(s\) is the side of the pentagon. We prove the Theorem for the regular pentagon. The proof for other regular polygons is similar.
The radii of a regular pentagon divide the regular pentagon into five congruent triangles. The area of each triangle is \(\dfrac{1}{2}\) as, where \(s\) is the side of the pentagon (Figure \(PageIndex{9}\)). Therefore, area of the pentagon = 5(\dfrac{1}{2} as) = \dfrac{1}{2} a (5s) = \dfrac{1}{2}aP\), which is the formula we wanted to prove.
Find the area of a regular pentagon with side 20, to the nearest tenth.
Solution
From Example \(\PageIndex{2}\) we know \(a = 13.764\). The perimeter \(P = (5)(20) = 100\). Therefore \(A = \dfrac{1}{2} aP = \dfrac{1}{2} (13.764)(100) = \dfrac{1}{2} (1376.4) = 688.2\).
Answer: 688.2
To find the perimeter of a regular polygon, all we have to do is to multiply the length of a side by the number of sides. For example, the pentagon of Figure \(\PageIndex{8}\) has perimeter \(P = 5(20)=100\). However it is also useful to have a formula for the perimeter when only the radius is known:
The perimeter of a regular polygon of \(n\) sides with radius \(r\) is given by the formula
\[P = 2 rn \sin \dfrac{180^{\circ}}{n}\]
- Proof
-
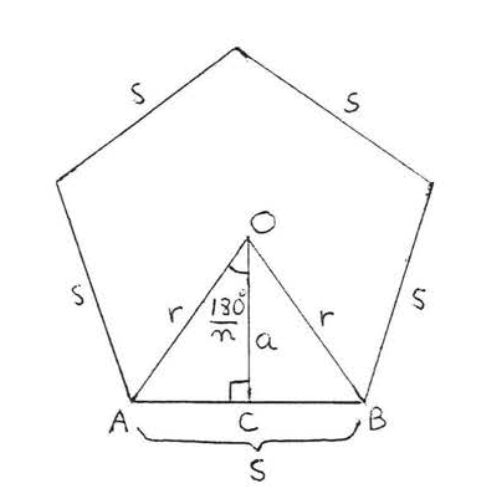
Figure \(\PageIndex{10}\): A regular polygon with radius \(r\) and side \(s\). Let us label the regular polygon as in Figure \(PageIndex{10}\). Since the radii of the regular polygon divide the polygon into \(n\) congruent triangles (Theorem \(\PageIndex{2}\)), we have
\(\angle AOB = \dfrac{1}{n} (360^{\circ}) = \dfrac{360^{\circ}}{n}.\)
By Theorem \(\PageIndex{3}\) apothem \(OC\) divides \(AOB\) into two congruent right triangles, so
\(\angle AOC = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (\dfrac{360^{\circ}}{n}) = \dfrac{180^{\circ}}{n}.\)
Applying trigonometry to right triangle \(AOC\) we have
\(\begin{array} {rcl} {\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r}} \\ {(r)\sin \dfrac{180^{\circ}}{n}} & = & {\dfrac{AC}{r} (r)} \\ {r \sin \dfrac{180^{\circ}}{n}} & = & {AC} \end{array}\)
Since \(OC\) bisects \(AB\),
\(s = 2(AC)= 2r\sin \dfrac{180^{\circ}}{n}\)
and therefore
\(P = ns = n(2r \sin \dfrac{180^{\circ}}{n}) = 2rn \sin \dfrac{180^{\circ}}{n}\)
which is the formula that we wish to prove.
Find the perimeter of a regular pentagon with radius 10, to the nearest tenth.
Solution
A pentagon has \(n = 5\) sides. Using the formula of Theorem \(\PageIndex{5}\), \(P = 2rn \sin \dfrac{180^{\circ}}{n} = 2(10)(5) \sin \dfrac{180^{\circ}}{5} = 100 \sin 36^{\circ} = 100(.5878) = 58.78 = 58.8.\)
Answer: 58.8.
He can also give explicit formulas for the various regular polygons, as in the following table:
| Regular Figure | \(n\) | \(n \sin \dfrac{180^{\circ}}{n}\) | \(P = 2 rn \sin \dfrac{180^{\circ}}{n}\) |
|---|---|---|---|
| Triangle | 3 | \(3 \sin 60^{\circ} = 2.5980\) | \(5.1960\ r\) |
| Square | 4 | \(4 \sin 45^{\circ} = 2.8284\) | \(5.6568\ r\) |
| Pentagon | 5 | \(5 \sin 36^{\circ} = 2.9390\) | \(5.8780\ r\) |
| Hexagon | 6 | \(6 \sin 30^{\circ} = 3.0000\) | \(6.0000\ r\) |
| Decagon | 10 | \(10 \sin 18^{\circ} = 3.090\) | \(6.180\ r\) |
| 45-sided figure | 45 | \(45 \sin 4^{\circ} = 3.139\) | \(6.278\ r\) |
| 90-sided figure | 90 | \(90 \sin 2^{\circ} = 3.141\) | \(6.282\ r\) |
| 1000-sided figure | 1000 | \(1000 \sin 180^{\circ} = 3.1416\) | \(6.283\ r\) |
From Table \(\PageIndex{1}\) we can see that as the number of sides increases, the perimeter of a regular polygon becomes approximately 6.28 times the radius. You may also recognize that the value of \(n \sin \dfrac{180^{\circ}}{n}\) comes close to the number \(\pi\). We will return to this point when we discuss the circumference of a circle in section 7.5.
Find the perimeter of a regular pentagon Hith radius 10, to the nearest tenth.
Solution
From the table
\[ \begin{align*} P &= 5.8780\ r \\[4pt] &= 5.8780(10) \\[4pt] &= 58.78 \\[4pt] &= 58.8 \end{align*}.\]
Answer: 58.8.
Find the apothem and area of a regular pentagon with radius 10, to the nearest tenth.
Solution
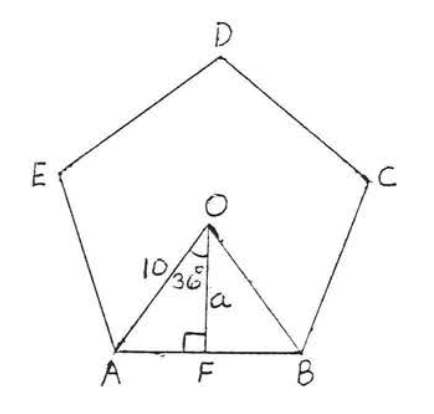
In Figure \(\PageIndex{11}\)
\[\angle AOB = \dfrac{1}{5} (360^{\circ}) = 72^{\circ} \nonumber\]
and
\[\angle AOF = \dfrac{1}{2} \angle AOB = \dfrac{1}{2} (72^{\circ}) = 36^{\circ}. \nonumber\]
Applying trigonometry to right triangle \(AOF\),
\(\begin{array} {rcl} {\cos 36^{\circ}} & = & {\dfrac{a}{10}} \\ {(10).8090} & = & {\dfrac{a}{10}(10)} \\ {8.090} & = & {a} \end{array}\)
From Example \(\PageIndex{4}\), \(P = 58.78\). Therefore, by Theorem \(\PageIndex{4}\),
\(A = \dfrac{1}{2} a P = \dfrac{1}{2} (8.09) (58.78) = \dfrac{1}{2} (475.5302) = 237.7651 = 237.8.\)
Answer: \(a = 8.1, P = 237.8\).
In 1936 archeologists unearthed a group of ancient Babylonian tables containing formulas for the areas of regular polygons of three, four, five, six and seven sides, There is evidence that regular polygons were commonly used in the architecture and designs of other ancient civilizations as well, A classical problem of Greek mathematics was to construct a regular polygon using just a ruler and compass, Regular polygons were usually studied in relationship to circles. As we shall see later in this chapter, the formulas for the area and perimeter of a circle can be derived from the corresponding formulas for regular polygons.
Problems
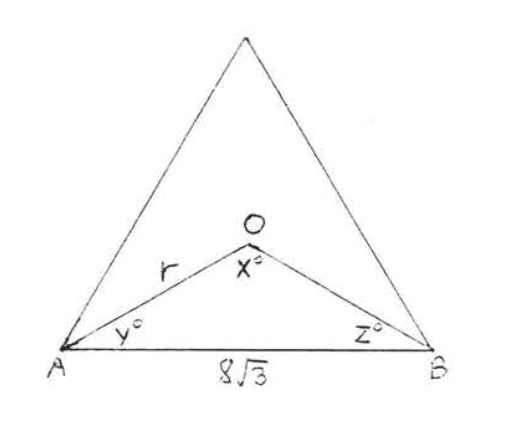
1 - 6. Find the angles \(x^{\circ}, y^{\circ}, z^{\circ}\) and radius \(r\) of the regular polygons:
1.
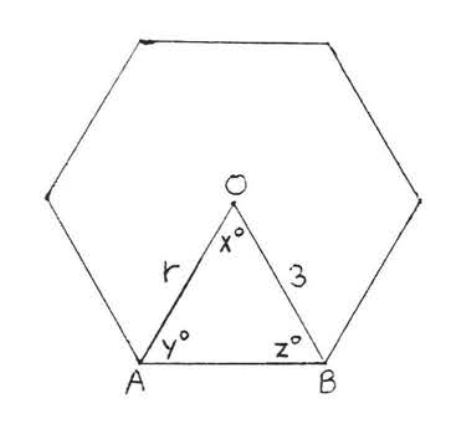
2.
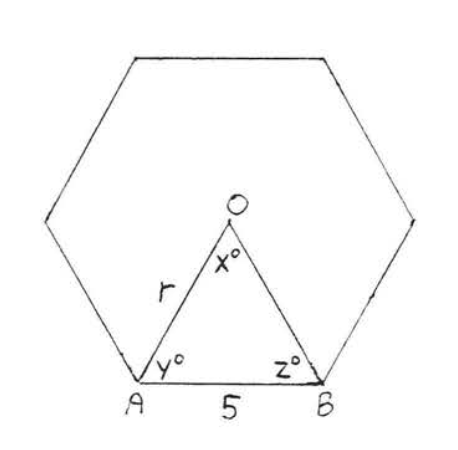
3.
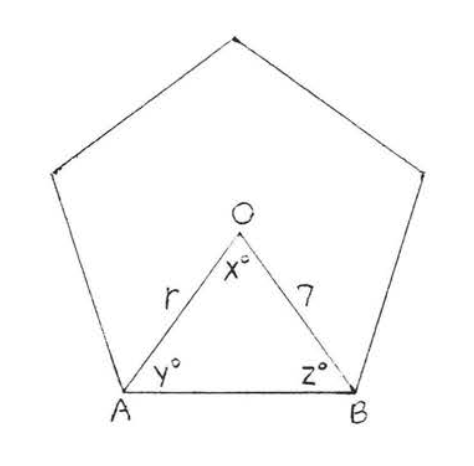
4.
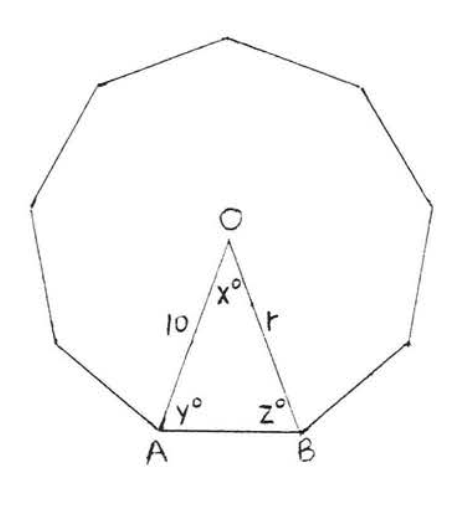
5.
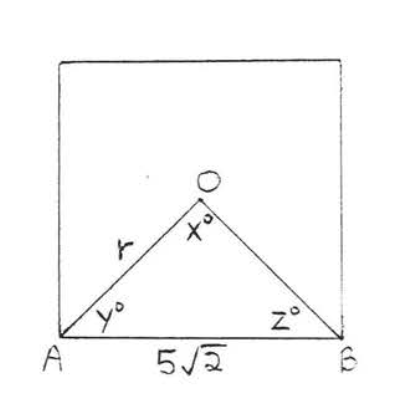
6.
7 - 18. Find the apothem, perimeter and area to the nearest tenth:
7. regular pentagon with side 40.
8. regular pentagon with side 16.
9. regular hexagon with side 20.
10. regular hexagon with side 16.
11. regular decagon (ten-sided figure) with side 20.
12. regular nonagon (nine-sided figure) with side 20.
13. regular pentagon with radius 20.
14. regular pentagon with radius 5.
15. regular hexagon with radius 10.
16. regular hexagon with radius 20.
17. regular decagon with radius 10.
18. regular nonagon with radius 20.


