7.2: Circles

The circle is one of the most frequently encountered geometric figures. Wheels, rings, phonograph records, clocks, coins are just a few examples of common objects with circular shape. The circle has many applications in the construction of machinery and in architectural and ornamental design.

To draw a circle we use an instrument called a compass (Figure $\PageIndex{1}$). The compass consists of two arms, one ending in a sharp metal point and the other attached to a pencil. We draw the circle by rotating the pencil while the metal point is held so that it does not move, The position of the metal point is called the center of the circle. The distance between the center and the tip of the pencil is called the radius of the circle, the radius remains the same as the circle is drawn.

Figure $\PageIndex{1}$: Using a compass to draw a circle.

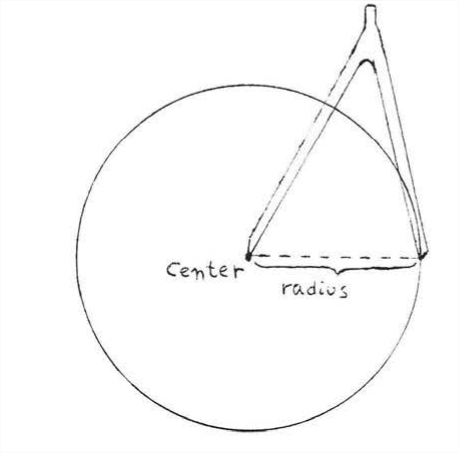
The method of constructing a circle suggests the following definition:

Definition: Circle

A circle is a figure consisting of all points which are a given distance from a fixed point called the center. For example the circle in Figure 2 consists of all points which are a distance of 3 from the center 0. The radius is the distance of any point on the circle from the center.

The circle in Figure $\PageIndex{2}$ has radius 2. The term radius is also used to denote any of the line segments from a point on the circle to the center. In Figure $\PageIndex{2}$, each of the line segments $OA, OB$, and $OC$ is a radius. It follows from the definition of circle that all radii of a circle are equal. So in Figure $\PageIndex{2}$ the three radii $OA, OB$, and $OC$ are all equal to 3.

Figure $\PageIndex{2}$: A circle with radius 3. (Copyright; author via source)

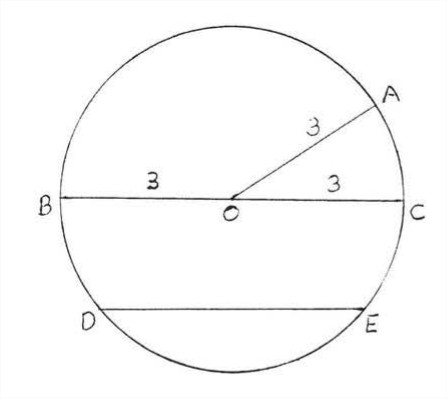
A circle is usually named for its center. The circle in Figure $\PageIndex{2}$ is called circle $O$.

A chord is a line segment joining two points on a circle. In Figure $\PageIndex{2}$, $DE$ is a chord. A diameter is a chord which passes through the center. \(BC is a diameter. A diameter is always twice the length of a radius since it consists of two radii. Any diameter of circle 0 is equal to 6. All diameters of a circle are equal.

Example $\PageIndex{1}$

Find the radius and diameter and diameter.

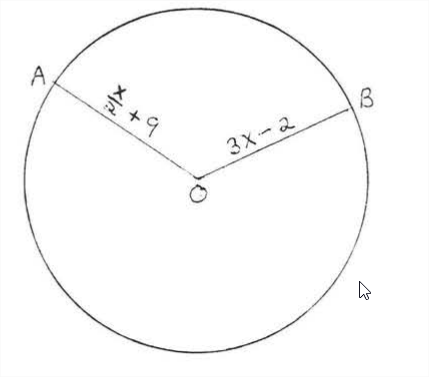
Solution

All radii are equal so

\[\begin{aligned}

O A &=O B \\

\frac{x}{2}+9 &=3 x-2 \\

(2)\left(\frac{x}{2}+9\right) &=(3 x-2)(2) \\

x+18 &=6 x-4 \\

22 &=5 x \\

x &=\frac{22}{5}=4.4

\end{aligned}\]

Check:

$OA = OB$

\[\begin{array}{r|l}

\frac{x}{2}+9 & 3 x-2 \\

\frac{4.4}{2}+9 & 3(4.4)-2 \\

2.2+9 & 13.2-2 \\

11.2 & 11.2

\end{array}\]

Therefore the radius = $OA = OB$ = 11.2 and the diameter = 2(11.2) =22.4.

Answer: radius =11.2, diameter =22.4.

The following three theorems show that a diameter of a circle and the perpendicular bisector of a chord in a circle are actually the same thing.

Theorem $\PageIndex{1}$

A diameter perpendicular to a chord bisects the chord.

In Figure $\PageIndex{3}$, if $AB \perp CD$ then $AE = EB$.

Figure $\PageIndex{3}$: The diameter $CD$ is perpendicular to chord $AB$.

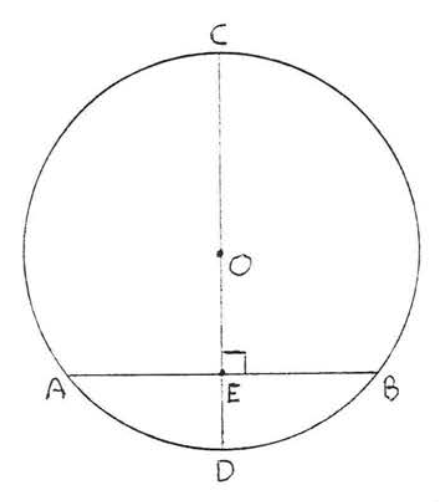
Proof

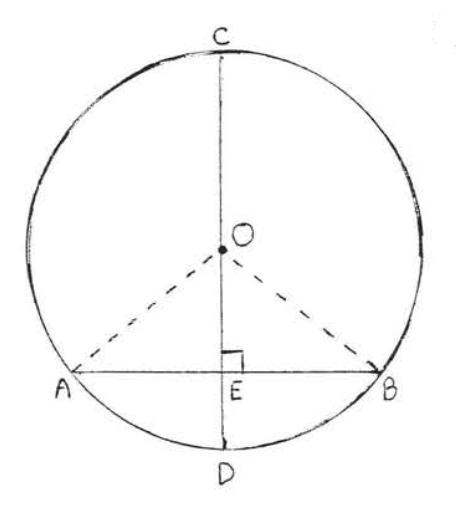
Figure $\PageIndex{4}$: Draw $OA$ and $OB$.

Draw $OA$ and $OB$ (Figure $\PageIndex{4}$). $OA = OB$ because all radii of a circle are equal. $OE = OE$ because of identity. Therefore $\triangle ACE \cong \triangle BOE$ by Hyp-Leg = Hyp-Leg. Hence $AE = BE$ because they are corresponding sides of congruent triangles.

Example $\PageIndex{2}$

Find $AB$:

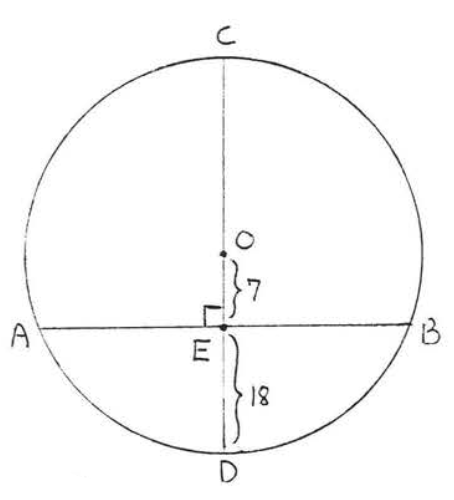
Solution

Figure $\PageIndex{5}$: Draw $OA$.

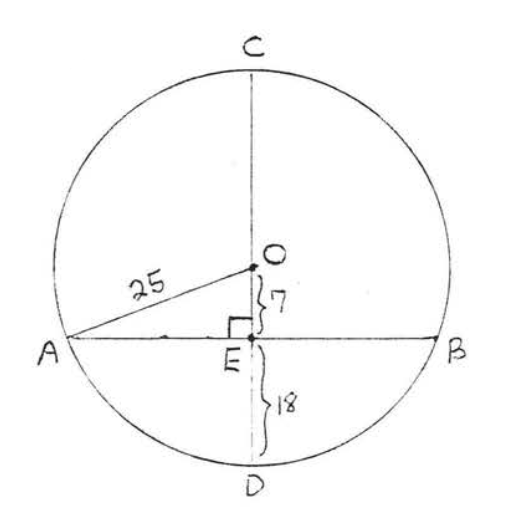
Draw $OA$ (Figure $\PageIndex{5}$). $OA = \text{radius} = OD = 18 + 7 = 25$. $\triangle AOE$ is a right triangle and therefore we can use the Pythagorean theorem to find $AE$:

$\begin{array} {rcl} {\text{AE}^2+\text{CE}^2} & = & {\text{CA}^2} \\ {\text{AE}^2 + 7^2} & = & {25^2} \\ {\text{AE}^2 + 49} & = & {625} \\ {\text{AE}^2} & = & {576} \\ {\text{AE}} & = & {24} \end{array}$

By Theorem $\PageIndex{1}$, $EB = AE = 24$ so $AB = AE + EB = 24 + 24 = 48$.

Answer: $AB = 48$.

Theorem $\PageIndex{2}$

A diameter that bisects a chord which is not a diameter is perpendicular to it.

In Figure $\PageIndex{6}$, if $AE = EB$ then $AB \perp CD$.

Figure $\PageIndex{6}$: Diameter $CD$ bisects chord $AB$.

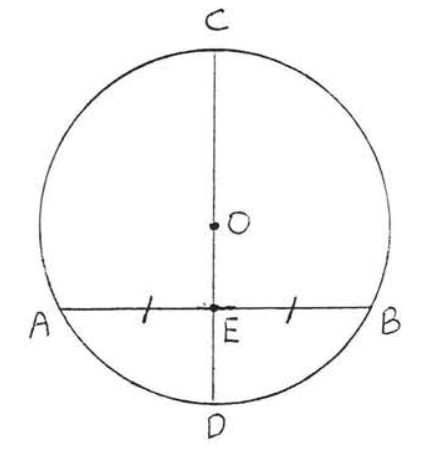
Proof

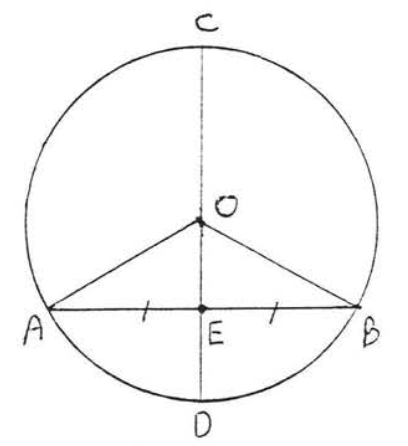
Figure $\PageIndex{7}$: Draw $OA$ and $OB$.

Draw $OA$ and $OB$ (Figure $\PageIndex{7}$). $OA = OB$ because all radii are equal, $OE = OE$ (identity) and $AE = EB$ (given). Therefore $\triangle AOE \cong \triangle BOE$ by $SSS = SSS$. Therefore $\triangle AEO = \triangle BEO$. Since $\angle AEO$ and $\angle BEO$ are also supplementary we must also have $\angle AEO = \angle BEO = 90^{\circ}$, which is what we had to prove.

Example $\PageIndex{3}$

Find $x$:

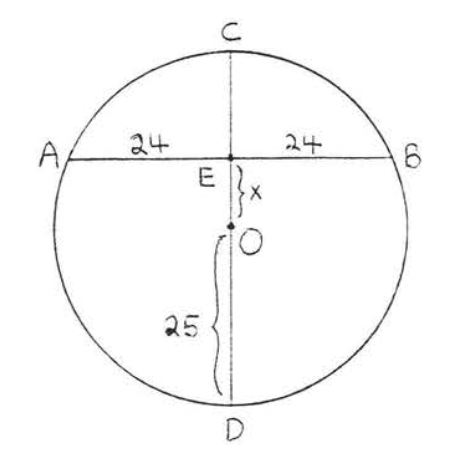
Solution

Figure $\PageIndex{8}$: Draw $OA$.

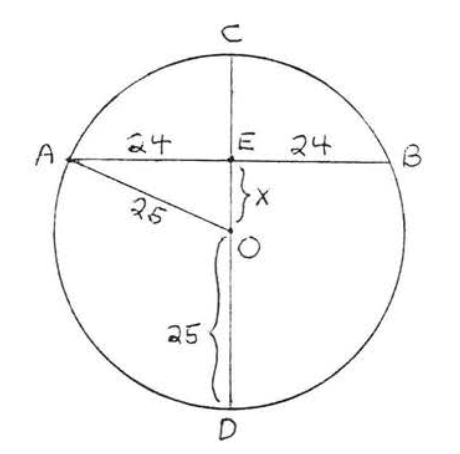
Draw $OA$ (Figure $PageIndex{8}$). $OA = \text{radius} = OD = 25$. According to Theorem $\PageIndex{2}$, $AB \perp CD$. Therefore $\triangle AOE$ is a right triangle, and we can use the Pythagorean theorem to find $x$:

$$\begin{array} {rcl} {\text{OE}^2 + \text{AE}^2} & = & {\text{OA}^2} \\ {x^2 + 24^2} & = & {25^2} \\ {x^2 + 576} & = & {625} \\ {x^2} & = & {49} \\ {x} & = & {7} \end{array}$$

Answer: $x = 7$.

Theorem $\PageIndex{3}$

The perpendicular bisector of a chord must pass through the center of the circle (that is, it is a diameter).

In Figure $\PageIndex{9}$, if $CD \perp AB$ and $AE = EB$ then $O$ must lie on $CD$.

Figure $\PageIndex{9}$: If $CD$ is a perpendicular bisector of $AB$ then $CD$ must pass through $O$.

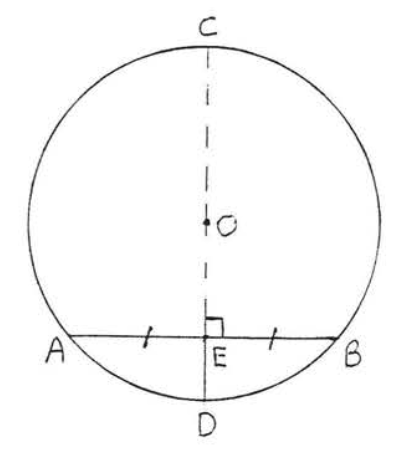
Proof

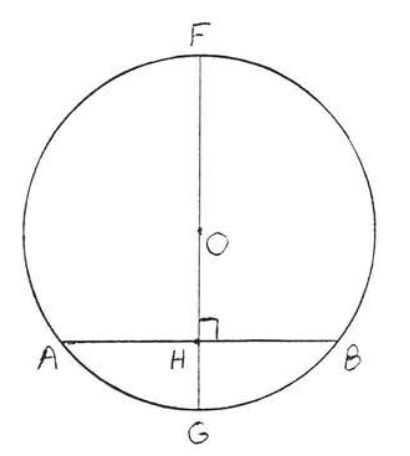
Figure $\PageIndex{10}$: Draw $FG$ through $O$ perpendicular to $AB$.

Draw a diameter $FG$ through $O$ perpendicular to $AB$ at $H$ (Figure $\PageIndex{10}$). Then according to Theorem $\PageIndex{1}$ $H$ must bisect $AB$. Hence $H$ and $E$ are the same point and $FG$ and $CD$ are the same line. So $O$ lies on $CD$. This completes the proof.

Example $\PageIndex{4}$

Find the radius of the circle:

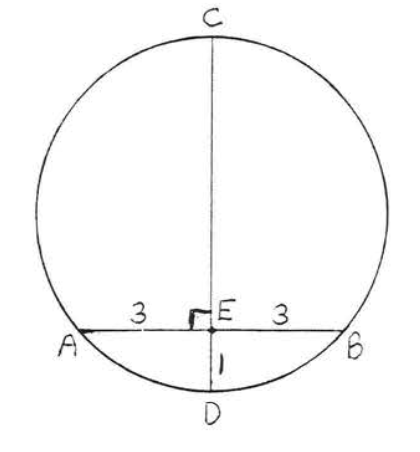
Solution

Figure $\PageIndex{11}$: Draw $OA$ and let $r$ be the radius.

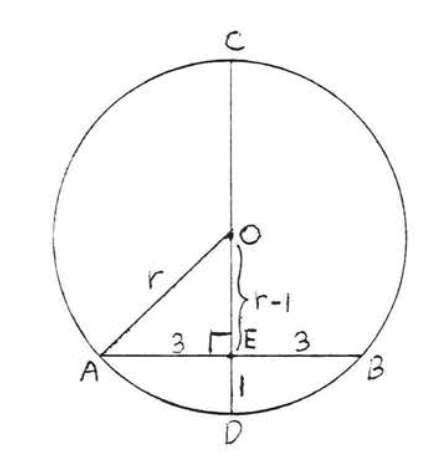
According to Theorem $\PageIndex{3}$, $O$ must lie on $CD$. Draw $OA$ (Figure $\PageIndex{11}$). Let $r$ be the radius. Then $OA = OD = r$ and $OE = r - 1$. To find $r$ we apply the Pythagorean theorem to right triangle $AOE$:

$$\begin{array} {rcl} {\text{AE}^2 + \text{OE}^2} & = & {\text{OA}^2} \\ {3^2 + (r - 1)^2} & = & {r^2} \\ {9 + r^2 - 2r + 1} & = & {r^2} \\ {10} & = & {2r} \\ {5} & = & {r} \end{array}$$

Answer: $r = 5$.

Example $\PageIndex{5}$

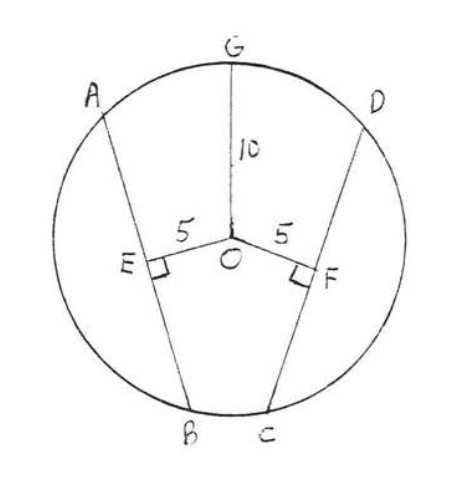
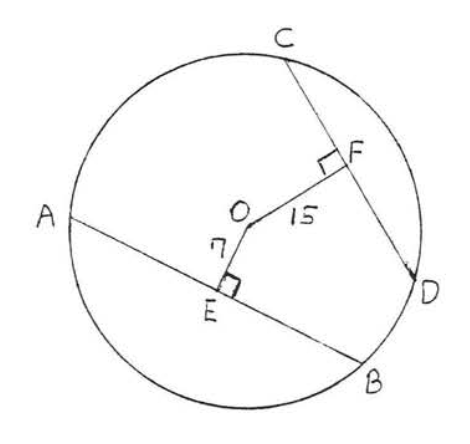
Find which chord, $AB$ or $CD$, is larger if the radius of the circle is 25:

Solution

Figure $\PageIndex{12}$: Draw $OA, OB, OC$ and $OD$.

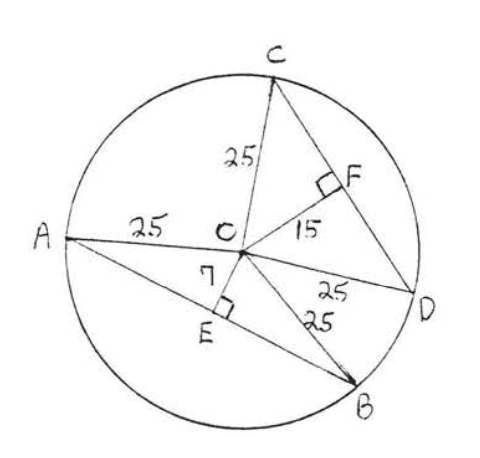
Draw $OA, OB, OC$ and $OD$ (Figure $\PageIndex{12}$). Each is a radius and equal to 25. We use the Pythagorean theorem, applied to right triangle $AOE$, to find $AE$:

$$\begin{array} {rcl} {\text{AE}^2 + \text{OE}^2} & = & {\text{OA}^2} \\ {\text{AE}^2 + 7^2} & = & {25^2} \\ {\text{AE}^2 + 49} & = & {625} \\ {\text{AE}^2} & = & {576} \\ {\text{AE}} & = & {24} \end{array}$$

Since perpendicular $OE$ bisects $AB$ (Theorem $\PageIndex{1}$) $BE = AE = 24$ and so $AB = AE + BE = 24 + 24 = 48$.

Similarly, to find $CF$, we apply the Pythagorean theorem to right triangle $COF$:

$$\begin{array} {rcl} {\text{CF}^2 + \text{OF}^2} & = & {\text{OC}^2} \\ {\text{CF}^2 + 15^2} & = & {25^2} \\ {\text{CF}^2 + 225} & = & {625} \\ {\text{CF}^2} & = & {400} \\ {\text{CF}} & = & {20} \end{array}$$

Again, from Theorem $\PageIndex{1}$, we know $OF$ bisects $CD$, hence $DF = CF = 20$ and $CD = 40$.

Answer: $AB = 48$, $CD = 40$, $AB$ is larger than $CD$.

Example $\PageIndex{5}$ suggests the following Theorem (which we state without proof):

Theorem $\PageIndex{4}$

The length of a chord is determined by its distance from the center of the circle; the closer to the center, the larger the chord.

Historical Note

The definition of a circle and essentially all of the theorems of this and the next two sections can be found in Book III of Euclid's Elements.

Problems

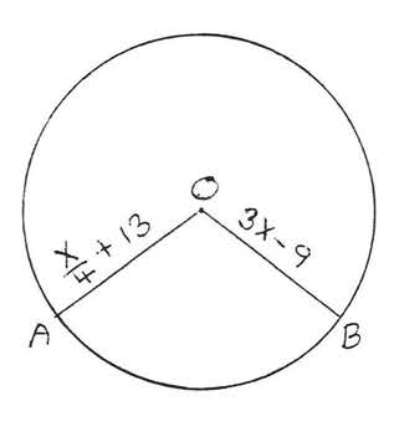
1 - 2. Find the radius and diameter:

1.

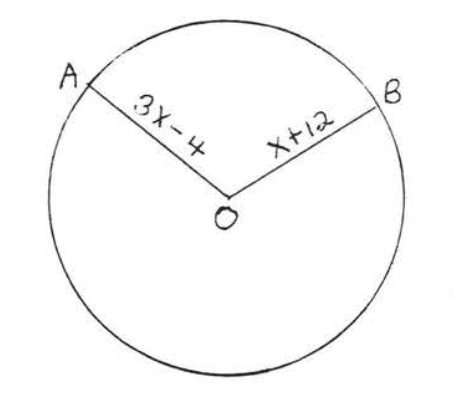
2.

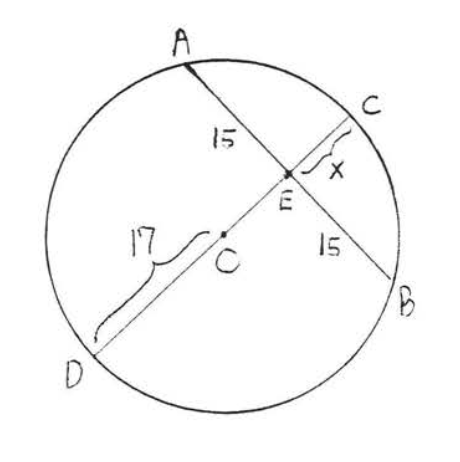
3 - 4. Find $AB$:

3.

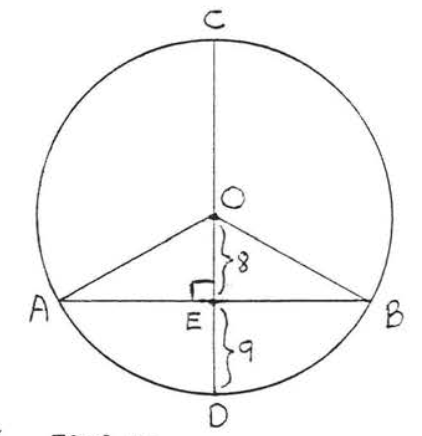
4.

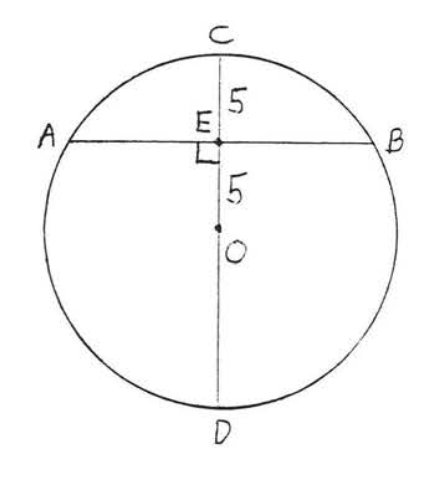
5 - 6. Find $x$:

5.

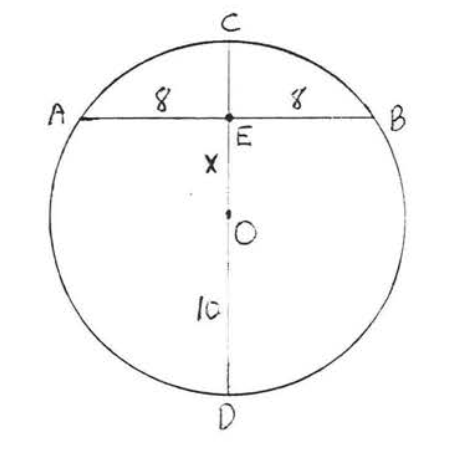
6.

7 - 10. Find the radius and diameter:

7.

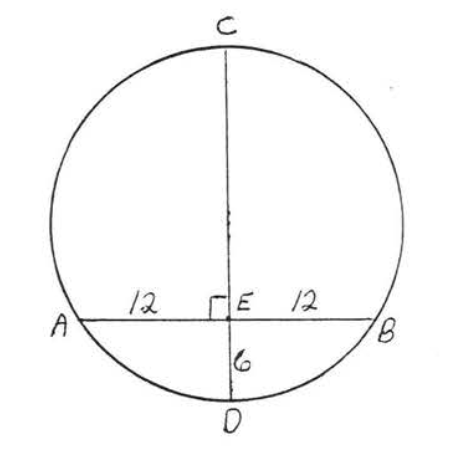
8.

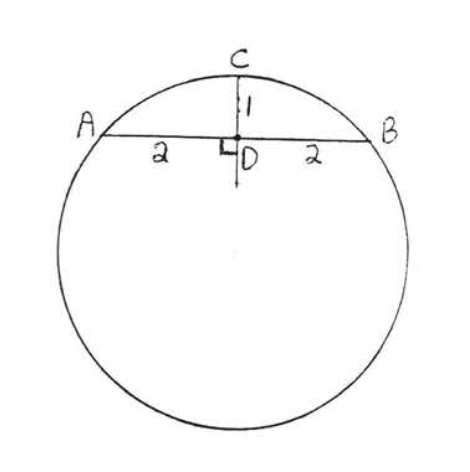
9.

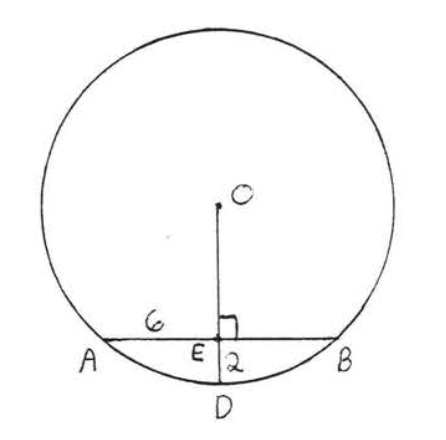
10.

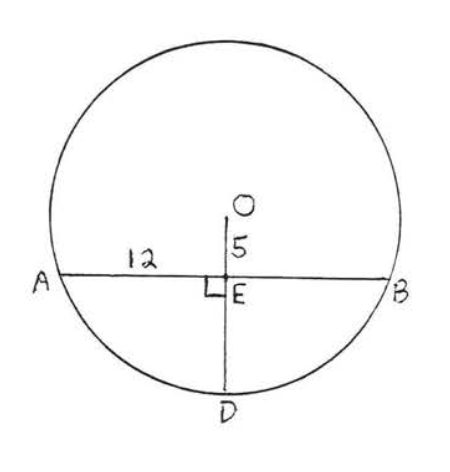
11 - 12. Find the lengths of $AB$ and $CD$:

11.

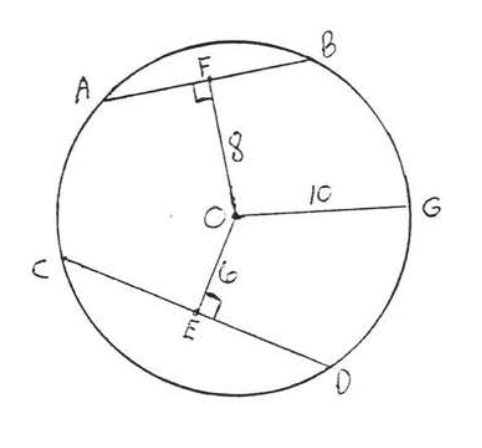
12.