7.3: Tangents to the Circle

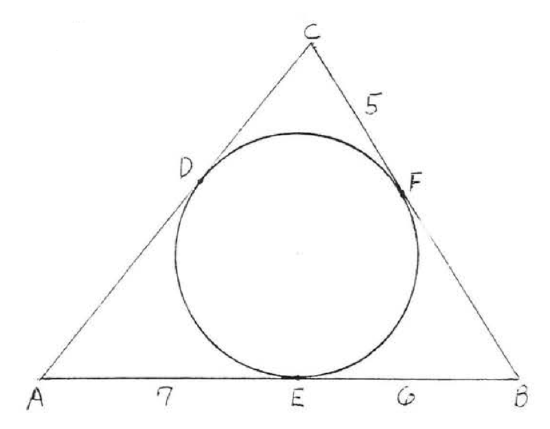
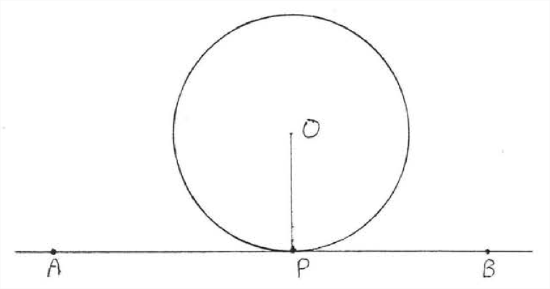
A tangent to a circle is a line which intersects the circle in exactly one point. In Figure 1 line $\overleftrightarrow{AB}$ is a tangent, intersecting circle $O$ just at point $P$.

Figure 1. $\overleftrightarrow{AB}$ is tangent to circle $O$ at point $P$.

A tangent has the following important property:

Theorem $\PageIndex{1}$

A tangent is perpendicular to the radius drawn to the point of intersection.

Proof

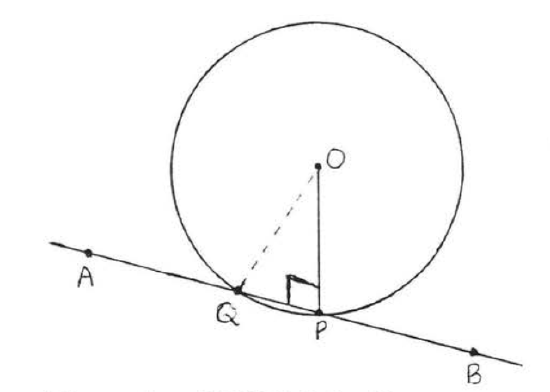
$OP$ is the shortest line segment that can be drawn from 0 to line $\overleftrightarrow{AB}$. This is because if $Q$ were another point on $\overleftrightarrow{AB}$ then $OQ$ would be longer than radius $OR = OP$ (Figure $\PageIndex{2}$). Therefore $OP \perp \overleftrightarrow{AB}$ since the shortest line segment that can be drawn from a point to a straight line is the perpendicular (Theorem $\PageIndex{2}$, section 4.6). This completes the proof.

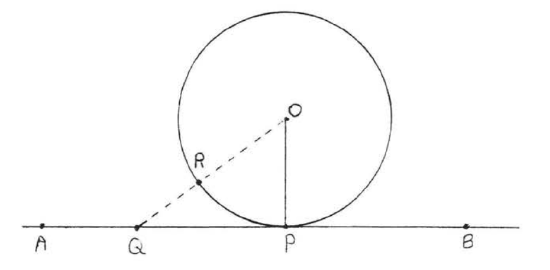
Figure $\PageIndex{2}$: $OP$ is the shortest line segment that can be drawn from $O$ to line $\overleftrightarrow{AB}$.

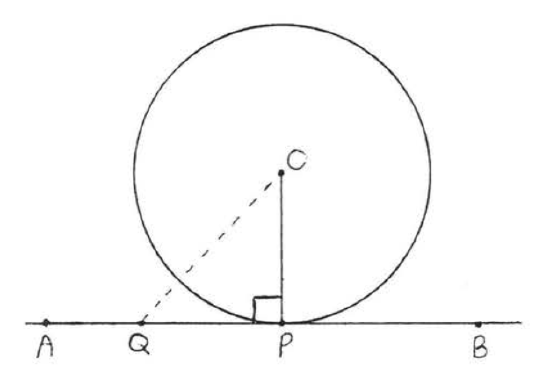
In Figure $\PageIndex{1}$ tangent $\overleftrightarrow{AB}$ is perpendicular to radius $OP$ at the point of intersection $P$.

Example $\PageIndex{1}$

Find $x$:

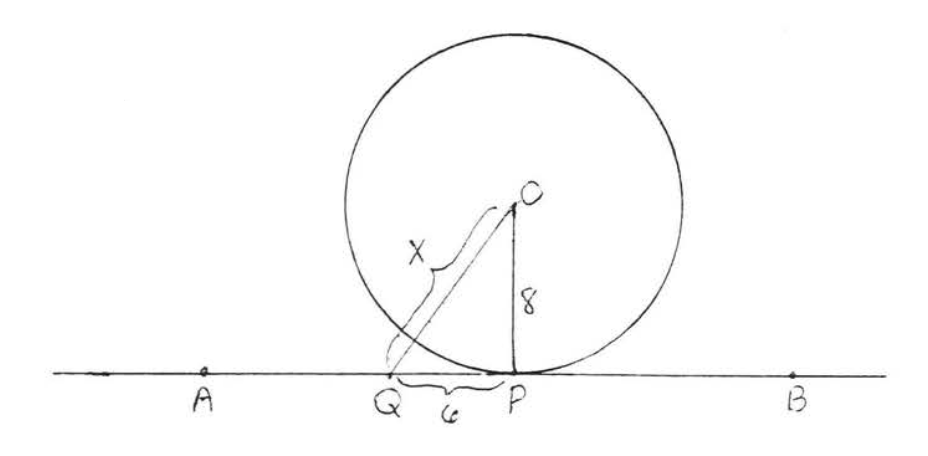
Solution

According to Theorem $\PageIndex{1}$, $\angle QPO$ is a right angle. We may therefore apply the Pythagorean theorem to right triangle $QPO$:

$$\begin{array} {rcl} {6^2 + 8^2} & = & {x^2} \\ {36 + 64} & = & {x^2} \\ {100} & = & {x^2} \\ {10} & = & {x} \end{array}$$

Answer: $x = 10$.

The converse of Theorem $\PageIndex{1}$ is also true:

Theorem $\PageIndex{2}$

A line perpendicular to a radius at a point touching the circle must be a tangent.

In Figure $\PageIndex{3}$, if $OP \perp \overleftrightarrow{AB}$ then $\overleftrightarrow{AB}$ must be a tangent; that is, $P$ is the only point at which $\overleftrightarrow{AB}$ can touch the circle (Figure $\PageIndex{4}$).

Figure $\PageIndex{3}$: If $OP \perp \overleftrightarrow{AB}$ then $\overleftrightarrow{AB}$ must be a tangent.

Figure $\PageIndex{4}$: Theorem $\PageIndex{2}$ implies that this cannot happen.

Proof

Suppose $Q$ were some other point on $\overleftrightarrow{AB}$. Then $OQ$ is the hypotenuse of right triangle $OPQ$ (see Figure $\PageIndex{3}$). According to Theorem $\PageIndex{1}$, section 4.6, the hypotenuse of a right triangle is always larger than a leg. Therefore hypotenuse $OQ$ is larger than leg $OP$. Since $OQ$ is larger than the radius $OP$, $Q$ cannot be on the circle. We have shown that no other point on $AB$ besides $P$ can be on the circle. Therefore $\overleftrightarrow{AB}$ is a tangent. This completes the proof.

Example $\PageIndex{2}$

Find $x$, $\angle O$, and $\angle P$:

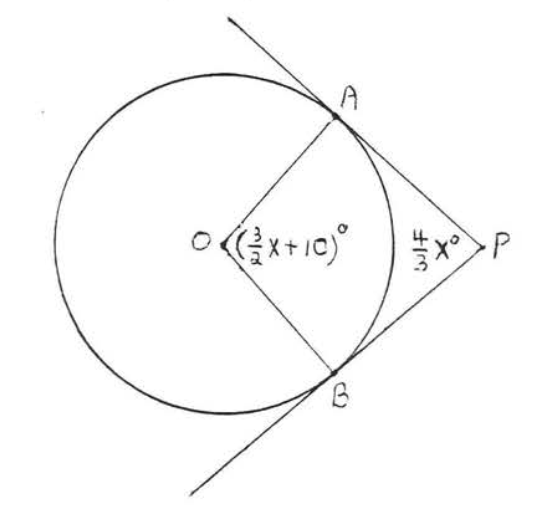
Solution

$\overleftrightarrow{AP}$ and $\overleftrightarrow{BP}$ are tangent to circle $O$, so by Theorem $\PageIndex{1}$, $\angle OAP = \angle OBP = 90^{\circ}$. The sum of the angles of quadrilateral $AOBP$ is $360^{\circ}$ (see Example 1.5.5, section 1.5), hence

$$\begin{array} {rcl} {90 + \left(\dfrac{3}{2} x + 10\right) + 90 + \dfrac{4}{3} x} & = & {360} \\ {\dfrac{3}{2}x + \dfrac{4}{3} x + 190} & = & {360} \\ {\dfrac{3}{2} x + \dfrac{4}{3} x} & = & {170} \\ {(6)\left(\dfrac{3}{2}x\right) + (6)\left(\dfrac{4}{3} x\right)} & = & {(6)(170)} \\ {9x + 8x} & = & {1020} \\ {17x} & = & {1020} \\ {x} & = & {60} \end{array}$$

Substituting 60 for $x$, we find

$\angle O = \left(\dfrac{3}{2}x + 10\right)^{\circ} = \left(\dfrac{3}{2}(60) + 10\right)^{\circ} = (90 + 10)^{\circ} = 100^{\circ}$

and

$\angle P = \dfrac{4}{3} x^{\circ} = \dfrac{4}{3} (60)^{\circ} = 80^{\circ}$.

Check:

$\angle A + \angle O + \angle B + \angle P = 90^{\circ} + 100^{\circ} + 90^{\circ} + 80^{\circ} = 360^{\circ}.$

Answer

$x = 60, \angle O = 100^{\circ}, \angle P = 80^{\circ}$.

If we measure line segments $AP$ and $BP$ in Example $\PageIndex{2}$ we will find that they are approximately equal in length. In fact we can prove that they must be exactly equal:

Theorem $\PageIndex{3}$

Tangents drawn to a circle from an outside point are equal.

In Figure $\PageIndex{5}$ if $\overleftrightarrow{AP}$ and $\overleftrightarrow{BP}$ are tangents then $AP = BP$.

Figure $\PageIndex{5}$: If $\overleftrightarrow{AP}$ and $\overleftrightarrow{BP}$ are tangents then $AP = BP$.

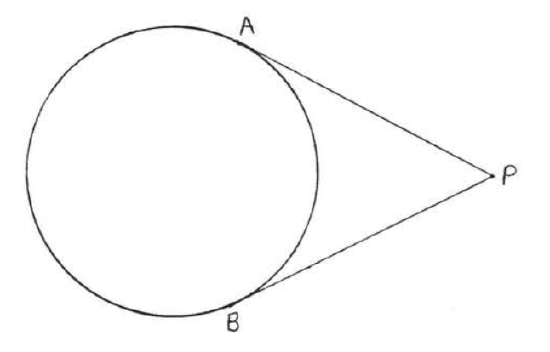
Proof

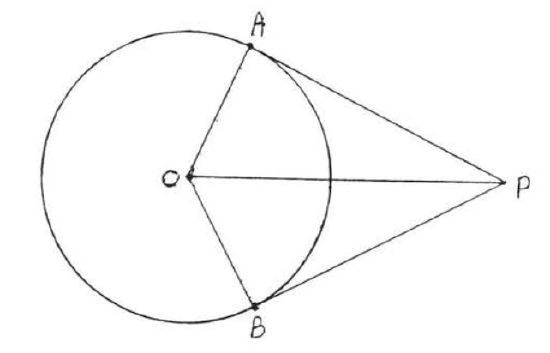
Figure $\PageIndex{6}$: Draw $OA, OB$ and $OP$.

Draw $OA, OB$, and $OP$ (Figure $\PageIndex{6}$). $OA = OB$ (all radii are equal), $OP = OP$ (identity) and $\angle A = \angle B = 90^{\circ}$ (Theorem (\PageIndex{1}\)), hence $\triangle AOP \cong \triangle BOP$ by Hyp-Leg = Hyp-Leg. Therefore $AP = BP$ beause they are corresponding sides of congruent triangles.

Example $\PageIndex{3}$

Find $x$ and $y$:

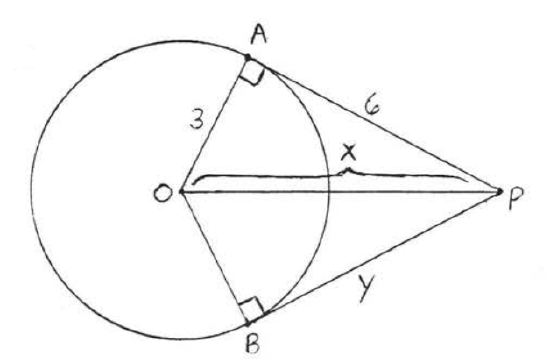
Solution

By the Pythagorean theorem, $x^2 = 3^2 + 6^2 = 9 + 36 = 45$ and $x = \sqrt{45} = \sqrt{9}\sqrt{5} = 3\sqrt{5}$. By Theorem $\PageIndex{3}$, $y = BP = AP = 6$.

Answer: $x = 3\sqrt{5}, y = 6$.

Example $\PageIndex{4}$

Find $x$:

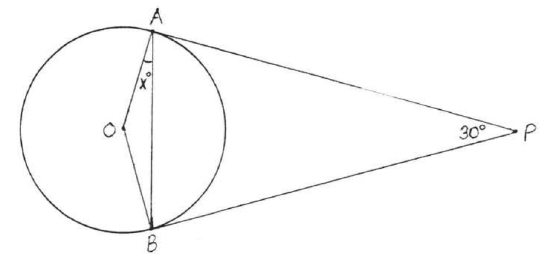
Solution

By Theorem $\PageIndex{3}$, $AP = BP$. So $\triangle ABP$ is isosceles with $\angle PAB = \angle PBA = 75^{\circ}$. Therefore $x^{\circ} = 90^{\circ} - 75^{\circ} = 15^{\circ}$.

Answer: $x = 15$.

If each side of a polygon is tangent to a circle, the circle is said to be inscribed in the polygon and the polygon is said to be circumscribed about the circle. In Figure $\PageIndex{7}$ circle 0 is inscribed in quadrilateral $ABCD$ and $ABCD$ is circumscribed about circle $O$.

Figure $\PageIndex{7}$: Circle $O$ is inscribed in $ABCD$.

Example $\PageIndex{5}$

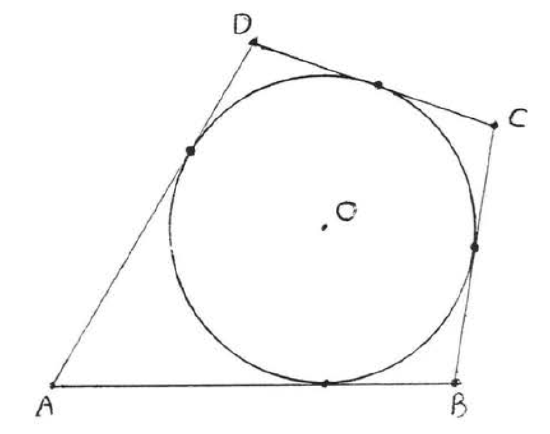
Find the perimeter of $ABCD$:

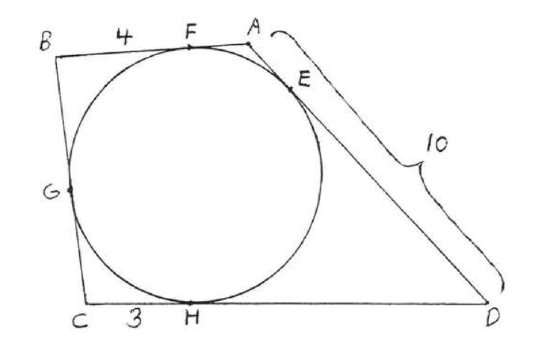
Solution

By Theorem $\PageIndex{3}$, $CG = CH = 3$ and $BG = BF = 4$. Also $DH = DE$ and $AF = AE$ so $DH + AF = DE + AE =10$.

Therefore the perimeter of $ABCD = 3 + 3 + 4 + 4 + 10 + 10 = 34.$

Answer: $P = 34$.

Problems

1 - 4. Find $x$:

1.

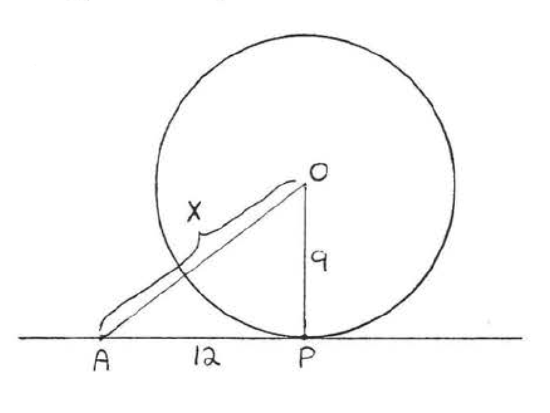
2.

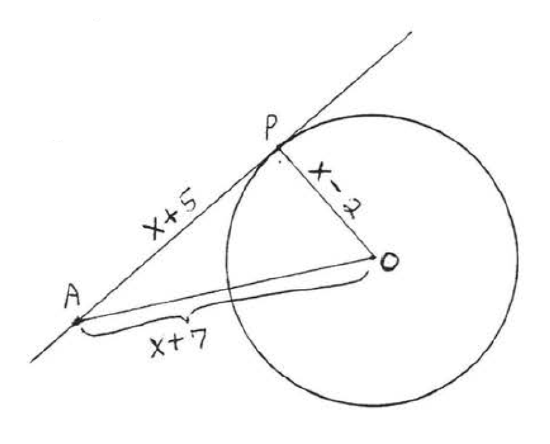
3.

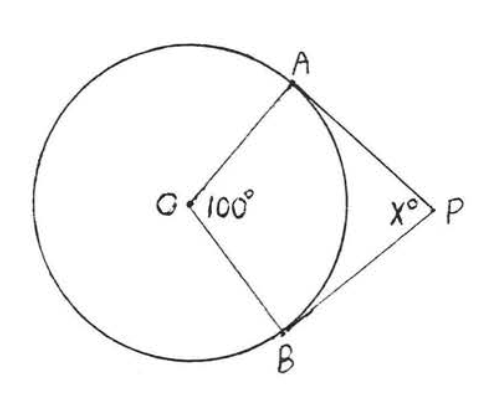
4.

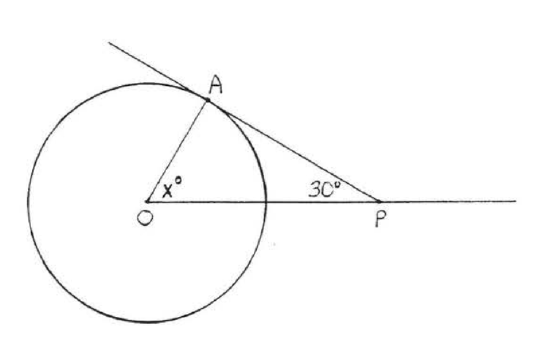
5 - 6. Find $x$, $\angle O$ and $\angle P$:

5.

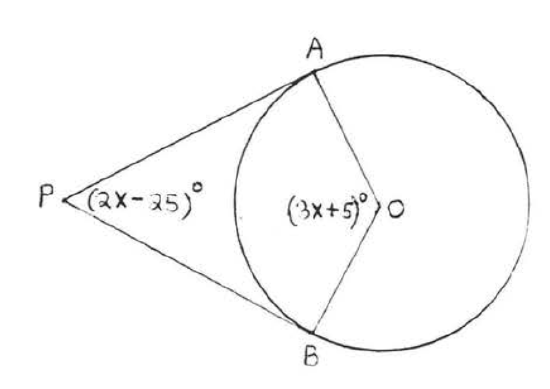
6.

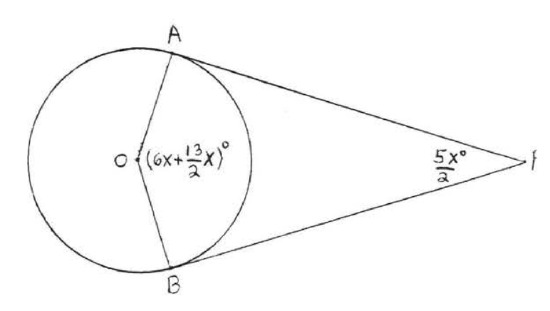
7 - 8. Find $x$ and $y$:

7.

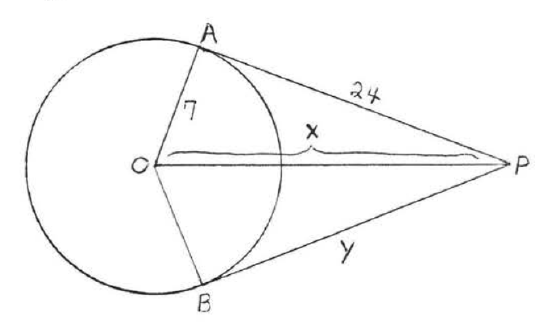
8.

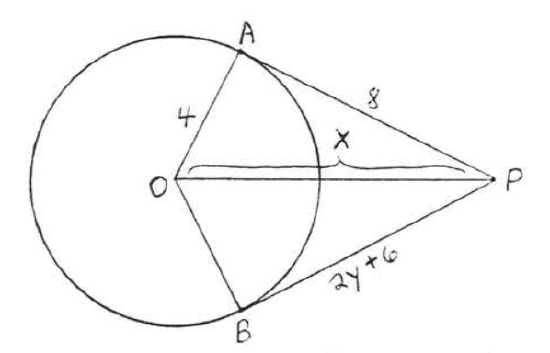
9 - 12. Find $x$:

9.

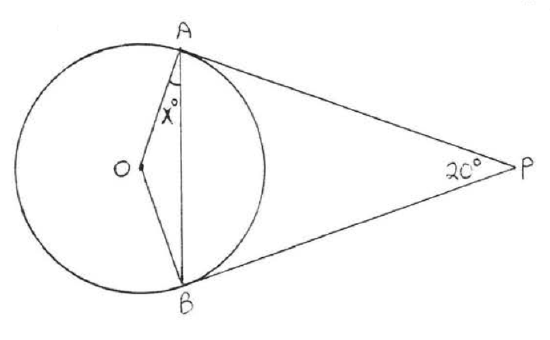
10.

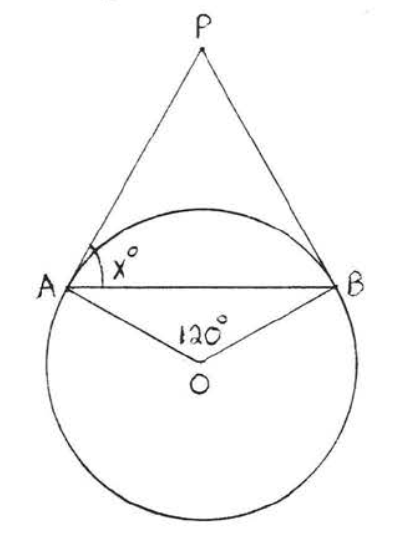
11.

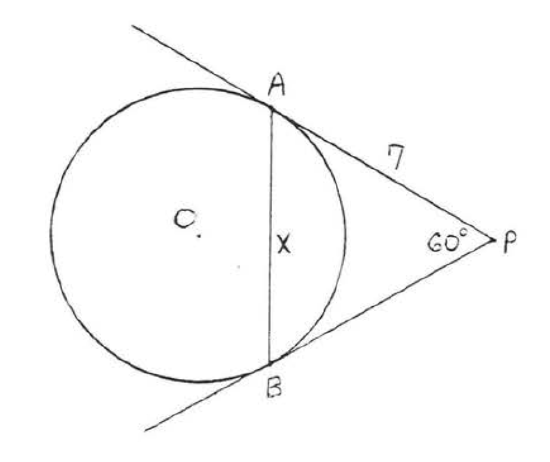
12.

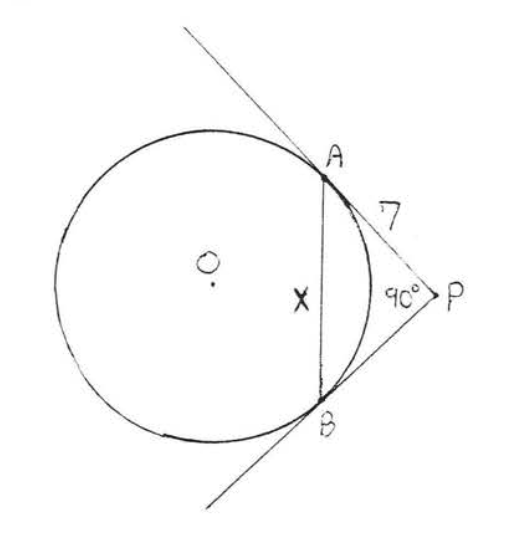
13 - 16. Find the perimeter of the polygon:

13.

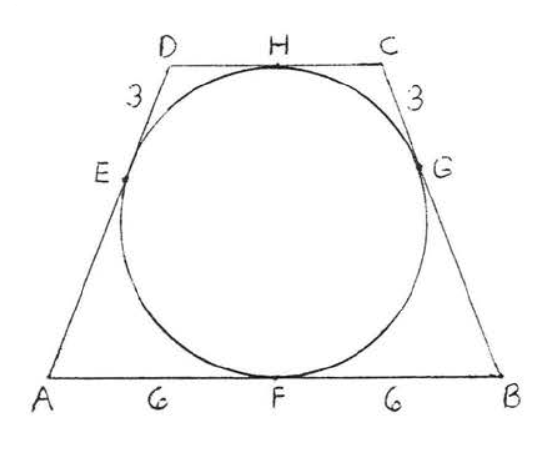
14.

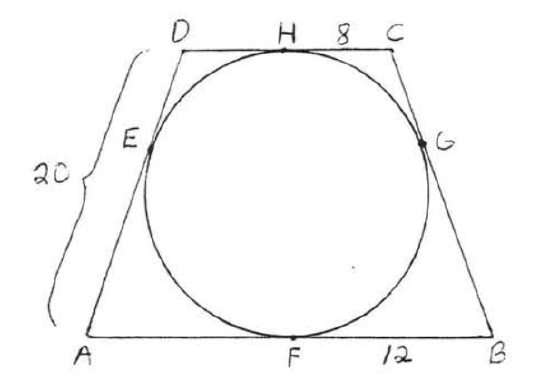
15.

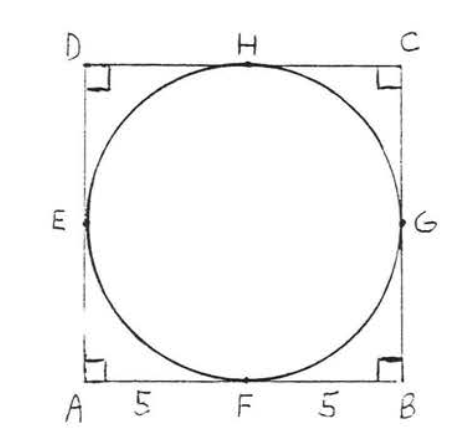
16.