7.4: Degrees in an Arc

Last updated
Save as PDF

Page ID: 34155

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

An arc is a part of the circle included between two points. The symbol for the are included between points $A$ and $B$ Is $\widehat{AB}$. In Figure $\PageIndex{1}$ there are two arcs determined by $A$ and $B$. The shorter one is called the minor arc and the longer one is called the major arc. Unless otherwise indicated, $\widehat{AB}$ will always refer to the minor arc. In $\PageIndex{1}$, we might also write $\widehat{ACB}$ instead of $\widehat{AB}$ to intercept the major arc.

Figure $\PageIndex{1}$: There are two arcs determined by $A$ and $B$, the minor are and the major arc.

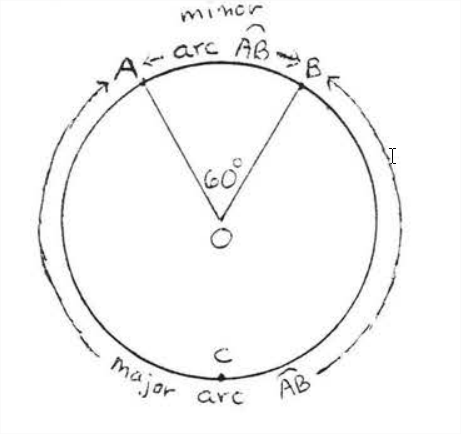
A central angle is an angle vertex is the center of the circle and whose sides are radii. In Figure $\PageIndex{1}$, $\angle AOB$ is a central angle. $\angle AOB$ is said to intercept arc $\widehat{AB}$.

The number of degrees in an arc is defined to be the number of degrees in the central angle that intercepts the arc. In Figure 1 minor are $\widehat{AB}$ has $60^{\circ}$ because $\angle AO 3=60^{\circ}$, we write $\widehat{AB} \stackrel{\circ}{=} 60^{\circ},$ where the symbol $\stackrel{\circ}{=}$ means equal in degrees. The plain $=$ symbol will be reserved for arc length, to be discussed in Section 7.5.

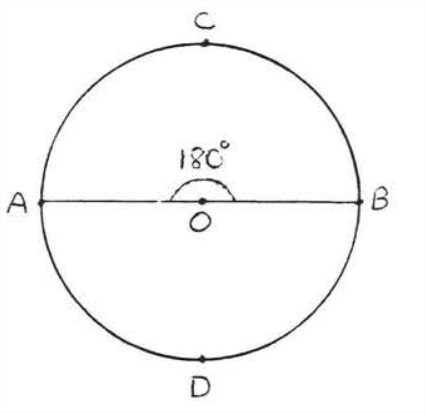
In Figure 2 $\angle AOB$ is a straight angle so $\angle AOB=180^{\circ}$ and $\widehat{ACB} \stackrel{\circ}{=} 180^{\circ} .$ Similarly $\widehat{ADB} \stackrel{\circ}{=} 180^{\circ}$. Each of these arcs is called a semicircle. The complete circle measures $360^{\circ} $.

Figure 2: $\angle AOB=180^{\circ}$ and $\widehat{ACB} \stackrel{\circ}{=} 180^{\circ}$

Example $\PageIndex{1}$

Find the number of degrees in arcs $\widehat{AB}$ and $\widehat{ACB}$:

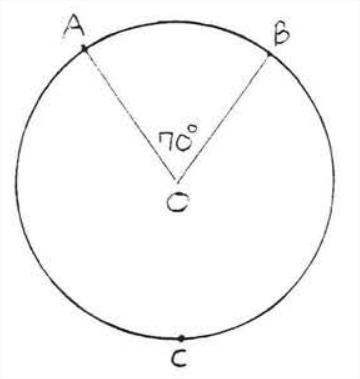
$clipboard_e0d7ebadc7b384913fc1c18a4cd44985c.png$

Solution

$\widehat{A B} \stackrel{\circ}{=} \angle A C B=\angle A C B=70^{\circ}$ and $ \widehat{A C B} \stackrel{\circ}{=} 360^{\circ}-\widehat{A B} \stackrel{\circ}{=} 360^{\circ}-70^{\circ}=290^{\circ} .$

Answer: $\widehat{A B} \stackrel{\circ}{=} 70^{\circ}, \widehat{A C B} \stackrel{\circ}{=} 290^{\circ}$

Example $\PageIndex{1}$

Find $x, y$ and $z$:

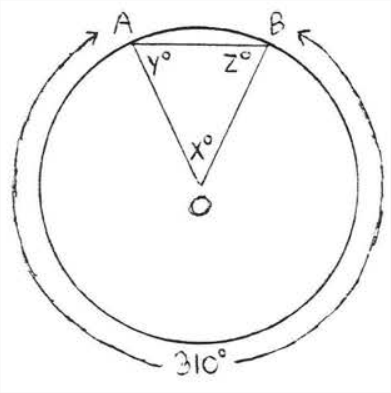
$clipboard_e06ac34d103abfbb175be70ee3a90a872.png$

Solution

$x^{\circ} \stackrel{\circ}{=} \widehat{A B} \stackrel{\circ}{=} 360^{\circ}-310^{\circ}=50^{\circ}, O A=O B$ since all radii are equal. Therefore $\triangle AOB$ is isosceles with $y^{\circ}=z^{\circ} .$ We have

\[\begin{array} {rcl} {x^{\circ} + y^{\circ} + z^{\circ}} & = & {180^{\circ}} \\ {50^{\circ} + y^{\circ} + y^{\circ}} & = & {180^{\circ}} \\ {2y^{\circ}} & = & {130^{\circ}} \\ {y^{\circ}} & = & {65^{\circ}} \end{array}\]

Answer: $x = 50, y = z = 65$.

An inscribed angle is an angle whose vertex is on a circle and whose stáes are chords of the circle. In Figure $\PageIndex{3}$, $\angle ABC$ is an inscribed angle. $\angle ABC$ is said to intercept are $\widehat{AC}$

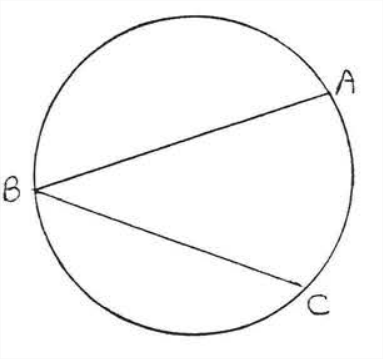
$clipboard_edc75a822369bf6b6c9a6cebcd3f90ac0.png$

FIgure $\PageIndex{3}$: $\angle ABC$ is an inscribed angle.

We shall prove the following theorem:

Theorem $\PageIndex{1}$

An inscribed angle $\stackrel{\circ}{=} \dfrac{1}{2}$ of its intercepted arc.

In Figure $\PageIndex{3}, \angle A B C \stackrel{\circ}{=} \dfrac{1}{2} \widehat{A C}$

Example $\PageIndex{3}$

Find the number of degrees in $\widehat{AC}$:

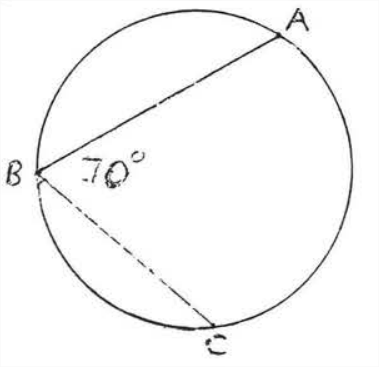
$clipboard_ebdc2277c1d0652f02bbbb37efc80ae21.png$

Solution: $\angle ABC=70^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC} .$ Therefore $\widehat{AC} \stackrel{\circ}{=} 140^{\circ}$

Answer: $\widehat{A C} \stackrel{\circ}{=} 140^{\circ}$

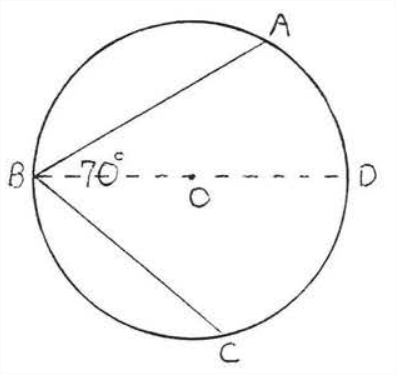
Before giving the proof of Theorem $\PageIndex{1}$ let us see if we can prove the answer to EXAMPLE $\PageIndex{3}$. Draw the diameter from $B$ through center $O$ (Figure $\PageIndex{4}$). $\angle A B C$ is divided by the diameter into two smaller angles, $\angle A B D$ and $\angle D B C$, whose sum is $70^{\circ}$. Suppose $\angle ABD = 30^{\circ}$ and $\angle DBC = 40^{\circ}$ (Figure $\PageIndex{5}$). $AO = BO$ because all radii are equal. Hence $\triangle AOB$ is isosceles with $\angle A=\angle ABD=30^{\circ}$ Similarily $\angle C=\angle DBC=40^{\circ}$. $\angle AOD$ is an exterior angle of $\triangle AOB$ and so is equal to the sum of the remote interior angles, $30^{\circ} + 30^{\circ} = 60^{\circ}$ (Theorem 1.5.2 section 1.5). Similarly $\angle COD = 40^{\circ} + 40^{\circ} = 80^{\circ}$. Therefore central angle $\angle AOC = 60^{\circ} + 80^{\circ} = 140^{\circ}$ and arc $\widehat{AC} \stackrel{\circ}{=} 140^{\circ}$. This agrees with our answer to Example $\PageIndex{3}$.

We will now give a formal proof of Theorem $\PageIndex{1}$, which will hold for any inscribed angle:

Proof of Theorem $\PageIndex{1}$: There are three cases according to whether the center is on, inside, or outside the inscribed angle (Figures $\PageIndex{6}$,$\PageIndex{7}$ and $\PageIndex{8}$).

Figure $\PageIndex{4}$: Draw diameter $BD$.

Figure $\PageIndex{5}$: Suppose $\angle A B D=30^{\circ}$ and $\angle DBC=40^{\circ}$

Figure $\PageIndex{6}$: The center is on the inscribed angle.

Figure $\PageIndex{7}$: The center is inside the inscribed angle.

Figure $\PageIndex{8}$: The center is outside the inscribed angle.

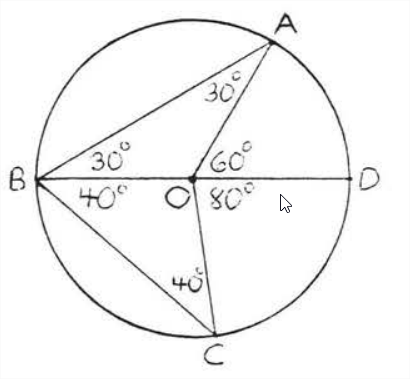
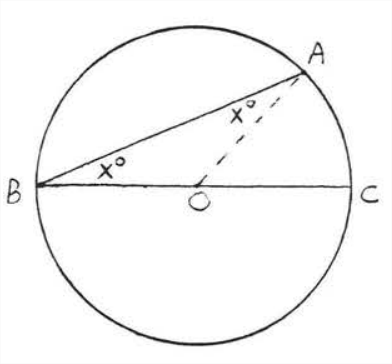
Case I. The center is on the inscribed angIe (Figure $\PageIndex{6}$). Draw $AO$. The radit are equal so $AO = BO$ and $\angle A=\angle B=x^{\circ} .$ Therefore $\widehat{AC} \stackrel{\circ}{=} \angle AOC=x^{\circ}+x^{\circ}=2 x^{\circ}$ and $\angle A B C=x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}$.

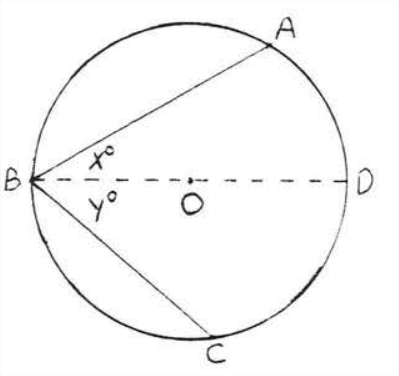
Case II. The center is inside the inscribed angle (Figure $\PageIndex{7}$). Draw diameter $BD$ from $B$ through $O$. From case I we know $\angle A B D=x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AD}$ and $\angle DBC=y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{DC} .$ Hence \[\angle ABC=x^{\circ}+y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AD}+\dfrac{1}{2} \widehat{DC} \stackrel{\circ}{=} \dfrac{1}{2}(\widehat{AD}+\widehat{DC}) \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}\]

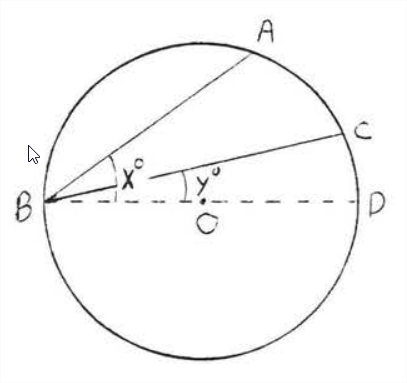
Case III. The center is outside the inscribed angle (Figure $\PageIndex{8}$). Draw diameter $BD$ from $B$ through $O$. From case I we know $\angle A B D=x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AD}$ and $\angle CBD=y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CD}$. Therefore \[ \angle ABC=x^{\circ}-y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \hat{AD}-\dfrac{1}{2} \widehat{CD} \stackrel{\circ}{=}\dfrac{1}{2}(\widehat{AD}-\widehat{CD}) \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}\]

Example $\PageIndex{4}$

Find $x$:

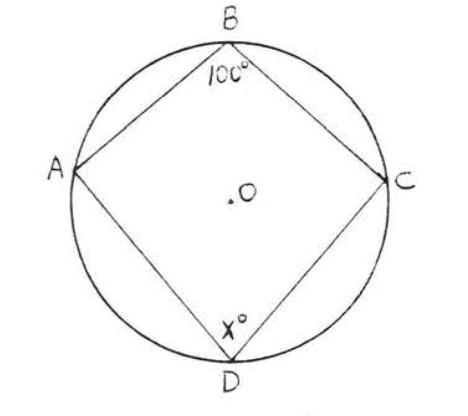
$Screen Shot 2020-12-30 at 11.37.58 AM.png$

Solution

$\angle B = 100^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{ADC}$. Therefore $\widehat{ADC} = 200^{\circ}$. So $\widehat{ABC} \stackrel{\circ}{=} 360^{\circ} - 200^{\circ} = 160^{\circ}$ and $x^{\circ} = \dfrac{1}{2} \widehat{ABC} = \dfrac{1}{2} (160^{\circ}) = 80^{\circ}$.

Answer: $x = 80$.

Example $\PageIndex{5}$

Find $x$:

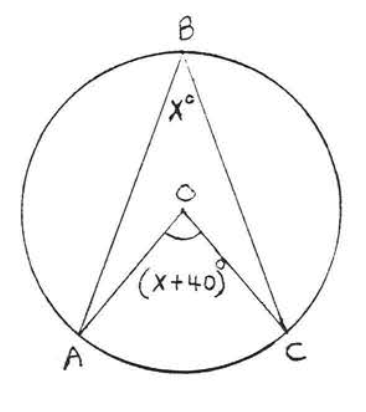
$Screen Shot 2020-12-30 at 11.44.55 AM.png$

Solution

$\angle B = x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}$. Also $\widehat{AC} \stackrel{\circ}{=} \angle AOC = (x + 40)^{\circ}$. We have

\[\begin{array} {rcl} {\angle B} & \stackrel{\circ}{=} & {\dfrac{1}{2} \widehat{AC}} \\ {x} & = & {\dfrac{1}{2} (x + 40)} \\ {2x} & = & {x + 40} \\ {x} & = & {40} \end{array}\]

Check:

$\angle B \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}$

\[\begin{array} {r|l} {x^{\circ}} & {\dfrac{1}{2} (x + 40)^{\circ}} \\ {40^{\circ}} & {\dfrac{1}{2} (40^{\circ} + 40^{\circ})^{\circ}} \\ {} & {\dfrac{1}{2} (80)^{\circ}} \\ {} & {40^{\circ}} \end{array}\]

Answer: $x = 40$.

Example $\PageIndex{6}$

Find $x$:

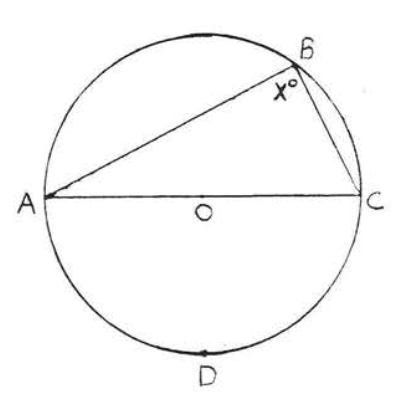
$Screen Shot 2020-12-30 at 11.59.56 AM.png$

Solution

$\widehat{ADC}$ is a semicircle so $\widehat{ADC} \stackrel{\circ}{=} 180^{\circ}$. $\angle B = x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{ADC} \stackrel{\circ}{=} \dfrac{1}{2} (180^{\circ}) = 90^{\circ}$.

Answer: $x = 90$.

We state the result of Example $\PageIndex{6}$ as a theorem:

Theorem $\PageIndex{2}$

An angle inscribed in a semicircle is a right angle.

Example $\PageIndex{7}$

Find $x$:

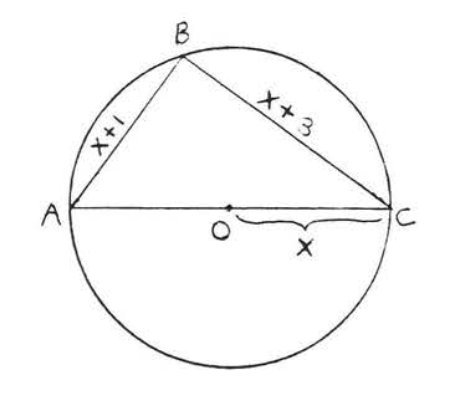
$Screen Shot 2020-12-30 at 12.24.25 PM.png$

Solution

According to Theorem $\PageIndex{2}$ $\angle B = 90^{\circ}$. Therefore $\triangle ABC$ is a right triangle and we can apply the Pythagorean theorem:

\[\begin{array} {rcl} {\text{AB}^2 + \text{BC}^2} & = & {\text{AC}^2} \\ {(x + 1)^2 + (x + 3)^2} & = & {(2x)^2} \\ {x^2 + 2x + 1 + x^2 + 6x + 9} & = & {4x^2} \\ {2x^2 + 8x + 10} & = & {4x^2} \\ {0} & = & {2x^2 - 8x - 10} \\ {0} & = & {x^2 - 4x - 5} \\ {0} & = & {(x - 5)(x + 1)} \end{array}\]

$\begin{array} {rcl} {0} & = & {x - 5} \\ {x} & = & {5} \end{array}$ $\begin{array} {rcl} {0} & = & {x + 1} \\ {x} & = & {-1} \end{array}$

We reject the answer $x = -1$ since $OC = x$ must have positive length.

Check, $x = 5$:

$\text{AB}^2 + \text{BC}^2 = \text{AC}^2$

\[\begin{array} {r|l} {(x + 1)^2 + (x + 3)^2} & {(2x)^2} \\ {(5 + 1)^2 + (5 + 3)^2} & {(2(5))^2} \\ {6^2 + 8^2} & {10^2} \\ {36 + 64} & {100} \\ {100} & {} \end{array}\]

Answer: $x = 5$.

The next four theorems are all consequences of Theorem $\PageIndex{1}$:

Theorem $\PageIndex{3}$

Parallel lines intercept arcs equal in degrees.

In Figure $\PageIndex{9}$ if $AB$ || $CD$ then $\widehat{AC} \stackrel{\circ}{=} \widehat{BD}$.

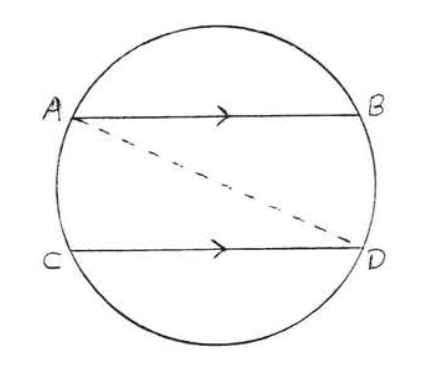$Screen Shot 2020-12-30 at 12.44.27 PM.png$ Figure $\PageIndex{9}$. If $AB$ || $CD$ then $\widehat{AC}$ \stackrel{\circ}{=} $\widehat{BD}$.

Proof: Draw $AD$. Then $\angle ADC \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC}$ and $\angle BAD \stackrel{\circ}{=} \dfrac{1}{2} \widehat{BD}$. Also $\angle ADC = \angle BAD$ because they are alternate interior angles of parallel lines $AB$ and $CD$.Therefore $\dfrac{1}{2} \widehat{AC} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{BD}$ and $\widehat{AC} \stackrel{\circ}{=} \widehat{BD}$.

Example $\PageIndex{8}$

Find $x, y$ and $z$:

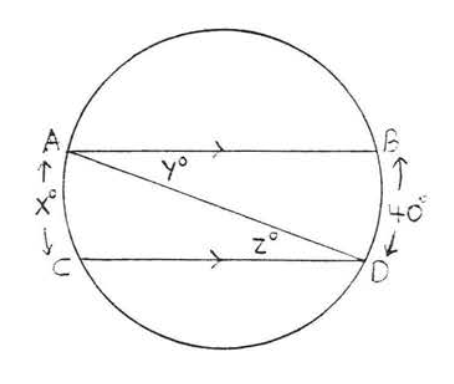
$Screen Shot 2020-12-30 at 12.49.11 PM.png$

Solution

By Theorem $\PageIndex{3}$ $x^{\circ} = 40^{\circ}$. $y^{\circ} = z^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AC} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{BD} \stackrel{\circ}{=} \dfrac{1}{2} (40^{\circ}) = 20^{\circ}$.

Answer: $x = 40, y = z = 20$.

Theorem $\PageIndex{4}$

An angle formed by a tangent and a chord is $\stackrel{\circ}{=} \dfrac{1}{2}$ of its intercepted arc.

In Figure $\PageIndex{10}$ $\angle APC \stackrel{\circ}{=} \dfrac{1}{2} \widehat{PDC}$.

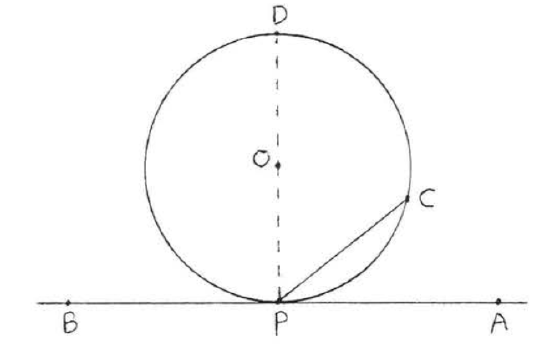$Screen Shot 2020-12-30 at 12.54.05 PM.png$ Figure $\PageIndex{10}$. $\angle APC$ and $\angle BPC$ are formed by tangent $\overleftrightarrow{AB}$ and chord $PC$.

Proof: In Figure $\PageIndex{10}$ draw diameter $PD$. Then by Theorem 7.3.1 of section 7.3 $\angle APD = \angle BPD = 90^{\circ}$. By Theorem $\PageIndex{1}$ of this section $\angle CPD \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CD}$. $\angle APC = 90^{\circ} - \angle CPD \stackrel{\circ}{=} 90^{\circ} - \dfrac{1}{2} \widehat{CD} \stackrel{\circ}{=} 90^{\circ} - \dfrac{1}{2} (180^{\circ} - \widehat{PC}) \stackrel{\circ}{=} 90^{\circ} - 90^{\circ} + \dfrac{1}{2} \widehat{PC} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{PC}$. $\angle BPC = 90^{\circ} + \angle CPD \stackrel{\circ}{=} 90^{\circ} + \dfrac{1}{2} \widehat{CD} \stackrel{\circ}{=} \dfrac{1}{2} (180^{\circ} + \widehat{CD}) \stackrel{\circ}{=} \dfrac{1}{2} \widehat{PDC}$.

Example $\PageIndex{9}$

Find $x, y$ and $\widehat{CD}$:

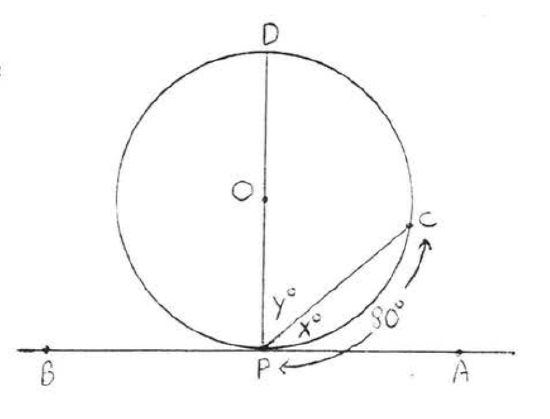
$Screen Shot 2020-12-30 at 1.00.56 PM.png$

Solution

By Theorem $\PageIndex{4}$ $x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{PC} \stackrel{\circ}{=} \dfrac{1}{2} (80^{\circ}) = 40^{\circ}$. $y^{\circ} = 90^{\circ} - x^{\circ} = 90^{\circ} - 40^{\circ} = 50^{\circ}$. $\widehat{CD} \stackrel{\circ}{=} 180^{\circ} - \widehat{CP} \stackrel{\circ}{=} 180^{\circ} - 80^{\circ} = 100^{\circ}$.

Answer: $x = 40$, $y = 50$, $\widehat{CD} \stackrel{\circ}{=} 100^{\circ}$.

Theorem $\PageIndex{5}$

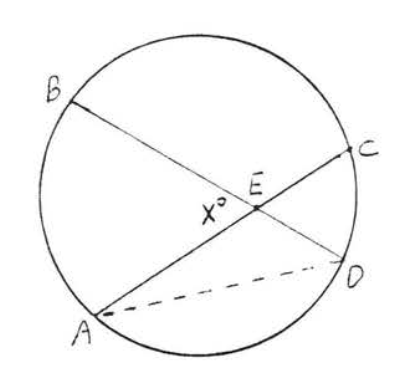
An angle formed by two intersecting chords is $\stackrel{\circ}{=}$ to $\dfrac{1}{2}$ the sum of the intercepted arcs.

In Figure $\PageIndex{11}$ $x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{AB} + \widehat{CD})$.

Screen Shot 2020-12-30 at 1.05.28 PM.png — Figure $\PageIndex{11}$: $x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{AB} + \widehat{CD})$

Proof: $\angle ADB \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB}$ and $\angle CAD \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CD}$. By Theorem 1.5.2, section 1.5, an exterior angle of a triangle is equal to the sum of the two remote interior angles. Therefore $x^{\circ} = \angle ADB + \angle CAD \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB} + \dfrac{1}{2} \widehat{CD} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{AB} + \widehat{CD})$.

Example $\PageIndex{10}$

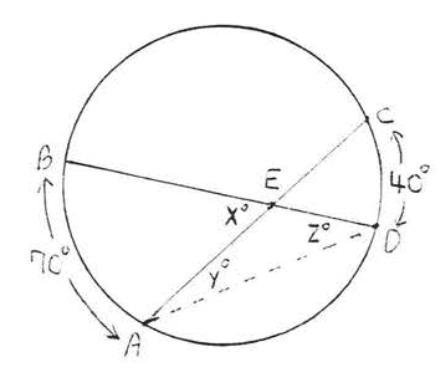
Find $x, y$ and $z$:

$Screen Shot 2020-12-30 at 1.10.51 PM.png$

Solution

By Theorem $\PageIndex{5}$, $x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{AB} + \widehat{CD}) \stackrel{\circ}{=} \dfrac{1}{2} (70^{\circ} + 40^{\circ}) = \dfrac{1}{2}(110^{\circ}) = 55^{\circ}$. $y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CD} = \dfrac{1}{2} (40^{\circ}) = 20^{\circ}$, $z^{\circ} = \dfrac{1}{2} \widehat{AB} = \dfrac{1}{2}(70^{\circ}) = 35^{\circ}$.

Answer: $x = 55, y = 20, z = 35$.

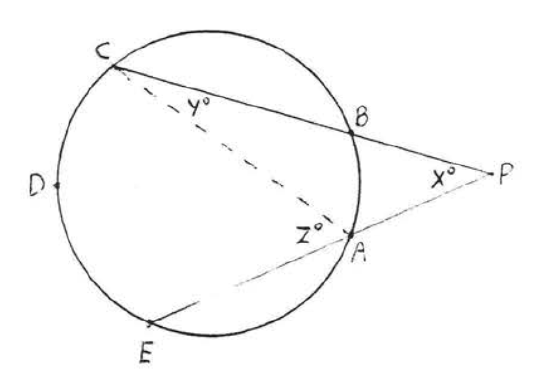
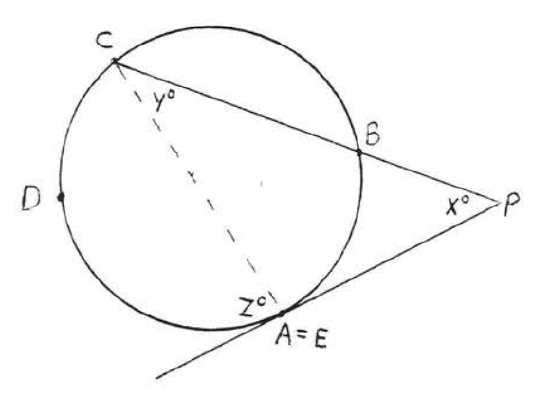
A line which intersects a circle in two points is called a secant. In Figure $\PageIndex{12}$, $PC$ is a secant.

Theorem $\PageIndex{6}$

An angle formed outside a circle by two secants, a tangent and a secant, or two tangents is $\stackrel{\circ}{=} \dfrac{1}{2}$ the difference of the intercepted arcs.

In each of Figures $\PageIndex{12}$, $\PageIndex{13}$ and $\PageIndex{14}$, $\angle P \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{CDE} - \widehat{AB})$.

Screen Shot 2020-12-30 at 1.17.25 PM.png — Figure $\PageIndex{12}$: $\angle P$ formed by two secants.

Screen Shot 2020-12-30 at 1.18.08 PM.png — Figure $\PageIndex{13}$: $\angle P$ formed by a tangent and a secant.

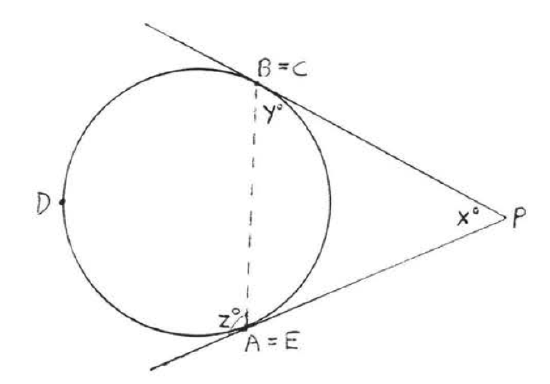
Screen Shot 2020-12-30 at 1.18.54 PM.png — Figure $\PageIndex{14}$: $\angle P$ formed by two tangents.

Proof: In each case $x^{\circ} + y^{\circ} = z^{\circ}$ (because an exterior angle of a triangle is the sum of the two remote interior angles). Therefore $x^{\circ} = z^{\circ} - y^{\circ}$. Using Theorem $\PageIndex{1}$ and $\PageIndex{4}$ we have $\angle P = x^{\circ} = z^{\circ} - y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CDE} - \dfrac{1}{2} \widehat{AB} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{CDE} - \widehat{AB})$.

Example $\PageIndex{11}$

Find $x, y$ and $z$:

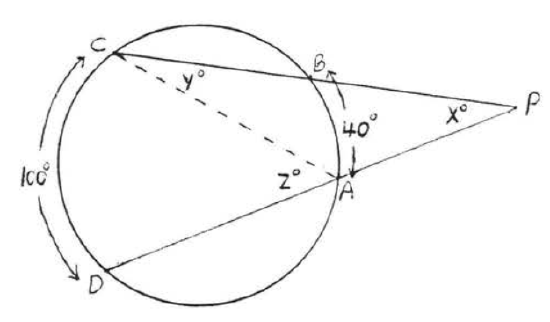
$Screen Shot 2020-12-30 at 1.22.31 PM.png$

Solution

By Theorem $\PageIndex{6}$, $x^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} (\widehat{CD} - \widehat{AB}) \stackrel{\circ}{=} \dfrac{1}{2} (100^{\circ} - 40^{\circ}) = \dfrac{1}{2} (60^{\circ}) = 30^{\circ}$. By Theorem $\PageIndex{1}$, $y^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB} \stackrel{\circ}{=} \dfrac{1}{2} (40^{\circ}) = 20^{\circ}$ and $z^{\circ} \stackrel{\circ}{=} \dfrac{1}{2} \widehat{CD} \stackrel{\circ}{=} \dfrac{1}{2} (100^{\circ}) = 50^{\circ}$.

Answer: $x = 30, y = 20, z = 50$.

Historical Note

The practice of dividing the circle into 360 degrees goes back to the Greeks of the second century B.C., who in turn may have taken it over from the Babylonians. The reason for using the number 360 is not clear. It could stem from an early astronomical assumption that a year consisted of 360 days. Another explanation relies on the fact that the Babylonians used a sexagesimal or base 60 number system instead of the decimal or base 10 system that we use today. It is assumed that the Babylonians may have also used 60 as a convenient value for the radius of a circle. Since the circumference of a circle is about 6 times the radius (see next section), such a circle would consist of 360 units.

Problems

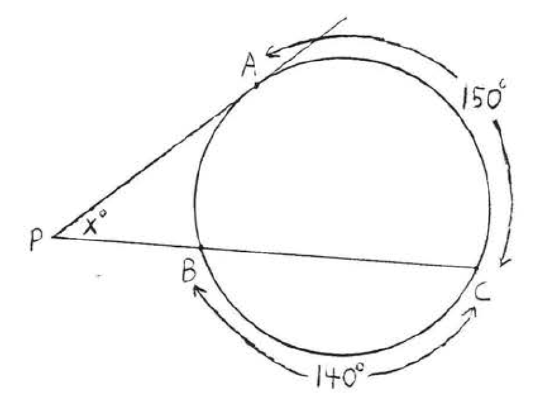
1 - 4. Find the number of degrees in arcs $\widehat{AB}$ and $\widehat{ACB}$:

$Screen Shot 2020-12-30 at 1.33.19 PM.png$

$Screen Shot 2020-12-30 at 1.34.57 PM.png$

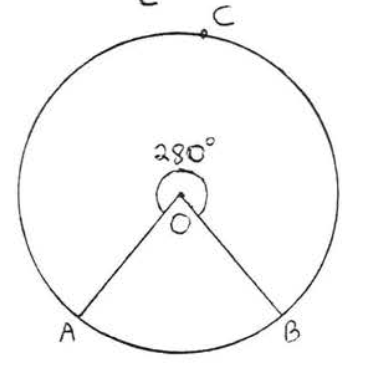
$Screen Shot 2020-12-30 at 1.36.02 PM.png$

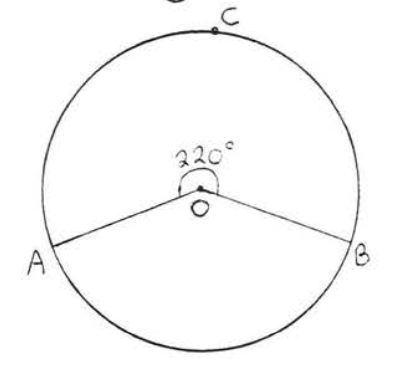
$Screen Shot 2020-12-30 at 1.36.26 PM.png$

5 - 10. Find $x, y$ and $z$:

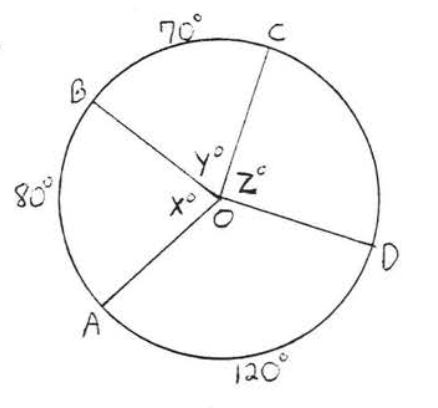
$Screen Shot 2020-12-30 at 1.36.49 PM.png$

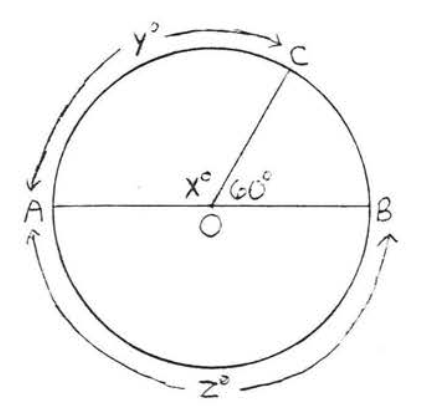
$Screen Shot 2020-12-30 at 1.37.21 PM.png$

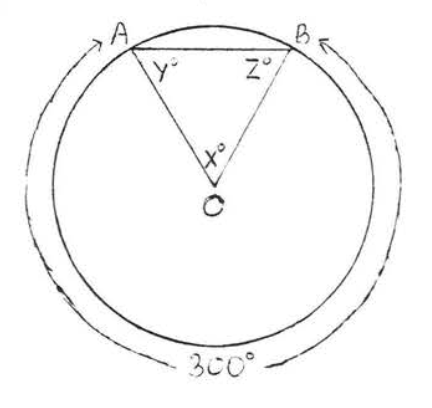
$Screen Shot 2020-12-30 at 1.38.57 PM.png$

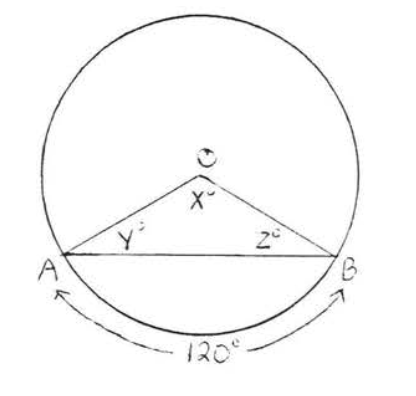
$Screen Shot 2020-12-30 at 1.38.29 PM.png$

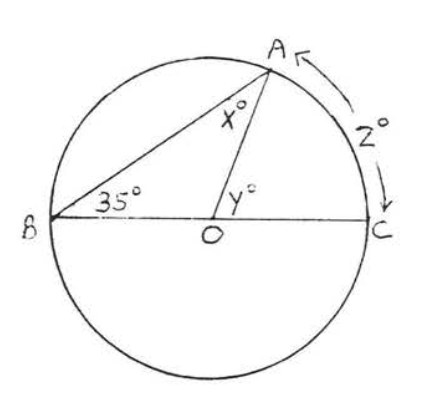
$Screen Shot 2020-12-30 at 1.39.33 PM.png$

10.

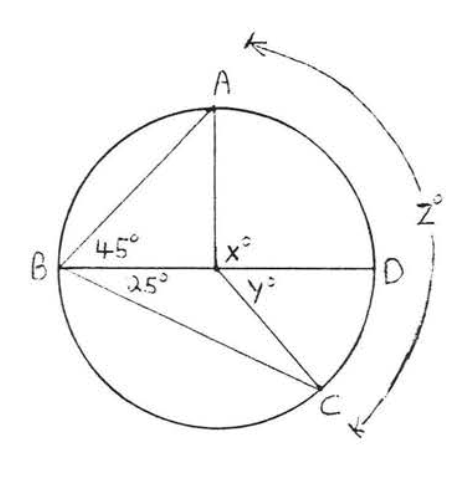
$Screen Shot 2020-12-30 at 1.40.07 PM.png$

11 - 26. Find $x$:

11.

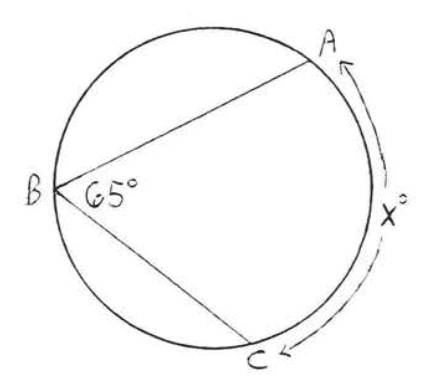
$Screen Shot 2020-12-30 at 1.41.03 PM.png$

12.

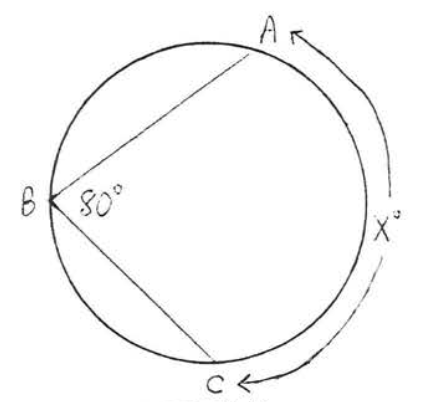
$Screen Shot 2020-12-30 at 1.41.42 PM.png$

13.

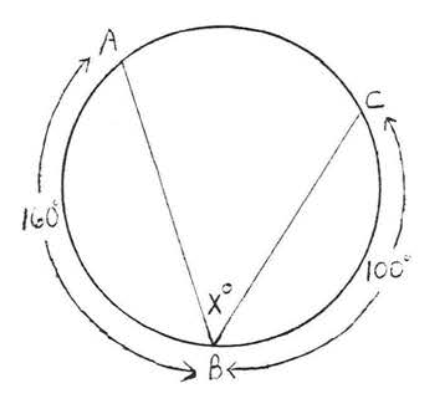
$Screen Shot 2020-12-30 at 1.42.16 PM.png$

14.

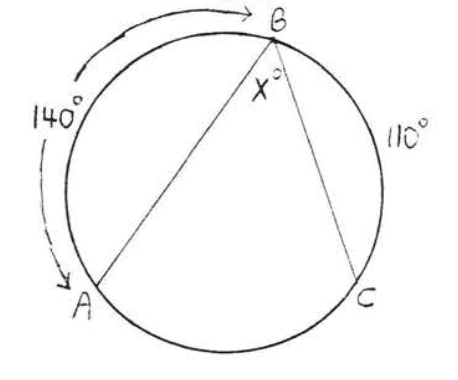
$Screen Shot 2020-12-30 at 1.44.04 PM.png$

15.

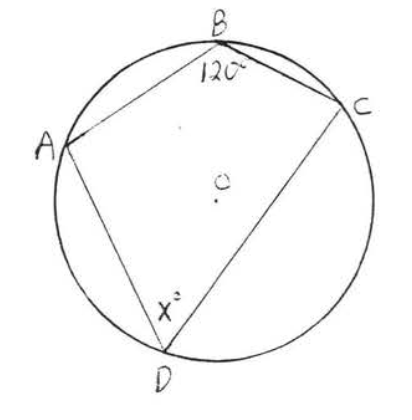
$Screen Shot 2020-12-30 at 1.43.37 PM.png$

16.

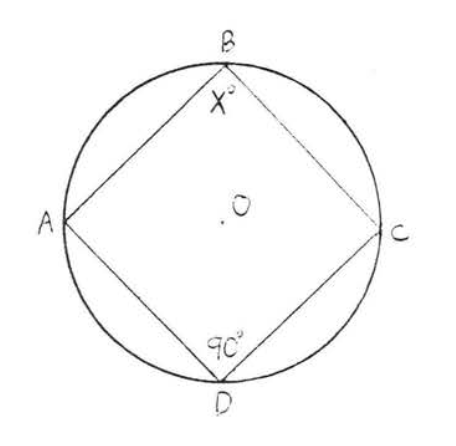
$Screen Shot 2020-12-30 at 1.44.46 PM.png$

17.

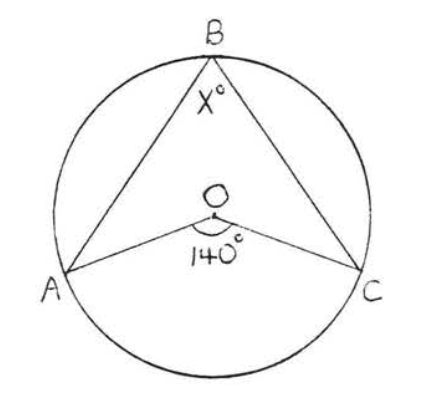
$Screen Shot 2020-12-30 at 1.45.13 PM.png$

18.

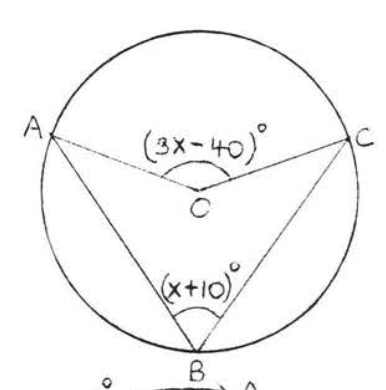
$Screen Shot 2020-12-30 at 1.45.59 PM.png$

19.

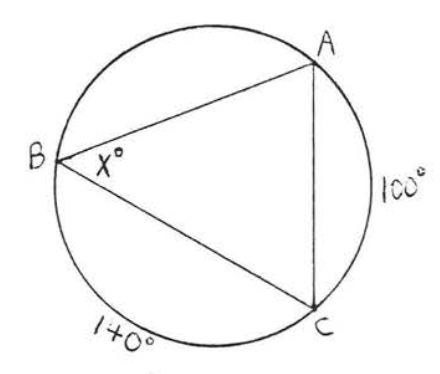
$Screen Shot 2020-12-30 at 1.46.31 PM.png$

20.

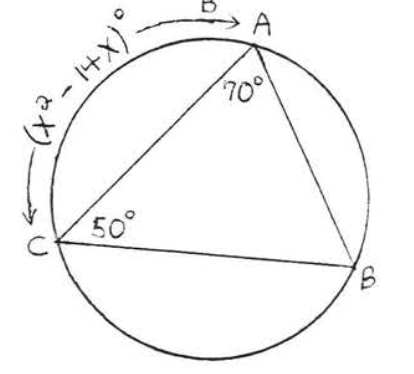
$Screen Shot 2020-12-30 at 1.46.50 PM.png$

21.

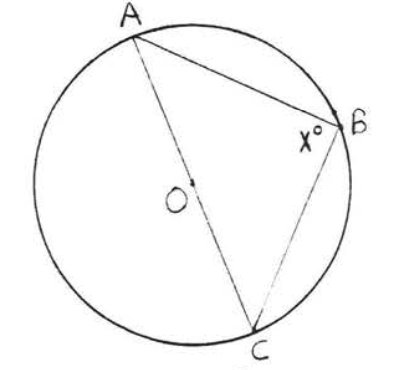
$Screen Shot 2020-12-30 at 1.47.39 PM.png$

22.

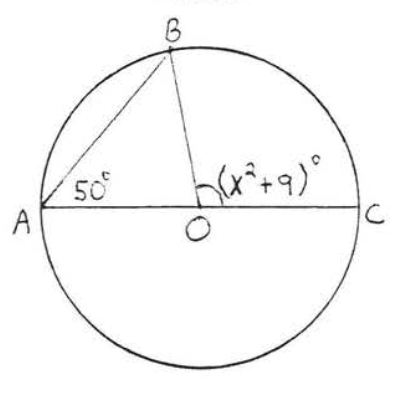
$Screen Shot 2020-12-30 at 1.47.51 PM.png$

23.

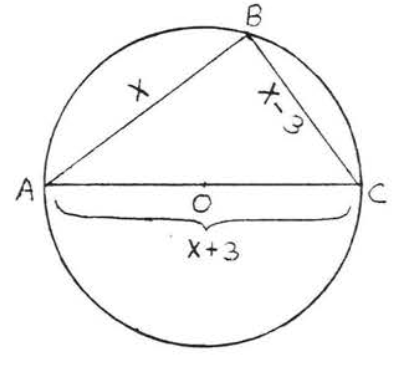
$Screen Shot 2020-12-30 at 1.48.42 PM.png$

24.

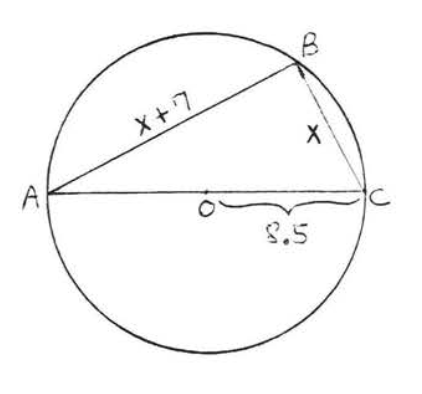
$Screen Shot 2020-12-30 at 1.48.50 PM.png$

25.

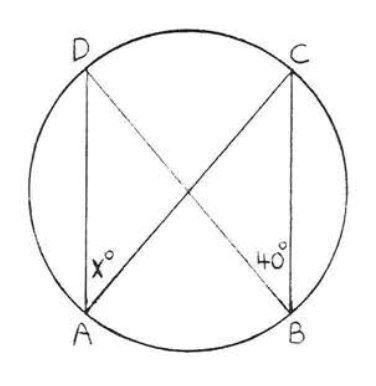
$Screen Shot 2020-12-30 at 1.49.33 PM.png$

26.

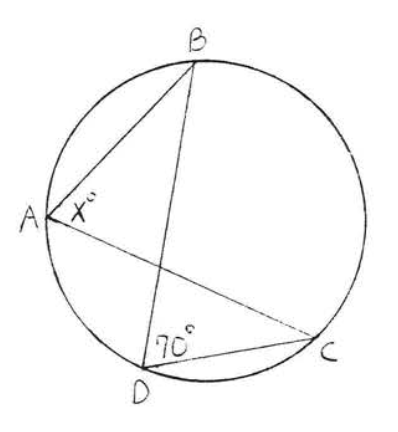
$Screen Shot 2020-12-30 at 1.50.32 PM.png$

27 - 28. Find $x, y$ and $z$:

27.

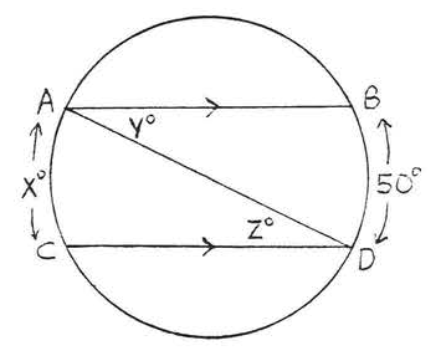
$Screen Shot 2020-12-30 at 1.51.18 PM.png$

28.

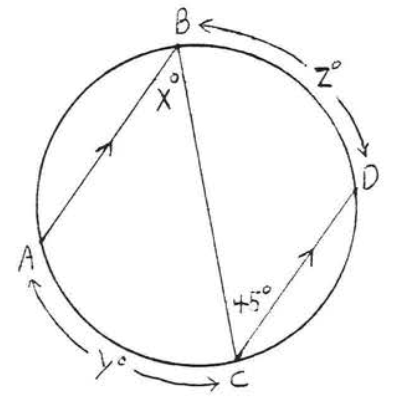
$Screen Shot 2020-12-30 at 1.52.28 PM.png$

29 - 30. Find $x$:

29.

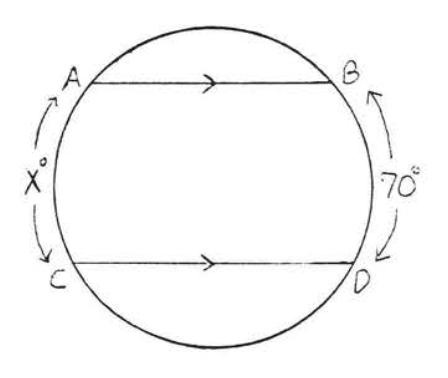
$Screen Shot 2020-12-30 at 1.52.59 PM.png$

30.

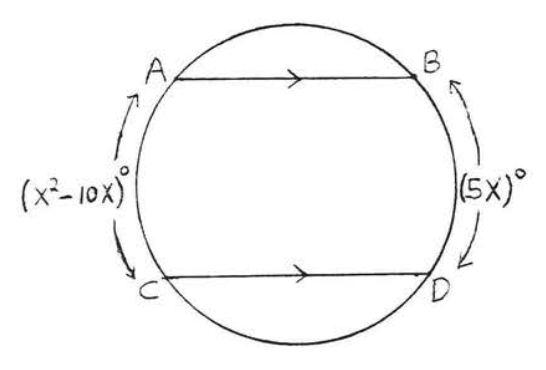
$Screen Shot 2020-12-30 at 1.54.13 PM.png$

31 - 32. Find $x, y$ and $z$:

31.

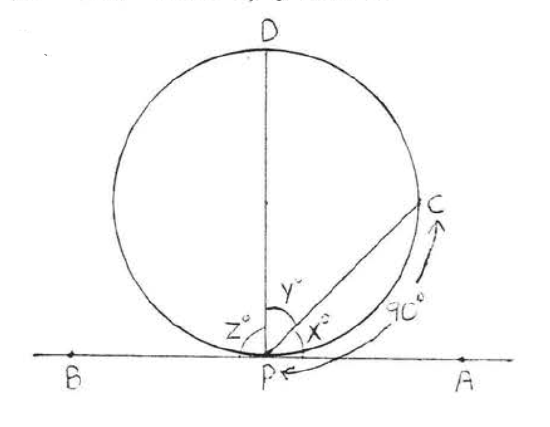
$Screen Shot 2020-12-30 at 1.53.42 PM.png$

32.

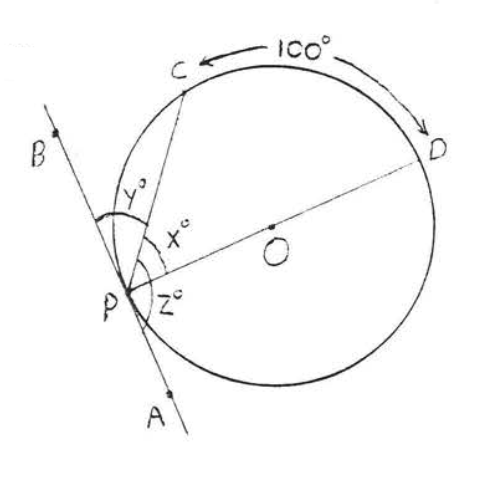
$Screen Shot 2020-12-30 at 1.54.50 PM.png$

33 - 34. Find $x$:

33.

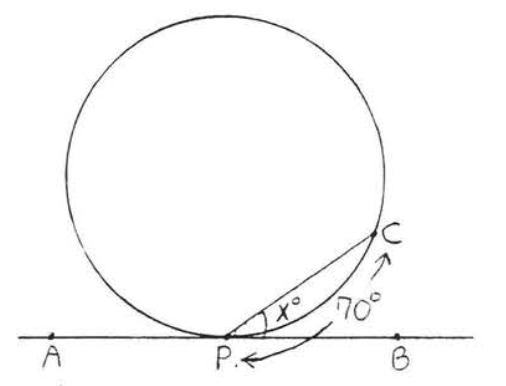
$Screen Shot 2020-12-30 at 1.55.35 PM.png$

34.

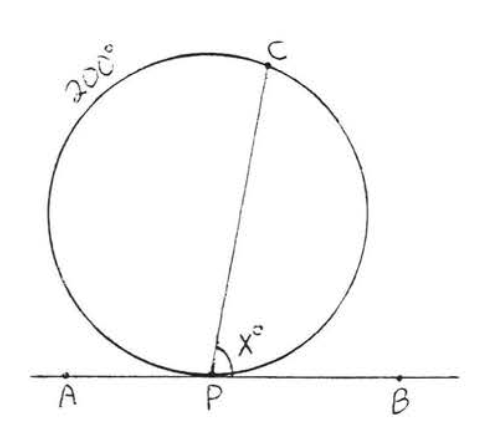
$Screen Shot 2020-12-30 at 1.55.57 PM.png$

35 - 36. Find $x$, $y$ and $z$:

35.

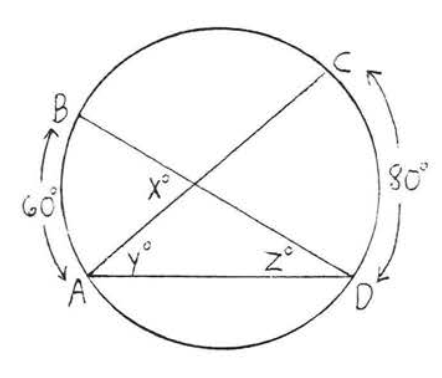
$Screen Shot 2020-12-30 at 1.56.25 PM.png$

36.

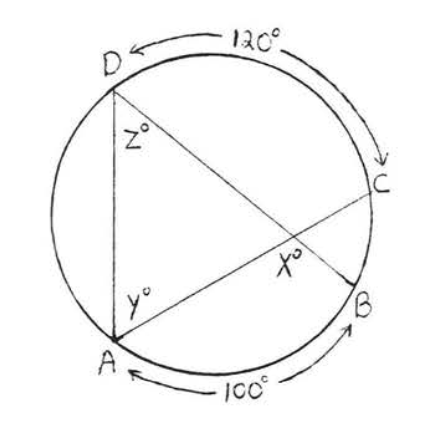
$Screen Shot 2020-12-30 at 1.56.35 PM.png$

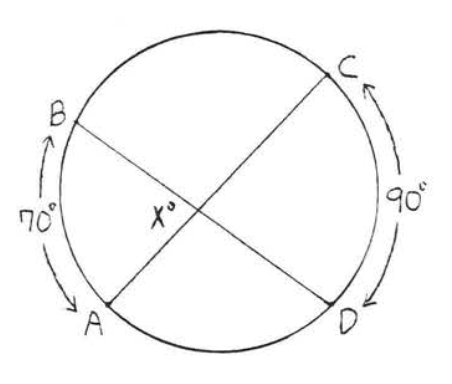
37 - 38. Find $x$:

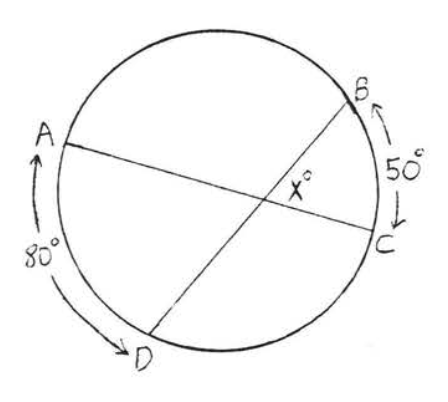
37.

$Screen Shot 2020-12-30 at 1.57.18 PM.png$

38.

$Screen Shot 2020-12-30 at 1.57.51 PM.png$

39 - 42. Find $x, y$ and $z$:

39.

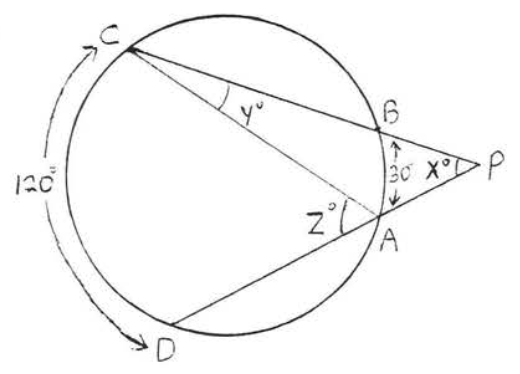
$Screen Shot 2020-12-30 at 1.58.19 PM.png$

40.

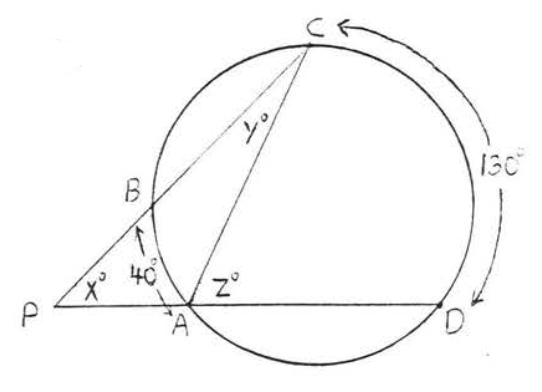
$Screen Shot 2020-12-30 at 1.59.22 PM.png$

41.

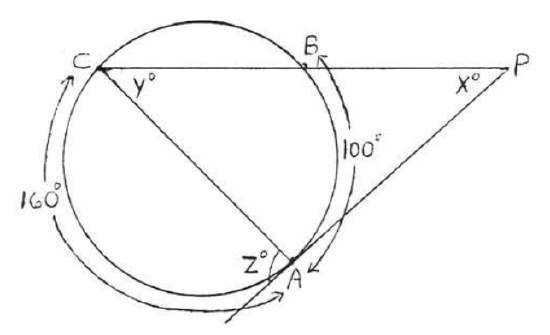
$Screen Shot 2020-12-30 at 2.00.01 PM.png$

42.

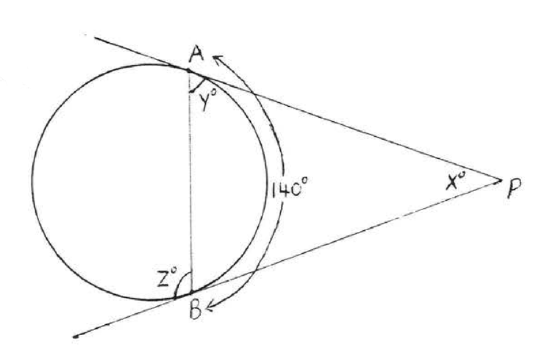
$Screen Shot 2020-12-30 at 2.00.30 PM.png$

43 - 46. Find $x$:

43.

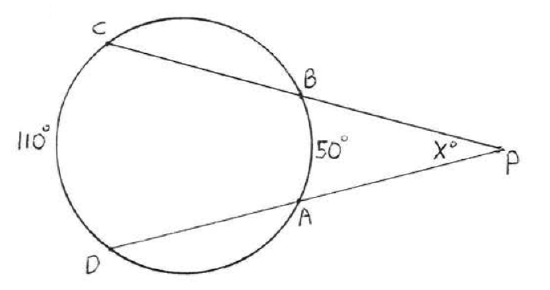
$Screen Shot 2020-12-30 at 2.01.14 PM.png$

44.

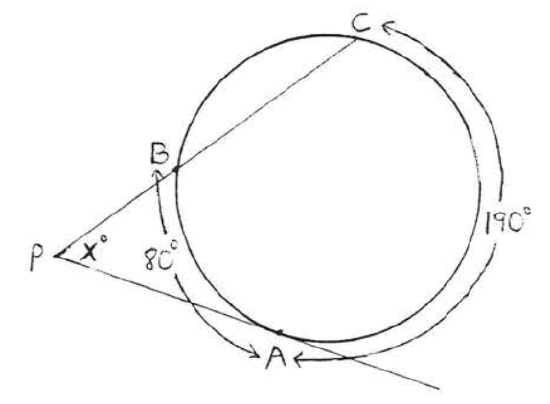
$Screen Shot 2020-12-30 at 2.01.24 PM.png$

45.

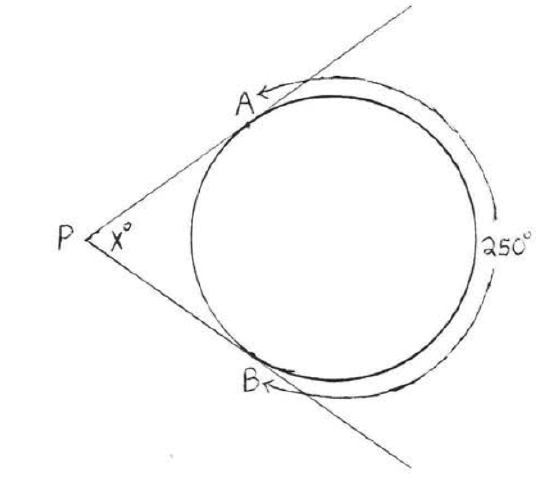
$Screen Shot 2020-12-30 at 2.01.59 PM.png$

46.

$Screen Shot 2020-12-30 at 2.02.25 PM.png$

Example \(\PageIndex{1}\)

Example \(\PageIndex{1}\)

Theorem \(\PageIndex{1}\)

Example \(\PageIndex{3}\)

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Theorem \(\PageIndex{2}\)

Example \(\PageIndex{7}\)

Theorem \(\PageIndex{3}\)

Example \(\PageIndex{8}\)

Theorem \(\PageIndex{4}\)

Example \(\PageIndex{9}\)

Theorem \(\PageIndex{5}\)

Example \(\PageIndex{10}\)

Theorem \(\PageIndex{6}\)

Example \(\PageIndex{11}\)

Historical Note

Problems