7.5: Circumference of a Circle
- Page ID
- 34156
The circumference of a circle is the perimeter of the circle, the length of the line obtained by cutting the circle and "straightening out the curves" (Figure \(\PageIndex{1}\)).
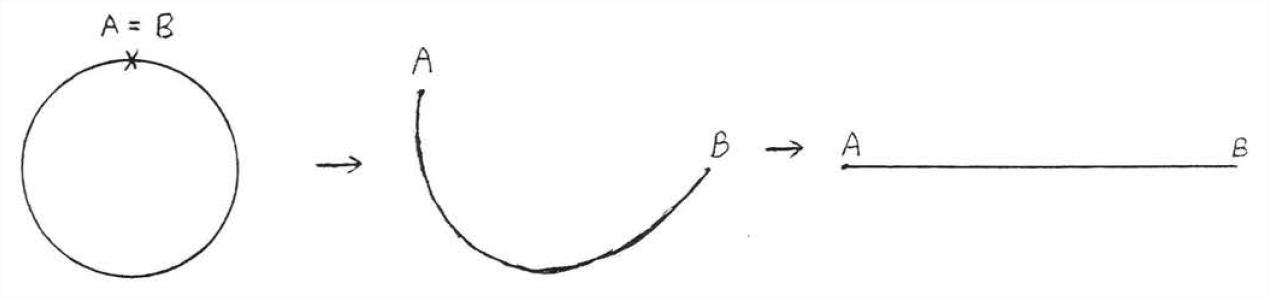
It is impractical to measure the circumference of most circular objects directly. A circular tape measure would be hard to hold in place and would become distorted as it would be bent. The object itself would be destroyed if we tried to cut it and straighten it out for measurement. Fortunately we can calculate the circumference of a circle from its radius or diameter, which are easy to measure.
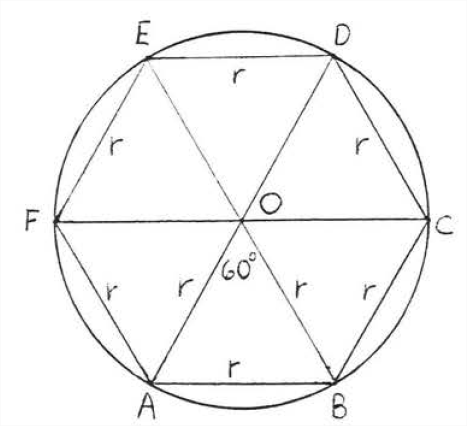
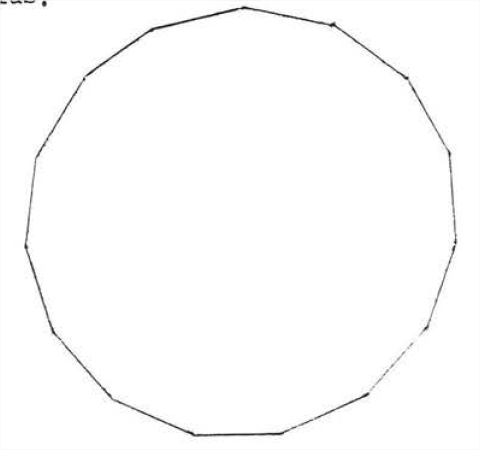
An approximate value for the circumference of a circle of radius \(x\) can be obtained by calculating the perimeter of a regular hexagon of radius \(r\) inscribed in the circle (Figure \(\PageIndex{2}\)). We see that the circumference is a little more than the perimeter of the hexagon, which is 6 times the radius ox 3 times the diameter. To get a better approximation, we increase the number of sides of the inscribed regular polygon. As the number of sides of a regular polygon increases, the polygon looks more and more like a circle (Figure \(\PageIndex{3}\)). In Section 7.1, we calculated the perimeter of a 90-sided regular polygon to be 3.141 times the diameter or 6.282 times the radius. The perimeter of a 1000-sided regular polygon turned out to be only slightly larger, 3.1416 times the diameter or 6.283 times the radius. It therefore seems reasonable to conclude that the circumference of a circle is about 3.14 times its diameter or 6.28 times its radius.
The circumference of a circle is \(\pi\) times its diameter or \(2 \pi\) times its radius, where \(\pi\) is approximately 3.14.
\[C=\pi d\]
or
\[C =2 \pi r\]
The symbol \(\pi\) (Greek letter pi) is standard notation for the number by which the diameter of a circle must be multiplied to get the circumference. Its value is usually taken to be 3.14, though 3.1416 and \(\dfrac{22}{7}\) are other commonly used approximations. These numbers are not exact, for like \(\sqrt{2}\), it can be shown that \(\pi\) is an irrational number (infinite nonrepeating decimal). Its value to 50 decimal places is
3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37511
Find the circumference:
Solution
\(C = \pi d = (3.14)(4) = 12.56\).
Answer: 12.56
We define the length of an arc in the same manner as we defined circumference. We calculate it by multiplying the circumference by the appropriate fraction.
Find the length of arc \(\widehat{AB}\):
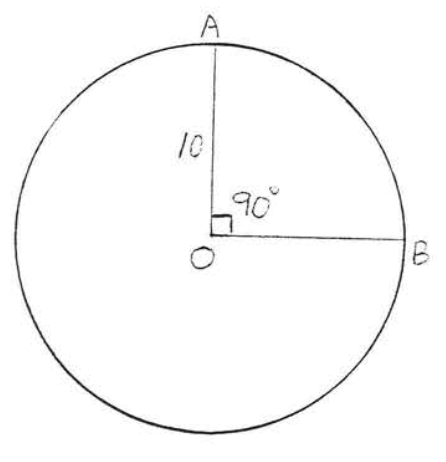
Solution
\(C = 2\pi r = 3(3.14)(10) = 62.8\). Since \(90^{\circ}\) is \(\dfrac{1}{4}\) of \(360^{\circ}\), \(\widehat{AB}\) is \(\dfrac{1}{4}\) of the circumference \(C\). \(\widehat{AB} = \dfrac{1}{4} C = \dfrac{1}{4} (62.8) = 15.7\).
Answer: 15.7.
As we stated in section 7.4, the plain = symbol will be used for arc length and the \(\stackrel{\circ}{=}\) symbol will be used for degrees. Thus in Example \(PageIndex{2}\), \(\widehat{AB} = 15.7\) but \(\widehat{AB} \stackrel{\circ}{=} 90^{\circ}\).
We may also use the following formula to find arc length:
\[\text{Arc Length} = \dfrac{\text{Degrees in Arc}}{360^{\circ}} \cdot \text{Circumference}\]
or simply
\[L = \dfrac{D}{360} \cdot C\]
Thus in Example \(\PageIndex{2}\),
\(L = \dfrac{D}{360} \cdot C = \dfrac{90}{360} (62.8) = \dfrac{1}{4} (62.8) = 15.7\)
Find the length of arc \(\widehat{AB}\):
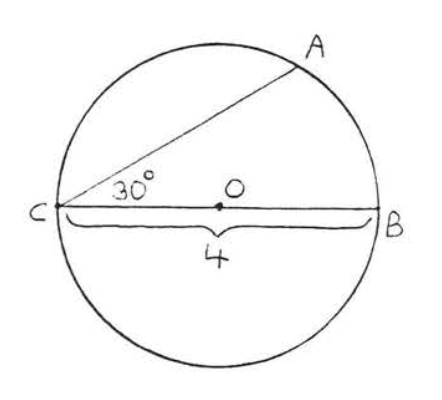
Solution
\(C = \pi d =(3.14)(4) = 12.56\). \(\angle ACB \stackrel{\circ}{=} \dfrac{1}{2} \widehat{AB} \stackrel{\circ}{=} 30^{\circ}\). Therefore \(\widehat{AB} \stackrel{\circ}{=} 60^{\circ}\). Using the formula for arc length,
\(L = \dfrac{D}{360} C = \dfrac{60}{360} (12.56) = \dfrac{1}{6} (12.56) = 2.09\).
Answer: 2.09.
Find the diameter of a circle whose circumference is 628.
Solution
Letting \(C = 628\) and \(\pi = 3.14\) in the formula for circumference, we have
\[\begin{array} {rcl} {c} & = & {\pi d} \\ {628} & = & {(3.14) d} \\ {\dfrac{628}{3.14}} & = & {\dfrac{3.14d}{3.14}} \\ {200} & = & {d} \end{array}\]
Answer: diameter = 200.
The odometer and speedometer of an automobile are calibrated in accordance with the number of rotations of one of the wheels. Suppose the diameter of a tire mounted on the wheel is 2 feet. Then its circumference is \(C = \pi d = (3.14)(2) = 6.28\) feet. Since 1 mile = 5280 feet, the wheel will rotate \(5280 \div 6.28 = 841\) times every mile. If the size of the tires is changed for any reason the odometer and speedometer must be recalibrated.
The circumference of the earth was first accurately calculated by the Greek geographer Eratosthenes (c. 284 - 192 B.C.), who lived in Alexandria, Egypt. It was known that at noon on the day of the summer solstice the sun's rays completely lit up the wells of Syene (now called Aswan), Egypt. This indicated that the rays of the sun were perpendicular to the Earth's surface at Syene, and so, in Figure \(\PageIndex{4}\), \(\overleftrightarrow{DS}\) passes through the earth's center \(O\). At the same time, in Alexandria, Eratosthenes observed that the sun's rays were making an angle of \(\dfrac{1}{50}\) of \(360^{\circ}\) (that is, \(7.2^{\circ}\)) with the perpendicular (\(\angle BAC = 7.2^{\circ}\) in Figure \(\PageIndex{4}\)). The rays of the sun are assumed to be parallel hence \(\angle AOS = \angle BAC = 7.2^{\circ}\) and \(\widehat{AS} \stackrel{\circ}{=} 7.2^{\circ}\). Since the distance between Alexandria and Syene is about 500 miles (the length of \(\widehat{AS}\)). Eratosthenes was able to come up with a remarkably accurate figure of about (50)(500) = 25,000 miles for the circumference of the earth.
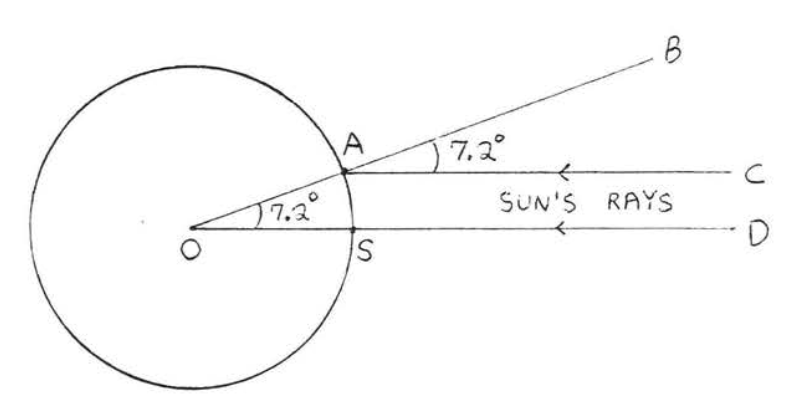
Figure \(\PageIndex{4}\). The sun's rays were perpendicular to the Earth's surface at \(S\) at the same time they were making an angle of \(7.2^{\circ}\) with the perpendicular at \(A\).
Early crude estimates of the value of \(\pi\) were made by the Chinese (\(\pi = 3\)), Babylonians (\(\pi = 3\) or \(3\dfrac{1}{8}\)), and Egyptians (\(\pi = 3.16\)). The value \(\pi = 3\) is also the one assumed in the Bible (I Kings 7:23). The first accurate calculation was carried out by Archimedes (287 - 212 B.C.), the greatest mathematician of antiquity, (Archimedes was also a famous physicist and inventor. For example, he discovered the principle that a solid immersed in a liquid is buoyed up by a force equal to the weight of the fluid displaced.) In his treatise On the Measurement of the Circle he approximates the circumference by calculating the perimeters of inscribed and circumscribed regular polygons (Figure \(\PageIndex{5}\)). This is similar to the method we described in the text except that Archimedes did not have accurate trigonometric tables and had to derive his own formulas, By carrying the process as far as the case of the polygon of 96 sides he found the value of to be between \(3\dfrac{10}{71}\) and \(3 \dfrac{1}{7}\). (Incidentally Archimedes did not actually use the symbol \(\pi\). The symbol \(\pi\) was not used for the ratio of the circumference to the diameter of a circle until the 18th century.)
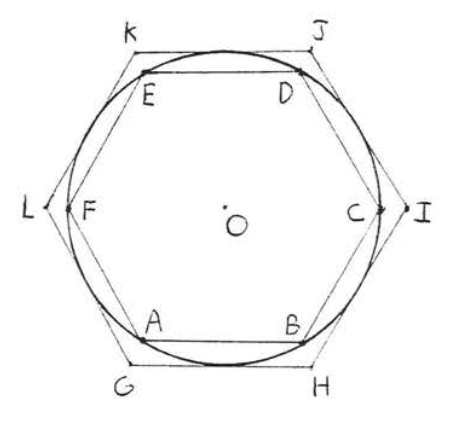
The procedure of Archimedes was the beginning of a long histors; of increasingly accurate calculations of the value of \(\pi\). Since the 17th century these calculations have involved the use of infinite series, such as
\[\dfrac{1}{4}\pi = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \dfrac{1}{7} + \dfrac{1}{9} - ...\]
the derivation of which ca.Tl be found in many calculus textbooks. Most recently, with the help of a computer, the value of \(\pi\) has been determined to a million decimal places.
PROBLEMS
For each of the following use \(\pi = 3.14\).
1 - 8. Find the circumference of each circle:
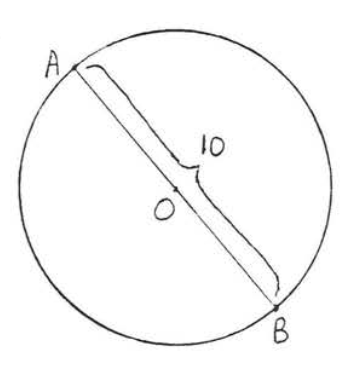
1.
2.
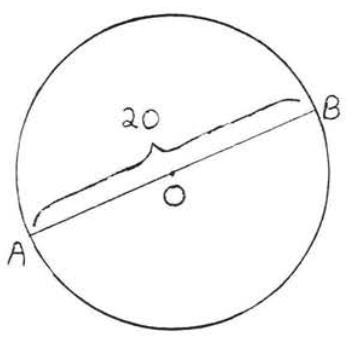
3.
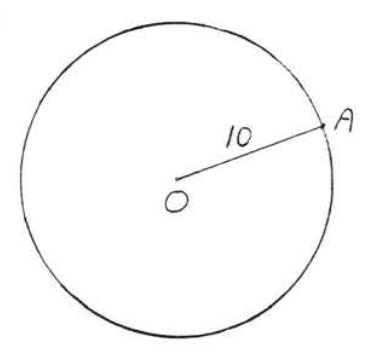
4.
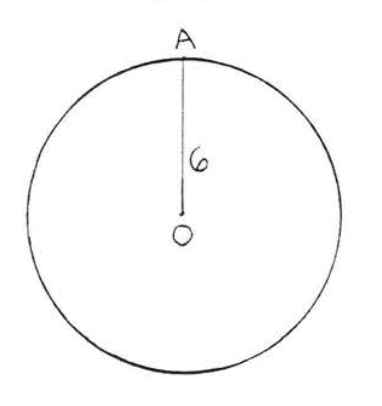
5.
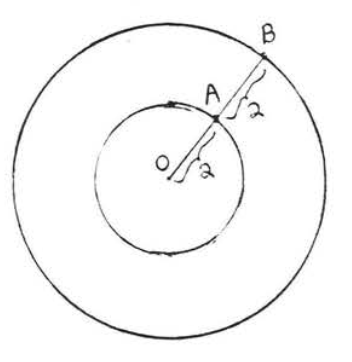
6.
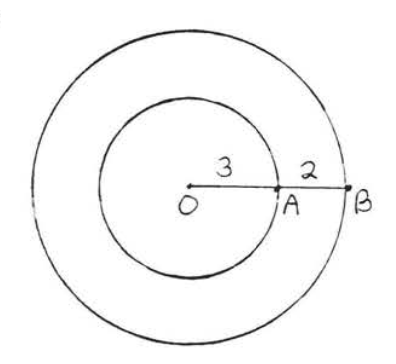
7.
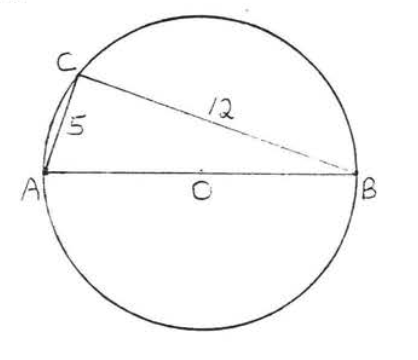
8.
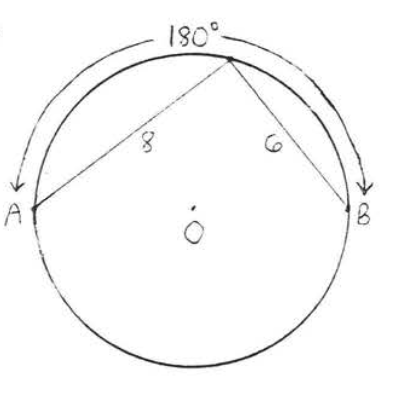
9 - 14. Find the length of arc \(\widehat{AB}\):
9.
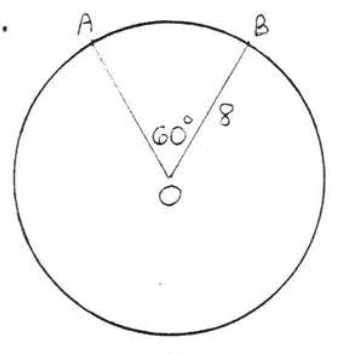
10.
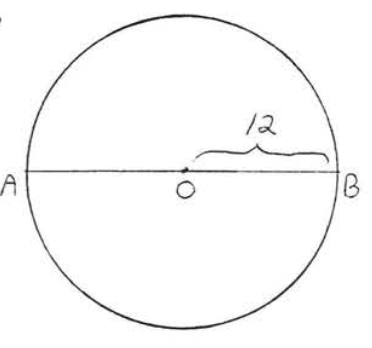
11.
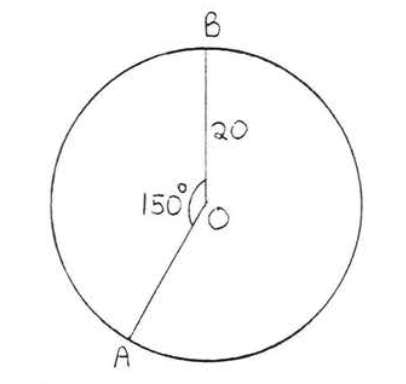
12.
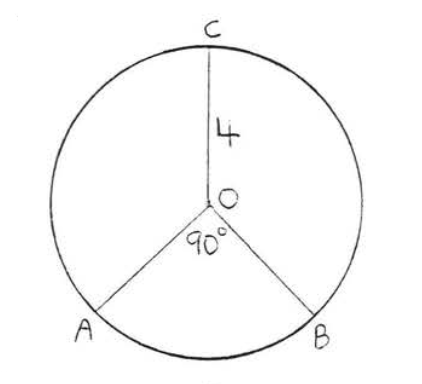
13.
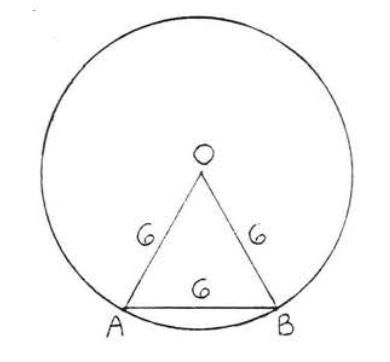
14.
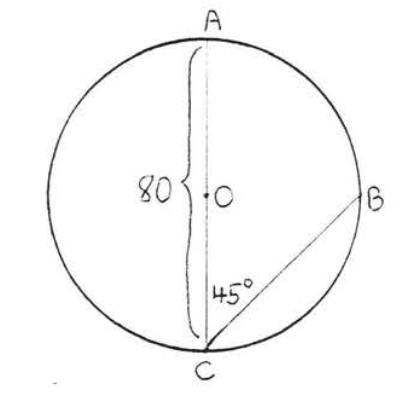
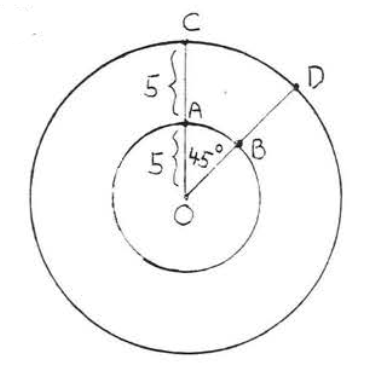
15 - 16. Find the lengths of arcs \(\widehat{AB}\) and \(\widehat{CD}\):
15.
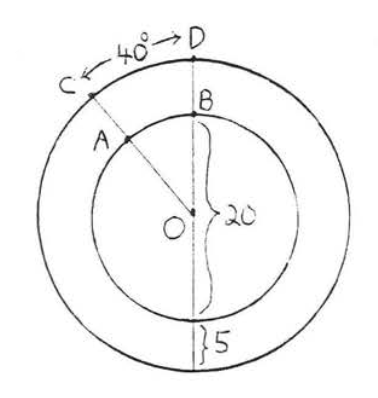
16.
17 - 18. Find the length of major arc \(\widehat{ABC}\):
17.
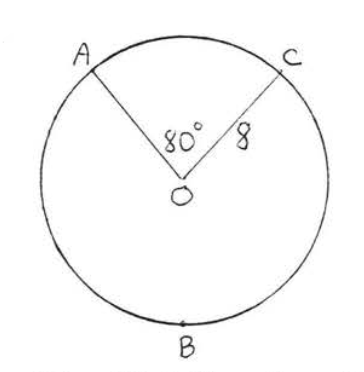
18.
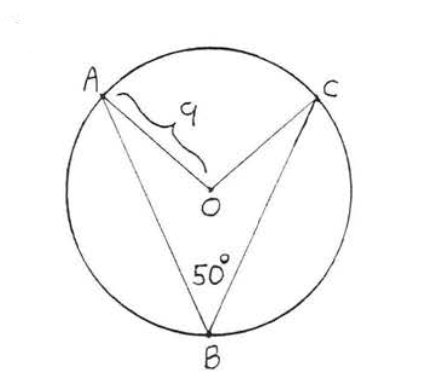
19 - 22. Find the circumference of the circle whose...
19. diameter is 30.
20. diameter is 8.
21. radius is 10.
22. radius is 6.
23. Find the radius and diameter of the circle whose circumference is 314.
24. Find the radius and diameter of the circle whose circumference is 100 (leave answer to the nearest whole number).
25. What is the circumference of an automobile wheel whose diameter is 14 inches?
26. What is the circumference of a 12 inch phonograph record?
27. What is the diameter of the earth if its circumference is 24,830 miles?
28. What is the diameter of a quarter mile circular running track?


