7.6: Area of a Circle
- Page ID
- 34157
In chapter VI we defined the area of a closed figure to be the number of square units contained in the figure. To apply this definition to the circle, we will again assume a circle is a regular polygon with a large number of sides. The following formula is then obtained:
The area of circle is \(\pi\) times the square of its radius.
\[A = \pi r^2\]
- Proof
-
The area of a circle with radius \(r\) is approximately equal to the area of a regular polygon with apothem \(a =r\) circumscribed about the circle (Figure \(\PageIndex{1}\)). The approximation becomes more exact as the number of sides of the polygon becomes larger. At the same time the perimeter of the polygon approximates the circumference of the circle (= \(2\pi r\)).
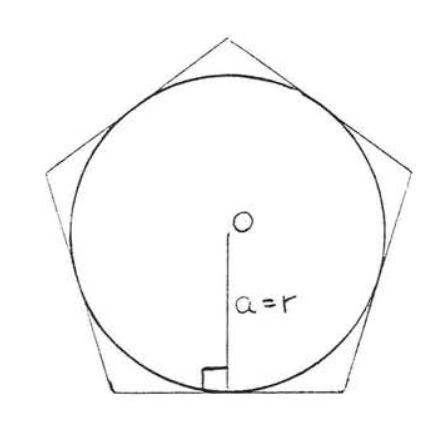
Figure \(\PageIndex{1}\): Regular polygon with apothem \(a = r\) circumscribed about circle with radius \(r\).
Find the area of the circle:
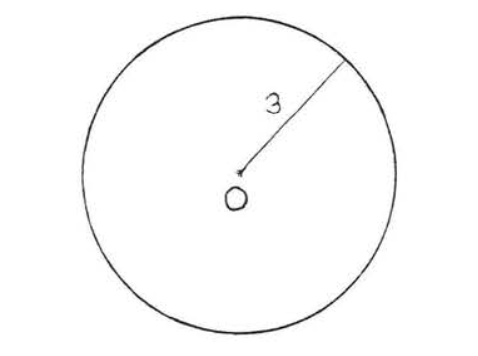
Solution
\(A = \pi r^2 = \pi (3)^2 = 9\pi = 9(3.14) = 28.26\)
Answer: 28.26
Using the formula for the area of a regular polygon (Theorem 7.1.4, section 7.1) we have
\[\text{area of circle} = \text{area of polygon} = \dfrac{1}{2}aP = \dfrac{1}{2} r(2\pi r) = \pi r^2.\]
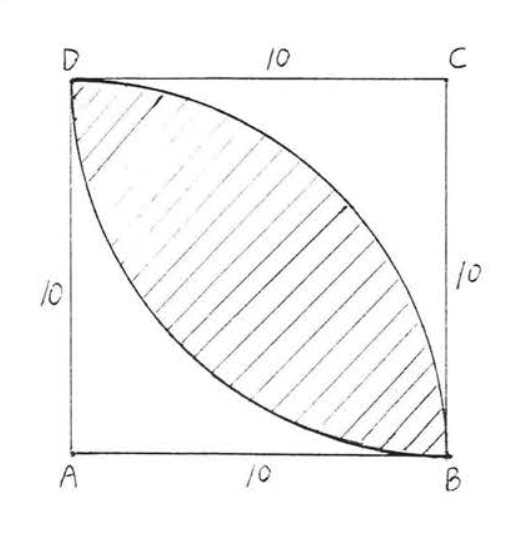
Find the shaded area:
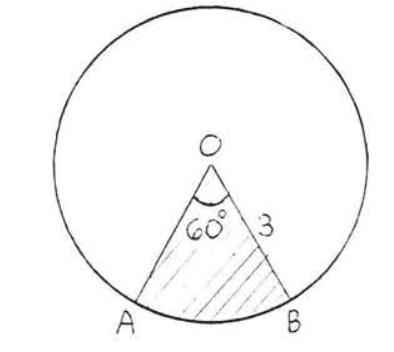
Solution
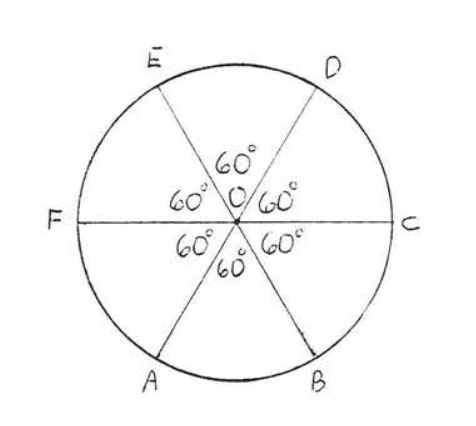
The shaded area \(OAB\) is \(\dfrac{60}{360} = \dfrac{1}{6}\) of the total area (see Figure \(\PageIndex{2}\)). The area of the whole circle = \(\pi r^2 = \pi (3)^2 = 9\pi = 9(3.14) = 28.26\). Therefore the area of \(OAB = \dfrac{1}{6} (28.26) = 4.71\).
Answer: 4.71
The shaded area in Example \(\PageIndex{2}\) is called a sector of the circle. Example \(\PageIndex{2}\) suggests the following formula for the area of a sector:
\[\text{Area of sector} = \dfrac{\text{Degrees in arc of sector}}{360} \cdot \text{Area of circle}\]
or simply
\[A = \dfrac{D}{360} \pi r^2\]
Using this formula, the solution of Example \(\PageIndex{2}\) would be
\[A = \dfrac{D}{360} \pi r^2 = \dfrac{60}{360} (3.14)(3)^2 = \dfrac{1}{6} (3.14)(9) = \dfrac{1}{6} (28.26) = 4.71\]
Find the shaded area:
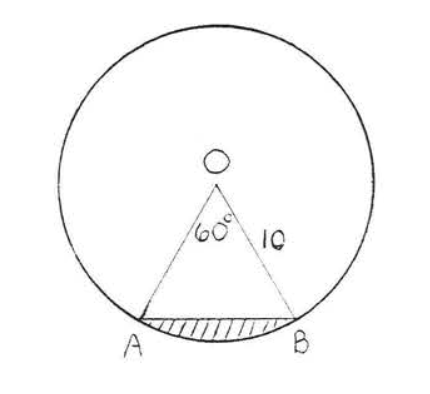
Solution
Let us first find the area of triangle \(OAB\) (Figure \(\PageIndex{3}\)).
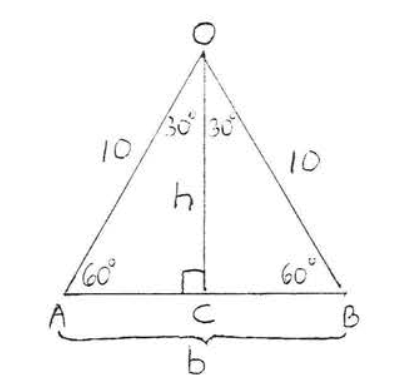
\(\triangle OAB\) is equilateral with base \(b = AB = 10\). Drawing in height \(h = OC\) we have that \(\triangle AOC\) is a \(30^{\circ} - 60^{\circ} -90^{\circ}\) triangle with \(AC = 5\) and \(h = 5\sqrt{3}\). Therefore area of \(\triangle OAB = \dfrac{1}{2} bh = \dfrac{1}{2} (10) (5\sqrt{3}) = 25 \sqrt{3}\). Therefore
\[\begin{array} {rcl} {\text{shaded area}} & = & {\text{area of sector } OAB - \text{area of triangle } OAB} \\ {} & = & {\dfrac{D}{360} \pi r^2 - \dfrac{1}{2} bh} \\ {} & = & {\dfrac{60}{360} \pi (10)^2 - \dfrac{1}{2} (10) (5\sqrt{3})} \\ {} & = & {\dfrac{1}{6} (100\pi) - \dfrac{1}{2} (50\sqrt{3})} \\ {} & = & {\dfrac{50\pi}{3} - 25\sqrt{3}} \\ {} & = & {\dfrac{50(3.14)}{3} - 25(1.732)} \\ {} & = & {52.33 - 43.30 = 9.03} \end{array}\]
Answer: \(\dfrac{50\pi}{3} - 25\sqrt{3}\) or 9.03.
The shaded area in Example \(\PageIndex{3}\) is called a segment of the circle. The area of a segment is obtained by subtracting the area of the triangle from the area of the sector.
Find the shaded area:
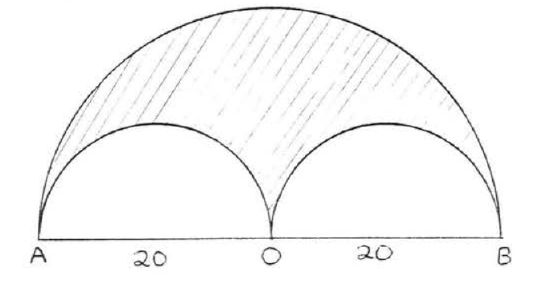
Solution
The area of the large semicircle = \(\dfrac{1}{2} \pi r^2 = \dfrac{1}{2} \pi (20)^2 = \dfrac{1}{2} (400) \pi = 200 \pi\). The area of each of the smaller semicircles = \(\dfrac{1}{2} \pi r^2 = \dfrac{1}{2} \pi (10)^2 = \dfrac{1}{2} (100) \pi = 50\pi\). Therefore
\[\begin{array} {rcl} {\text{shaded area}} & = & {\text{area of large semicircle - (2)(area of small semicircles)}} \\ {} & = & {200 \pi - 2(50\pi)} \\ {} & = & {200\pi - 100\pi} \\ {} & = & {100 \pi = 100 (3.14) = 314} \end{array}\]
Answer: \(100 \pi\) or 314.
Problem 50 of the Rhind Papyrus, a mathematical treatise written by an Egyptian scribe in about 1650 B.C., states that the area of a circular field with a diameter of 9 units is the same as the area of a square with a side of 8 units. This is equivalent to using the formula \(A = (\dfrac{8}{9} d)^2\) to find the area of a circle. If we let \(d = 2r\) this becomes \(A = (\dfrac{8}{9} d)^2 = (\dfrac{8}{9} \cdot 2r)^2 = (\dfrac{16}{9} r)^2 = \dfrac{256}{81} r^2\) or about \(3.16 r^2\). Comparing this with our modern formula \(A = \pi r^2\) we find that the ancient Egyptains had a remarkably good approximation, 3.16, for the value of \(\pi\).
In the same work in which he calculated the value of \(\pi\), Archimedes gives a formula for the area of a circle (see Historical Note, section 7.5). He states that the area of a circle is equal to the area of a right triangle whose base \(b\) is as long as the circumference and whose altitude \(h\) equals the radius. Letting \(b = C\) and \(h = r\) in the formula for the area of a triangle, we obtain \(A = \dfrac{1}{2} bh = \dfrac{1}{2} Cr = \dfrac{1}{2} (2\pi r) = \pi r^2\), the modern formula.
PROBLEMS
1 - 6. Find the area of the circle (use \(\pi = 3.14\)):
1.
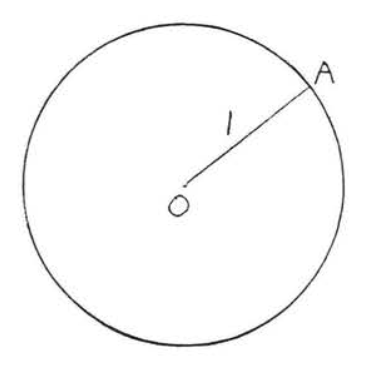
2.
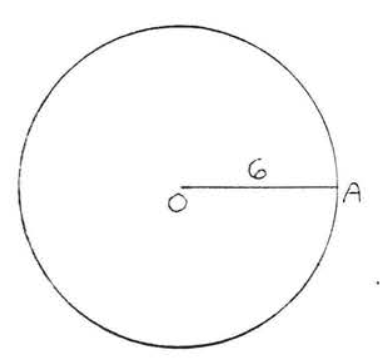
3.
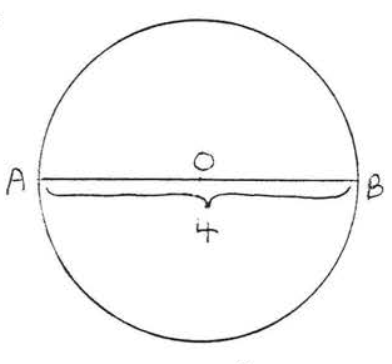
4.
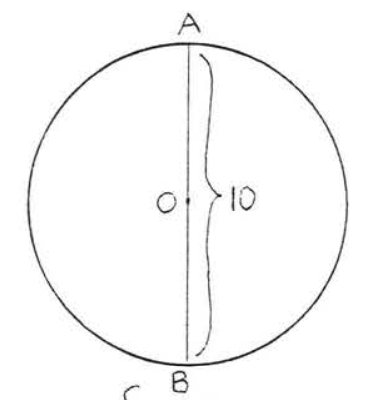
5.
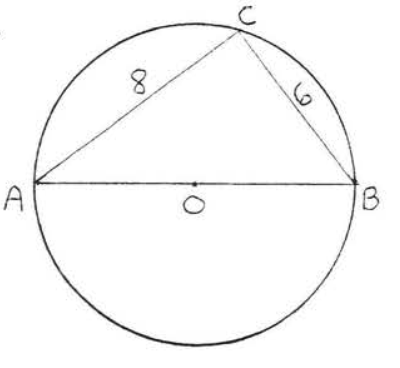
6.
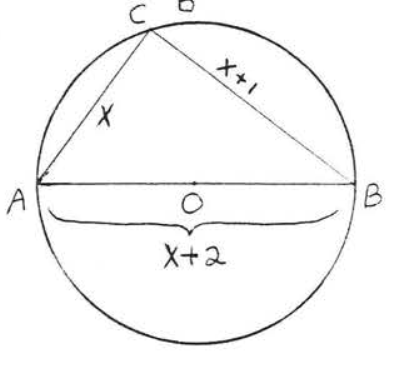
7 - 10. Find the area of the circle with... (use \(\pi = 3.14\))
7. radius 20.
8. radius 2.5.
9. diameter 12.
10. diameter 15.
11 - 14. Find the shaded area (use \(\pi = 3.14\)):
11.
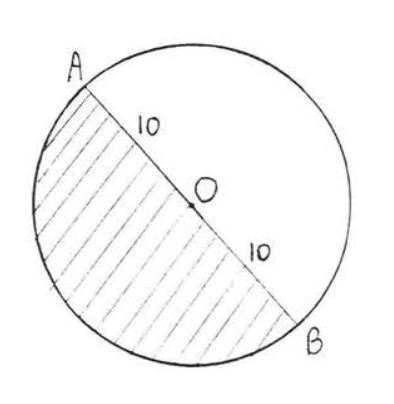
12.
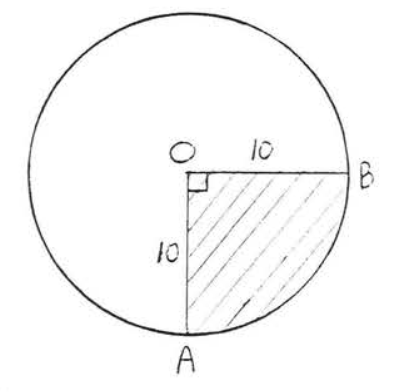
13.
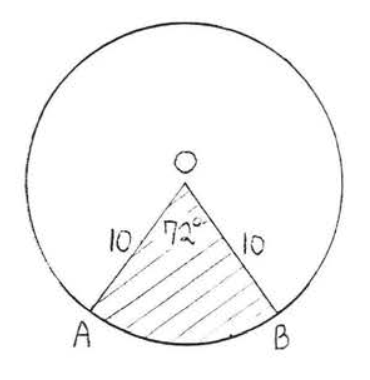
14.
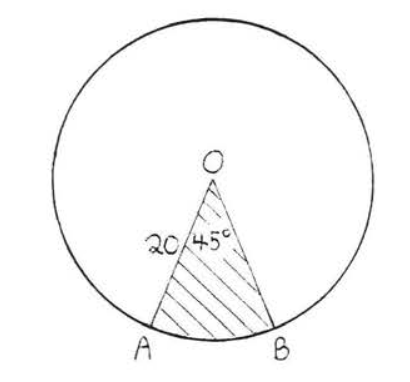
15 - 30. Find the shaded area. Answers may be left in terms of \(\pi\) and in radical form.
15.
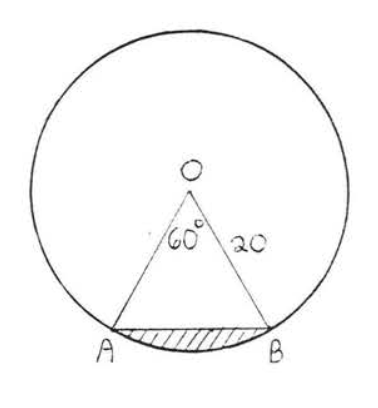
16.
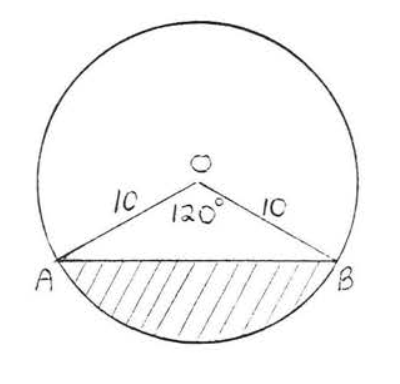
17.
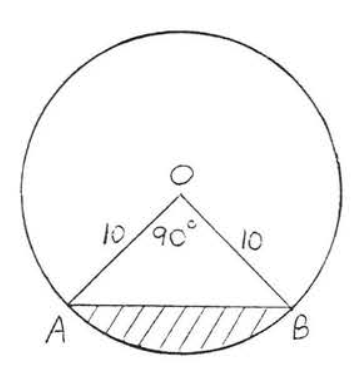
18.

19.
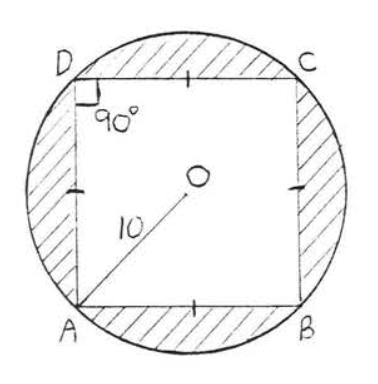
20.
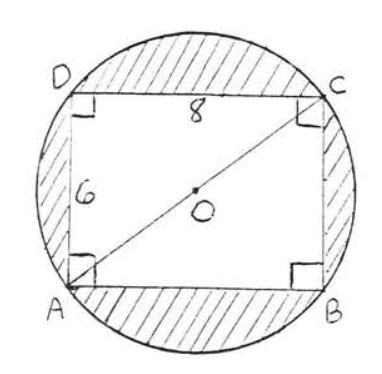
21.
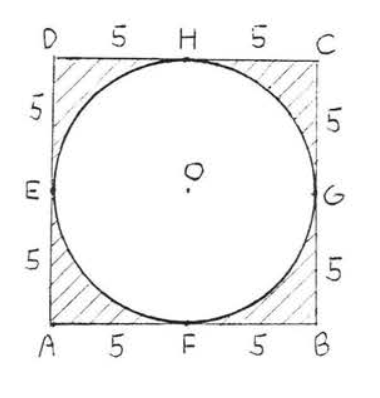
22.
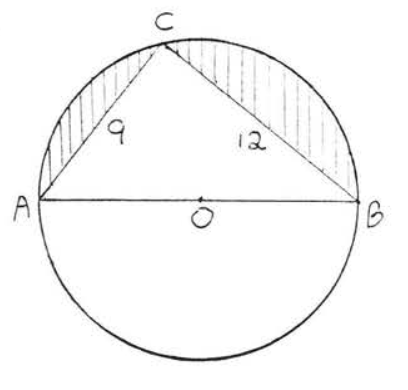
23.
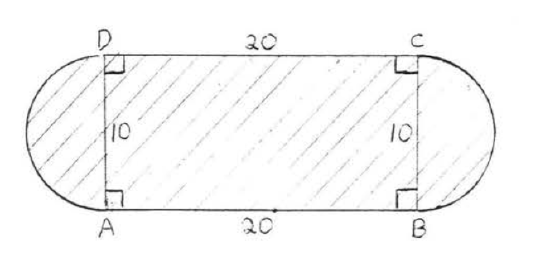
24.
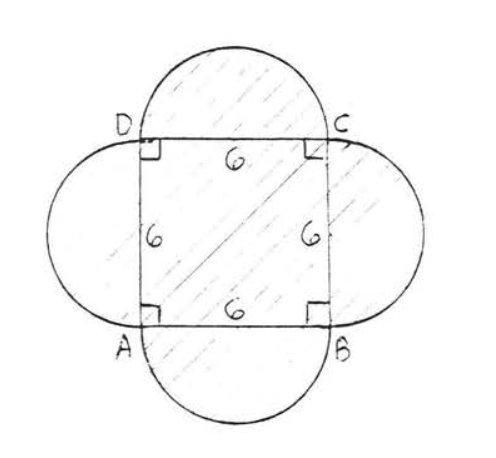
25.
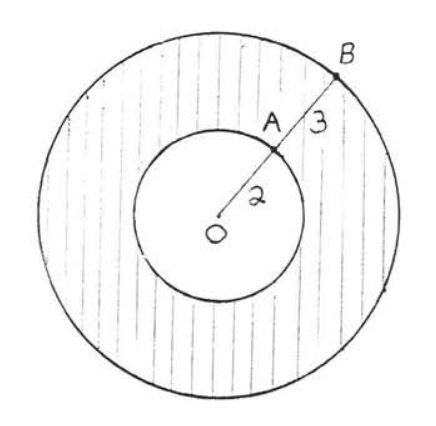
26.
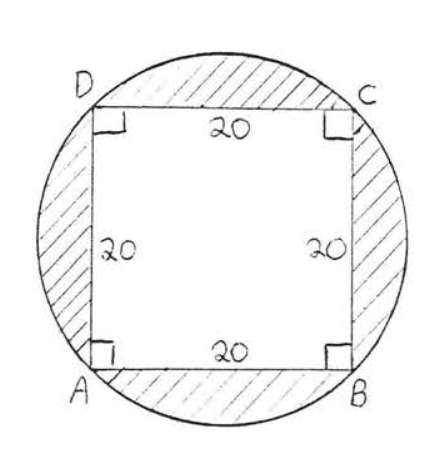
27.
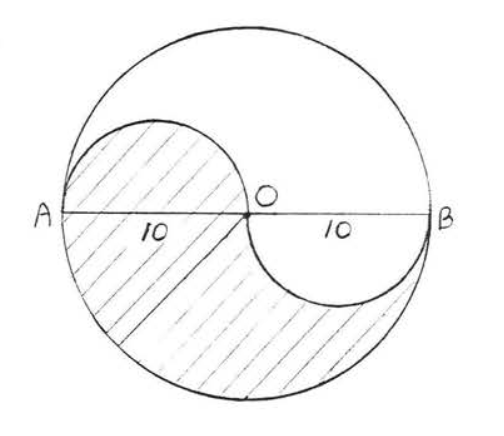
28.
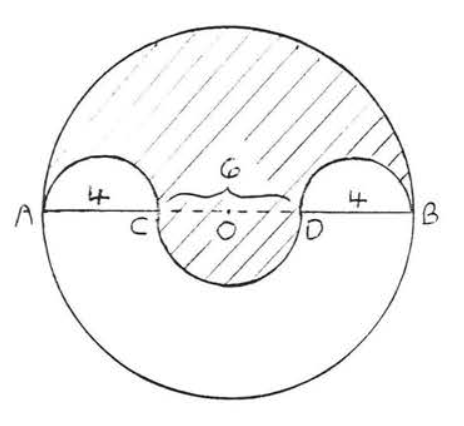
29.
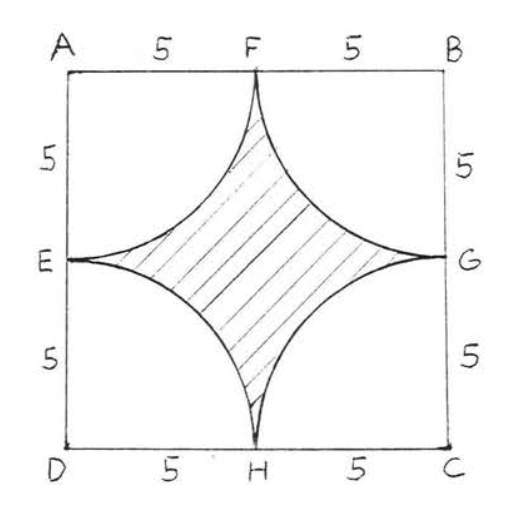
30.