12.9: Hyperbolic trigonometry
- Page ID
- 58346
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this section we give formulas for h-distance using hyperbolic functions. One of these formulas will be used in the proof of the hyperbolic Pythagorean theorem (Theorem 13.6.1).
Recall that \(\cosh\), \(\sinh\), and \(\tanh\) denote hyperbolic cosine, hyperbolic sine, and hyperbolic tangent; that is, the functions defined by
\(\cosh x := \dfrac{e^x + e^{-x}}{2}\), \(\sinh x := \dfrac{e^x - e^{-x}}{2}\),
\(\tanh x := \dfrac{\sinh x}{\cosh x}.\)
These hyperbolic functions are analogous to sine and cosine and tangent.
Prove the following identities:
\(\cosh' x=\sinh x\); \(\sinh'x=\cosh x\); \((\cosh x)^2-(\sinh x)^2=1.\)
The identities
\(\cosh (2 \cdot x) = (\cosh x)^2 + (\sinh x)^2\) and \(\sinh (2 \cdot x) = 2 \cdot \sinh x \cdot \cosh x\)
hold for any real value \(x\).
- Proof
-
\(\begin{array} {rcl} {(\sinh x)^2 + (\cosh x)^2} & = & {(\dfrac{e^x - e^{-x}}{2})^2 + (\dfrac{e^x + e^{-x}}{2})^2 =} \\ {} & = & {\dfrac{e^{2 \cdot x} + e^{-2 \cdot x}}{2} =} \\ {} & = & {\cosh (2 \cdot x);} \end{array}\)
\(\begin{array} {rcl} {2 \cdot \sinh x \cdot cosh x} & = & {2 \cdot (\dfrac{e^x - e^{-x}}{2}) \cdot (\dfrac{e^x + e^{-x}}{2})} \\ {} & = & {\dfrac{e^{2 \cdot x} - e^{-2 \cdot x}}{2}} \\ {} & = & {\cosh (2 \cdot x).} \end{array}\)
Let \(P\) and \(Q\) be two h-poins distinct from the center of absolute. Denote by \(P'\) and \(Q'\) the inverses of \(P\) and \(Q\) in the absolute.
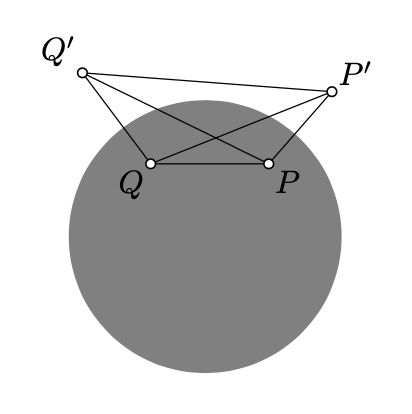
(a) \(\cosh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ' \cdot P'Q}{PP' \cdot QQ'}};\)
(b) \(\sinh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ \cdot P'Q'}{PP' \cdot QQ'}};\)
(c) \(\tanh [\dfrac{1}{2} \cdot PQ_h] = \sqrt{\dfrac{PQ \cdot P'Q'}{PQ' \cdot P'Q}};\)
(d) \(\cosh PQ_h = \dfrac{PQ \cdot P'Q' + PQ' \cdot P'Q}{PP' \cdot QQ'}\).
- Hint
-
By Corollary 10.6.1 and Theorem 10.2.1, the right hand sides in the identities survive under an inversion in a circle perpendicular to the absolute.
As usual we assume that the absolute is a unit circle. Suppose that \(O\) denotes the h-midpoint of \([PQ]_h\). By the main observation (Theorem 12.3.1) we can assume that \(O\) is the center of the absolute. In this case \(O\) is also the Euclidean midpoint of \([P Q]\). (Instead, we may move \(Q\) to the center of absolute. In this case the derivations are simpler. But since \(Q'Q = Q'P = QP = \infty\), one has to justify that \(\dfrac{\infty}{\infty} = 1\) every time.)
Set \(a = OP = OQ\); in this case we have
\(\begin{array} {rcl} {PQ} & = & {2 \cdot a,} \\ {P'Q'} & = & {2 \cdot \dfrac{1}{a},} \end{array}\) \(\begin{array} {l} {PP' = QQ' = \dfrac{1}{a} - a,} \\ {PQ' = QP' = \dfrac{1}{a} + a.} \end{array}\)
and
\(PQ_h = \ln \dfrac{(1 + a)^2}{(1 - a)^2} = 2 \cdot \ln \dfrac{1 + a}{1 - a}.\)
Therefore
\(\begin{array} {rcl} {\cosh [\dfrac{1}{2} \cdot PQ_h]} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + a}{1 - a} + \dfrac{1 - a}{1 + a})=} \\ {} & = & {\dfrac{1 + a^2}{1 - a^2};} \end{array}\) \(\begin{array} {rcl} {\sqrt{\dfrac{PQ' \cdot P'Q}{PP' \cdot QQ'}}} & = & {\dfrac{\dfrac{1}{a} + a}{\dfrac{1}{a} - a} =} \\ {} & = & {\dfrac{1 + a^2}{1 - a^2}.} \end{array}\)
Hence the part (a) follows. Similarly,
\(\begin{array} {rcl} {\sinh [\dfrac{1}{2} \cdot PQ_h]} & = & {\dfrac{1}{2} \cdot (\dfrac{1 + a}{1 - a} - \dfrac{1 - a}{1 + a}) =} \\ {} & = & {\dfrac{2 \cdot a}{1 - a^2};} \end{array}\) \(\begin{array} {rcl} {\sqrt{\dfrac{PQ \cdot P'Q'}{PP' \cdot QQ'}}} & = & {\dfrac{2}{\dfrac{1}{a} - a} =} \\ {} & = & {\dfrac{2 \cdot a}{1 - a^2}.} \end{array}\)
Hence the part (b) follows.
The parts (c) and (d) follow from (a), (b), the definition of hyperbolic tangent, and the double-argument identity for hyperbolic cosine, see Theorem \(\PageIndex{1}\).